Гипотеза Римана это математическая гипотеза, выведенная в 1859 году Бернхардом Риманом. И которая до сих пор не была решена.
Гипотеза Римана звучит так:
Если Гипотеза Римана верна, то
π(x) = Li(x) + Ο(√x∙ln x)
Гипотеза Римана имеет большое значение в квантовой механике, а также в криптографии.
В данном разделе я представлю две формулы с помощью которых я доказал Гипотезу Римана. Это новая формула функции π(x) и новый метод интегрирования функции 1/ln(x).
Функция π(x) показывает сколько в данном числе x простых чисел. Простые числа — это числа, которые делятся только на себя и на единицу. Например: 2 3 5 7…
Формула функции π(x).:
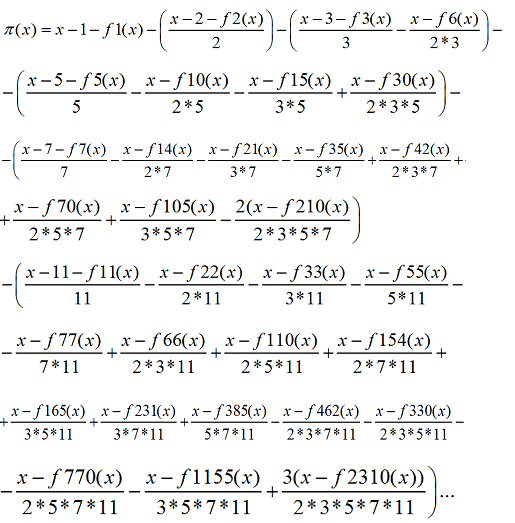
(1.1)
Доказательство:
Эта формула исключает из данного числа x все не простые числа, по правилам решета Эратосфена. Решето Эретосфена это метод, придуманный Эратосфеном Киренским для определения последовательности простых чисел. Алгоритм таков, если взять ряд из натуральных чисел без единицы
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18…
и исключить из него все четные числа, кроме самой маленькой из них, т.е. двойки, получится:
2 3 5 7 9 11 13 15 17…
А потом из этой получившейся последовательности исключить все числа которые делятся на следующее простое число после двойки, это число 3, не считая ее самой. Получится:
2 3 5 7 11 13 17…
Если так делать до бесконечности, то останутся только простые числа. Моя формула работает по такому принципу. Сначала формула исключает единицу из данного числа x, а потом количество всех четных чисел, кроме 2. Далее количество чисел, которые делятся на 3, кроме тройки, а из данного количества исключаются четные числа, которые которые делятся на 3 и т.д.
fn(x) обозначает самое минимальное число, которое надо исключить из x, чтобы получилось то число которое делится на n без остатка.
График функции fn(x):

Рис.(1.1) График функции fn(x)
Область определения функции

Область значения

Каждое выражение в скобках содержит количество определенных не простых чисел не превосходящих x.
Рано или позно определенное выражение в скобках формулы π(x) будет равна нулю (1.1). Поэтому данная сумма не бесконечна.
Я не могу доказать математически формулу (1.1), но можно понять, что формула верна, исходя из того что ее функция напоминает решето Эретосфена. Можно сказать, что эта формула-аналитический вариант решета Эретосфена.
Формула функции Li(x):
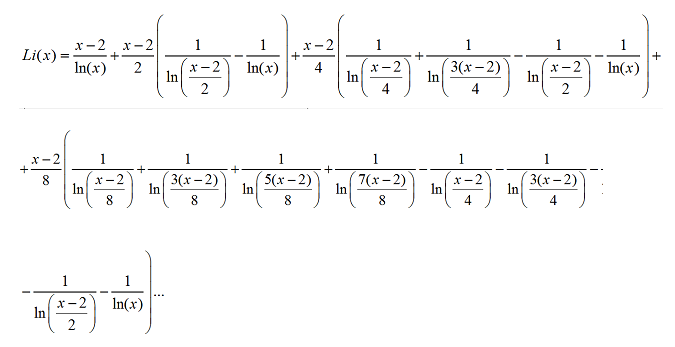
(1.2)
Доказательство:
Все члены этой суммы это площадь прямоугольника под графиком функции 1/ln(x), бесконечное количество площадей прямоугольников сходятся к площади под графиком функции 1/ln(x), начиная с аргумента 2. А так как функция Li(x) это интеграл графика функции 1/ln(x), то формула (1.2) равна Li(x).
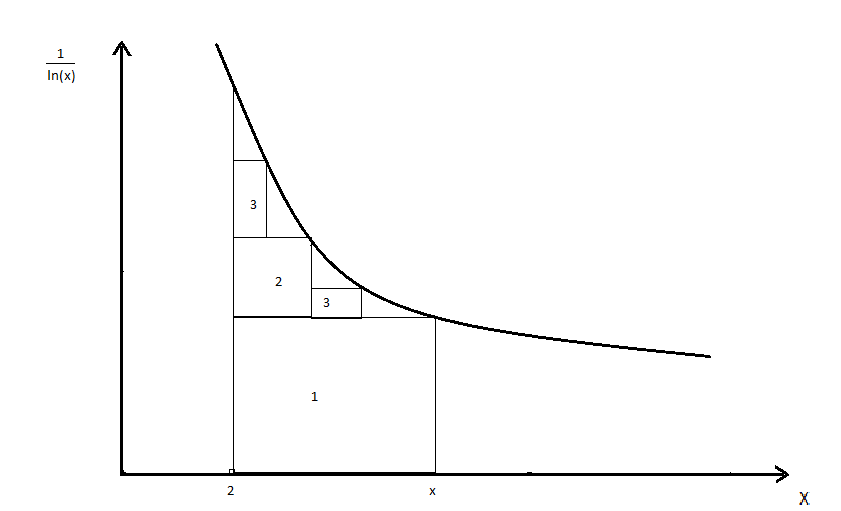
Рис.(1.2) Прямоугольники под графиком функции 1/ln(x)
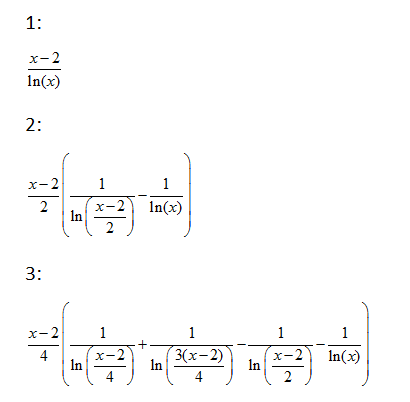
Верхний правый угол всех прямоугольников лежат на определенной точке графика, а так как прямоугольников бесконечно много, то углы прямоугольников охватывают все точки графика от 1/ln(2) до 1/ln(x).
Итак, если Гипотеза Римана верна то
π(x) = Li(x) + Ο(√x∙ln x)
А если переделать это выражение то получится, что
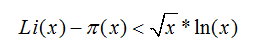
То есть, если доказать это неравенство то получится что Гипотеза Римана верна.
Подставив подставив выведенные формулы в неравенство получим:
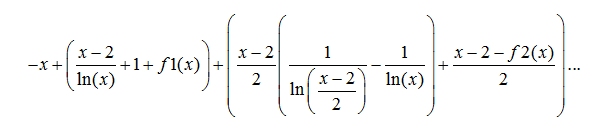
(1.3) Остаточный член
То есть
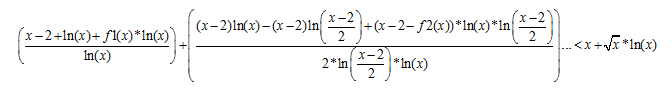
(1.4)
При условии что x>2.Преобразуем это выражение, для упрощения.
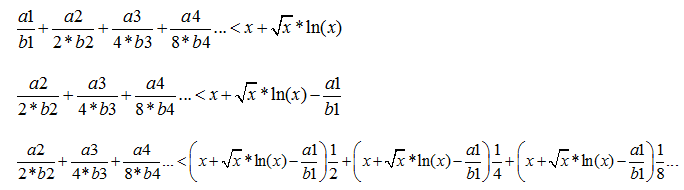
Из этого можно сделать вывод что, если неравенство

(1.5)
верное, то и Гипотеза Римана верна. Проверем это. Если перенести все члены неравенства (1.5) в правую часть неравенства, то получится

(1.6)
Первая разность этого выражения, при x>2, всегда отрицательна. А вторая разность отрицательна приблизительно лишь при x>10, но это не страшно, так как нас интересуют только большие аргументы, выражение (1.6) все равно будет верное.
Неравенство (1.6) верное, значит и неравенство
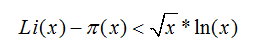
тоже верное.
Гипотеза Римана доказана.
Гипотеза Римана звучит так:
Все нетривиальные нули дзета-функции имеют действительную часть равную 1/2.Мне удалось доказать это утверждение. Мои выводы основываются на резултате фон Коха 1901 года.
Если Гипотеза Римана верна, то
π(x) = Li(x) + Ο(√x∙ln x)
Гипотеза Римана имеет большое значение в квантовой механике, а также в криптографии.
Формула π(x) и Li(x)
В данном разделе я представлю две формулы с помощью которых я доказал Гипотезу Римана. Это новая формула функции π(x) и новый метод интегрирования функции 1/ln(x).
Функция π(x) показывает сколько в данном числе x простых чисел. Простые числа — это числа, которые делятся только на себя и на единицу. Например: 2 3 5 7…
Формула функции π(x).:
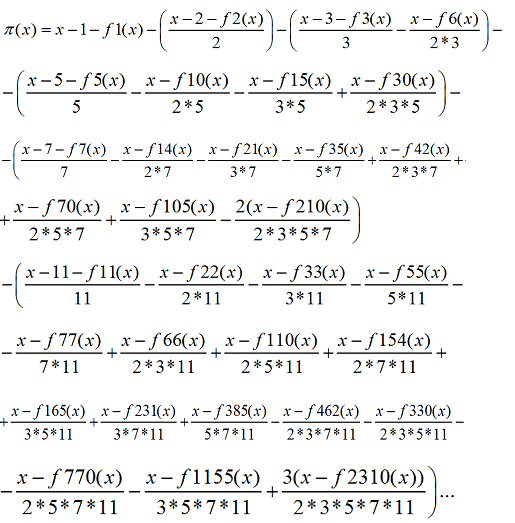
(1.1)
Доказательство:
Эта формула исключает из данного числа x все не простые числа, по правилам решета Эратосфена. Решето Эретосфена это метод, придуманный Эратосфеном Киренским для определения последовательности простых чисел. Алгоритм таков, если взять ряд из натуральных чисел без единицы
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18…
и исключить из него все четные числа, кроме самой маленькой из них, т.е. двойки, получится:
2 3 5 7 9 11 13 15 17…
А потом из этой получившейся последовательности исключить все числа которые делятся на следующее простое число после двойки, это число 3, не считая ее самой. Получится:
2 3 5 7 11 13 17…
Если так делать до бесконечности, то останутся только простые числа. Моя формула работает по такому принципу. Сначала формула исключает единицу из данного числа x, а потом количество всех четных чисел, кроме 2. Далее количество чисел, которые делятся на 3, кроме тройки, а из данного количества исключаются четные числа, которые которые делятся на 3 и т.д.
fn(x) обозначает самое минимальное число, которое надо исключить из x, чтобы получилось то число которое делится на n без остатка.
График функции fn(x):

Рис.(1.1) График функции fn(x)
Область определения функции

Область значения

Каждое выражение в скобках содержит количество определенных не простых чисел не превосходящих x.
Рано или позно определенное выражение в скобках формулы π(x) будет равна нулю (1.1). Поэтому данная сумма не бесконечна.
Я не могу доказать математически формулу (1.1), но можно понять, что формула верна, исходя из того что ее функция напоминает решето Эретосфена. Можно сказать, что эта формула-аналитический вариант решета Эретосфена.
Формула функции Li(x):
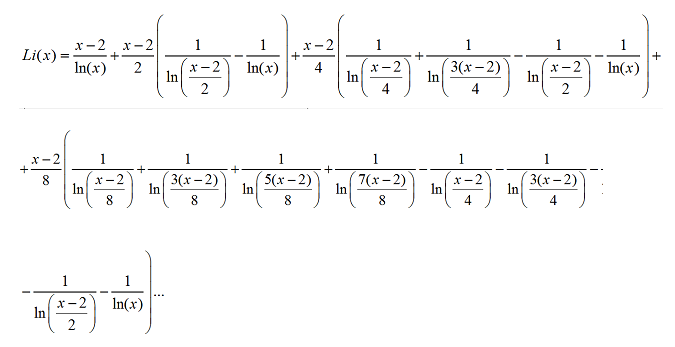
(1.2)
Доказательство:
Все члены этой суммы это площадь прямоугольника под графиком функции 1/ln(x), бесконечное количество площадей прямоугольников сходятся к площади под графиком функции 1/ln(x), начиная с аргумента 2. А так как функция Li(x) это интеграл графика функции 1/ln(x), то формула (1.2) равна Li(x).

Рис.(1.2) Прямоугольники под графиком функции 1/ln(x)
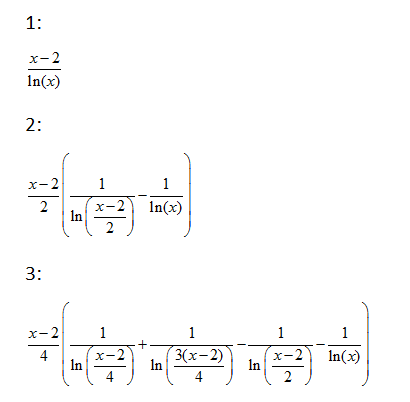
Верхний правый угол всех прямоугольников лежат на определенной точке графика, а так как прямоугольников бесконечно много, то углы прямоугольников охватывают все точки графика от 1/ln(2) до 1/ln(x).
Доказательство
Итак, если Гипотеза Римана верна то
π(x) = Li(x) + Ο(√x∙ln x)
А если переделать это выражение то получится, что
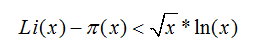
То есть, если доказать это неравенство то получится что Гипотеза Римана верна.
Подставив подставив выведенные формулы в неравенство получим:
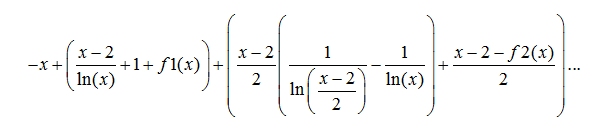
(1.3) Остаточный член
То есть
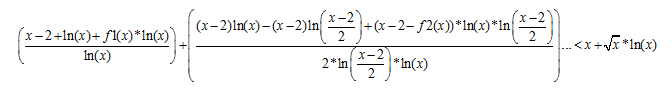
(1.4)
При условии что x>2.Преобразуем это выражение, для упрощения.
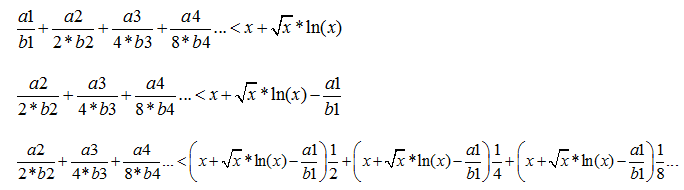
Из этого можно сделать вывод что, если неравенство

(1.5)
верное, то и Гипотеза Римана верна. Проверем это. Если перенести все члены неравенства (1.5) в правую часть неравенства, то получится

(1.6)
Первая разность этого выражения, при x>2, всегда отрицательна. А вторая разность отрицательна приблизительно лишь при x>10, но это не страшно, так как нас интересуют только большие аргументы, выражение (1.6) все равно будет верное.
Неравенство (1.6) верное, значит и неравенство
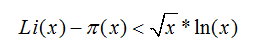
тоже верное.
Гипотеза Римана доказана.