Мы продолжаем рассказывать о системе адаптивного обучения на Stepic.org. Первую вводную часть этой серии можно почитать здесь.
В данной статье мы расскажем о построении рекомендательной системы (которая и лежит в основе адаптивности). Расскажем о сборе и обработке пользовательских данных, о графах переходов, хендлерах, оценке реакции пользователя, формировании выдачи.
Вспомним про линейную регрессию, регуляризацию и даже поймём, почему в нашем случае лучше использовать гребневую регрессию, а не какую-нибудь там ещё.
Общие слова
Рекомендательная система на Stepic.org предлагает пользователю новые уроки (образовательный контент) на основании того, чем он интересовался ранее. Она использует для этого различные способы найти контент, чем-то похожий на тот, который пользователь уже изучал, или же не столь похожий, но в целом интересный.
Каждый из таких способов оформлен в виде отдельной функции (хендлера), которая извлекает список уроков по заложенному в нему принципу и размечает их весами в зависимости от того, насколько они подходят пользователю. Подробное описание этих функций-хендлеров будет ниже.
Рекомендательная система может применяться в разных ситуациях. Два основных случая:
- обычная рекомендация для конкретного пользователя, которая показывается ему на главной странице и во вкладке ”Рекомендованные уроки”, а также время от времени присылается на почту;
- контекстная рекомендация, которая показывается пользователю после прохождения урока вне курса (то есть урока, для которого нет фиксированного следующего за ним), как подсказка, что посмотреть дальше.
Вместе с рекомендацией пользователю также показывается информация о том, почему ему был предложен именно этот урок. Эту информацию легко извлечь благодаря тому, что в каждую функцию-хендлер заложена какая-то интуиция, так что можно восстановить причину рекомендации.
Пользовательские данные
В процессе обучения на Stepic.org пользователь оставляет значительный цифровой след. Помимо информации о его прогрессе сохраняются также сведения о том, когда он посещал разные шаги (шаг — элементарная единица контента; шаги объединяются в более крупные уроки), когда пытался решать задачи и с каким результатом, и даже как он смотрел видео: какие установил скорость и громкость, где останавливал и где перематывал.
Наиболее интересны для базовой рекомендательной системы следующие сведения: теги (т.е. области знаний, которыми протегированы уроки), которыми пользователь интересовался, уроки, на которые он заходил, уроки, которые он изучил, а также, если рекомендация контекстная, текущий урок.
Кроме информации о конкретном пользователе, сохраненные данные можно рассматривать как сведения о взаимодействии пользователей с контентом. Одним из способов агрегировать и использовать эти сведения оказались графы переходов, о которых расскажем подробнее.
Графы переходов
Часто бывает полезно узнать, как пользователи изучают контент, что они смотрят чаще, что реже, какие материалы проскакивают, на какие возвращаются, и, что немаловажно, в каком порядке их смотрят. Используя логи о действиях пользователей, несложно дать ответы на эти вопросы. Мы использовали для этого граф переходов (process map), то есть такой ориентированный граф, в котором вершинами будут единицы контента (например, шаги или уроки), а веса дуг будут показывать количество переходов между этими единицами контента.
У каждого пользовательского действия в логе есть временна́я метка. Действия также бывают разных типов, например, "viewed" (открыл шаг), "succeeded attempt" (решил задачу) или "commented" (оставил комментарий). Нас будут интересовать действия пользователя по отношению к шагам, которые затем легко обобщить на уроки, к которым эти шаги принадлежат, и даже на теги, которыми помечены уроки.
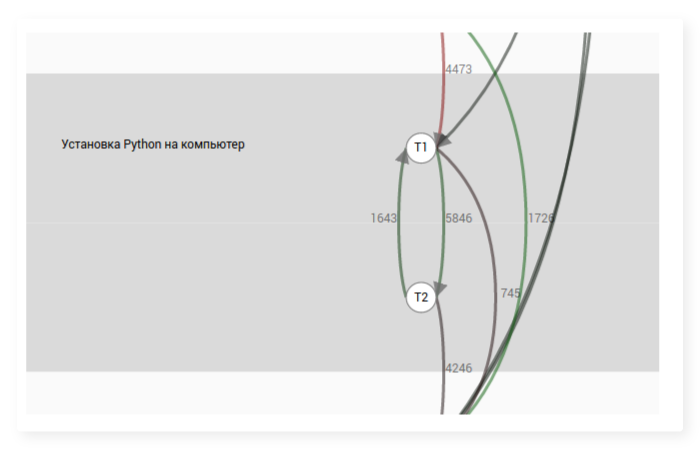
Визуально граф переходов можно представить себе как ряд вершин-материалов (например, шагов), между некоторыми из которых есть дуги. Наличие дуги между двумя шагами означает, что существуют пользователи, которые просмотрели их друг за другом. Каждая дуга обладает меткой, содержащей число таких пользователей. Пример графа переходов для шагов одного урока внутри курса:
Процесс построения графа переходов тривиален: для каждого пользователя мы рассматриваем все его действия по отношению к шагам, сортируем их по времени, и затем подсчитываем для каждой пары шагов, сколько раз он совершал действие с одним из них непосредственно после действия с другим. Далее мы суммируем частоты для всех пользователей, и получается общий граф переходов.
Изначально мы ввели графы переходов по шагам, чтобы преподаватели могли узнать, в каком порядке учащиеся изучают материалы их курсов. Для простоты анализа мы вычисляем среднюю частоту переходов между шагами в курсе и окрашиваем ребра в итоговом графе зеленым, если переход по ним происходил чаще ожидаемого, или красным, если реже ожидаемого, а также выкидываем редкие переходы.
Фрагмент графа переходов по одному из курсов:
По этому фрагменту видно, что шаг с теорией Т4 пропускают чаще обычного и переходят к следующему за ним.
Далее мы стали строить графы переходов не только по шагам, но также по урокам и тегам, чтобы использовать это в рекомендательной системе. Граф переходов по урокам строится по тому же принципу, что и для шагов, просто действия над шагами рассматриваются как действия над уроками, к которым эти шаги принадлежат. Для тегов процесс аналогичен: действия с шагами переводятся в действия с их тегами.
Хендлеры
Здесь мы перечислим функции-хендлеры, каждая из которых реализует свой способ рекомендаций. Хендлер принимает в качестве параметров пользователя, и, если рекомендация контекстная, то урок, на котором пользователь находится в данный момент. Хендлер возвращает для пользователя список уроков, каждому из которых соответствует вес от 0 до 1. Чем больше вес, тем лучше рекомендация:
.
Пусть мы хотим порекомендовать пользователю уроки по конкретному тегу, для которого доля пройденных пользователем уроков составляет
. В случае, если по нему нет графа переходов, все его уроки получают вес
. Если же граф есть, то для каждого урока этот вес делится на расстояние в графе до ближайшего предшествующего урока, пройденного пользователем
. Таким образом реализуется идея, что пользователю может быть интересно проходить материалы, расположенные в графе переходов недалеко от уже изученных им.
Уроки с интересными пользователю тегами — хендлер рекомендует уроки, помеченные тегами, которые пользователь уже изучал. Для этого используется описанная выше рекомендация по тегам, вес урока
для пользователя
будет составлять
.
Незаконченные уроки — рекомендуются уроки, которые пользователь начинал и не закончил, с весом тем большим, чем большую часть урока пользователь изучил:
, доля урока
Популярные уроки — хендлер не использует информацию о пользователе, а рекомендует просто самые популярные за последнюю неделю уроки на платформе. Вес прямо пропорционален популярности:
, где
— номер урока
Пути по урокам — используются пути, содержащие уроки, которые пользователь проходил, рекомендуются уроки следом за пройденными, с весом тем меньшим, чем дальше урок от уже пройденных:
, где
— расстояние от урока
Граф переходов по тегам — рекомендуются уроки с тегами, которые изучают после тегов, интересующих пользователя. Веса зависят от прогресса пользователя по тегам, а также от относительных частот переходов между тегами. Пусть
— частота перехода от тега, уроки которого пользователь изучал, к некоторому тегу
. Тогда для урока
.
Уроки по тегам от похожих пользователей (коллаборативная фильтрация) — на основе интересующих пользователя тегов выявляются пользователи с похожими на его интересами, и рекомендуются уроки с тегами, которые они сами изучают. Пусть у текущего пользователя
, причем мера схожести между ними —
(лежит между 0 и 1, чем она больше, тем более схожи пользователи). Тогда урок
.
Граф переходов по урокам (только при контекстных рекомендациях) — хендлер рекомендует уроки, следующие за текущим в графе переходов, вес зависит от относительной частоты перехода между текущим уроком и рекомендуемым. Если переход из текущего урока в урок
, то
.
- Пути по урокам (только при контекстных рекомендациях) — рекомендуются уроки, следующие за текущим в каких-либо путях, веса обратно пропорциональны расстоянию между уроками:
, где
— расстояние от урока
- Если все предыдущие хендлеры в совокупности порекомендовали меньше уроков, чем было нужно, в рекомендации добавляются случайные уроки, вес таких уроков равняется 0.
Разобрались? Отлично, идём дальше.
Оценка реакции пользователя
Чтобы понять, насколько успешна оказалась рекомендация, после её показа мы фиксируем, перешёл ли пользователь по ссылке, а также какую часть от урока пользователь в итоге изучил (значение от 0 до 1). В то же время у пользователя есть возможность узнать, почему урок был посоветован (варианты соответствуют хендлерам), и пометить рекомендацию как не интересную ему.
В результате каждой показанной рекомендации мы можем сопоставить некоторое число: соответствует отказу от рекомендаций,
— переходу по ссылке без изучения урока,
— переходу по ссылке и полному изучению урока, значение от
до
— неполному изучению урока, а
— отсутствию реакции.
Формирование выдачи
Итак, мы получили списки уроков от нескольких хендлеров, в которых каждому уроку сопоставлен вес от 0 до 1. Чем больше, тем более удачной оценивает хендлер эту рекомендацию. Встает вопрос, как их лучше всего комбинировать?
Можно было бы просто для каждого урока сложить или перемножить веса хендлеров, которые его посоветовали. Но это означало бы, что мы полагаем разные хендлеры одинаково полезными, что, вообще говоря, может быть совсем не так. Хотелось бы оценить каждый хендлер коэффициентом полезности, используя при этом реакции пользователей на рекомендации. Таким требованиям удовлетворяет простая линейная регрессия.
Регрессионная модель обучается с использованием накопленных данных о том, как рекомендации разных хендлеров были оценены пользователем. Исходя из этого модель формирует вектор весов для хендлеров. Далее, когда нам нужна что-то порекомендовать учащемуся, то регрессионная модель для каждого урока скалярно умножает веса предложивших его хендлеров с обученным вектором параметров, и выдает результирующий вес для каждого рекомендованного урока.
Раз уж мы так углубились в матчасть, то давайте формально опишем регрессионную модель. Если вы хорошо знаете, что такое линейная регрессия, то смело пропускайте следующий раздел.
Линейная регрессия
Пусть у нас есть матрица , строки которой
называются наблюдениями, а столбцы факторами, и столбец значений целевой или зависимой переменной
. Регрессионная модель
, где
— параметры модели, а
— случайная ошибка, называется линейной, если зависимость целевой переменной от факторов является линейной, то есть
.
Обычно для удобства (константу) вносят под знак суммы, добавив в матрицу наблюдений столбец из единиц:
для всех
.
Используя эти обозначения, линейную регрессионную модель можно выписать как . Решением этой задачи будем считать столбец
, который минимизирует сумму квадратов отклонений предсказываемых значений от реальных, то есть
.
Такой способ аппроксимации называется методом наименьших квадратов (ordinary least squares) и является наиболее широко применимым в контексте решения задачи линейной регрессии.
В нашем случае мы можем рассматривать в качестве наблюдений, то есть строк матрицы , рекомендованные уроки, в качестве факторов этих наблюдений веса, которые хендлеры назначили уроку, а в качестве значений целевой переменной — оценку рекомендации пользователем.
Таким образом, для уроков , посоветованных пользователям
соответственно, и для хендлеров
матрица наблюдений
и столбец значений целевой переменной (реакции пользователя)
будут выглядеть следующим образом:
Вектор , который дает минимальную ошибку предсказания реакции пользователя, содержит индивидуальный вес для каждого из хендлеров, на который нужно домножать его рекомендации. Если вес какого-то из хендлеров относительно большой, значит, этот хендлер вносит положительный вклад в рекомендации, и наоборот.
Для работы рекомендательной системы регрессионная модель регулярно переобучается на данных о реакции пользователей на рекомендации. Мы используем библиотеку SciPy для решения этой задачи и нахождения столбца . В этой библиотеке уже реализовано решение задачи линейной регрессии.
Разобрались? Отлично, осталось чуть-чуть.
Регуляризация
После реализации рекомендательной системы с линейной регрессией, которая находила столбец весов для хендлеров , минимизирующий квадрат отклонений реальной реакции пользователя от предсказанной (
), мы заметили, что постепенно вес одного хендлера неограниченно возрастает, в то время как остальные уменьшаются, что в итоге привело к формированию выдачи практически только из результатов этого хендлера. Такой эффект называется положительной обратной связью, и характеризуется тем, что отклонение в результатах работы системы влияет на её дальнейшую работу, причем чем дальше, тем больше результаты сдвигаются в сторону этого отклонения.
Помимо этого, так как хендлеры могут использовать очень схожую информацию об активности пользователя, в наших данных также может присутствовать проблема мультиколлинеарности факторов, что влечет за собой слабую обособленность матрицы и, как следствие, нестабильность решения.
В результате мы получаем решение, которое дает маленькую ошибку на данных, на которых оно обучается, и большую на реальных данных. Эта ситуация называется переобучением (overfitting) модели.
В качестве решения проблемы переобучения можно рассмотреть регуляризацию. Согласно книге The Elements of Statistical Learning, основные способы регуляризации — это лассо (LASSO, least absolute shrinkage and selection operator) и гребневая регрессия (резуляризация Тихонова, ridge regression). Оба этих метода меняют выражение, которое мы минимизируем в процессе поиска решения регрессии, добавляя к нему штраф на норму вектора .
В случае лассо-регуляризации используется -норма и решение находится как
В случае же гребневой регрессии используется -норма и решение выглядит как
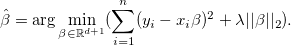
В обоих случаях параметр подбирается в процессе оптимизации.
Использование регуляризации методом лассо уменьшает все веса , а те, что и так были относительно небольшими, становятся равны нулю. Таким образом, метод лассо хорошо подходит для выбора значащих факторов (feature selection).
Метод гребневой регрессии также уменьшает веса факторов, но при этом никогда не сводит их к нулю, если только не .
Согласно работе Andrew Ng, лассо-регуляризация работает лучше гребневой в ситуации, когда количество факторов значительно превосходит число обучающих наблюдений. В обратной же ситуации более уместна гребневая регрессия.
Соответственно, для нашего случая лучше подходит гребневая регрессия. Её реализация также присутствует в библиотеке SciPy, что нас очень порадовало.
Заключение
В этой статье мы с вами разобрались с тем, как реализована рекомендательная система для образовательного контента на Stepic.org. Иногда, наверное, приходилось нелегко, но вам удалось! (если вы, конечно, не просто прокрутили до этого места, тогда советуем вернуться и прочитать)
Посмотреть рекомендательную систему в действии можно на https://stepic.org/explore/lessons – там перечислены рекомендованные вам уроки для изучения. Но если вы впервые зашли на платформу, то рекомендации могут быть не особо релевантны.
В следующей и заключительной статье этого цикла мы рассмотрим непосредственно адаптивную систему на Стэпике и обсудим результаты проделанной работы: точность предсказания, предпочтения пользователей, оценим статистику.
И напоследок хочется спросить: верите ли вы в адаптивное онлайн-образование? Вытеснит ли оно традиционные курсы? Может ли самая интеллектуальная рекомендательная система посоветовать человеку образовательный контент так же хорошо и даже лучше, чем живой преподаватель?
