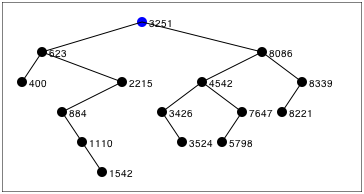
Когда я начал изучать ruby, я решил реализовать бинарное дерево и некоторые из его основных операций (insert, delete, walk, и search), для того, что бы лучше вникнуть в язык. Бинарные деревья, это хорошее упражнение, что бы понять особенности языка, такие как: условные операторы, циклы, классы. В то же время, это возможность решить интересную задачу. Алгоритм бинарного дерева хорошо описан во многих книгах и в интернете.Для усложнения задачи, я так же реализовал отрисовку бинарного дерева средствами html5 и Canvas. Это позволяет более наглядно понять работу бинарного дерева. Вы можете посмотреть демонстрацию на веб сайте.
Далее я кратко опишу реализацию основных методов построения бинарного дерева.
Бинарное дерево или дерево двоичного поиска
Собственно код, представленный ниже, реализует Дерево двоичного поиска (BST), которое является более конкретной версией бинарных деревьев. В двоичном дереве, каждый узел имеет не более 2 детей, один из них называется «левое поддерево», а другой «правое поддерево», сортировка отсутствует. В двоичном дереве поиска, все узлы хранятся в порядке, отраженном в следующем правиле:
Допустим x это узел в двоичном дереве поиска, если y является «левым поддеревом» для x, то y.key ≤ x.key. Если y является «правым поддеревом» для x, то y.key ≥ x.key.
Реализация бинарного дерева поиска
Класс, для работы с деревом, который я реализовал можно использовать следующим образом:
require "binarytree"
tree = BinaryTree.new(40)
tree.add(30)
tree.add(100)
tree.add(20)
tree.add(35)
tree.add(25)
tree.add(34)
puts "Tree nodes: #{tree.to_s}" => "20, 25, 30, 34, 35, 40, 100"Этот клас мы можем использовать с числами, строками или любыми собственными типами ruby, поддерживающими сопоставление (т.е. <=>)
Добавление узлов в бинарном дереве
Код для добавления узлов в бинарном дереве показан ниже. Этот код сначала проверяет, есть ли у нас уже корневой узел, если нет, то создаем корневой узел с новым значением. Если у нас уже есть корневой узел, сканируем узлы дерева (с помощью правила указанного выше) пока не дойдем до конеч��ого узла. Как только мы достигли конечного узла мы обновляем его, чтобы указать на новый узел.
def add(new_value)
if @root == nil
@root = Node.new(new_value)
@total_nodes = 1
return
end
current = @root
while(true)
if new_value >= current.value
if current.right == nil
current.right = Node.new(new_value)
break
else
current = current.right
end
else
if current.left == nil
current.left = Node.new(new_value)
break
else
current = current.left
end
end
end
@total_nodes += 1
end
Ходьба по дереву
Одним из преимуществ двоичного дерева поиска в том, что очень легко получить значения, хранящиеся в нем. Этот процесс называется «ходьба по отсортированному дереву». Например, если у нас есть дерево со следующими значениями: 100, 50, 200 и 150, то отсортированное дерево даст нам значения: 50, 100, 150 и 200. Хождение по дереву можно реализовать с помощью рекурсивной функции. Однако рекурсивный метод, хотя и элегантный, но не очень эффективен, если дерево большого размера. Код, который я реализовал не использует рекурсию, но вместо этого использует массив, как стек для отслеживания узлов, которые он посещает. Это решение не такое элегантное, как рекурсия, но оно хорошо работает, даже если в дереве тысячи узлов.
def walk
return nil if @root == nil
node = @root
stack = []
ignore_left = false
while(true)
#p "processing #{node.value.to_s}"
if ignore_left
#p "ignoring nodes to the left"
ignore_left = false
else
if node.left != nil
#p "moving to the left"
stack << node
node = node.left
next
end
end
yield node
if node.right != nil
#p "moving to the right"
node = node.right
next
end
break if stack.length == 0
#p "popping from the stack"
node = stack.pop
ignore_left = true
end
end
Пока я реализовывал этот метод, я понял красоту и простоту одной из самых лучших возможностей ruby: блоки. Когда алгоритм находит следующий узел для обработки, он просто отдает его вызывающей программе. Это позволяет ходить по дереву и быть полностью независимым от действий, которые мы хотим выполнить на каждом узле. Например вы можете сделать для каждого узла такой код:
tree.walk { |node| puts "#{node.value}" }
В этом примере блок просто «выводит» значения, но мы увидим, более сложный пример, когда рассмотрим код для отрисовки двоичного дерева.
Как рисовать Двоичное дерево
Алгоритм отрисовки двоичного дерева, в значительной степени похож, на алгоритма хождения по дереву с тем исключением, что нам нужно вычислить координаты, где каждый узел должен быть размещен и как мы пересекаем узлы. Расчет координат оказалась интересной задачей.
Основной алгоритм заключается в следующем:
- Нарисовать корневой узел с заданными координатами
- Нарисовать левое поддерево с лева от корневого узла
- Нарисовать правое поддерево с права от корневого узла
def draw_node(root, x, y, block)
return if root == nil
block.call(root, x, y, x, y)
draw_left(root.left, x, y, block) if root.left != nil
draw_right(root.right, x, y, block) if root.right != nil
end
Для вычисления координат левого поддерева, рассчитываем сколько детей с правой стороны левого поддерева. Полученное число, мы используем для отрицательного смещения по оси x. Дальше мы рекурсивно вызываем этот метод для левого и правого поддерева.
def draw_left(node, parent_x, parent_y, block)
if node.right != nil
count = 1 + children_count(node.right)
else
count = 0
end
x = parent_x - @x_distance - (count*@x_distance)
y = parent_y + @y_distance
block.call(node.value, x, y, parent_x, parent_y)
draw_left(node.left, x, y, block) if node.left != nil
draw_right(node.right, x, y, block) if node.right != nil
end
Для правого поддерева, делаем все тоже самое, но наоборот.
def draw_right(node, parent_x, parent_y, block)
if node.left != nil
count = 1 + children_count(node.left)
else
count = 0
end
x = parent_x + @x_distance + (count*@x_distance)
y = parent_y + @y_distance
block.call(node.value,x,y, parent_x, parent_y)
draw_left(node.left, x, y, block) if node.left != nil
draw_right(node.right, x, y, block) if node.right != nil
end
Как и метод walk, метода отрисовки по факту ничего не рисуют, а лишь указываю координаты отображения объекта. Следующий пример показывает построение дерева с координатами в консоли:
require "binarytree"
require "binarytreedrawer"
tree = BinaryTree.new
tree.add(100)
tree.add(50)
tree.add(150)
tree.add(25)
tree.add(75)
tree.add(125)
tree.add(175)
drawer = BinaryTreeDrawer.new(tree)
drawer.draw(0,0, Proc.new { |value, x, y, px, py|
puts "Value #{value} at (#{x}, #{y})"
})
=> Value 100 at (0, 0)
=> Value 50 at (-40, 30)
=> Value 25 at (-60, 60)
=> Value 75 at (-20, 60)
=> Value 150 at (40, 30)
=> Value 125 at (20, 60)
=> Value 175 at (60, 60)
Реальный пример отрисовки Бинарного дерева на веб-странице
Имея координаты мы можем использовать любую графическую программу для отрисовки дерева. В этом веб-приложение я буду использовать HTML 5 Сanvas как поверхность для рисования, и несколько JS методов. Ниже представлен простой пример, как я генерирую JS вызовы для отрисовки дерева:
drawer = BinaryTreeDrawer.new(@tree)
drawer.draw(0, 0, Proc.new { |value, x, y, px, py|
circles << "draw_circle(centerX + #{x}, offsetY + #{y}, 5);"
lines << "draw_line(centerX + #{x}, offsetY + #{y}, centerX + #{px}, offsetY + #{py});"
labels << "draw_label(centerX + 7 + #{x}, offsetY+5+#{y}, \"#{value}\");"
})
Обратите внимание, что этот код просто создает три массива (круги, линии, ярлыки) с вызовами JavaScript методов. Эти массивы позднее, вставляются в веб-страницу и рисуют дерево на стороне клиента.
Исходный код и Демонстрация
Если вы хотите увидеть демо, вы можете посетить http://binarytree.heroku.com и генерировать несколько бинарных деревьев со случайными данными или нарисовать двоичного дерево с собственным набором данных.
Все исходники, для реализации двоичного дерева, а также демо-сайт, выложены на GitHub.
