Comments 14
А потом удивляются, что студенты сложные темы не понимают :)
Применяю нечеткий вывод для расчета риска мошенничества и риска неплатежеспособности в потребительском кредитовании. Преимущества перед методами машинного обучения: использует знания экспертов, причем эти знания вводятся в систему в качественной форме правил типа «Если платежная дисциплина низкая, а срок просрочки небольшой, то риск мошенничества невысокий». Недостатки: слабые способности к обобщению, непокрытые правилами примеры не всегда корректно обрабатываются.
Спасибо за информацию из цитируемой книги, попробую формулы дефуззификации, испльзованные у вас. У меня до сих пор лучше всего работал простой минимакс. Правда, это следует из специфики задачи: много правил-признаков мошенничества, и если сработало хоть одно из них, риск уже должен считаться высоким.
Спасибо за информацию из цитируемой книги, попробую формулы дефуззификации, испльзованные у вас. У меня до сих пор лучше всего работал простой минимакс. Правда, это следует из специфики задачи: много правил-признаков мошенничества, и если сработало хоть одно из них, риск уже должен считаться высоким.
Java всё же не самый лучший язык для решения таких задач.
Мы решали такие задачи на прологе — гораздо удобнее, меньше кода.
Задав правила можно отвечать на вопросы с «обратной стороны».
Очень уже было элегантно и красиво.
Мы решали такие задачи на прологе — гораздо удобнее, меньше кода.
Задав правила можно отвечать на вопросы с «обратной стороны».
Очень уже было элегантно и красиво.
Ни в коем случае не против Java в целом. коментарий провокационный — интересует ваше мнение.
У меня было именно такое задание — реализовать данный метод на яве (на платформах SE и EE), а приказы не обсуждаются (:
Да, на осознание и полное перебивание алгоритма ушла куча времени, а чтобы не зашивать намертво этот самый пример, еще и пришлось расплодить кучу классов (функции, правила, их интерфейсы и класс ввода Input можно было засунуть в один, но тогда это была бы просто демка для конкретной задачи).
На прологе писать не доводилось и, честно, я его совсем не знаю — сравнить не могу. Покажете как решить эту задачу на нем — с удовольствием прочитаю и тогда можно будет сравнить (насколько слышал, пролог как раз заточен именно под логику и эта задача как раз для него).
Да, на осознание и полное перебивание алгоритма ушла куча времени, а чтобы не зашивать намертво этот самый пример, еще и пришлось расплодить кучу классов (функции, правила, их интерфейсы и класс ввода Input можно было засунуть в один, но тогда это была бы просто демка для конкретной задачи).
На прологе писать не доводилось и, честно, я его совсем не знаю — сравнить не могу. Покажете как решить эту задачу на нем — с удовольствием прочитаю и тогда можно будет сравнить (насколько слышал, пролог как раз заточен именно под логику и эта задача как раз для него).
У меня вопрос. Почему переменную Y задали на множестве J={0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1}?
Если именлся в виду весовой вектор X (его можно видеть над каждым столбцом матриц D), то он характеризует степень удовлетворительности, поэтому может принимать значения от 0 (не удовлетворяет) до 1 (удовлетворяет полностью). Т.к. в данном случае это дискретная величина, значения его элементов изменяются с некоторым фиксированным шагом, конкретно тут — 0.1 (для удобства и наглядности; его можно уменьшить для большей точности или увеличить для ускорения расчетов).
то есть мы так задали множество допустимых значений весового вектора и по нему ранжируем характеристики претендентов так? Мне просто не очень понятно откуда берутся такие значения в матрице D как 0.53, 0.59 и т. д. Насколько я понял нигде ничего не перемножается, чтобы получились такие дроби, а считаются только min, max и т. п.
А можно поподробнее рассказать, как рассчитываются матрицы Di?
А, понял.
Хотя у меня все равно результаты с Вашими не совпадают (зато совпадают с Авторскими), моя программа выдает следующее:
Хотя у меня все равно результаты с Вашими не совпадают (зато совпадают с Авторскими), моя программа выдает следующее:
0,50 0,60 0,70 0,80 0,90 1,00 1,00 1,00 1,00 1,00 1,00
0,40 0,50 0,60 0,70 0,80 0,90 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,90 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,70 0,80 0,90 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
----------------------------------------
0,50 0,53 0,59 0,66 0,75 0,85 0,96 1,00 1,00 1,00 1,00
0,70 0,73 0,79 0,86 0,95 1,00 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
----------------------------------------
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 0,70 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
----------------------------------------
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,50 0,51 0,54 0,59 0,66 0,75 0,86 0,99 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,90 0,91 0,94 0,99 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,90 0,91 0,94 0,99 1,00 1,00 1,00 1,00 1,00 1,00 1,00
----------------------------------------
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,75 0,85 0,95 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
0,99 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
----------------------------------------
1,00 1,00 1,00 1,00 1,00 1,00 1,00 0,90 0,80 0,70 0,60
1,00 1,00 1,00 1,00 1,00 1,00 1,00 0,90 0,80 0,70 0,60
1,00 1,00 1,00 1,00 1,00 1,00 0,90 0,80 0,70 0,60 0,50
1,00 1,00 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,10
1,00 1,00 1,00 1,00 0,90 0,80 0,70 0,60 0,50 0,40 0,30
Sign up to leave a comment.
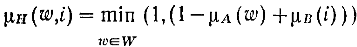

Многокритериальный выбор альтернатив с использованием правил нечеткого вывода. Реализация на Java. Часть 3/3: Пример