При разработке или исследовании готовых алгоритмов часто требуется определить качество их работы. Использовать для этой цели данные из реальных источников не всегда возможно, так как их свойства зачастую неизвестны и потому нельзя спрогнозировать результат выполнения исследуемых алгоритмов. В таком случае применяется моделирование данных по одному из хорошо известных законов распределения. Применяя исследуемый алгоритм к модельным данным, можно заранее предположить, каким окажется результат его выполнения. Если он окажется удовлетворительным, можно попробовать применить его и к реальным данным. Естественно, что это относится только к непараметрическим алгоритмам, то есть не зависящим от закона распределения данных.
Чаще всего используется моделирование данных, распределённых по нормальному закону. К сожалению, MS Excel и распространённые статистические пакетаы (SPSS, Statistica) позволяют моделировать только одномерные статистические распределения. Конечно, можно составить многомерное распределение из нескольких одномерных, но только в том случае, если переменные независимы. Если же нужно исследовать данные с зависящими друг от друга переменными, придётся писать программу.
Обычно указывают, что многомерное нормальное распределение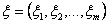 описывается вектором математических ожиданий
описывается вектором математических ожиданий 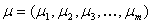 и положительно определённой ковариационной матрицей
и положительно определённой ковариационной матрицей 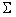 :
:

, где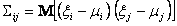 ;
;
i=1,2,3,…m, j=1,2,3,…, m;
m – количество признаков многомерной нормальной выборки.
Однако вместо ковариационной матрицы удобнее использовать корреляционную матрицу и вектор дисперсий
и вектор дисперсий 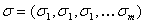 , поскольку коэффициент корреляции показывает степень связи между переменными, в отличие от коэффициента ковариации. Корреляционная матрица имеет вид:
, поскольку коэффициент корреляции показывает степень связи между переменными, в отличие от коэффициента ковариации. Корреляционная матрица имеет вид:
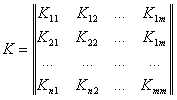
Преобразование коэффициентов матрицы к коэффициентам матрицы
к коэффициентам матрицы 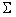 происходит по формуле:
происходит по формуле:

Для моделирования вектора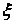 можно использовать линейное преобразование вектора
можно использовать линейное преобразование вектора  , компоненты которого есть нормально распределенные случайные величины с параметрами математического ожидания, равного нулю, и дисперсии, равной единице (т. е.
, компоненты которого есть нормально распределенные случайные величины с параметрами математического ожидания, равного нулю, и дисперсии, равной единице (т. е.  ). Для моделирования одномерной нормальной случайной величины есть множество способов, например, преобразование Бокса-Мюллера: при помощи двух случайных чисел
). Для моделирования одномерной нормальной случайной величины есть множество способов, например, преобразование Бокса-Мюллера: при помощи двух случайных чисел  и
и  , распределенных на интервале (0;1], при котором получаются одновременно два числа, распределенных по нормальному закону с параметрами
, распределенных на интервале (0;1], при котором получаются одновременно два числа, распределенных по нормальному закону с параметрами  :
:
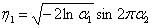

Преобразование в
в 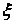 производится по формуле:
производится по формуле:

В данном преобразовании есть нижняя треугольная матрица, получающая из матрицы
есть нижняя треугольная матрица, получающая из матрицы 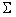 разложением Холецкого
разложением Холецкого  :
:
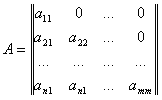
Каждый элемент матрицы определяется с помощью рекуррентной процедуры:
определяется с помощью рекуррентной процедуры:

, где индексы изменяются в диапазоне , а суммы с верхним нулевым приделом равны нулю (то есть, если
, а суммы с верхним нулевым приделом равны нулю (то есть, если 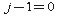 , то
, то  ,
,  ).
).
Описанное преобразование можно реализовать в виде двух функций на C++: основной функции normal_model(), реализующей алгоритм и вспомогательной matrix_determinant(), возвращающей определитель матрицы.
Функция normal_model() определяет количество требуемых переменных и значений из размерности матрицы с результатом. В случае успеха возвращает true, в случае неудачи – false.
Результат работы можно посмотреть тут. Обращение к функции происходит через механизм fastcgi.
Используемая литература:
Чаще всего используется моделирование данных, распределённых по нормальному закону. К сожалению, MS Excel и распространённые статистические пакетаы (SPSS, Statistica) позволяют моделировать только одномерные статистические распределения. Конечно, можно составить многомерное распределение из нескольких одномерных, но только в том случае, если переменные независимы. Если же нужно исследовать данные с зависящими друг от друга переменными, придётся писать программу.
Обычно указывают, что многомерное нормальное распределение
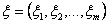 описывается вектором математических ожиданий
описывается вектором математических ожиданий 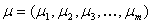 и положительно определённой ковариационной матрицей
и положительно определённой ковариационной матрицей 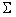 :
:
, где
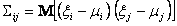 ;
;i=1,2,3,…m, j=1,2,3,…, m;
m – количество признаков многомерной нормальной выборки.
Однако вместо ковариационной матрицы удобнее использовать корреляционную матрицу
 и вектор дисперсий
и вектор дисперсий 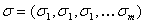 , поскольку коэффициент корреляции показывает степень связи между переменными, в отличие от коэффициента ковариации. Корреляционная матрица имеет вид:
, поскольку коэффициент корреляции показывает степень связи между переменными, в отличие от коэффициента ковариации. Корреляционная матрица имеет вид: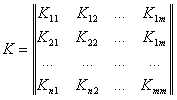
Преобразование коэффициентов матрицы
 к коэффициентам матрицы
к коэффициентам матрицы 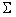 происходит по формуле:
происходит по формуле:
Для моделирования вектора
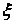 можно использовать линейное преобразование вектора
можно использовать линейное преобразование вектора  , компоненты которого есть нормально распределенные случайные величины с параметрами математического ожидания, равного нулю, и дисперсии, равной единице (т. е.
, компоненты которого есть нормально распределенные случайные величины с параметрами математического ожидания, равного нулю, и дисперсии, равной единице (т. е.  ). Для моделирования одномерной нормальной случайной величины есть множество способов, например, преобразование Бокса-Мюллера: при помощи двух случайных чисел
). Для моделирования одномерной нормальной случайной величины есть множество способов, например, преобразование Бокса-Мюллера: при помощи двух случайных чисел  и
и  , распределенных на интервале (0;1], при котором получаются одновременно два числа, распределенных по нормальному закону с параметрами
, распределенных на интервале (0;1], при котором получаются одновременно два числа, распределенных по нормальному закону с параметрами  :
: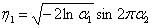

Преобразование
 в
в 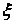 производится по формуле:
производится по формуле:
В данном преобразовании
 есть нижняя треугольная матрица, получающая из матрицы
есть нижняя треугольная матрица, получающая из матрицы 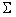 разложением Холецкого
разложением Холецкого  :
:
Каждый элемент матрицы
 определяется с помощью рекуррентной процедуры:
определяется с помощью рекуррентной процедуры:
, где индексы изменяются в диапазоне
 , а суммы с верхним нулевым приделом равны нулю (то есть, если
, а суммы с верхним нулевым приделом равны нулю (то есть, если 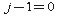 , то
, то  ,
,  ).
).Описанное преобразование можно реализовать в виде двух функций на C++: основной функции normal_model(), реализующей алгоритм и вспомогательной matrix_determinant(), возвращающей определитель матрицы.
Функция normal_model() определяет количество требуемых переменных и значений из размерности матрицы с результатом. В случае успеха возвращает true, в случае неудачи – false.
//Функция моделирования многомерных данных, распределённых по нормальному закону.
//double MatrixMath [mq] - вектор мат. ожидания
//double MatrixDisp [mq] - вектор диперсии
//vector<vector<double> > &correlation_matrix - корреляционная матрица
//vector<vector<double> > &MatrixRes - массив с результатом
bool normal_model (double MatrixMath[], double MatrixVar[], vector<vector<double> > &correlation_matrix, vector<vector<double> > &MatrixRes){
int mq =MatrixRes[0].size();//количество переменных
int count=MatrixRes.size();//количество значений
double MatrixA[mq][mq]; //треугольная матрица преобразований A
double MatrixN[count][mq]; //матрица случайных чисел, распределенных по нормальному закону с параметрами 0, 1
int i,j,k;
double suma, sumaa;
double alfa1, alfa2; //углы. Случайные числа, распределенные на интервале (0;1]
vector<vector<double> > MatrixK(mq); //Ковариационная матрица K
for (i=0;i<mq;i++){
MatrixK[i].resize(mq);
}
//Преобразование корреляционной матрицы в ковариационную
for (i=0; i<mq; i++){
for (j=0; j<mq; j++){
MatrixK[i][j]= correlation_matrix[i][j]* sqrt(MatrixVar[i]*MatrixVar[j]);
}
}
if (matrix_determinant(MatrixK)<=0) return false; // ошибка. Определитель ковариационной матрицы должен быть положительным;
//Заполнение матрицы A
for (i=0; i<mq; i++){
for (j=0; j<=i; j++){
sumA=0;
sumAA=0;
for (k=0; k<j; k++){
sumA+= MatrixA[i][k] * MatrixA[j][k];
sumAA+= MatrixA[j][k] * MatrixA[j][k];
}
MatrixA[i][j]=(MatrixK[i][j] - sumA)/ sqrt(MatrixK[j][j] - sumAA);
}
}
//моделирование случайных чисел, распределенных по нормальному закону с параметрами 0, 1
srand(time(NULL));
for (i=0; i<count; i+=2){
for (j=0; j<mq; j++){
alfa1 = (double)rand()/(RAND_MAX+1.0);
alfa2 = (double)rand()/(RAND_MAX+1.0);
if (!alfa1 || !alfa2){
j--;
}else{
MatrixN[i][j] = sqrt(-2*log(alfa1))*sin(2*M_PI*alfa2);
if (i+1<count) MatrixN[i+1][j] = sqrt(-2*log(alfa1))*cos(2*M_PI*alfa2);
}
}
}
//преобразование матрицы случайных чисел, распределенных по нормальному закону с параметрами 0, 1 к матрице с конечными параметрами
for (i=0; i<count; i++){
for (j=0; j<mq; j++){
MatrixRes[i][j]=MatrixMath[j];
for (k=0; k<mq; k++){
MatrixRes[i][j]+=MatrixA[j][k] * MatrixN[i][k];
}
}
}
return true;
}
//функция возвращает определитель матрицы m размерности N x N
double matrix_determinant (vector<vector<double> > & m){
double result=0;
if (m.size()==1){
return m[0][0];
}else if(m.size()==2){
return m[0][0] * m[1][1] - m[0][1] * m[1][0];
}else if(m.size()==3){
return m[0][0] * m[1][1] * m[2][2] + m[0][1] * m[1][2] * m[2][0] + m[0][2] * m[1][0] * m[2][1] - m[2][0] * m[1][1] * m[0][2] - m[1][0] * m[0][1] * m[2][2] - m[0][0] * m[2][1] * m[1][2];
}else{
vector<vector<double> > m1(m.size()-1);//массив N-1 x N-1, значения элементов матрицы порядка N-1
for (int i=0; i<m.size()-1; i++){
m1[i].resize(m.size()-1);
}
for (int i=0; i< m.size(); i++){
for (int j=1; j<m.size(); j++){
for (int k=0; k<m.size(); k++){
if (k<i){
m1[j-1][k] = m[j][k];
}else if(k>i){
m1[j-1][k-1] = m[j][k];
}
}
}
result+= pow(-1,i) *m[0][i] * matrix_determinant(m1);
}
}
return result;
}
Результат работы можно посмотреть тут. Обращение к функции происходит через механизм fastcgi.
Используемая литература:
- Мартышенко C.Н., Мартышенко Н.С., Кустов Д.А. Моделирование многомерных данных и компьютерный эксперимент. Техника и технология, 2007. – №2. С. 47–52.
- Ермаков С.М., Михайлов Г.А., Статистическое моделирование.М.: Наука, 1982.
- Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., т. 1-2, М., 1964-67.
- Rencher, Alvin C. (2002), Methods of Multivariate Analysis, Second Edition, John Wiley & Sons.