В комментариях к статьям N-е число Фибоначчи за O(log N) и Еще один алгоритм вычисления чисел Фибоначчи указывалось на тот факт, что уже 100-е число Фибоначчи не помещается в 4 байта, а в «длинной» арифметике скорость выполнения умножения резко просядет. Более того, были предположения, что примитивное сложение может оказаться быстрее. Я решил сравнить 2 алгоритма — простое сложение и алгоритм с логарифмическим количеством операций — и написал тестовую программу на С. Для «длинной» арифметики использовал библиотеку GMP.
Тестовая среда: VirtualBox, Athlon II X3 3,4 ГГц, 1Гб ОЗУ, Xubuntu 12.04 64bit, компилятор GCC 4.6.3, оптимизация O2
Второй алгоритм оказался намного быстрее. Я так и не смог дождаться, когда первый алгоритм посчитает миллиардное число Фибоначчи. Алгоритму №2 на это понадобилась 21 секунда.
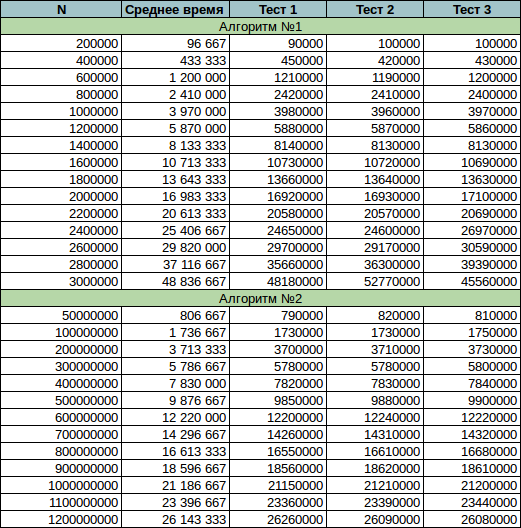
Результаты (указано время, возвращаемое функцией clock()):
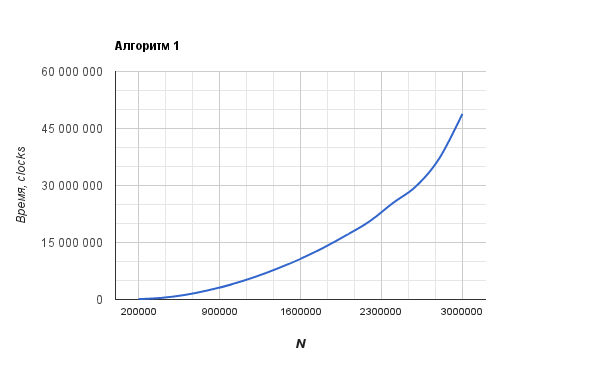
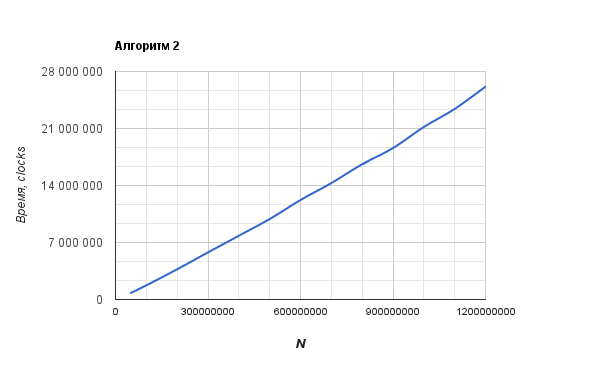
Второй график сильно похож на O(N). График первого алгоритма больше похож на O(N^2).
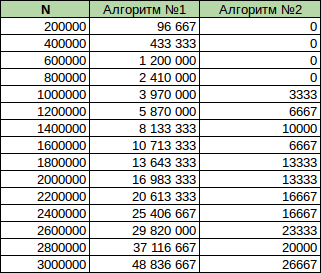
UPD Добавил совмещенный график. Второй алгоритм работает так быстро, что время его работы сравнимо с погрешностью функции clock()

Данные, на которых построен график:
Текст тестовой программы
Примитивный скрипт для запуска тестов
Входные данные:
#include <stdio.h> #include <stdlib.h> #include <time.h> #include <gmp.h> void fibonachi1(unsigned int n, mpz_t result); void fibonachi2(unsigned int n, mpz_t result); void dump(unsigned int n); int main(int argc, char* argv[]) { unsigned int n, test_count; clock_t t1, t2; mpz_t result; scanf("%u", &test_count); while (test_count--) { scanf("%u", &n); mpz_init(result); t1 = clock(); fibonachi1(n, result); t2 = clock(); printf("%u\t%u\n", n, (unsigned int)(t2 - t1)); mpz_clear(result); } scanf("%u", &test_count); while (test_count--) { scanf("%u", &n); mpz_init(result); t1 = clock(); fibonachi2(n, result); t2 = clock(); printf("%u\t%u\n", n, (unsigned int)(t2 - t1)); mpz_clear(result); } // dump(10000); return 0; } void fibonachi1(unsigned int n, mpz_t result) { mpz_t last, current; if (n < 2) { mpz_init_set_ui(result, n); } else { mpz_init_set_ui(last, 0); mpz_init_set_ui(current, 1); while (--n > 0) { mpz_swap(last, current); mpz_add(current, current, last); } mpz_swap(current, result); mpz_clear(last); mpz_clear(current); } } void fibonachi2(unsigned int n, mpz_t result) { mpz_t fn, fn1, gn, gn1; if (n < 2) { mpz_init_set_ui(result, n); } else { unsigned mask = 1, m = n; while (m > 1) { m >>= 1; mask <<= 1; } mpz_init_set_ui(fn, 1); mpz_init_set_ui(fn1, 1); mpz_init(gn); mpz_init(gn1); while (mask > 3) { mask >>= 1; mpz_swap(fn, gn); mpz_swap(fn1, gn1); if (n & mask) { mpz_mul(fn, gn1, gn1); mpz_set(fn1, fn); mpz_addmul(fn, gn, gn); mpz_mul(gn, gn, gn1); mpz_add(fn1, fn1, gn); mpz_add(fn1, fn1, gn); } else { mpz_mul(fn, gn, gn1); mpz_add(fn, fn, fn); mpz_mul(gn, gn, gn); mpz_sub(fn, fn, gn); mpz_mul(fn1, gn1, gn1); mpz_add(fn1, fn1, gn); } } if (mask > 1) { mask >>= 1; mpz_swap(fn, gn); mpz_swap(fn1, gn1); if (n & mask) { mpz_mul(fn, gn1, gn1); mpz_addmul(fn, gn, gn); } else { mpz_mul(fn, gn, gn1); mpz_add(fn, fn, fn); mpz_submul(fn, gn, gn); } } mpz_swap(result, fn); mpz_clear(fn1); mpz_clear(gn); mpz_clear(gn1); } } void dump(unsigned int n) { FILE* output; mpz_t result; mpz_init(result); fibonachi1(n, result); output = fopen("alg1.output", "w"); if (output) { mpz_out_str(output, 16, result); fclose(output); } mpz_clear(result); mpz_init(result); fibonachi2(n, result); output = fopen("alg2.output", "w"); if (output) { mpz_out_str(output, 16, result); fclose(output); } mpz_clear(result); }
Примитивный скрипт для запуска тестов
#!/bin/bash ./main <input.txt >test1.txt ./main <input.txt >test2.txt ./main <input.txt >test3.txt
Входные данные:
15 200000 400000 600000 800000 1000000 1200000 1400000 1600000 1800000 2000000 2200000 2400000 2600000 2800000 3000000 13 50000000 100000000 200000000 300000000 400000000 500000000 600000000 700000000 800000000 900000000 1000000000 1100000000 1200000000
Тестовая среда: VirtualBox, Athlon II X3 3,4 ГГц, 1Гб ОЗУ, Xubuntu 12.04 64bit, компилятор GCC 4.6.3, оптимизация O2
Второй алгоритм оказался намного быстрее. Я так и не смог дождаться, когда первый алгоритм посчитает миллиардное число Фибоначчи. Алгоритму №2 на это понадобилась 21 секунда.
Результаты (указано время, возвращаемое функцией clock()):

Второй график сильно похож на O(N). График первого алгоритма больше похож на O(N^2).


UPD Добавил совмещенный график. Второй алгоритм работает так быстро, что время его работы сравнимо с погрешностью функции clock()

Данные, на которых построен график:
