Эзотерические сортировки Дэвида Морган-Мара

Планировал написать про чё-нибудь эдакое мегаумное, если не про чётно-нечётную сортировку слиянием Батчера, то, на худой конец, про сортировку декартовым деревом. Но потом вспомнил, что грядёт череда торжеств, а значит стоит предложить что-нибудь праздничное, я бы даже сказал — легкомысленное.

Дэвид Морган-Мар

Весёлый гик из Австралии, астрофизик, математик, программист и изобретатель. Успел поработать в IBM, сейчас сотрудник Canon. Любитель комиксов, «Звёздных войн», путешествий, ненормального кодинга, миров GURPS. Автор нескольких эзотерических языков программирования (Chef, ZOMBIE, Piet и др.).

На персональном сайте Дэвида Моргана-Мара есть небольшая подборка «эзотерических сортировок», о которой грех не рассказать.

Абаковая сортировка
(Abacus sort)

Предположим, нужно отсортировать набор натуральных чисел. Выложим их друг под другом в виде горизонтальных рядов из камешков в соответствующем количестве. Сдвинем по вертикали до упора.

Собственно и всё.

Если пересчитаем камешки в каждом горизонтальном ряду, то мы получим первоначальный набор чисел в упорядоченном состоянии.

Про эту сортировку я уже подробно писал, поэтому сразу переходим к следующей.

Болотно-преболотная сортировка (Bogobogosort)

Традиционно самой медленной сортировкой считается так называемая болотная сортировка (Bogosort).



Перемешиваем массив до тех пор, пока его элементы не упорядочатся. Временная сложность — O(n x n!).

Разумеется, любой исключительно медленный алгоритм можно сделать ещё менее продуктивным. Если в Bogosort добавить хвостовую рекурсию при проверке подмассивов на упорядоченность, то даже самое гиблое болото можно утопить в ещё более огромной трясине. Ну, а если ещё рекурсивно клонировать проверяемые подмассивы и сортировать их до тех пор пока они не совпадут с оригиналом то многого можно достигнуть и в сложности по памяти.

Основной порядок действий — такой же как и у Bogosort:

1. Проверяем, отсортирован ли массив.
2. Если нет, то перемешиваем его и возвращаемся в пункт 1.

А вот проверка массива на упорядоченность производится следующим образом:

1. Создаётся копия массива.
2. Сортируются первые n-1 элементов копии с помощью Bogobogosort.
3. Проверяется, больше ли в копии n-й элемент чем первые n-1 элементов.
4. Если нет, то перемешиваем копию массива и возвращаемся в пункт 2.
5. Если да, то нужно ещё проверить, совпадает ли копия с оригиналом. Если совпадает, значит массив ни смотря ни на что отсортирован, если нет, то перемешиваем копию массива и идём в пункт 2.

Такое изощрённое издевательство над данными практически гарантирует что процесс будет продолжаться ну очень долго.

Кто не понял алгоритм, вот вам реализация

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class Bogobogosort {

	public static <T extends Comparable<T>> void sort(List<T> list) {
	
		if (list.size() <= 1) return;
		while (!isSorted(list)) Collections.shuffle(list);
		
	}

	public static <T extends Comparable<T>> boolean isSorted(List<T> list) {

		List<T> copy = new ArrayList<>(list);
		List<T> subList;
		
		do {		
			Collections.shuffle(copy);
			subList = copy.subList(0, copy.size() - 1);
			sort(subList);			
		} while (copy.get(copy.size() - 1).compareTo(subList.get(subList.size() - 1)) < 0);
		
		return copy.equals(list);
		
	}
}
/* Взято отсюда: https://github.com/lucaswerkmeister/Miscellaneous/blob/master/Sorting/src/Bogobogosort.java */

Что касается сложности по времени, Дэвид считает, что где-то порядка O(n!^n!). При тестировании на массиве из 7 элементов конечного результата он так и не дождался.

Сортировка «демона Максвелла» (Maxwell’s demon sort)

Метод сортировки основан на известном мысленном эксперименте великого английского физика XIX века Джеймса Клерка Максвелла. Данный способ аппаратно реализовать, опираясь на текущие достижения науки и техники, достаточно проблематично.

Ёмкость с газом разделена на две половины непроницаемой стенкой. В стенке есть отверстие, которое снабжено специальным устройством, которое назовём демоном Максвелла. Демон устроен так, что через отверстие он из левой части в правую пропускает только быстрые (горячие) молекулы газа, а из правой в левую — медленные (холодные) молекулы.

В результате функционирования данной системы якобы возникает парадокс, нарушающий Второе начало термодинамики: в сосуде исключительно за счёт внутренней энергии, без привлечения дополнительной, охлаждается левая часть и нагревается правая.

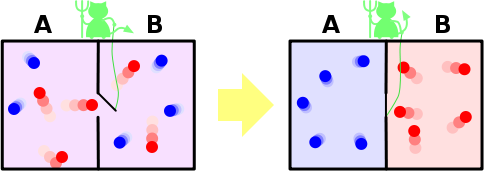
Возьмём сосуд с газом и рассмотрим все молекулы как неотсортированный набор чисел (каждое из которых — некое отображение энергии молекулы). Перегородим сосуд стенкой со встроенным в неё демоном Максвелла. Через некоторое время в правой части сосуда соберутся молекулы, чья энергия превышает некоторую заданную величину (или равна ей), а в левой части — молекулы, чья энергия меньше этой величины.

Разделим каждую половину сосуда на свои половинки с помощью стен со встроенными демонами Максвелла (для которых заданы другие пропускные значения). Таким образом мы дополнительно распределим молекулы на ещё более «горячие» и «холодные». И так мы дополнительными стенками со встроенными демонами Максвелла будем делить пространство внутри сосуда до тех пор, пока в каждой его ограниченной части не будут молекулы с одинаковой энергией. В этот момент все частицы окажутся «отсортированными».

Сортировка Джареда Даймонда (Jared Diamond’s sort)

«Алгоритм», базирующийся на книге Джареда Даймонда (Jared Diamond) «Ружья, микробы и сталь: Судьбы человеческих цивилизаций» («Guns, Germs, and Steel: The Fates of Human Societies»).

Данное произведение, удостоенное Пулитцеровской премии, является самым значительным трудом по географической антропологии за последние полтора десятилетия. Книгу высоко оценили социологи, историки и демографы. Под впечатлением остался и Билл Гейтс, не последний человек разбирающийся в глобальных мировых процессах: «Впечатляет… Эта книга закладывает основы понимания истории человечества».

Ввиду обширности затрагиваемых аспектов, даже краткий пересказ изложенных в книге идей не представляется возможным в узких рамках этой небольшой статьи. Интересующиеся без труда смогут на просторах всемирной паутины найти саму книгу, а также 3-х серийный документальный фильм, снятый в 2005 году каналом National Geographic.

Теперь алгоритм.

Для каждого числа из сортируемого списка определим примитивную цивилизацию охотников-собирателей, регион их дислокации заселим дикими животными (для последующего приручения) и растениями (для развития сельского хозяйства). Размер каждой локальной человеческой популяции, видовое разнообразие флоры и фауны — подбирать в прямой зависимости от соответствующего числа.

Позвольте развивать сельское хозяйство, промышленность, науку и культуру. То общество которое изобретёт и первым начнёт массово использовать огнестрельное оружие будет соответствовать в списке наибольшему элементу, относительно которого со временем упорядочатся все остальные.

Время выполнения зависит только от величины наибольшего числа, что позволяет формально утверждать о временной сложности O(1). На данный момент известен только один достоверный случай использования данной сортировки, затраченное время составило примерно 13000 лет. Эта величина была бы меньше, если бы наибольший элемент в массиве был бы больше.

Сортировка сбросами (Dropsort)

Дёшево и сердито: проходим по массиву и по пути удаляем (сбрасываем) из него неотсортированные элементы.



Весьма полезный, между прочим, хак со сложностью по времени O(n). Можете не благодар��ть.

Сортировка «Ханойская башня» (Tower of Hanoi sort)

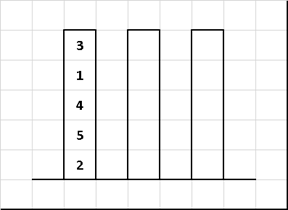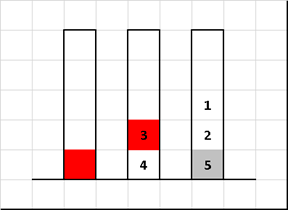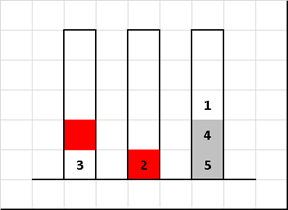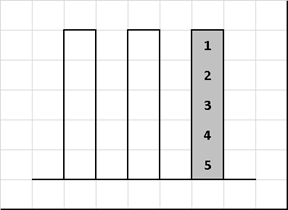
Алгоритм сортировки, основанный на знаменитой головоломке французского математика Эдуарда Люка.

Изменим только входное значение — диски на первом стержне необязательно должны быть в порядке «меньшие над большими». Остальные правила оставим как и в классике — за раз переносим только один диск, при этом нельзя «блины» большего диаметра класть на те, у которых размеры меньше. Требуется путём переноса дисков с одних стержней на другие в итоге собрать их в упорядоченной по размеру последовательности.

Данная сортировка интересна тем, что вырожденный случай для неё — это… полностью упорядоченный массив. Тогда мы имеем дело с эталонным «ханоем» для которого требуется выполнить 2ⁿ-1 перемещений. Наилучший случай по времени — реверс, в этом случае элементы один за другим сразу прыгают на свои места. И вообще, чем массив более близок к отсортированному состоянию, тем хуже — и наоборот!

Сортировка Разумного замысла (Intelligent Design Sort)

Поскольку для массива размером n возможно n! перестановок элементов, то вероятность того что элементы в нём будут следовать именно в том порядке в котором они следуют равна 1/n! что исчезающе мало. Абсурдно утверждать, что такое состояние массива возникло случайно.

Намного логичнее предположить, что есть некая высшая разумная сила, которая создала массив и расположила в нём элементы в определённом порядке. Нет никаких причин утверждать, что этот порядок не оптимален. Скорее всего элементы в структуре уже выстроены именно в той последовательности, в которой необходимо, даже если это противоречит нашим приземлённым и несовершенным представлениям о Порядке.

Более того — любые попытки «отсортировать» массив наверняка приведут к нарушению изначально заложенного в него совершенства.