Вчера на Хабре появился потрясающий по своей безграмотности пост "Возможны ли путешествия во времени". В ответ на моё замечание о незнакомстве с базовыми научными представлениями о пространстве и времени автор припечатал меня вот так:
Такого уровня воинствующего невежества я давно не видал, и уж на Хабре-то его видеть вдвойне странно.
Поскольку я, в отличие от автора, сциентист, то постараюсь в ответ рассказать любознательному читателю, что мы в действительности знаем о природе времени, причинности и путешествиях во времени.
В классической механике время считается абсолютным и неизменным в том смысле, что при переходе от одной системы отсчёта к другой временные интервалы не изменяются:




Здесь (x, y, z, t) — координаты в старой системе, (x', y', z', t') — координаты в новой системе. Здесь и далее предполагается (для упрощения формул), что одна система движется относительно другой параллельно оси x со скоростью v.
Это т.н. преобразования Галилея — что происходит с координатами при смене системы отсчета. В галилеевом смысле «поток времени» один на всю Вселенную, и временные координаты у всех объектов одинаковы. При этом классическая механика никак не трактует уникальность стрелы времени; более того, само понятие движения времени в ньютоновы формулы не входит никак.
В классической механике мы сами вводим движение от прошлого к будущему. Допустим, у нас задан набор материальных точек (координаты и скорости) и действующих сил. Далее мы задаёмся каким-то интервалом dt и смотрим, как система будет эволюционировать во времени. Никто не мешает нам двигаться в обратном направлении и следить, что происходило с системой в прошлом.
Однако «путешествие во времени» — т.е. перемещение одного конкретного объекта по шкале t в прошлое — ньютоновой механикой запрещено (см. выше — временной поток один на всю Вселенную).
Ситуация стала гораздо веселее, когда Максвелл сформулировал свою электродинамику, а затем Эйнштейн в попытках решить противоречия электродинамики и классической механики создал теорию относительности.
В рамках специальной теории относительности при переходе от одной инерциальной системы отсчета к другой мы пользуемся уже вот такими преобразованиями:
 ,
,
где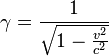 .
.
Здесь, как легко заметить, у каждой система отсчета «своя» шкала времени. В рамках СТО не сохраняются ни пространственный, ни временной интервал между точками — сохраняется только разность их квадратов:
ds2 = c2dt2 — dx2 — dy2 — dz2.
Что здесь записано? Это описание особого четырёхмерно��о псевдоевклидова пространства — т.н. пространства Минковского — в котором расстояние между точками равно разности квадратов разностей координат (а не сумме, как в обычном евклидовом пространстве).
С точки зрения СТО движение каждого тела представляет собой траекторию в четырёхмерном пространстве Минковского — т.н. «мировую линию».

Конусы на рисунке — это т.н. «световые конусы» — траектории объектов, движущихся со скоростью света.
Поскольку теперь время у каждого объекта своё — и, более того, оно вольно изменяться как угодно — мы, теоретически, можем допустить «развороты» мировой линии, т.е. путешествие во времени.
(Путешествовать во времени вперёд в СТО очень легко — достаточно двигаться со скоростью, близкой к световой — и этот эффект, хоть и в микроскопических масштабах, успешно подтверждён. Поэтому мы говорим здесь и далее о путешествии во времени в смысле путешествия во времени назад)
Однако здесь есть две большие проблемы.
Первая заключается в том, что материальный объект никогда не сможет достигнуть границы светового конуса — для этого требуется приложить бесконечное количество энергии.
Вторая заключается в любопытных особенностях лоренцовых преобразований. Допустим, мы смогли переместить объект из точки A в точку B быстрее скорости света. Тогда обязательно найдётся такая система отсчёта, в которой объект сначала появится в точке B, а потом отбудет из точки A. Проще говоря, движение быстрее света и ��сть перемещение во времени в СТО, да только вот в очень нетривиальном смысле.
Действительно, как понимать вот это «найдётся такая система»? Получается, что для части наблюдателей перемещение в прошлое есть, а для части — нет. Это зависит исключительно от скорости перемещения наблюдателя.
И, во-вторых, получается полное безумие с причиной и следствием. Очевидно, что появление объекта в точке B — следствие его отбытия из точки A. Но для каких-то наблюдателей следствие происходит позже, чем причина. А для каких-то — раньше. К этому вопросу мы ещё вернёмся.
В итоге в СТО движение со скоростью быстрее света запрещено. Нет, точнее, не так: запрещён перенос информации между объектами, находящимися вне светового конуса друг друга. Иначе СТО сталкивается с неразрешимыми противоречиями.
Движение изначально быстрее света разрешено — при условии, что двигающиеся быстрее света системы не обмениваются информацией. Например, теория инфляций предполагает, что в самом начале большого взрыва семейство новорожденных Вселенных удалялось друг от друга со скоростью, многократно превышающей световую. И никакого противоречия здесь нет — т.к. Вселенные удаляются друг от друга быстрее света, свет из одной из них никогда не достигнет другой, и информация никогда не будет передана.
Вернёмся, однако, к нашим баранам, т.е. к дискуссии о природе времени. Признаться, СТО внесла совсем немного понимания в этот вопрос. Что такое «внутреннее время» объекта и как оно измеряется? Почему временная координата пространства Минковского так существенно противопоставленна пространственным? Наконец, что это за зверь такой «инерциальная система отсчета» и где его взять в реальности?
Понимал все эти трудности и Эйнштейн, и поэтому десятью годами позже создал общую теорию относительности (ОТО), которая окончательно всё запутала.
Итак, для начала, все координаты в ОТО (включая временную) — это просто номера точек на оси. У них нет больше никакого смысла, задавайте любые.
Далее, в этих координатах для каждой точки пространства-времени необходимо определить т.н. фундаментальный метрический тензор gab. Что это за зверь? Это матрица 4х4, которая определяет расстояние между соседними точками. Допустим, вы находитесь в некоторой точке (x0, x1, x2, x3) и перемещаетесь в направлении (dx0, dx1, dx2, dx3). Тогда вы пройдёте расстояние:

Здесь и далее по повторяющимся сверху и снизу индексам подразумевается суммирование, т.е. на самом деле здесь записана сумма 16 компонент.
Для обычного Евклидова пространства с ортонормированным базисом матрица g равна единичной. В пространстве Минковского g00 = 1, g11 = g22 = g33 = -1.
В пространстве ОТО компоненты метрического тензора могут быть абсолютно какими угодно. Т.е. расстояние между соседними точками — (почти) произвольная функция от разности координат. Ну, координаты же у нас совершенно условны, помните?
Если вдруг мы хотим перейти от одной системы координат к другой, все тензоры (включая фундаментальный метрический) претерпят вот такие изменения:

В общем, это была лёгкая часть :). Короче говоря, в ОТО вы можете задаться совершенно любыми координатами и совершенно любой точкой отсчёта, единственное что вам придётся вычислить фундаментальный метрический тензор. Вопрос про то «чем измерять уникальное время объекта» как бы не стоит — нумеруйте моменты времени как душе угодно.
Итак, про пространственно-временную геометрию вроде как выяснили, перейдём теперь к объектам в этом пространстве. Из распределения импульсов и энергий тел нам нужно сформировать т.н. тензор энергии-импульса Tab. Он точно так же свой в каждой точке пространства-времени и задаёт «плотности» масс и энергий.
Наконец, нам нужны производные фундаментального тензора по всем направлениям и производные (скорости) всех объектов.
Теперь мы можем сформулировать, как взаимно влияют друг на друга геометрия пространства и движения тел.
Геометрия пространства изменяется следующим образом:

Это уравнение известно как уравнение Гильберта-Эйнштейна. Здесь Rab — т.н. тензор Риччи, выражаемый через вторые частные производные фундаментального метрического тензора. (Кстати, Григорий Перельман мимоходом доказал теорему Пуанкаре в своих работах, посвящённых как раз потокам тензора Риччи.)
Что здесь написано? Зная тензор энергии-импульса, метрический тензор и производные метрического тензора мы можем рассчитать вторые производные метрического тензора. Таким образом, мы определяем, как энергия и импульс влияют на геометрию пространства.
Теперь обратно. Чтобы определить, как геометрия пространства влияет на движение объектов в нём, мы устремляем для каждой материальной точки проходимое ей расстояние ds2 → min. Раскрывая это условие (например, через принцип Лагранжа), мы получим выражения для вторых производных («ускорений») объектов. В частности, для безмассовых частиц (света) движение происходит по геодезической линии, выражаемой следующим уравнением:
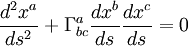
Здесь Гabc — т.н. символы Кристоффеля, выражаемые через метрический тензор.
Существует довольно изящная аналогия, описывающая смысл такого движения в понятных терминах. Представьте себе, что мы натянули простынь и в некоторых точках положили тяжёлые шары. В этих местах простынь прогнулась и искривилась — подобно тому, как искривляется пространство в присутствии энергии и импульса.
Теперь катнём по нашей простыне лёгкий шарик. На ровных участках он будет двигаться по прямой; но, приближаясь к массивным точкам, он будет искривлять свою траекторию так, будто бы тяжёлые шары его «притянули». Это и есть эффект притяжения, на самом деле вызванный искривлением «пространства», в котором движется шарик.
Уффф. Ок, подведём итог, как движутся объекты с точки зрения ОТО:
— мы должны знать текущую геометрию пр��странства (метрический тензор) и положения энергий и импульсов в нём (тензор энергии-импульса);
— мы, кроме того, должны знать «скорости», т.е. первые частные производные, и того, и другого;
— тогда мы можем вычислить вторые производные и метрического тензора, и мировых линий объектов, и, соответственно, сделать шаг моделирования.
Здесь, правда, кроется один очень неприятный момент. Задаться каким-то исходным состоянием системы не очень-то просто: легко может оказаться, что такое положение попросту недопустимо. Алгоритма, позволяющего конструировать состояния, нет — сумма двух допустимых состояний может оказаться недопустимым состоянием. Точных аналитических решений уравнений Гильберта-Эйнштейна существует ровно четыре: метрики Шварцшильда, Керра, Райснера-Нордстрёма и Керра-Ньюмана, которые описывают пространство с одной материальной вращающейся/невращающейся заряженной/незаряженной точкой.
Численное решение уравнений тоже маловозможно ввиду потрясающей их сложности: для каждой точки четырёхмерного пространства нужно хранить по четыре 16-значных матрицы и решать 32 уравнения в каждый шаг, что на современных мощностях невозможно со сколько-нибудь приемлемой точностью.
Закончили с общей теорией, перейдём к более частным вопросам. Запрещает ли ОТО движение с убыванием времени? Вообще нет. Устремляя ds2 → min мы в каких-то условиях можем получить dt < 0 для оптимальной траектории движения. Попытаться формализовать эти «какие-то условия», мягко говоря, непросто; в частности, можно предположить существование такого феномена как «кротовые норы» — особые искажения геометрии пространства, позволяющие путешествовать (возможно, даже безопасно для человека) со скоростями быстрее света (что эффективно и есть путешествие в прошлое — в некотором смысле).
Прояснила ли ОТО природу времени? Это как посмотреть. С одной стороны, пространство, время, энергия и импульс обрели новые смыслы в рамках теории. С другой стороны, вопросы к ОТО формулируются как-то совсем не так просто и понятно, как к ньютоновской механике. Например, вся ОТО ковариантна — записана через тензоры с нижними индексами (тензоры с верхними индексами называются контравариантными). Да, я забыл уточнить — просто так менять положение индекса нельзя :), меняется выражение для перехода от одной координатной системы к другой. Так вот, почему ОТО ковариантна — один из больших философских вопросов, на который не то что ответить — осознать-то не очень просто. Потому что.
Если посмотреть на современные более «продвинутые» теории — струнные — то они, в целом, про то же. Только оперируют уже не четырехмерным, а 10- или даже 11-мерным пространством (в котором все измерения, кроме четырёх, «свёрнуты» так, что имеют для нас нулевой размер). В этом пространстве рассматриваются многомерные поверхности (браны — многомерные мембраны), по которым движутся объекты-струны. Объект движется так, чтобы его траектория «заметала» минимальную «площадь» на поверхности «браны». Это если утрировать. Смысл, на самом деле, примерно тот же, только размерностей больше.
Здесь ещё можно рассказать про время в квантовой механике — но увольте, это уже за рамками моих возможностей. Там в этом месте почти ничего интересного (квантовая механика в этом смысле более классична чем ОТО — её законы явно записаны как производные по времени), кроме того, что временная координата объекта — как и пространственная — подчиняется соотношению неопределённостей и не может быть определена в паре с энергией абсолютно точно.
Вот теперь пришло время вернуться к принципу причинности. Мы видим, что ОТО не даёт никакого инсайта в этом месте. Причинности как бы не существует. Но мы-то с вами отлично знаем, что она ещё как существует, мы её очень даже видим в том мире, который дан нам в ощущениях.
ОТО (и струнные теории) всё окончательно запутали. Если ньютонова механика явно не разрешала никаких таких путешествий во времени, то ОТО прямо говорит: путешествиям во времени мешает только принцип причинности и ничего более. Математически ничто не запрещает.
Отсюда для получения какого-то научного ответа на этот вопрос придётся разобраться в смысле принципа причинности. Увы, пока в этом месте наблюдается исключительно туман войны.
Есть одна теория, которая идёт именно от причинности как от основы мироздания. Это т.н. теория причинной динамической триангуляции, которая строит пространство причинных зависимостей событий. (Опять утрирую, подробее гуглите/яндексуйте.) Увы, ничем эта теория особо не примечательна, никаких особых инсайтов не даёт — струнные теории пока выглядят интереснее. Впрочем, у некоторых физиков иное мнение — см. Ли Смолин, «Неприятности с физикой: взлет теории струн, упадок науки и что за этим следует».
Что в итоге? В итоге я вас всех обманул. Я вот прям сильно удивлюсь, если вам стало хоть чуть-чуть понятнее, как устроено время и возможны ли путешествия в нём; я и сам вконец запутался, пока писал сей очерк. Надеюсь зато, что вы теперь представляете масштаб проблемы и осознаёте, что невозможно решить её с наскока, нафантазировав всякой ерунды :).
Если для Вас википедия — главный оплот истины и знаний, а физические законы непоколебимы — Вам пора на работу в инквизицию. Еще столько людей, опровергающих теоретические выдумки физиков 18 века, не сожжено!
Такого уровня воинствующего невежества я давно не видал, и уж на Хабре-то его видеть вдвойне странно.
Поскольку я, в отличие от автора, сциентист, то постараюсь в ответ рассказать любознательному читателю, что мы в действительности знаем о природе времени, причинности и путешествиях во времени.
Время
В классической механике время считается абсолютным и неизменным в том смысле, что при переходе от одной системы отсчёта к другой временные интервалы не изменяются:




Здесь (x, y, z, t) — координаты в старой системе, (x', y', z', t') — координаты в новой системе. Здесь и далее предполагается (для упрощения формул), что одна система движется относительно другой параллельно оси x со скоростью v.
Это т.н. преобразования Галилея — что происходит с координатами при смене системы отсчета. В галилеевом смысле «поток времени» один на всю Вселенную, и временные координаты у всех объектов одинаковы. При этом классическая механика никак не трактует уникальность стрелы времени; более того, само понятие движения времени в ньютоновы формулы не входит никак.
В классической механике мы сами вводим движение от прошлого к будущему. Допустим, у нас задан набор материальных точек (координаты и скорости) и действующих сил. Далее мы задаёмся каким-то интервалом dt и смотрим, как система будет эволюционировать во времени. Никто не мешает нам двигаться в обратном направлении и следить, что происходило с системой в прошлом.
Однако «путешествие во времени» — т.е. перемещение одного конкретного объекта по шкале t в прошлое — ньютоновой механикой запрещено (см. выше — временной поток один на всю Вселенную).
Ситуация стала гораздо веселее, когда Максвелл сформулировал свою электродинамику, а затем Эйнштейн в попытках решить противоречия электродинамики и классической механики создал теорию относительности.
В рамках специальной теории относительности при переходе от одной инерциальной системы отсчета к другой мы пользуемся уже вот такими преобразованиями:
 ,
,где
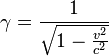 .
.Здесь, как легко заметить, у каждой система отсчета «своя» шкала времени. В рамках СТО не сохраняются ни пространственный, ни временной интервал между точками — сохраняется только разность их квадратов:
ds2 = c2dt2 — dx2 — dy2 — dz2.
Что здесь записано? Это описание особого четырёхмерно��о псевдоевклидова пространства — т.н. пространства Минковского — в котором расстояние между точками равно разности квадратов разностей координат (а не сумме, как в обычном евклидовом пространстве).
С точки зрения СТО движение каждого тела представляет собой траекторию в четырёхмерном пространстве Минковского — т.н. «мировую линию».

Конусы на рисунке — это т.н. «световые конусы» — траектории объектов, движущихся со скоростью света.
Поскольку теперь время у каждого объекта своё — и, более того, оно вольно изменяться как угодно — мы, теоретически, можем допустить «развороты» мировой линии, т.е. путешествие во времени.
(Путешествовать во времени вперёд в СТО очень легко — достаточно двигаться со скоростью, близкой к световой — и этот эффект, хоть и в микроскопических масштабах, успешно подтверждён. Поэтому мы говорим здесь и далее о путешествии во времени в смысле путешествия во времени назад)
Однако здесь есть две большие проблемы.
Первая заключается в том, что материальный объект никогда не сможет достигнуть границы светового конуса — для этого требуется приложить бесконечное количество энергии.
Вторая заключается в любопытных особенностях лоренцовых преобразований. Допустим, мы смогли переместить объект из точки A в точку B быстрее скорости света. Тогда обязательно найдётся такая система отсчёта, в которой объект сначала появится в точке B, а потом отбудет из точки A. Проще говоря, движение быстрее света и ��сть перемещение во времени в СТО, да только вот в очень нетривиальном смысле.
Действительно, как понимать вот это «найдётся такая система»? Получается, что для части наблюдателей перемещение в прошлое есть, а для части — нет. Это зависит исключительно от скорости перемещения наблюдателя.
И, во-вторых, получается полное безумие с причиной и следствием. Очевидно, что появление объекта в точке B — следствие его отбытия из точки A. Но для каких-то наблюдателей следствие происходит позже, чем причина. А для каких-то — раньше. К этому вопросу мы ещё вернёмся.
В итоге в СТО движение со скоростью быстрее света запрещено. Нет, точнее, не так: запрещён перенос информации между объектами, находящимися вне светового конуса друг друга. Иначе СТО сталкивается с неразрешимыми противоречиями.
Движение изначально быстрее света разрешено — при условии, что двигающиеся быстрее света системы не обмениваются информацией. Например, теория инфляций предполагает, что в самом начале большого взрыва семейство новорожденных Вселенных удалялось друг от друга со скоростью, многократно превышающей световую. И никакого противоречия здесь нет — т.к. Вселенные удаляются друг от друга быстрее света, свет из одной из них никогда не достигнет другой, и информация никогда не будет передана.
Вернёмся, однако, к нашим баранам, т.е. к дискуссии о природе времени. Признаться, СТО внесла совсем немного понимания в этот вопрос. Что такое «внутреннее время» объекта и как оно измеряется? Почему временная координата пространства Минковского так существенно противопоставленна пространственным? Наконец, что это за зверь такой «инерциальная система отсчета» и где его взять в реальности?
Понимал все эти трудности и Эйнштейн, и поэтому десятью годами позже создал общую теорию относительности (ОТО), которая окончательно всё запутала.
Итак, для начала, все координаты в ОТО (включая временную) — это просто номера точек на оси. У них нет больше никакого смысла, задавайте любые.
Далее, в этих координатах для каждой точки пространства-времени необходимо определить т.н. фундаментальный метрический тензор gab. Что это за зверь? Это матрица 4х4, которая определяет расстояние между соседними точками. Допустим, вы находитесь в некоторой точке (x0, x1, x2, x3) и перемещаетесь в направлении (dx0, dx1, dx2, dx3). Тогда вы пройдёте расстояние:

Здесь и далее по повторяющимся сверху и снизу индексам подразумевается суммирование, т.е. на самом деле здесь записана сумма 16 компонент.
Для обычного Евклидова пространства с ортонормированным базисом матрица g равна единичной. В пространстве Минковского g00 = 1, g11 = g22 = g33 = -1.
В пространстве ОТО компоненты метрического тензора могут быть абсолютно какими угодно. Т.е. расстояние между соседними точками — (почти) произвольная функция от разности координат. Ну, координаты же у нас совершенно условны, помните?
Если вдруг мы хотим перейти от одной системы координат к другой, все тензоры (включая фундаментальный метрический) претерпят вот такие изменения:

В общем, это была лёгкая часть :). Короче говоря, в ОТО вы можете задаться совершенно любыми координатами и совершенно любой точкой отсчёта, единственное что вам придётся вычислить фундаментальный метрический тензор. Вопрос про то «чем измерять уникальное время объекта» как бы не стоит — нумеруйте моменты времени как душе угодно.
Итак, про пространственно-временную геометрию вроде как выяснили, перейдём теперь к объектам в этом пространстве. Из распределения импульсов и энергий тел нам нужно сформировать т.н. тензор энергии-импульса Tab. Он точно так же свой в каждой точке пространства-времени и задаёт «плотности» масс и энергий.
Наконец, нам нужны производные фундаментального тензора по всем направлениям и производные (скорости) всех объектов.
Теперь мы можем сформулировать, как взаимно влияют друг на друга геометрия пространства и движения тел.
Геометрия пространства изменяется следующим образом:

Это уравнение известно как уравнение Гильберта-Эйнштейна. Здесь Rab — т.н. тензор Риччи, выражаемый через вторые частные производные фундаментального метрического тензора. (Кстати, Григорий Перельман мимоходом доказал теорему Пуанкаре в своих работах, посвящённых как раз потокам тензора Риччи.)
Что здесь написано? Зная тензор энергии-импульса, метрический тензор и производные метрического тензора мы можем рассчитать вторые производные метрического тензора. Таким образом, мы определяем, как энергия и импульс влияют на геометрию пространства.
Теперь обратно. Чтобы определить, как геометрия пространства влияет на движение объектов в нём, мы устремляем для каждой материальной точки проходимое ей расстояние ds2 → min. Раскрывая это условие (например, через принцип Лагранжа), мы получим выражения для вторых производных («ускорений») объектов. В частности, для безмассовых частиц (света) движение происходит по геодезической линии, выражаемой следующим уравнением:
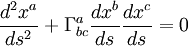
Здесь Гabc — т.н. символы Кристоффеля, выражаемые через метрический тензор.
Существует довольно изящная аналогия, описывающая смысл такого движения в понятных терминах. Представьте себе, что мы натянули простынь и в некоторых точках положили тяжёлые шары. В этих местах простынь прогнулась и искривилась — подобно тому, как искривляется пространство в присутствии энергии и импульса.
Теперь катнём по нашей простыне лёгкий шарик. На ровных участках он будет двигаться по прямой; но, приближаясь к массивным точкам, он будет искривлять свою траекторию так, будто бы тяжёлые шары его «притянули». Это и есть эффект притяжения, на самом деле вызванный искривлением «пространства», в котором движется шарик.
Уффф. Ок, подведём итог, как движутся объекты с точки зрения ОТО:
— мы должны знать текущую геометрию пр��странства (метрический тензор) и положения энергий и импульсов в нём (тензор энергии-импульса);
— мы, кроме того, должны знать «скорости», т.е. первые частные производные, и того, и другого;
— тогда мы можем вычислить вторые производные и метрического тензора, и мировых линий объектов, и, соответственно, сделать шаг моделирования.
Здесь, правда, кроется один очень неприятный момент. Задаться каким-то исходным состоянием системы не очень-то просто: легко может оказаться, что такое положение попросту недопустимо. Алгоритма, позволяющего конструировать состояния, нет — сумма двух допустимых состояний может оказаться недопустимым состоянием. Точных аналитических решений уравнений Гильберта-Эйнштейна существует ровно четыре: метрики Шварцшильда, Керра, Райснера-Нордстрёма и Керра-Ньюмана, которые описывают пространство с одной материальной вращающейся/невращающейся заряженной/незаряженной точкой.
Численное решение уравнений тоже маловозможно ввиду потрясающей их сложности: для каждой точки четырёхмерного пространства нужно хранить по четыре 16-значных матрицы и решать 32 уравнения в каждый шаг, что на современных мощностях невозможно со сколько-нибудь приемлемой точностью.
Закончили с общей теорией, перейдём к более частным вопросам. Запрещает ли ОТО движение с убыванием времени? Вообще нет. Устремляя ds2 → min мы в каких-то условиях можем получить dt < 0 для оптимальной траектории движения. Попытаться формализовать эти «какие-то условия», мягко говоря, непросто; в частности, можно предположить существование такого феномена как «кротовые норы» — особые искажения геометрии пространства, позволяющие путешествовать (возможно, даже безопасно для человека) со скоростями быстрее света (что эффективно и есть путешествие в прошлое — в некотором смысле).
Прояснила ли ОТО природу времени? Это как посмотреть. С одной стороны, пространство, время, энергия и импульс обрели новые смыслы в рамках теории. С другой стороны, вопросы к ОТО формулируются как-то совсем не так просто и понятно, как к ньютоновской механике. Например, вся ОТО ковариантна — записана через тензоры с нижними индексами (тензоры с верхними индексами называются контравариантными). Да, я забыл уточнить — просто так менять положение индекса нельзя :), меняется выражение для перехода от одной координатной системы к другой. Так вот, почему ОТО ковариантна — один из больших философских вопросов, на который не то что ответить — осознать-то не очень просто. Потому что.
Если посмотреть на современные более «продвинутые» теории — струнные — то они, в целом, про то же. Только оперируют уже не четырехмерным, а 10- или даже 11-мерным пространством (в котором все измерения, кроме четырёх, «свёрнуты» так, что имеют для нас нулевой размер). В этом пространстве рассматриваются многомерные поверхности (браны — многомерные мембраны), по которым движутся объекты-струны. Объект движется так, чтобы его траектория «заметала» минимальную «площадь» на поверхности «браны». Это если утрировать. Смысл, на самом деле, примерно тот же, только размерностей больше.
Здесь ещё можно рассказать про время в квантовой механике — но увольте, это уже за рамками моих возможностей. Там в этом месте почти ничего интересного (квантовая механика в этом смысле более классична чем ОТО — её законы явно записаны как производные по времени), кроме того, что временная координата объекта — как и пространственная — подчиняется соотношению неопределённостей и не может быть определена в паре с энергией абсолютно точно.
Вот теперь пришло время вернуться к принципу причинности. Мы видим, что ОТО не даёт никакого инсайта в этом месте. Причинности как бы не существует. Но мы-то с вами отлично знаем, что она ещё как существует, мы её очень даже видим в том мире, который дан нам в ощущениях.
ОТО (и струнные теории) всё окончательно запутали. Если ньютонова механика явно не разрешала никаких таких путешествий во времени, то ОТО прямо говорит: путешествиям во времени мешает только принцип причинности и ничего более. Математически ничто не запрещает.
Отсюда для получения какого-то научного ответа на этот вопрос придётся разобраться в смысле принципа причинности. Увы, пока в этом месте наблюдается исключительно туман войны.
Есть одна теория, которая идёт именно от причинности как от основы мироздания. Это т.н. теория причинной динамической триангуляции, которая строит пространство причинных зависимостей событий. (Опять утрирую, подробее гуглите/яндексуйте.) Увы, ничем эта теория особо не примечательна, никаких особых инсайтов не даёт — струнные теории пока выглядят интереснее. Впрочем, у некоторых физиков иное мнение — см. Ли Смолин, «Неприятности с физикой: взлет теории струн, упадок науки и что за этим следует».
Что в итоге? В итоге я вас всех обманул. Я вот прям сильно удивлюсь, если вам стало хоть чуть-чуть понятнее, как устроено время и возможны ли путешествия в нём; я и сам вконец запутался, пока писал сей очерк. Надеюсь зато, что вы теперь представляете масштаб проблемы и осознаёте, что невозможно решить её с наскока, нафантазировав всякой ерунды :).