Некриптографические хеш-функции и DoS атака на них / Habr

Некриптографические хеш-функции применяются там, где важна скорость и не так важна возможность атаки на характеристики функции. Последнее время активно обсуждается атака на алгоритмическую сложность хеш-таблиц путём создания множественных коллизий хеш-функции, которая может привести к DoS. Мы рассмотрим современные некриптографические хеш-функции, условия для их применения, возможные методы защиты от атаки на хеш-таблицы и почему оказалось, что это не так просто исправить.

Лавинный эффект хеш-функции One-at-a-Time

Некриптографические хеш-функции

Если криптографические хеш-функции у всех на слуху, то про некриптографические (хеш-функции общего назначения) известно мало. Некриптографические функции применяются там, где на данные не воздействуют третьи лица (злоумышленник). Например, такие функции могут использоваться для построения хеш-таблиц.

Критерии, которые важны для некриптографических хеш-функций:

Выходные значения должны иметь равномерное распределение (uniform distribution). Этот критерий важен для построения хеш-таблиц, чтобы скорость поиска была оптимальна.
Каждый входной бит должен в 50% случаев влиять на каждый выходной бит (avalanche — лавинный критерий). Этот критерий важен для использования хеша в качестве уникального идентификатора документа. Также, иногда хеш может иметь равномерное распределение, но проваливать лавинный критерий — в этом случае будут ключи, для которых хеш не будет давать равномерное распределение.
Между парами бит на выходе не должно быть корреляции. Это рассматривать не будем, т.к. обычно с этим критерием проблемы нет.
Скорость. Все перечисленные хеши на порядок быстрее, чем криптографические.

Поскольку обычно пространство входных значений больше пространства выходных значений, то коллизии неизбежны. У идеальной функции выходные значения имеют равномерное распределение, поэтому вероятность коллизий минимальная. Это можно проверить хи-квадрат тестом (χ²).

FNV-1a

2003 год. Скорость: 4.5 циклов на байт.
Очень простая функция [1] (RFC [5]).
1. Равномерное распределение: плохое, может использоваться до 14 бит для хеш-таблицы (до 2¹⁴ слотов хеш-таблицы). Чуть-чуть лучше в вариации FNV-1a, которая рекомендуется по умолчанию.
2. Лавинный критерий: плохо. Также плохо и в FNV-1a.
Оба критерия значительно улучшены в модифицированном FNV-1a [2], где к FNV-1a добавлены перемешивания в конце.

Bob Jenkins' Hash (lookup3)

2006 год, длина 32 и 64 бита, 32-битные инструкции, скорость: 2.62 цикла на байт (для сообщений длиной 16 байт).
1. Равномерное распределение: отличное для всех бит.
2. Лавинный критерий: хорошо. Есть небольшая проблема с верхними битами.
Первый вариант функции назывался One-at-a-Time.

CRC32

1975 год, длина: 32, 64 и 128 бит, скорость: 1.2–0.13 цикла на байт (для сообщений короче 64 бит, в зависимости от CPU).
1. Равномерное распределение: плохое распределение нижних бит. Используйте верхние биты для хеш-таблицы, тогда можно использовать все протестированные биты — до 16 верхних бит (до 2¹⁶ слотов хеш-таблицы).
2. Лавинный критерий: очень плохо. Лавинный эффект отсутствует. Сказывается назначение хеша: его выходные биты спроектированы так, чтобы обнаруживать ошибки в канале передачи данных. Также, у CRC есть важное свойство: можно разбить сообщение на части, посчитать хеш для каждой части, потом объединить сообщение, и посчитать хеш всего сообщения из хешей его частей.

MurmurHash 2

2008 год, длина 32 и 64 бита, 32 и 64-битные инструкции.
Есть проблема с равномерностью распределения некоторых ключей [3].

MurmurHash 3

2011 год, длина 32 и 128 бит, 32 и 64-битные инструкции, скорость: 1.87 циклов на байт (для сообщений длиной 16 байт).
1. Равномерное распределение: хорошее (в одном случае из трёх «почти подозрительное»).
2. Лавинный критерий: отлично.

Зависимость скорости хеш-функции от длины ключа хеша

Зависимость скорости хеш-функции от длины ключа хеша

CityHash

2011 год, длина 32, 64, 128 и 256 бит, 64-битные ��нструкции. Достаточно сложная функция.
Для самого быстрого варианта нужны CRC32 инструкции процессора (SSE 4.2 — Intel Nehalem).
1. Равномерное распределение: хорошее (в одном случае из трёх «почти подозрительное»).
2. Лавинный критерий: хорошо. Есть небольшая проблема с нижними битами.

SpookyHash

2011 год, длина 32, 64 и 128 бит, скорость: 0.33 цикла на байт. Автор Bob Jenkins.
1. Равномерное распределение: среднее (в одном случае из трёх «подозрительное»).
2. Лавинный критерий: отлично.

Статистический анализ хеш-функций можно сделать при помощи инструментов [17], использовались результаты анализа [2], [4], [18].

CityHash более сложный и имеет бо́льшую пропускную способность (скорость на длинных сообщениях), чем MurmurHash. MurmurHash более простой, имеет низкую задержку для коротких сообщений (< 20 байт).

CityHash использует инструкции CRC у новых процессоров, обеспечивая до 0.17 циклов на байт, что быстрее всех остальных хешей; для сравнения, SHA-1 — 4.6 циклов на байт (Ivy Bridge). Без поддержки этих инструкций CityHash в два раза медленнее SpookyHash (по мнению автора последнего).

Для 32-битной платформы MurmurHash 3 может быть быстрее, чем SpookyHash и CityHash.

Идеальная хеш-функция

Если массив сообщений заранее известен, то можно использовать идеальную хеш-функцию: без коллизий и с поиском в одну операцию сравнения. Пример: gperf.

Если хеш-функция имеет нормальное распределение, то вероятность коллизии будет следующей:

для 32 бит: с вероятностью 1 к 10 000 будет коллизия среди 927 хешей, с вероятностью 1 к 100 будет коллизия среди 9 292 хешей,
для 64 бит: с вероятностью 1 к 10 000 будет коллизия среди 60.7 миллионов хешей, с вероятностью 1 к 100 будет коллизия среди 609 миллионов хешей.

Зависимость вероятности коллизии от числа сообщений

На сколько реальны коллизии? Для 32-битных хешей они встречаются регулярно. Например, CRC32 совпадает у «codding» и «gnu», «exhibiters» и «schlager», «завиток» и «естествен» и т.д. Это не вина статистических особенностей хеш-функции, а следствие ограниченного размера хеша — всего 4 байта.

Все перечисленные функции, кроме CRC32 и FNV-1, имеют хорошие статистические показатели. Для 32-битной системы, возможно, быстрее всех будет работать MurmurHash. Если система не может делать невыровненное чтение (unaligned memory read), например, ARM или SPARC, то MurmurHash, в��зможно, также будет работать быстрее всех. Скорость CityHash сильно зависит от компилятора, поскольку используется много сложного кода, она может быть как больше, так и меньше остальных.

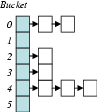
DoS-атака на хеш-таблицу

Можно представить DoS атаку, когда атакующий скармливает в хеш-таблицу данные так, что они попадают все в один слот, и получается худшая скорость поиска одного элемента — O(n), вставки каждой новой коллизии — O(n²), растёт объём памяти (hash-flooding). Для осуществления атаки нужно иметь возможность помещать произвольные данные в хеш-таблицу, и найти коллизии хеш-функции.
Хеш-таблица с коллизиями

Атака ещё называется hash DoS или, более обще, атака на алгоритмическую сложность (algorithmic complexity attack).

Коллизии можно создать несколькими способами:

если хеш-функция заранее известна и длина хеша невелика, то использовать метод перебора: вычисление и поиск в памяти meet-in-the-middle.
если хеш-функция не стойка к коллизиям, то коллизии можно вычислить математически. Некриптографические функции достаточно просты, и для поиска коллизии часто достаточно исполнить алгоритм в обратном порядке ([6], oCERT [7]).

Перечислим свойства криптографических хеш-функций (неприменимо к хеш-функциям общего назначения):

стойкость к восстановлению прообраза (дано m, нельзя найти X так, что H(X) = m),
стойкость к восстановлению второго прообраза (дано m₁, нельзя найти m₂ так, что H(m₁) = H(m₂)),
стойкость к поиску коллизий (нельзя найти m₁ и m₂ так, что H(m₁) = H(m₂)).

Иногда последние два критерия называют стойкостью к коллизиям первого и второго рода соответственно. Мы будем называть коллизией только случай, когда ни сообщение, ни хеш изначально не заданы.

Обычно самая «лёгкая» атака — это поиск коллизий. Из-за парадокса «дней рождений» сложность этой атаки как минимум в два раза меньше, чем длина хеша. Именно эта атака существует для SHA-1: при теоретической сложности коллизии O(2⁸⁰), атака уменьшает сложность до O(2⁶¹). Атаки восстановления первого или второго прообраза для SHA-1 нет.

Чтобы увеличить стойкость к коллизиям, можно:

использовать криптографическую хеш-функцию для вычисления хеша достаточной длины. Она будет стойка к коллизиям, но если коллизии будут однажды вычислены, они смогут быть применены для атаки любой системы.
использовать HMAC (MAC на базе криптографической хеш-функции).
использовать MAC на базе PRF или универсальной хеш-функции (universal one-way hash function).

MAC, построенный на базе криптографической функции, имеет следующие свойства:

нельзя найти ключ, имея возможность получить хеш для любого сообщения,
нельзя найти правильный хеш для сообщения, не зная ключ.
бо́льшая.стойкость к коллизиям, поскольку семейство хеш-функций заранее неизвестно атакующему.

Если мы решим применять криптографическую хеш-функцию (например, SHA-3) или MAC на её основе, то мы столкнёмся со следующими недостатками:

слишком медленно для хеш-таблиц: алгоритм разработан для длинных сообщений, и медленно работает для коротких сообщений,
хотя полная длина хеша устойчива к коллизиям, но если мы возьмём только первые n бит, это упростит поиск коллизий,
в случае HMAC применяются криптографические хеш-функции, которые выполняют лишнюю работу для обеспечения устойчивости к коллизиям, хотя это не нужно, поскольку используется секретный ключ.

Универсальная хеш-функция помимо сообщения также получает ключ, используя который выбирает хеш-функцию из конечного семейства функций. При ключе, известном атакующему, функция должна быть стойка к восстановлению второго прообраза, но нет требования стойкости к коллизиям. Если же ключ неизвестен атакующему, то функция будет стойка к коллизиям. Учитывая наши требования к скорости, желательно обойтись без криптографических функций.

Чтобы усложнить поиск коллизий, иногда пытаются построить MAC на базе хеш-функций общего назначения, используя seed в качестве ключа. Но полученный «MAC» не будет обладать требуемыми свойствами, поскольку построен не на базе криптографической функции. Возможны следующие атаки:

создать коллизии без знания seed, при помощи математического анализа хеш-функции,
выяснить seed, имея доступ к результату хеш-функции (например, программа выдаёт данные, упорядоченные по хешу по умолчанию, это предоставляет утечку данных про значение хеша),
получить данные через timing attack.

Поэтому, хотя этот подход может усложнить жизнь случайному атакующему, часто он не выдерживает простейшего криптоанализа (oCERT [8]). Было показано, что большинство хеш-функций общего назначения не стойки к криптографическим атакам:

xxHash не стойкий к восстановлению второго прообраза даже без знания ключа, зная хеш [12].
MurmurHash 2, MurmurHash 3, CityHash 1.0.3 не стойкие к коллизиям без знания ключа и хеша: был найден способ быстро находить коллизии, которые не зависят от выбора seed («universal» multicollisions) [13].
Python hash не стойкий к восстановлению ключа, зная результат хеш-функции, после чего можно провести атаку против 64-битного состояния с использованием meet-in-the-middle [13].
Python hash не стойкий к коллизиям без знания ключа и хеша [14].

До 2008-2010 года большинство языков и фреймворков использовало достаточно простые хеш-функции:

PHP 4, ASP.NET и JavaScript: DJBX33X,
PHP 5, Ruby 1.8 и Java: DJBX33A,
Rust: DJB (по 2012 год),
Python: модифицированный FNV,
JRuby: MurmurHash2,
Haskell: FNV-1,
Redis: djbhash, позже MurmurHash 2.

Исключение: Perl 4, использовал One-at-a-Time со случайным seed с 2003 года (в этом году обсуждали на конференции эту атаку), позже (5.17.6) использовал MurmurHash 3.

Чтобы уменьшить число коллизий и усложнить DoS атаку, многие языки за последний год перешли на современные хеш-функции со случайным seed. А когда выяснилось, что это не решает проблему с атакой, то многие сменили хеш и во второй раз.

Пример MAC, стойких к коллизиям:

VMAC, UMAC, Poly1305-AES — используют AES-128, оптимальны для длинных сообщений.
SipHash — является PRF, не использует криптографических алгоритмов, оптимальна для коротких сообщений.
“Strongly universal string hashing is fast” [10].

SipHash

2012 год, длина 64 бита, ключ 128 бит.
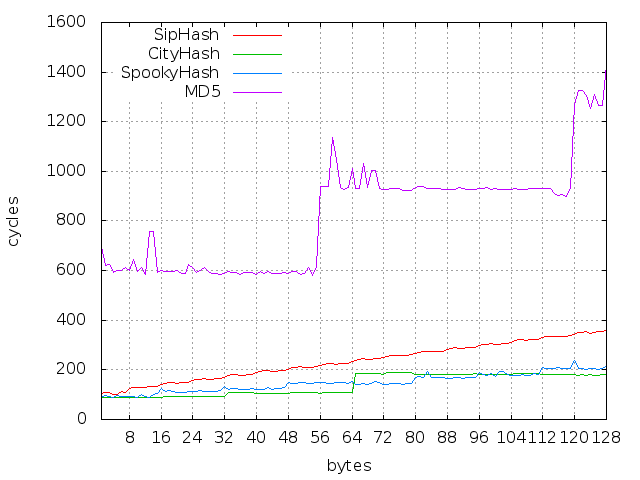
Скорость: 15.50 циклов на байт для 8 байт сообщения, 3.66 циклов на байт для 64 байт сообщения, до 1.96 циклов на байт для длинных сообщений. Для сравнения наиболее быстрый финалист SHA-3 BLAKE-512: 134 цикла на байт для 8 байт, 20 циклов на байт для 64 байт.
Можно использовать любое число раундов compression и finalization. Например, SipHash-2-4 — 2 и 4 раунда соответственно.

Был разработан как не стойкая к коллизиям хеш-функция на основе криптографической псевдослучайной функции (PRF), быстрая для коротких сообщений. Поскольку предполагается использование со случайным ключом, то нет требования стойкости к коллизиям. Отличается от некриптографических хеш-функций тем, что корректно и безопасно работает с ключом, обеспечивая как свойства MAC, так и свойства универсальной хеш-функции.

Зависимость затраченных циклов от длины сообщения

Зависимость затраченных циклов от длины сообщения

Ситуация по языкам на текущий момент выглядит так:

Rust: SipHash 2-4,
Rails: SipHash 2-4,
Perl (5.8.1): SipHash 2-4 (64 бит) и One-at-a-time (32 бит),
Ruby (1.9.3-p327), JRuby: SipHash 2-4,
Python (2.7.3, 3.2.3): собственная хеш-функция, при включении -R добавляется случайный seed [11],
Haskell (1.2): SipHash (для строк),
Go: aeshash (при поддержке AES-NI) или простая собственная функция (вариация FNV-1),
PHP (5): DJBX33A, есть ограничение на количество элементов GET/POST (max_input_vars),
Java SE (7u6 и 8): при включении jdk.map.althashing.threshold используется MurmurHash со случайным seed (alternative string hashing),
Scala: Byteswap32 и MurmurHash 3 или hash от Java,
.NET (4.5): при включении UseRandomizedStringHashAlgorithm используется собственная разработка Marvin32 [9].

Открытые задачи:

Java: нет реакции на криптоанализ MurmurHash [16],
Python: признали, что ключ «-R» бесполезен, и размышляют, как лучше всего исправить атаку на хеш-таблицу [14]
Go: реализовали aeshash, но пока нет криптоанализа [15].

Другие методы защиты

Есть мнение, что борьба с этой атакой — не та задача, которую должна выполнять хеш-функция. Можно вместо этого:

использовать структуры данных с меньшей сложностью в худшем случае. Например, сбалансированное дерево — АВЛ-дерево или красно-чёрное дерево — гарантирует в любом случае O(log n). Здесь важно учитывать новые атаки, например, каскадный ребаланс дерева специально сформированными данными, но даже в этом случае мы получим лучше результат — O(n log n),
ограничить число обрабатываемых элементов (например, POST/GET),
поднимать исключение, если число коллизий больше лимита (или просто отбрасывать данные, если это возможно),
поднимать исключение, если CPU занято больше нормы на операции поиска (timeout).

Некриптографические хеш-функции и DoS атака на них