tguev Aug 5 2013 at 00:00

Об одной изящной конструкции

Medium

7 min

77K

Python*Algorithms*Mathematics*Programming*

Введение

Начну статью с того, что расскажу, как я познакомился с этой изящной конструкцией. Занимаясь олимпиадным программированием, мы с моим преподавателем решали много интересных задач. И вот однажды мне попалась следующая задача:

Распечатать в порядке возрастания все несократимые дроби, знаменатель которых не превосходит заданного числа $n, \, n \le 100$ .

Когда я прочитал условие задачи до конца, она не показалась мне сложной (она таковой и не является). Первое, что пришло мне в голову — это просто перебрать все знаменатели от $inline$ до $inline$ и для каждого знаменателя перебрать числители от $inline$ до знаменателя, при условии, что числитель и знаменатель взаимно просты. Ну, а затем остается отсортировать их по возрастанию.

Такое решение верное, и задача прошла все назначенные ей тесты. Однако мой преподаватель сказал, что задачу можно решить намного красивее. Так я и познакомился с замечательной конструкцией: деревом Штерна — Броко.

Дерево Штерна — Броко

Дерево Штерна — Броко было открыто независимо друг от друга немецким математиком Мерицем Штерном и французским часовщиком Ахиллом Броко. Данное дерево позволяет построить множество всех несократимых неотрицательных дробей.
Для начала введем следующий термин: пусть даны две дроби $\dfrac{x}{y}$ и $\dfrac{z}{t}$ , тогда дробь $\dfrac{x+z}{y+t}$ называется их медиантой.

Построение дерева начнем с двух фиктивных дробей:

$\dfrac{0}{1}$ — обозначающее $inline$
$\dfrac{1}{0}$ — обозначающее бесконечность «в несократимом виде»

На каждой последующей итерации между дробями вставляется их медианта, и эта же операция повторяется для каждой из получившихся пар дробей:

Продолжая данный процесс до бесконечности, мы можем построить все множество несократимых неотрицательных дробей.

Дерево Штерна — Броко не было бы столь интересным, если бы не его замечательные особенности (а их у него немало):

несократимость дробей
упорядоченность дробей
наличие абсолютно всех дробей

Можно задаться вопросами: почему все дроби несократимы? Почему упорядочены? Почему ни одна дробь не может встретиться более чем один раз? Ответы на эти вопросы достаточно просты. Нужно лишь немного подробнее рассмотреть структуру этого дерева.

Пусть $\dfrac{x}{y}$ и $\dfrac{z}{t}$ — две последовательные дроби дерева Штерна — Броко. Можно заметить, что для них выполняется равенство $inline$ (проверьте это сами для нескольких пар дробей). Докажем данное утверждение по индукции для всех дробей в дереве. За базу индукции примем дроби $\dfrac{0}{1}$ и $\dfrac{1}{0}$ , для которых верно равенство $1\cdot 1 - 0\cdot 0 = 1$ .

Теперь покажем, что при вставке медианты между дробями $\dfrac{x}{y}$ и $\dfrac{z}{t}$ , для которых равенство $inline$ верно, оно также будет выполняться и для дробей $\dfrac{x}{y}, \dfrac{x+z}{y+t}$ и $\dfrac{x+z}{y+t}, \dfrac{z}{t}$ .
Имеем:

$y(x+z)-x(y+t) = 1 \iff yz-xt = 1\\ z(y+t) - t(x+z) = 1 \iff zy - tx = 1$

Как видите, оба этих уравнения эквивалентны исходному, поэтому условие $inline$ является инвариантом для всех последовательных дробей в дереве. Условие $inline$ означает, что $\mathrm{GCD}(x, y) = \mathrm{GCD}(z, t) = 1$ , то есть числа $inline$ и $inline$ взаимно просты.

Вот почему дроби несократимы — числитель и знаменатель всегда взаимно просты. На первый вопрос ответили! Переходим ко второму.

Почему дроби будут упорядочены? Для ответа на этот вопрос достаточно показать, что медианта двух дробей всегда лежит между ними.

Пусть $\dfrac{x}{y}$ и $\dfrac{z}{t}$ — две последовательные дроби в дереве и $\dfrac{x}{y} \le \dfrac{z}{t}$ . Покажем, что $\dfrac{x}{y} \le \dfrac{x+z}{y+t} \le \dfrac{z}{t}$ . Приводя дроби к общему знаменателю и учитывая условие $\dfrac{x}{y} \leq \dfrac{z}{t} \iff xt-yz \leq 0$ , получаем:

$\dfrac{x(y+t)-y(x+z)}{y(y+t)} \leq 0 \iff \dfrac{xt-yz}{y(y+t)} \leq 0 \\ \dfrac{t(x+z)-z(y+t)}{t(y+t)} \leq 0 \iff \dfrac{xt-y z}{t(y+t)} \leq 0$

Учитывая, что знаменатели у последних дробей положительные, числители должны быть отрицательными, а это и есть исходное неравенство $xt - yz \leq 0$ . Отсюда делаем вывод, что медианта двух дробей всегда расположена между ними (но необязательно посередине). Тем самым мы показали упорядоченность дробей в дереве Штерна — Броко.

Ну и последнее: почему мы не можем пропустить хотя бы одну дробь, то есть почему все дроби присутствуют в дереве?

Если бы нам надо было найти определенную дробь в дереве, то как бы мы это сделали? Процесс поиска фактически является бинарным поиском. Мы сравниваем искомую дробь с медиантой, и возможны $inline$ случая:

она равна медианте, поиск завершен
медианта больше дроби, тогда рекурсивно отправляемся искать в левое поддерево
медианта меньше дроби, тогда рекурсивно отправляемся искать в правое поддерево

Очевидно, этот процесс не может выполняться бесконечно долго, то есть когда-нибудь мы найдем нашу дробь (додумайте сами, почему это так).

Последовательность Фарея

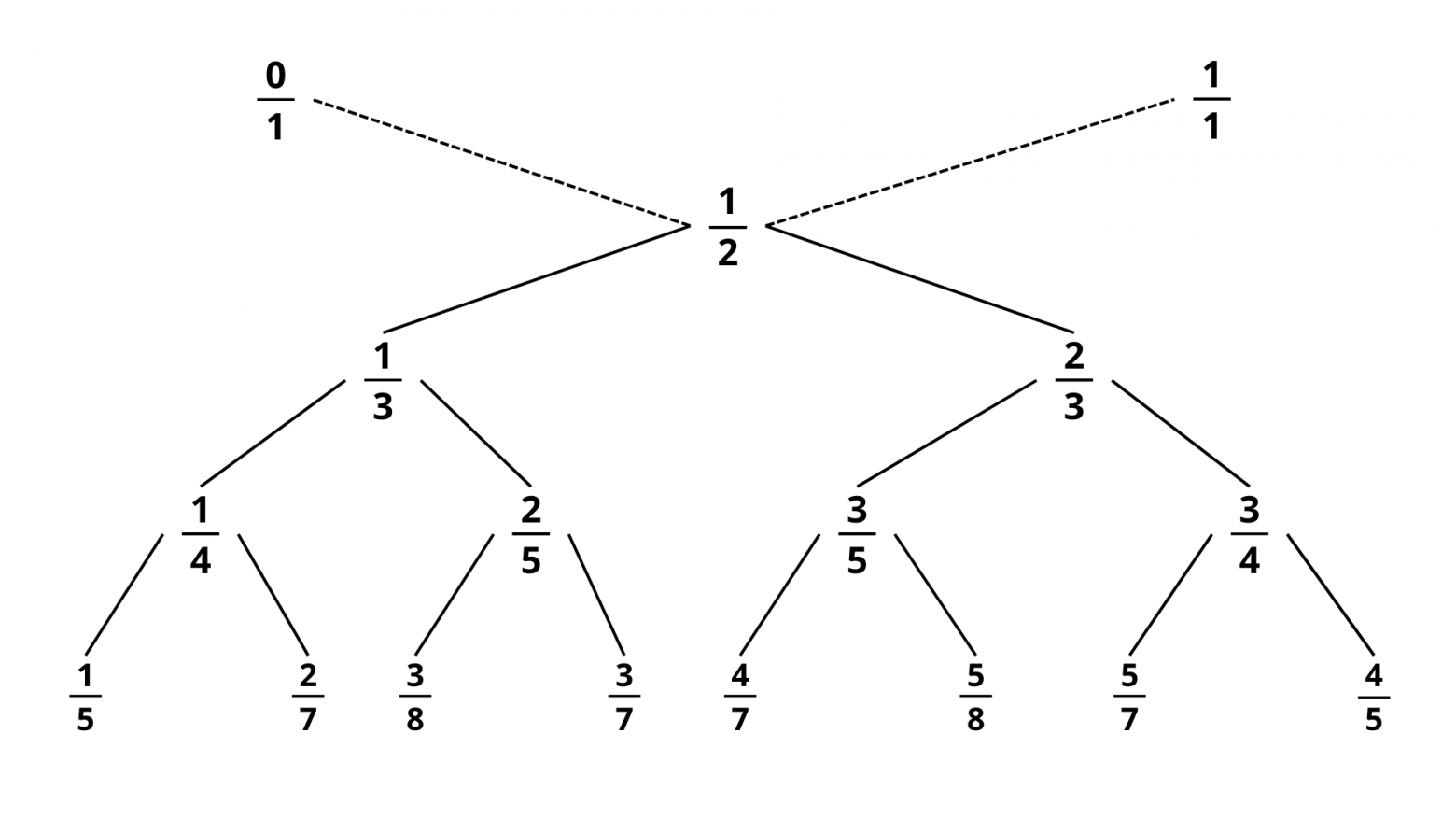Ну а что же с исходной задачей? Вроде бы дерево Штерна — Броко нам подходит, но в нем есть дроби большие единицы, которые являются лишними. Однако что нам мешает взять вместо фиктивных дробей $\dfrac{0}{1}$ и $\dfrac{1}{0}$ дроби $\dfrac{0}{1}$ и $\dfrac{1}{1}$ ? Ничего!

Такой частный случай дерева Штерна — Броко является основой для последовательности Фарея. Последовательность Фарея порядка $inline$ является множество всех несократимых дробей между $inline$ и $inline$ , знаменатель которых не превосходит $inline$ , которые расположены в порядке возрастания. Обозначается последовательность буквой $inline$ .

Строго математически эту последовательность можно записать так:

$F_n=\left\{\frac{a_i}{b_i}: 0 \leq a_i \leq b_i \leq n, \operatorname{GCD}\left(a_i, b_i\right)=1, \frac{a_i}{b_i} \leq \frac{a_{i+1}}{b_{i+1}}\right\}$

Так выглядит последовательность Фарея для $n = 1,\ldots,5$ :

$F_1=\left\{\frac{0}{1}, \frac{1}{1}\right\}, F_2=\left\{\frac{0}{1}, \frac{1}{2}, \frac{1}{1}\right\}, F_3=\left\{\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1}\right\} \\ F_4=\left\{\frac{0}{1}, \frac{1}{4}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{1}{1}\right\}, F_5=\left\{\frac{0}{1}, \frac{1}{5}, \frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{3}{5}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{1}{1}\right\}$

Последовательность названа в честь Джона Фарея — известного геолога.

Фактически исходную задачу можно переформулировать следующим образом: построить последовательность Фарея $inline$ -порядка. Код на языке Python для ее построения выглядит очень просто, всего два рекурсивных вызова:

def farei_sequence(n):
    result = ['0/1']
    def farei_sequence_rec(n, x, y, z, t):
        a, b = x + z, y + t
        if b <= n:
            farei_sequence_rec(n, x, y, a, b)
            result.append(f'{a}/{b}')
            farei_sequence_rec(n, a, b, z, t)
      
    farei_sequence_rec(n, 0, 1, 1, 1)
    result.append('1/1')
    return result

print(*farei_sequence(3))    # 0/1 1/3 1/2 2/3 1/1
print(*farei_sequence(4))    # 0/1 1/4 1/3 1/2 2/3 3/4 1/1
print(*farei_sequence(5))    # 0/1 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1/1
print(*farei_sequence(6))    # 0/1 1/6 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 5/6 1/1

Дроби Фарея также можно использовать при упрощении математических выражений.

Например, требуется посчитать выражение $\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}$ .

Стандартный способ приведения к общему знаменателю нам неинтересен. Представим дроби в виде разности соседних дробей ряда Фарея:

$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}=1-\frac{1}{10}=\frac{9}{10}$

Вот так просто можно посчитать это выражение! На этом покончим с последовательностью Фарея и еще раз вернемся к дереву Штерна — Броко.

Дерево как система счисления

Оказывается, дерево Штерна — Броко можно использовать в качестве системы счисления (символического способа) для представления рациональных чисел.

Но как сопоставить с каждой дробью некоторую последовательность символов? Для этого еще раз вспомним алгоритм поиска определенной дроби в дереве.

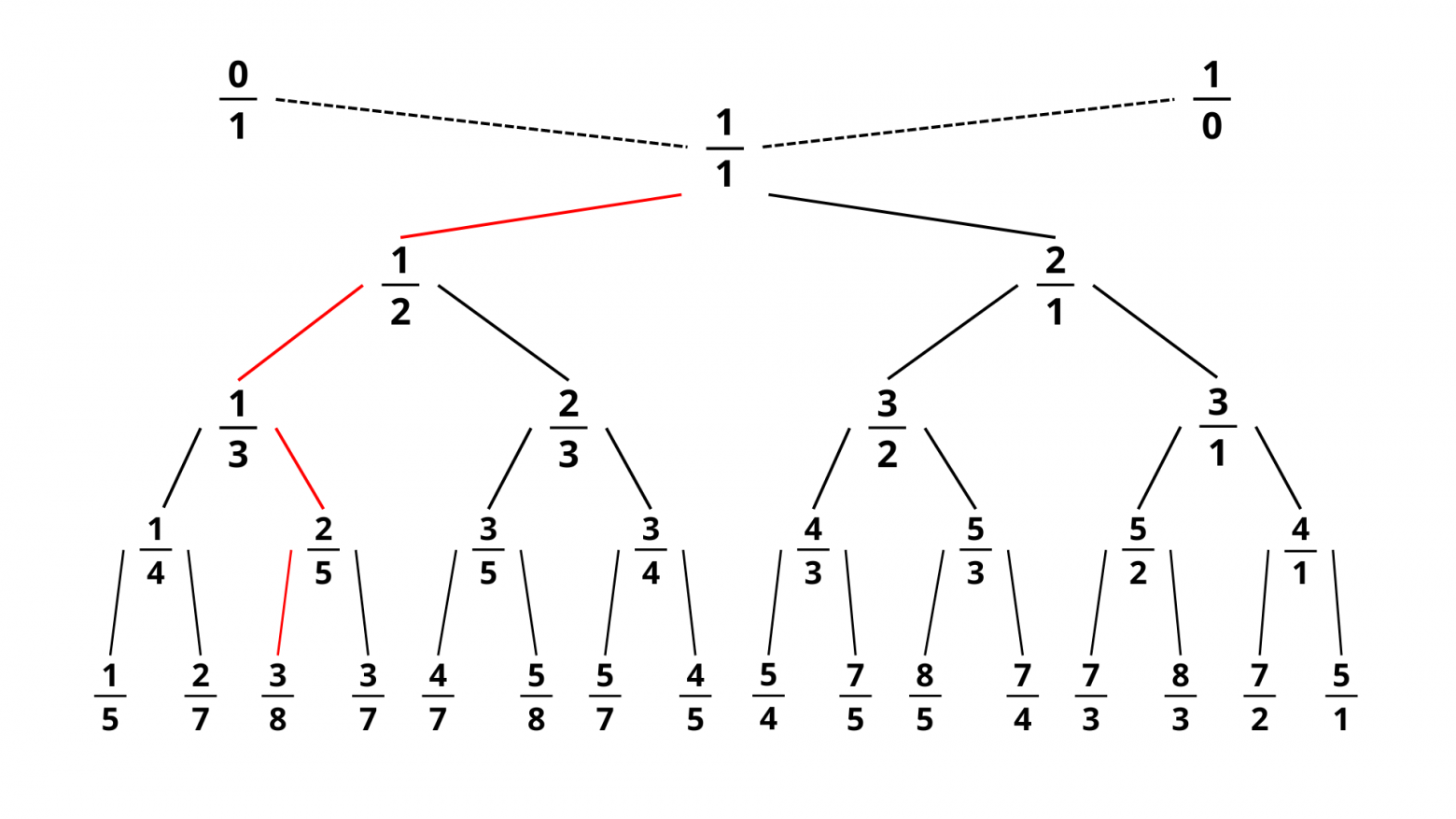Пусть нам надо найти дробь $\dfrac{3}{8}$ в дереве. Начинаем поиск с медианты $\dfrac{1}{1}$ . Переход по левому поддереву обозначим буквой L, по правому поддереву — буквой R. Таким образом, числу $\dfrac{3}{8}$ соответствует последовательность символов LLRL (см. рисунок).

Таким образом, мы можем каждой рациональной дроби поставить в соответствие последовательность букв L И R (или же вовсе можем заменить их на $inline$ и $inline$ для полного соответствия двоичной системе счисления).

Приближение действительных чисел рациональными

Если в процессе поиска дроби в дереве Штерна-Броко вместо дроби передать действительное число, то можно получить его приближение рациональными дробями. Попробуем приблизить число $\pi$ . Получим такой результат: RRRLLLLLLLRRRRRRRRRRRRRRRLRRRR.....

Исходя из этого представления, можно предположить, что дроби

$\begin{array}{ccccccccccccccccccccccccccc} \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{L} & \mathrm{L} & \mathrm{L} & \mathrm{L} & \mathrm{L} & \mathrm{L} & \mathrm{L} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{R} & \mathrm{L} \\ \frac{1}{1} & \frac{2}{1} & \frac{3}{1} & \frac{4}{1} & \frac{7}{2} & \frac{10}{3} & \frac{13}{4} & \frac{16}{5} & \frac{19}{6} & \frac{22}{7} & \frac{25}{8} & \frac{47}{15} & \frac{69}{22} & \frac{91}{29} & \frac{113}{36} & \frac{135}{43} & \frac{157}{50} & \frac{179}{57} & \frac{201}{64} & \frac{223}{71} & \frac{245}{78} & \frac{267}{85} & \frac{289}{92} & \frac{311}{99} & \frac{333}{106} & \frac{355}{113} \end{array}$

служат простейшими рациональными приближениями к числу $\pi$ сверху и снизу. Таким образом, можно заключить, что $\dfrac{333}{106}<\pi<\dfrac{355}{113}$ .

? Если статья оказалась интересной и полезной для вас, подписывайтесь на телеграм-канал «Поколение Python ?», который я веду вместе со своей командой.

Hubs: