Добрый день, уважаемые хабропользователи.
Хотел бы поделиться практическим применением одного из алгоритмов нейродинамики, в продолжении моего поста Моделирование нейросети Машина Больцмана.
Реализация на примере решения задачи коммивояжера.
Немного напомню в чем ее суть.

Задача коммивояжера (коммивояжер (фр. commis voyageur, устар.) — разъездной сбытовой посредник) заключается в нахождении самого выгодного маршрута, проходящего через указанные города. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешевый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.
Для решения данной задачи используется сеть, состоящая из 100 нейронов.
При присвоении весов должна существовать гарантия, что нейросеть предоставляет решение, которое соответствует корректному туру. Становится ясно, почему присвоение весов является наиболее значительным для достижения хорошего решения при использовании машины Больцмана и сети Хопфилда. Хопфилд и Танк предложили один путь присвоения весов для машин Больцмана. Основной идеей является наложение штрафов на некорректные туры и в то же время минимизация длины тура. Подход Aarts дает возможность формально установить присвоения, связав с поставленной задачей, тогда как многие другие подходы для присвоения весов являются эвристическими. Конечно, необязательно подразумевается, что результирующий алгоритм работает хорошо, поэтому Aarts предлагает несколько модификаций, предназначенные для улучшения производительности больших задач.

Рис.14 Рис. 15
Рисунки (14) и (15) иллюстрируют соединения сделанные к каждому узлу сети. Они разделены на два типа. Соединения расстояний, для которых веса выбраны таким образом, что если сеть находится в состоянии которое соответствует туру, эти веса будут отражать стоимость энергии соединения (p-1) города тура с p городом, а p – город с городом (p+1).
На рисуноке (14) изображены соединения расстояний. У каждого узла (i, p) есть запрещающие связи к двум смежным колонкам, чьи веса отражают стоимость соединения трёх городов.
Рисунок (15) отображает исключающие соединения. У каждого узла (i, p) есть запрещающие связи ко всем элементам в том же ряду и колонке.
Исключающие соединения запрещают двум элементам находиться в одном и том же ряду или колонке в одно и то же время. Исключающие соединения позволяет сети установиться в состояние соответствующем состоянию тура.
Так как все соединения до настоящего времени запрещающие, мы должны предоставить сети некоторый стимул для включения элементов, при помощи манипулирования порогами. Интуитивно мы можем видеть, что некоторые расположения, такие как изображенные на рисунках (14) и (15), могут обладать требуемым эффектом, но следующая теорема показывает как точно выбрать веса. Рассмотрим следующий набор параметров:
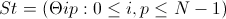
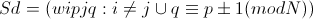
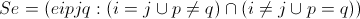
(13)
Где, dij – это расстояние между i и j городами, N – количество городов, eipjq – энергия между нейронами (j, q) и (i, p).
Заметим, что каждый элемент на рисунках (14) и (15) находится в таблице, следовательно какой либо особенный элемент идентифицируется двумя подписями. θip является входом элемента (i, p), а wipjq вес от элемента (j, q) к (i, p).
Выберем веса и входы таким образом чтобы
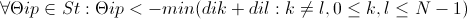
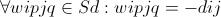
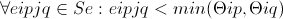
(14)
Тогда
1. Выполнимость. Корректные состояния туров сети точно соотносится с локальным минимумом энергии
2. Упорядочение. Функция энергии является порядкосберегающей в соответствии с длиной тура.
Доказательство довольно прямолинейно и зависит от демонстрации, что состояния туров абсолютно точно соотносятся с локальным минимумом энергии. В асинхронной машине Больцмана локальным минимумы энергий совершенно точно соотносятся с фиксированными точками. Недостатком алгоритма является то, что в синхронном случае некоторые локальные минимумы энергий могут также соответствовать двум циклам, что усложняет присвоение весов в синхронном случае.
При решении задачи коммивояжера функционирование сети выглядит следующим образом:
1. Рассчитываются весы, с учетом поставленной задачи, по алгоритму описанному выше.
2. Подается на вход сигнал
3. Производится активация нейронов по алгоритму обучения Больцмана, за исключением того, что веса остаются всегда одинаковыми.
4. Повторяются действия 2 и 3 до тех пор, пока энергия не попадет в глобальный минимум (т.е. в течении n вычислений не изменяет свое состояние).
Оптимизация работы алгоритма
Решая задачу при помощи алгоритма «Имитации отжига» помимо правильного подбора весов, входного вектора, пороговых значений и размерности, не менее важен параметр t (температура).
Металл отжигают, нагревая его до температуры, превышающей точку его плавления, а затем давая ему медленно остыть. При высоких температурах атомы, обладая высокими энергиями и свободой перемещения, случайным образом принимают все возможные конфигурации. При постепенном снижении температуры энергии атомов уменьшаются, и система в целом стремится принять конфигурацию с минимальной энергией. Когда охлаждение завершено, достигается состояние глобального минимума энергии.
При фиксированной температуре распределение энергий системы определяется вероятностным фактором Больцмана
Отсюда очевидно: имеется конечная вероятность того, что система обладает высокой энергией даже при низких температурах. Сходным образом имеется небольшая, но вычисляемая вероятность, что чайник с водой на огне замерзнет, прежде чем закипит.
Статистическое распределение энергий позволяет системе выходить из локальных минимумов энергии. В то же время, вероятность высокоэнергетических состояний быстро уменьшается со снижением температуры. Следовательно, при низких температурах имеется сильная тенденция занять низкоэнергетическое состояние.
Для более гибкого изменения температуры весь график был разбит на интервалы, в которых пользователь может сам менять скорость падения температуры (до 50 итераций, от 50 до 120 итераций, более 120 итераций).
В процессе практических исследований были выведены следующие закономерности:
1. При высоких температурах энергия ведет себя хаотично, когда при низких температурах становится практически детерминированной.
2. Изменяя температуру на любую константу в любом интервале, чаще всего алгоритм находит путь между всеми городами, однако по большей мере далекий от оптимального.
3. Для получения наиболее точного ответа необходимо на низких температурах значительно уменьшать скорость падения параметра t, чего нельзя сказать про высокие температуры. Когда температура максимальная, скорость падения практически никак не влияет на результат.
В процессе данных исследований мы выявили, что температура имеет куда большее значение, чем любой другой параметр, участвующий в вычислениях, для достижения наиболее точного результата (в данном случае наименьшего пути между городами). Достигнуть этого можно путем снижения темпов падения параметра t на завершающем участке вычислений. В используемой нами модели сети снижение рекомендуется производить на интервале «после 120 итераций».
Для наглядного изображения полученных результатов в разработанной нами программе, моделирующей сеть, приводится график температуры, при котором был достигнут оптимальный результат.

Так же произведены исследования в области активации нейросети. Помимо стандартного изменения состония в отдельности каждого нейрона, выбранного случайным образом, активация производится группы нейронов (в данной модели в группу входит 10 нейронов). Каждый нейрон в этой группе меняет свое состояние на противоположенное. Такой способ активации позволяет еще больше распараллелить процесс вычислений, что приводит к более быстрому нахождению верного решения. Количество шагов вычисления сократилось с 534 до 328.
Таким образом данную нейросеть возможно оптимизировать не только относительно точности, изменяя график температуры, но и скорость нахождения верного ответа, путем увеличения количества нейронов, изменяющих свое состояние в один момент времени.
Хотел бы поделиться практическим применением одного из алгоритмов нейродинамики, в продолжении моего поста Моделирование нейросети Машина Больцмана.
Реализация на примере решения задачи коммивояжера.
Немного напомню в чем ее суть.

Задача коммивояжера (коммивояжер (фр. commis voyageur, устар.) — разъездной сбытовой посредник) заключается в нахождении самого выгодного маршрута, проходящего через указанные города. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешевый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.
Для решения данной задачи используется сеть, состоящая из 100 нейронов.
При присвоении весов должна существовать гарантия, что нейросеть предоставляет решение, которое соответствует корректному туру. Становится ясно, почему присвоение весов является наиболее значительным для достижения хорошего решения при использовании машины Больцмана и сети Хопфилда. Хопфилд и Танк предложили один путь присвоения весов для машин Больцмана. Основной идеей является наложение штрафов на некорректные туры и в то же время минимизация длины тура. Подход Aarts дает возможность формально установить присвоения, связав с поставленной задачей, тогда как многие другие подходы для присвоения весов являются эвристическими. Конечно, необязательно подразумевается, что результирующий алгоритм работает хорошо, поэтому Aarts предлагает несколько модификаций, предназначенные для улучшения производительности больших задач.

Рис.14 Рис. 15
Рисунки (14) и (15) иллюстрируют соединения сделанные к каждому узлу сети. Они разделены на два типа. Соединения расстояний, для которых веса выбраны таким образом, что если сеть находится в состоянии которое соответствует туру, эти веса будут отражать стоимость энергии соединения (p-1) города тура с p городом, а p – город с городом (p+1).
На рисуноке (14) изображены соединения расстояний. У каждого узла (i, p) есть запрещающие связи к двум смежным колонкам, чьи веса отражают стоимость соединения трёх городов.
Рисунок (15) отображает исключающие соединения. У каждого узла (i, p) есть запрещающие связи ко всем элементам в том же ряду и колонке.
Исключающие соединения запрещают двум элементам находиться в одном и том же ряду или колонке в одно и то же время. Исключающие соединения позволяет сети установиться в состояние соответствующем состоянию тура.
Так как все соединения до настоящего времени запрещающие, мы должны предоставить сети некоторый стимул для включения элементов, при помощи манипулирования порогами. Интуитивно мы можем видеть, что некоторые расположения, такие как изображенные на рисунках (14) и (15), могут обладать требуемым эффектом, но следующая теорема показывает как точно выбрать веса. Рассмотрим следующий набор параметров:
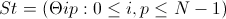
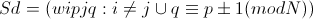
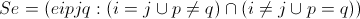
(13)
Где, dij – это расстояние между i и j городами, N – количество городов, eipjq – энергия между нейронами (j, q) и (i, p).
Заметим, что каждый элемент на рисунках (14) и (15) находится в таблице, следовательно какой либо особенный элемент идентифицируется двумя подписями. θip является входом элемента (i, p), а wipjq вес от элемента (j, q) к (i, p).
Выберем веса и входы таким образом чтобы
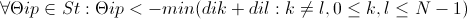
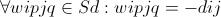
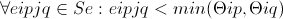
(14)
Тогда
1. Выполнимость. Корректные состояния туров сети точно соотносится с локальным минимумом энергии
2. Упорядочение. Функция энергии является порядкосберегающей в соответствии с длиной тура.
Доказательство довольно прямолинейно и зависит от демонстрации, что состояния туров абсолютно точно соотносятся с локальным минимумом энергии. В асинхронной машине Больцмана локальным минимумы энергий совершенно точно соотносятся с фиксированными точками. Недостатком алгоритма является то, что в синхронном случае некоторые локальные минимумы энергий могут также соответствовать двум циклам, что усложняет присвоение весов в синхронном случае.
При решении задачи коммивояжера функционирование сети выглядит следующим образом:
1. Рассчитываются весы, с учетом поставленной задачи, по алгоритму описанному выше.
2. Подается на вход сигнал
3. Производится активация нейронов по алгоритму обучения Больцмана, за исключением того, что веса остаются всегда одинаковыми.
4. Повторяются действия 2 и 3 до тех пор, пока энергия не попадет в глобальный минимум (т.е. в течении n вычислений не изменяет свое состояние).
Оптимизация работы алгоритма
Решая задачу при помощи алгоритма «Имитации отжига» помимо правильного подбора весов, входного вектора, пороговых значений и размерности, не менее важен параметр t (температура).
Металл отжигают, нагревая его до температуры, превышающей точку его плавления, а затем давая ему медленно остыть. При высоких температурах атомы, обладая высокими энергиями и свободой перемещения, случайным образом принимают все возможные конфигурации. При постепенном снижении температуры энергии атомов уменьшаются, и система в целом стремится принять конфигурацию с минимальной энергией. Когда охлаждение завершено, достигается состояние глобального минимума энергии.
При фиксированной температуре распределение энергий системы определяется вероятностным фактором Больцмана
Отсюда очевидно: имеется конечная вероятность того, что система обладает высокой энергией даже при низких температурах. Сходным образом имеется небольшая, но вычисляемая вероятность, что чайник с водой на огне замерзнет, прежде чем закипит.
Статистическое распределение энергий позволяет системе выходить из локальных минимумов энергии. В то же время, вероятность высокоэнергетических состояний быстро уменьшается со снижением температуры. Следовательно, при низких температурах имеется сильная тенденция занять низкоэнергетическое состояние.
Для более гибкого изменения температуры весь график был разбит на интервалы, в которых пользователь может сам менять скорость падения температуры (до 50 итераций, от 50 до 120 итераций, более 120 итераций).
В процессе практических исследований были выведены следующие закономерности:
1. При высоких температурах энергия ведет себя хаотично, когда при низких температурах становится практически детерминированной.
2. Изменяя температуру на любую константу в любом интервале, чаще всего алгоритм находит путь между всеми городами, однако по большей мере далекий от оптимального.
3. Для получения наиболее точного ответа необходимо на низких температурах значительно уменьшать скорость падения параметра t, чего нельзя сказать про высокие температуры. Когда температура максимальная, скорость падения практически никак не влияет на результат.
В процессе данных исследований мы выявили, что температура имеет куда большее значение, чем любой другой параметр, участвующий в вычислениях, для достижения наиболее точного результата (в данном случае наименьшего пути между городами). Достигнуть этого можно путем снижения темпов падения параметра t на завершающем участке вычислений. В используемой нами модели сети снижение рекомендуется производить на интервале «после 120 итераций».
Для наглядного изображения полученных результатов в разработанной нами программе, моделирующей сеть, приводится график температуры, при котором был достигнут оптимальный результат.

Так же произведены исследования в области активации нейросети. Помимо стандартного изменения состония в отдельности каждого нейрона, выбранного случайным образом, активация производится группы нейронов (в данной модели в группу входит 10 нейронов). Каждый нейрон в этой группе меняет свое состояние на противоположенное. Такой способ активации позволяет еще больше распараллелить процесс вычислений, что приводит к более быстрому нахождению верного решения. Количество шагов вычисления сократилось с 534 до 328.
Таким образом данную нейросеть возможно оптимизировать не только относительно точности, изменяя график температуры, но и скорость нахождения верного ответа, путем увеличения количества нейронов, изменяющих свое состояние в один момент времени.