CFD 3D: простой симулятор воды / Habr

Введение

CFD (Computational fluid dynamics) — вычислительная гидродинамика.
Используется для моделирования разных процессов в жидкостях, а также разных типов жидкостей (например мёд, нефть — это все жидкости).

В данном посте рассматривается 2D симулятор обычной воды с открытой поверхностью и препятствиями (для 3D версии все аналогично + доступны исходники).
Поверхность воды представляет собой границу, отделяющую воду от воздуха.Это позволяет моделировать волны, падение капель и т.д.

Написать свой симулятор я решил по нескольким причинам. Одна из них — это отсутствие нормально написанных исходников по данной теме в интернете. Все что я находил, было или на фортране, или только 2d, или написано очень сложно для понимания.

Итак, основные фичи симулятора:

real-time режим
простая и понятная схема расчета + explicit, implicit
открытый исходный код
есть и 2d и 3d
встроенный простой opengl render
xml описание сцен

В плане расчетов я отталкивался от уравнений Навье-Стокса (а также от найденных в инете исходников).
Это система дифференциальных уравнений в частных производных, описывающая движение вязкой несжи��аемой жидкости. Слово несжимаемой здесь скорее для галочки, поскольку все жидкости по определению являются несжимаемыми. Вязкость обозначает трение между отдельными частицами, она не дает разлетаться им в разных направлениях как в случае с газом, когда он заполняет весь отведенный ему объем. Частицы жидкости же стараются держатся по возможности вместе.

В своем симуляторе я использовал немного измененный набор уравнений, об этом ниже…

Уравнения гидродинамики

Итак, вот основные уравнения Навье-Стокса в общем (векторном) виде:

Здесь:

u — это традиционное обозначение поля скорости ( в 2D — скорость состоит из 2-х компонент по x и по y направлениям — обозначаются они соответственно как u и v)
p — это давление
t — время
символ rho — плотность жидкости
символ nu — кинематический коэффициент вязкости
Fext — какие-либо внешние силы действующие на жидкость, например гравитация ( g )

Первое из уравнений — уравнение движения, второе — уравнение неразрывности.
Уравнение движения выглядит похожим на уравнение Ньютона ma=F, где у нас справа — сумма сил действующих на жидкость — это давление, диффузия, гравитация…

Для 2D варианта уравнения принимают такой вид (здесь уже они представлены в безразмерном виде):

Уравнение движения теперь представлено 2 уравнениями — для 2х компонентов скорости — u и v.
По поводу нового коэффициента Re — это число Рейнольдса (оно получилось при переходе к безразмерным переменным), которое заменяет сразу 2 предыдущих коэффициента — коэфф. плотности и вязкости. От него зависит на что будет похожа вода — на мед или на обычную воду. Чем больше Re тем более похожа жидкость на обычную воду.
В скобках это у нас выражение определяющее вязкое поведение жидкости (или диффузия). Остальные члены в правой части (кроме гравитации) — это конвекция. В левой части — скорость и давление.

Далее я немного упростил эти уравнения:

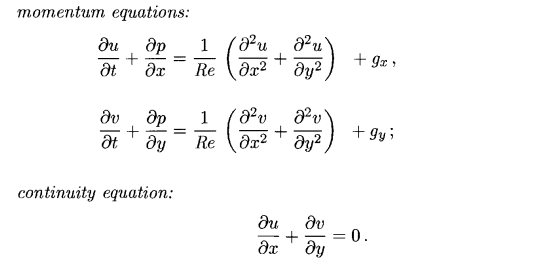
Как видно — исчезла конвекция, что несколько ухудшает поведение жидкости, но в целом визуально выглядит вполне нормально.Отсутствие конвекции дает сразу несколько плюсов — исчезает нелинейность, улучшается стабильность и шаг по времени можно делать больше, также конвекция обычно очень затратный терм по количеству необходимых вычислений, к тому же чтобы правильно дискретизировать конвекцию- применяют специальные схемы — что выглядит достаточно громоздко.

При решении уравнений применяется специальная схема, называемая Splitting.Очень хотелось бы остановиться поподробней на этом, но это скорее для отдельного поста.Тема достаточно большая.Очень хорошо это описано в книге
Bridson R. Fluid Simulation for Computer Graphics.pdf в разделе Overview of numerical simulation.
И тут Numerical simulation in fluid dynamics Griebel M Dornseifer T Neunhoeffer T SIAM 1998

Вот split схема решения уравнений:

Для шага по времени используется метод Эйлера, также на первом шаге мы опускаем давление и получаем промежуточный расчет скоростей F и G. Эти скорости, кроме того что не учитывают давление, еще и не будут удовлетворять уравнению неразрывности. Путем хитрых манипуляций находится уравнение для расчета давления, которое в том числе решает и проблему с уравнением неразрывности. Решая это уравнение по уже рассчитанным F и G мы находим новое давление P.
Далее на 3-м шаге происходит коррекция скоростей с учетом посчитанного давления.
На этом завершается один полный шаг по времени и на следующем шаге все повторяется заново.

Дискретизация уравнений

Для дискретизации уравнений используется метод конечных разностей. Для шага по времени используется стандартный метод Эйлера — схематично выглядит это так: u(n+1)=u(n) + dt* f,
где под f понимается вся часть уравнения в которую не входит дифференциал по времени.

В общем значение скорости в новый момент времени ( u(n+1) ) находим из значения в предыдущий момент времени ( u(n) ).
Описывать дискретные аналоги уравнений в данном посте я не буду.Это очень хорошо сделано в книге «Numerical simulation in fluid dynamics» (Griebel M Dornseifer T Neunhoeffer T SIAM 1998).

Для решения дискретных уравнений используется не матричный способ решения а итеративный — Гаусс-Зейделя. Он не требует предварительной сборки матриц и вообще не требует никаких промежуточных массивов, позволяет легко модифицировать расчетную схему, приблизительное решение находиться уже через 1 итерацию — что очень ускоряет всю симуляцию.

В данном посте будет рассмотрен 2D случай, основной акцент будет на объяснении граничных условий, т.к. они вызывают наибольшие сложности в решении уравнений. Вся симулируемая область разбивается на imax точек по горизонтали и jmax по вертикали. Получается сетка imax*jmax клеток.
К ним с 4 границ добавляются граничные точки. Итого получается массив размером (imax+2)*(jmax+2).

У каждой клетки свои значения скоростей и давления — принято говорить о векторном поле скоростей и скалярном поле давления на расчетной сетке.
U — скорость частицы в клетке по x
V — скорость частицы в клетке по y
P — давление

Обычно принято располагать расчетные переменные (U,V,P) по центру клеток, но в случае с моделированием жидкости это всегда вызывает проблемы с решением — оно получается не совсем корректное и осциллирующее. Поэтому в CFD используется разнесенная сетка (staggered grid) — еще ее называют чехарда.

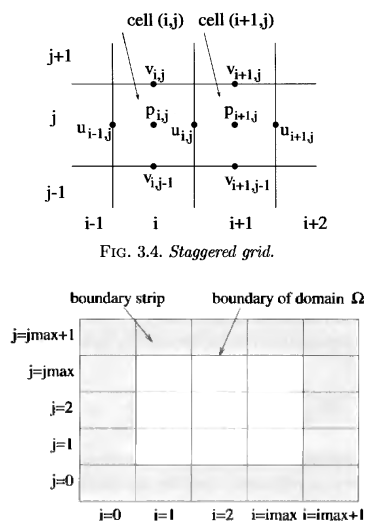
Из рисунка видно что скорости находятся не в самой клетке а на ее гранях, u — на правой границе клетки, а v — на верхней границе.

Граничные условия на стенках

Для расчета методом конечных разностей, нам нужно задать значения (u,v,p) на границах раcчетной сетки.Это 4 стенки — слева справа снизу и сверху.Граничные условия могут быть типов no-slip и free-sleep; есть и другие типы, но это скорее специализированные условия, а не общего плана.

free-sleep — это значит что жидкость свободно скользит по стенке, как будто отсутствует трение и ничто ей не мешает двигаться вдоль неё.
В данном посте мы не рассматриваем этот тип граничных условий.

no-slip — это условие прилипания — то есть жидкость притормаживает когда натыкается на стенку.
Это означает, что скорость жидкости совпадает со скоростью стенки (то есть в нашем случае равна нулю на неподвижной границе).

Рассмотрим для примера только правую границу: u составляющая скорости = 0, т.к. она перпендикулярна стенке и вода не должна проникать сквозь границу.
v составляющая для случая no-slip границы тоже равна 0, но для нашей staggered сетки придется ее скорректировать.Для v составляющей, учитывая что v не находится прямо на границе, необходимо немного подправить выражение.
v на стенке будет равно среднему между 2-я последними ячейками. v_g=(v[imax+1][j]+v[imax][j])/2
v_g приравняем нулю ( (v[imax+1][j]+v[imax][j])/2=0 ) и найдем отсюда значение v[imax+1][j], которое нам и нужно задать в программе:
v[imax+1][j]=-v[imax][j];
Тоже самое необходимо проделать для u компоненты на верхней границе.

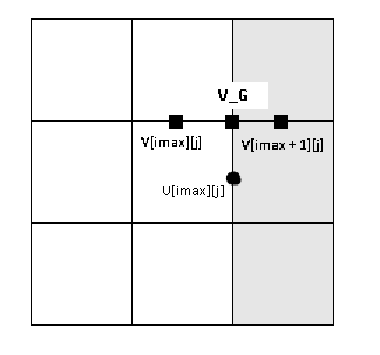
4 границы представлены в массиве следующими координатами:

левая стенка

u[0][j], где j пробегает значения по всей стенке
v[0][j]

Вот как это выглядит в коде:

for (j = 0; j <= jmax + 1; j++)
{
  U[0][j] = 0.0;
  V[0][j] = -V[1][j];
}

нижняя стенка

u[i][0]
v[i][0]

for (i = 0; i <= imax + 1; i++)
{
  U[i][0] = -U[i][1];
  V[i][0] = 0.0;
}

правая стенка
Т.к у нас разнесенная сетка, то на правой стенке у нас граница для значений u проходит не по последнему столбцу а по предпоследнему — поэтому ставим значения для U в клетке — U[imax][j].

u[imax][j]
v[imax+1][j]

for (j = 0; j <= jmax + 1; j++)
{
  U[imax][j] = 0.0;
  V[imax + 1][j] = -V[imax][j];
}

верхняя стенка
Здесь уже для значений v граница проходит по предпоследней строке — jmax — поэтому ставим значения для V в клетке — V[i][jmax]

u[i][jmax+1]
v[i][jmax]

for (i = 0; i <= imax + 1; i++)
{
  U[i][jmax + 1] = -U[i][jmax];
  V[i][jmax] = 0.0;
}

Для тестирования основного решателя можно все граничные значения задать =0.

Также нам нужно проставить давление на границах.Давление задано по центру клеток а не по краям как скорости.Поэтому с ним все очень просто.Давление на границах можно поставить таким же как и в соседних клетках.Просто копируем значения из соседних клеток.

for (j = 1; j <= jmax; j++)
{
  // левая стенка
  P[0][j] = P[1][j];
  // правая стенка
  P[imax + 1][j] = P[imax][j];
}
for (i = 1; i <= imax; i++)
{
  P[i][0] = P[i][1];
  P[i][jmax + 1] = P[i][jmax];
}

Граничные условия на препятствиях

Препятствия представлены флагом C_B. Граничные условия для них ставятся по такому же принципу как и для внешних стенок.Приведу 2 примера простановки давления:

if (IsObstacle(i, j))
{
   // если снизу от препятствия - вода - то копируем значение P из нее
          if (IsFluid(i, j - 1))
          {
            P[i][j] = P[i][j - 1];
          }
   // если слева - вода ...
          else if (IsFluid(i - 1, j))
          {
            P[i][j] = P[i - 1][j];
          }
  // .......
}

Для угловой клетки берем среднее по значениям окружающих ее водных клеток.Например возмём препятствие, слева и сверху от него будет вода.Тогда давление в клетке-препятствии считаем так:

if (IsFluid(i - 1, j) && IsFluid(i, j + 1))
{
  P[i][j] = (P[i][j + 1] + P[i - 1][j]) / 2;
}

Граничные условия на поверхности

Поверхность и ее движение моделируется с помощью частиц. (Исходники с граничными условиями на поверхности, сделанные как описано в данном разделе — находятся в папке simpletestobstacle.)

Изначально частицы помещаются в клетки с жидкостью по 4 штуки на клетку (по 1 возле каждого угла). Далее частицы на каждом шаге перемещаются используя простой метод Эйлера из классической механики. Скорости для движения берутся в каждой клетке как средние по всей клетке(хотя не проблема использовать например интерполяцию).

  x = particles[k].x;
  y = particles[k].y;
// определяем координаты клетки в которой находятся частицы
  i = (int)(x / delx);
  j = (int)(y / dely);
  u = U[i][j];
  v = V[i][j];
  // собственно сам метод Эйлера для движения частиц
  x += delt * u;
  y += delt * v;

На каждом шаге клетки с частицами помечаются как вода.Остальные — это пустые клетки, в них расчет основных переменных (u,v,p) не производится.

Для расчетов основных переменных, необходимо задать граничные условия на поверхности и соседними с ней клетками, также как это требовалось для стенок. Но сначала нужно определить какие клетки, из помеченных как вода — принадлежат к поверхности, а также с какой стороны находится воздух. Для этих целей используется 2 массива — FLAG и FLAGSURF. В первом задаются только типы клеток — вода, воздух (пусто) и препятствия. Вот соответствующие флаги (сокращения B — boundary F — fluid E — empty):

public const int C_B = 0x0000; //препятствие
public const int C_F = 0x0010;//вода
public const int C_E = 0x1000;//пусто

Массив FLAGSURF используется для определения поверхностных клеток, для остальных клеток значение там =0. Флаги в этом массиве определяют не только тип клетки, но и все комбинации соседних клеток, в которых пусто. Флаги сделаны как стандартные битовые маски, чтобы их можно было комбинировать.
Каждое значение в FLAGSURF содержит 4 бита которые соответствуют 4 сторонам (соседним клеткам).
Если бит установлен в 1 то в соответствующей соседней клетке — пусто. Если 0 — то там вода.
Расположение битов: 0000 NSWO 0000 0000 — буквами обозначены 4 стороны N (North север) S (South юг) W (West восток) и O (запад).

Весь список флагов есть в исходниках, поэтому приведу лишь некоторые примеры значений:

public const int C_W = 0x0200;// 512
в двоичном виде значение выглядит так 0000 0010 0000 0000
Здесь флаг соответствующий стороне W установлен в 1. Это значит что слева от текущей клетки — пусто.
В тоже время остальные 3 бита установлены в 0 — значит остальные соседние клетки наполнены водой.

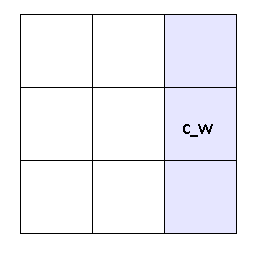
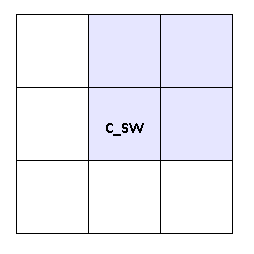
public const int C_SW = 0x0600;// 1536 0000 0110 0000 0000
Здесь флаг соответствующий сторонам W и S установлен в 1. Значит слева и снизу от текущей клетки — пусто, а остальные клетки — водные

При определении типов поверхностных клеток и заполнении массива FLAGSURF соответствующие биты устанавливаются в 1 таким образом:

// если слева пусто, то установим соответствующий бит  в 1
if (FLAG[i-1][j] == GG.C_E)
  FLAGSURF[i][j] = FLAGSURF[i][j] | GG.C_W;

Массив FLAGSURF в основном нужен только для удобства простановки граничных условий на поверхности. Поскольку для разных типов поверхностных клеток применяются разные граничные условия. Как уже говорилось, нам необходимо проставить граничные условия в пустых клетках, которые находятся рядом с поверхностными клетками и также граничные условия нужны в самих поверхностных клетках, поскольку у нас staggered сетка и в расчет переменных u v входят не все поверхностные клетки.

Принцип простановки значений простой. Т.к. давление воздуха в 1000 раз меньше давления в воде — то им можно пренебречь и дать возможность воде свободно перемещаться вдоль поверхности, никак не ограничивая ее скорости и не изменяя направления движения. Конечно в моей схеме не учитывается поверхностное натяжение, иначе все было бы гораздо сложней.

Мы проставляем значения скоростей U и V в поверхностных клетках и граничащих с ними пустых клетках не забывая при этом то, что у нас staggered сетка.
Значения для простановки берутся из соседних водных клеток.Осталось только решить из каких именно соседних клеток все это берется, потому что таких клеток может быть несколько.

Вот скрин с граничными условиями которые нужно проставить.Синие квадраты — вода. Черные метки — требующиеся граничные условия. Обратите внимание что метки расположены частично в поверхностных клетках а частично в пустых. Так получается, потому что в коде решателя у нас есть такие условия (как видно — в клетках перед правой граничной стенкой расчет U V не производится):

        if (IsFluid(i, j) && IsFluid(i+1, j)){
          F[i][j] = ...
        }

Рассмотрим несколько примеров:

клетка с флагом C_SW

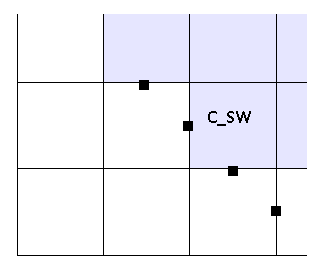
          case GG.C_SW:
            {
              U[i][j - 1] = U[i][j];
              V[i][j - 1] = V[i][j];
              U[i - 1][j] = U[i][j];
              V[i - 1][j] = V[i][j];
            } break;

Здесь значения в самой клетки нам не нужны — они будут рассчитаны в решателе. Но зато нужны значения в соседних пустых клетках — т.к. в решателе есть термы с U[i][j — 1] и т.д.

Ближайшая водная клетка к этим пустым клеткам — это клетка [i][j] из нее и берутся значения U и V.
Из рисунка видно, что значение для V[i — 1][j] можно было бы взять как из клетки [i][j], так и из [i — 1][j+1] — но в общем случае клетка [i — 1][j+1] может оказаться не водной к тому же значение V в ней может тоже оказаться грани��ным и еще не будет проставлено.Поэтому правильный вариант — [i][j] т.к значения в ней будут рассчитаны в решателе.

клетка с флагом C_W

          case GG.C_W:
            {
              U[i - 1][j] = U[i][j];
              V[i - 1][j] = V[i][j];
            } break;

Здесь все аналогично.

клетка с флагом C_NW

          case GG.C_NW:
            {
              V[i][j] = V[i][j - 1];
              U[i - 1][j] = U[i][j];
            } break;

Здесь значение U в самой клетке будет рассчитано в решателе, т.к. справа от нее есть водная клетка. А вот V нужно проставить, поскольку клетка сверху — пустая.Также необходимо задать значение U[i — 1][j], тк при расчете U[i][j] потребуются значения и в соседних с ней клетках, в том числе и в U[i — 1][j].

Точно также, как и в предыдущем случае значение V[i][j] берем из клетки V[i][j — 1], а не из V[i-1][j] — тк значение в V[i-1][j] может оказаться граничным и еще не известным.

Давление в пустых клетках и клетках поверхности ставим = 0. Это не совсем корректно, но это работает.
В поверхностных клетках давление нужно, потому что при решении уравнения для давления эти клетки являются граничными и в них расчет давления непосредственно не производится.

Алгоритм движения жидкости с помощью частиц только на поверхности

В исходниках присутствуют варианты с именем track в названии. Это метод перемещения свободной поверхности, в котором перемещаются частицы только на самой поверхности, а не во всем объеме жидкости. Это в некоторой степени похоже на метод VOF — но там делается предварительная реконструкция поверхности, что достаточно громоздко. В моем методе если частица ушла из клетки то она помечается пустой, а в находящиеся рядом клетки жидкости в которых нет частиц — добавляются частицы, чтобы знать где находится поверхность. Если же частица переходить в пустую клетку — то клетка помечается как жидкость. Конечно у данного метода есть приличная доля неточности, но зато он быстрый и не требует сложного кодирования.

Implicit схема расчета

В исходниках есть также implicit версия решателя — применяется к уравнениям для скоростей, отличия в коде от explicit версии там минимальные. При дискретизации просто все термы с U и V[i][j] переходят в левую часть уравнения а не в правую как в explicit.Implicit (неявная) схема позволяет делать значительно большие шаги по времени, что в случае с explicit невозможно.
Про implicit можно почитать тут http://math.mit.edu/cse/codes/mit18086_navierstokes.pdf.

3D версия

В 3D версии сделано все по аналогии с 2D.
Управление клавишами F1-F8 + WASD, стрелки и E R PgUp PgDown для поворота камеры.
Для сцен с источником воды — клавиша P — для включения отключения напора воды.
G — получше рендеринг поверхности (вместо кубов используются сферы), но жутко тормозит.
В папке Demos — находятся сцены и параметры (размеры, шаг по времени, гравитация и кол-во частиц на клетку) в виде xml файла. Также есть возможность нарисовать в paint свой HeightMap (карту высот), размеры могут быть любые — есть autoresize.

В заключение приведу скрины из 2D и 3D:

Остальные скрины тут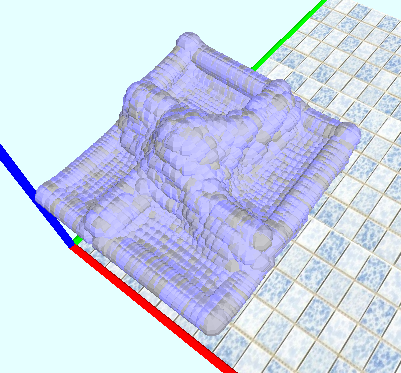

Исходники лежат тут sourceforge.

Проекты которые есть в исходниках

Все написано на Visual Studio 2010
— Adaptive Mesh Refinement — клетки разбиваются на более мелкие части и в этих дочерних ячейках тоже считаются
все переменные, при этом крупные клетки являются соседними к дочерним при дискритизации
fluid2subcell*
— implicit версия
fluide2dimplicit\ и fluide2dimplicitfree\
— программа разбита на модули, которые легко заменять на другие версии, не удаляя старые
fluide2dmodule\
— движение воды реализовано через движение частиц только на поверхности
fluide2dtrack*
— рабочая версия с explicit методом и граничными условиями на поверхности, которые описаны в данном посте
simpletestobstacle\
— вместо безразмерного Re — используются реальные коэффициенты плотности воды и вязкости ,
что позволяет при решении уравнений сразу получать настоящие скорости и реальное давление в массивах U V P
simpletestobstaclereal\
— все что есть в папке finite volume относится к этому методу
сделано по книге:
Introduction to computational fluid dynamics The finite volume method Versteeg HK Malalasek

— теперь 3D
— простейший вариант — без поверхности и препятствий
SimpleFluid3D\
— самый последний вариант со всем всем всем на с++
fluid3dunion\
— вариант для GPU ( только вода ), написан на OpenCL, на моей GeForce 550 ускорение в 7 раз (без каких либо оптимизаций специально под gpu)
fluid3clsimple\
— очень ранняя версия того что есть в fluid3dunion — версия рабочая, но есть много недоработок, на c#, explicit
fluide3tao

Ссылки по теме

Хорошая статья есть тут Kalland_Master.pdf
и тут Кратко о гидродинамике: уравнения движения

Книги:
— Griebel M Dornseifer T Numerical simulation in fluid dynamics SIAM 1998
// эту книгу особенно отмечу, с нее фактически все началось у меня, исходники к ней легко можно найти, лучшего описания реализации cfd я до сих пор не нашел)

— Bridson R. Fluid Simulation for Computer Graphics
— Anderson JDJr Computational fluid dynamics The basics with applications MGH 1995
— Charles Hirsch-Numerical Computation of Internal and External Flows 2007
— Gretar Tryggvason Direct Numerical Simulations of Gas-Liquid Multiphase Flows
— Versteeg HK Malalasek Introduction to computational fluid dynamics The finite volume method

Все книги можно найти сами знаете где.

P.S. Если есть люди, знакомые с CFD, было бы интересно вместе улучшить данный проект в плане скорости и корректности решения (особенно при моделировании поверхности).
Рендеринг я и сам смогу запилить более — менее, а вот математика и физика — это не основное мое направление. Буду рад любым замечаниям и полезным советам.