Однажды для нашего проекта потребовался функционал прокладки маршрутов. Программистов у нас не то чтобы очень много, а скорее наоборот, поэтому мы хотели найти какое-то готовое решение, поискали и ничего хорошего не нашли.
Данные дорожного графа у нас были, но в таком виде, что ни в одну библиотеку или какой-то middle-ware их так просто не подать. Да и middle-ware по навигации, честно говоря, мы не нашли, так чтобы просто встраивалось в нашу систему (спасибо, если кто подскажет куда посмотреть). Поэтому приняли решение сделать самостоятельно, используя по максимуму существующие библиотеки для всего.
О процессе разработки сервиса и расскажу.
О графе.
Несколько слов о данных. Данные мы получаем от стороннего поставщика, на формат и состав данных влиять не можем. Данные о дорогах имеют вид файла в формате ArcView (Shapefile). Все улицы разбиты на сегменты от перекрестка до перекрестка, каждому сегменту сопоставлены атрибуты:
— уникальный идентификатор сегмента
— геометрическая ломаная, изображающая сегмент дороги
— данные о разрешенной максимальной скорости по ПДД
— данные о возможности разворота в начале и конце сегмента
— признак одностороннего движения на сегменте
— Z уровень начала и конца сегмента (например въезд на эстакаду имеет в начале уровень 0, а в конце уровень 1)
Кроме того есть отдельный файл с ограничениями движения, накладываемыми логикой и/или ПДД. Каждое ограничение — это вектор идентификаторов, ссылающихся на сегменты улицы (из первого файла), последовательное движение по которым запрещено.
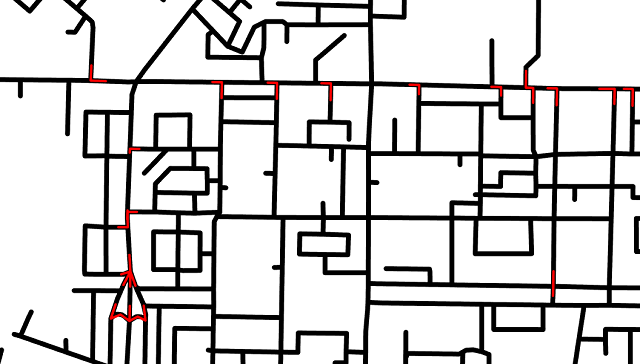
Пример того, как все это выглядит, висит в заголовке поста (красным — запреты, к сожалению, наш софт в данном случае не позволяет нарисовать запреты с направлением).
Для работы алгоритмов на графе, требуется, чтобы граф был представлен в каком-то общепринятом виде, например в виде списка связанности вершин, или матрицы связанности. То есть фактически требуются данные о вершинах и связях между ними. Поскольку в наших данных сведения о вершинах очень неполные, есть только данные об их геометрическом местоположении, пришлось провести обработку, чтобы все вершины получили уникальные идентификаторы.
За основу мы взяли геометрическое местоположение вершин, но было одно обстоятельство: координаты конечных вершин сегментов не всегда совпадали на 100%, например на перекрестках (возможно дефекты работы операторов ГИС системы, точно не знаю). Поэтому мы приняли решение считать одной вершиной графа все конечные точки сегментов, имеющие одинаковый Z-уровень и отстоящие друг от друга не дальше чем на 1 метр.
Всего сегментов уличной дорожной сети в наших данных примерно 140 000, а значит конечных точек примерно 280 000. Соответственно нужен был какой-то нелобовой алгоритм нахождения всех соседей на расстоянии до 1 метра каждой точки. Лобовой перебор всех пар имеет квадратичную сложность и работает чрезмерно долго. Поскольку мы решили, что наша программка будет работать напрямую с исходным представлением данных, то есть с Shape-файлами (причины: легко обновлять, не нужно поддерживать, документировать, версионировать собственный формат хранения), то нужен был эффективный алгоритм идентификации вершин.
Придумали вот что (здесь и далее код на С++):
1. Сделали контейнер для ребер графа:
Мультимэп, потому что мы решили не вводить новые идентификаторы сегментов/ребер графа, а информацию о прямом и обратном ребре сохранять соответственно с одинаковыми идентификаторами. Вероятно это было не самое правильное решение, потому что на мой взгляд усложнило логику некоторых процедур, но в начале казалось, что так будет нормально.
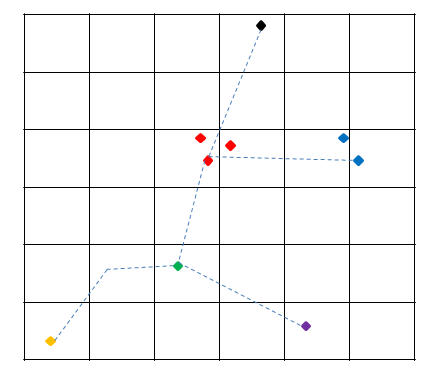
Рис 1.
2. Координатную плоскость разбили на квадратики метр на метр (рис 1).
Каждой вершине сопоставили ключ:
3. Сделали хэш-контейнер
При просмотре списка сегментов уличной сети, мы строим список элементов, содержащих идентификаторы начальной и конечной вершин, идентификатор ребра, и сопутствующую информацию, то есть фактически граф в виде списка смежных вершин.
Начальную и конечную точку сегмента мы пробуем добавить в SPHash по вычисленному в п. 2 ключу. Если с таким ключом в контейнере уже есть точки, то новую точку не добавляем, а возвращаем идентификатор уже имеющейся (при условии что имеющаяся точка в контейнере на том же Z уровне что и добавляемая).
Если по ключу в контейнере ничего нет, то вносим точку в контейнер и возвращаем идентификатор добавленной точки.
Правда точки, расстояние между которыми меньше 1 метра, могут иметь разные ключи, поэтому мы проверяем контейнер не только по вычисленному ключу, но и по 8-ми соседним:
merge() строит список идентификаторов ближайших точек в векторе near.
Получив список идентификаторов соседей (по сути кандидатов на слияние в одну вершину), мы сравниваем точки, вычисляя точное евклидово расстояние между ними. И если оно меньше заданного, то считаем, что точки одинаковы и объединяем в одну вершину (на рисунке покрашены в один цвет), возвращая идентификатор подходящей вершины уже имеющейся в ячейке с ключом getKey(xPart, yPart).
При старте эта обработка занимает около 1 секунды, что нас устроило.
4. В результате получаем, что соседние точки ближе заданного порога получают один идентификатор.
Теперь у нас есть список смежных вершин. Временная сложность получения такого списка линейно зависит от количества вершин, потому что каждую мы обрабатываем ровно 1 раз, а операции поиска и вставки в хэш-контейнер имеет асимптотически константную сложность.
Как вы уже, должно быть, заметили, мы не обрабатываем промежуточные вершины ломаной уличного сегмента, так как на топологию графа они не влияют (в середине сегмента нельзя осуществить никакого маневра, во всяком случае у нас нет об этом данных).
Если бы мы разбили ломаную на составляющие ее отрезки и каждый отрезок считали бы ребром, то в графе вместо примерно 140 000 ребер было бы уже примерно 600 000. Значительно возросло бы время поиска пути, в конце я покажу эту разницу в абсолютных значениях.
Остался последний штрих. Ограничения, или запрещенные маневры.
Ограничение запрещает какой-либо маневр, например поворот налево на перекрестке. Исходно в данных представляет собой список сегментов, последовательное движение по которым запрещено.
Приведу пример:
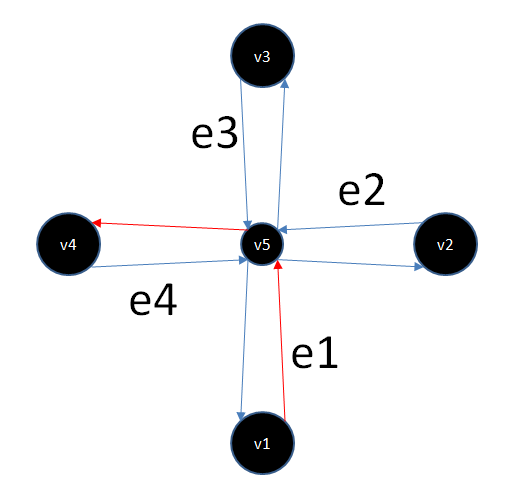
Рис. 2
Красные стрелки показывают запрещенный маневр, числа обозначают идентификаторы сегментов. Фактически в данных этот запрет выглядит как {e1, e4}.
С таким представлением запретов работать в процессе прокладки маршрута очень тяжело, поэтому мы решили локально трансформировать граф так, чтобы запрещенный маневр был невозможен в графе чисто топологически, при этом все прочие разрешенные маневры остались возможными.
Для этого мы продублировали вершины, входящие в запрещенные маневр. И через эти дублированные вершины провесили ребра так, чтобы создать разрешенные маневры, а для запрещенного маневра такой маршрут просто не создавать.
При клонировании вершины ее геометрическое местоположение остается прежним (показанные на рисунке вершины v6 и v5 на самом деле геометрически в одном и том же месте и разнесены на рисунке для удобства), для новой вершины, разумеется, выделяется новый идентификатор.
Проиллюстрирую сказанное на примере перекрестка с запрещенным левым поворотом выше:
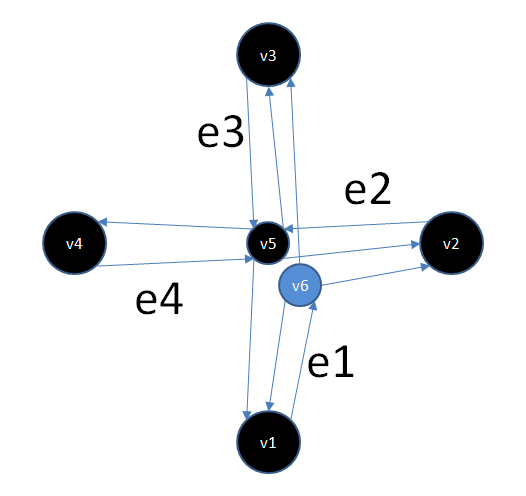
Рис 3.
Видно, что на графе с измененной топологией осуществить левый поворот по запрещенному пути на перекрестке больше нельзя, при этом все разрешенные маневры остались возможными.
Ограничения из более чем 2-х ребер обрабатываются по тому же принципу, но порождают больше новых вершин и ребер, на размер графа эти трансформации влияют, но не значительно (рост числа ребер примерно на 5%). В наших данных порядка 5000 ограничений из двух сегментов и около 400 из трех).
Вот иллюстрация того, как трансформируется граф под действием ограничения из 3-х ребер:
Было:
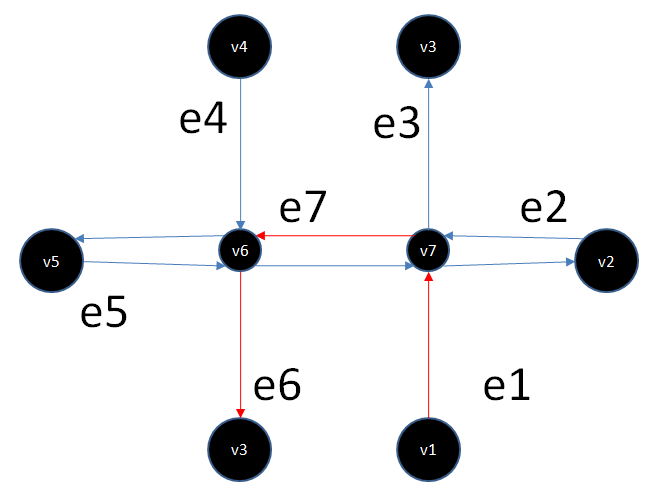
Рис 4.
Стало:
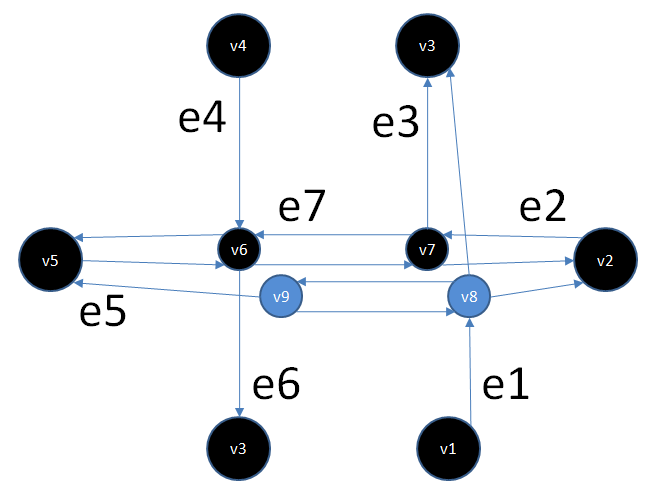
Рис 5.
Надо сказать, что реализация алгоритма трансформации графа стала самым сложным этапом всей работы (на нее ушло около 30% времени) и именно там было наибольшее число багов. Отчасти это связано с не самой хорошей проработкой структуры хранения данных. Так что если что-то осталось непонятным — не страшно, это действительно было непросто, задавайте вопросы, постараюсь ответить.
Об инструментах.
И так теперь у нас был граф представленный в удобном виде с учетом всех ограничений, по которому можно было прокладывать маршруты. В качестве алгоритма решили попробовать классический алгоритм Дейкстры, хорошая реализация которого есть в библиотеке boost.
Тут добавить особо нечего, по boost::graph есть хорошая документация и даже книги, мы взяли код одного из примеров и с небольшими изменениями использовали его у нас.
Следующим этапом стала обработка запросов. Мы решили, что удобно, если сервис сможет прокладывать маршрут, имея только начальную и конечную точку, заданные координатами. А значит надо быстро найти начальную и конечную вершину в графе, которые максимально близко расположены к соответствующим точкам запроса.
Для этого нужно было быстро уметь находить ближайшую к заданной пользователем точку на уличной сети (пользователь может захотеть маршрут от точки находящейся вне дорожно-уличной сети).
Тут уместно вспомнить о том, что сегменты дорожно-уличной сети в наших данных это ломаные, поэтому нам надо было найти ближайшую к заданной точку на ломаной (это может быть точка лежащая на ломаной, либо ее начальная или конечная вершина).
Ломаных довольно много (140 000), а искать надо быстро. Искать перебором всех сегментов слишком медленно. Тут на помощь пришла свежая версия библиотеки boost::geometry, где появились пространственные индексы (boost::geometry::index) уже с поддержкой такого объекта как ломаная линия (linestring).
С использованием этого индекса мы быстро находим несколько ближайших кандидатов, из них затем точным алгоритмом определяется сегмент, наиболее близко проходящий возле заданной точки.
Для чтения SHP файлов мы использовали библиотеку GDAL, для преобразования между географическими системами координат (мы работаем в локальной системе города, так исторически сложилось), а пользователю удобнее использовать GPS (WGS84) координаты) взяли библиотеку proj4, а для задач преобразования кодировки текста iconv.
О деталях.
— маршрут к середине ребра
Напомню что наш граф — топологическое представление дорожной сети, геометрические детали для работы алгоритма Дейкстры неважны. Но геометрический аспект важен для пользователя. Вспомним, что алгоритм Дейкстры строит кратчайшие маршруты от заданной вершины графа до всех остальных (включая искомую конечную вершину).
Значит начальную вершину мы должны определить, но поиск по индексу мы ведем среди ломаных, то есть фактически среди ребер. Как понять от какой вершины (в графе) нужно прокладывать маршрут, ведь промежуточных вершин сегмента там нет, а значит надо выбрать либо начальную, либо конечную вершину найденного сегмента.
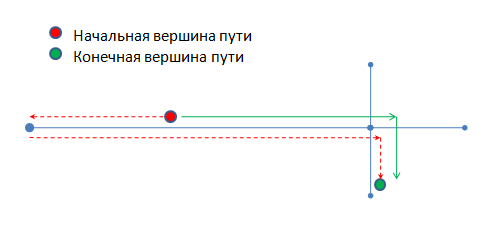
Рис 6.
Однако для пользователя такое решение не будет удобным, представьте длиннющее шоссе, без поворотов и разворотов (а такое случается нередко). Пользователю будет очень удивительно видеть как маршрут построился от точки, находящейся в километре от той, что он задал (потому что на ближайшем сегменте других вершин ближе не оказалось). Это плохо. Кроме того, как показано на рисунке 6 (красные пунктирные линии) выбор ближайшей вершины сегмента иногда будет означать более длинный путь до цели, что вовсе нехорошо. Значит нам надо было как-то создать видимость того, что вершин в нашем графе больше и расположены они чаще, но так, чтобы это не повлияло на время работы алгоритма поиска пути.
Были рассмотрены несколько подходов со своими достоинствами и недостатками:
1) два поиска и от начальной и от конечной вершин сегмента и выбор того пути, который короче с учетом расстояния от точки пользователя с соответствующего конца сегмента.
плюс: просто в реализации
минус: двойной поиск кратчайшего пути с соответствующим замедлением времени работы.
2) создание избыточного графа: все геометрические вершины сегментов дорожной сети превращаются в вершины графа.
плюс: просто в реализации
минусы: значительный рост времени работы алгоритма Дейкстры, в ряде случае не решает проблемы (прямой длинный участок дороги)
3) дополнение графа временными вершинами и ребрами в момент запроса и возврат графа в начальное состояние после того, как найден маршрут.
плюс: один поиск маршрута, не нужно раздувать граф, быстро работает.
минус: сложнее в реализации чем остальные методы
Мы выбрали третий путь. В граф временно добавляется вершина, соответствующая ближайшей к пользовательской точке, лежащей на ломаной сегмента и 2 ребра (соответствующие частям сегмента до начальной и конечной вершин, либо только какой-то один из них, если сегмент с односторонним движением) эти вершина и ребра добавляются в граф, производится поиск, после чего временные вершина и ребра удаляются из графа.
— вывод в веб
На самом деле наша программа вообще не работает с сетью, она читает стандартный ввод и пишет ответ в стандартный вывод, а весь интерфейс с сетью и диспетчеризация сделаны отдельной программкой на node.js.
— многопоточность
Тут все просто. Наша программа работает в 1 поток. Но если очень нужно загрузить все ядра сервера, то можно запустить по 1 экземпляру на каждое ядро, благо 1 процесс требует для хранения графа, порядка 300 Мб (и этот размер можно сократить раза в 2-3, но мы себе пока такую задачу не ставили за ненадобностью). Как распределять запросы по процессам? Поскольку у нас есть внешняя программа диспетчер, она может заняться распределением запросов к работающим процессам, а также мониторить их работоспособность и т.д.
Другой вариант загрузки всех ядер: создание многопоточной программы на С++, нам показался сложнее. Во-первых надо было бы писать сетевой код на С++ (на node.js у нас написана практически вся серверная часть проекта и мы знали, что сделать работу с сетью на нем намного проще), либо делать более сложный интерфейс к внешнему диспетчеру по сравнению с stdin/stdout. Во-вторых у нас не read-only граф из-за временных вершин и ребер, а значит нужно было бы очень осторожно синхронизировать рабочие потоки, чтобы с одной стороны не убить производительность, а с другой не налететь на соответствующие проблемы многопоточного кода, мы не нашли преимуществ у этого подхода (на данный момент), чтобы так делать.
В заключении небольшая статистика:
Вся программа получилась всего 1500 строк, плюс несколько десятков строк диспетчера на node.js, кодированием на С++ занимался 1 человек, времени ушло около 1 месяца + помогали с идеями и отладкой еще пара коллег. Как нам кажется довольно неплохо для такой не самой элементарной задачи.
Среднее время поиска маршрута (на Core i7 3.4 Ghz) около 60-65 мс. Кстати я обещал сказать время работы на графе, где каждый отрезок ломаной дорожного сегмента превращается в отдельное ребро графа, это около 250 мс, заметная разница, согласитесь.
Спасибо за внимание тем, кто дочитал до конца.
Данные дорожного графа у нас были, но в таком виде, что ни в одну библиотеку или какой-то middle-ware их так просто не подать. Да и middle-ware по навигации, честно говоря, мы не нашли, так чтобы просто встраивалось в нашу систему (спасибо, если кто подскажет куда посмотреть). Поэтому приняли решение сделать самостоятельно, используя по максимуму существующие библиотеки для всего.

О процессе разработки сервиса и расскажу.
О графе.
Несколько слов о данных. Данные мы получаем от стороннего поставщика, на формат и состав данных влиять не можем. Данные о дорогах имеют вид файла в формате ArcView (Shapefile). Все улицы разбиты на сегменты от перекрестка до перекрестка, каждому сегменту сопоставлены атрибуты:
— уникальный идентификатор сегмента
— геометрическая ломаная, изображающая сегмент дороги
— данные о разрешенной максимальной скорости по ПДД
— данные о возможности разворота в начале и конце сегмента
— признак одностороннего движения на сегменте
— Z уровень начала и конца сегмента (например въезд на эстакаду имеет в начале уровень 0, а в конце уровень 1)
Кроме того есть отдельный файл с ограничениями движения, накладываемыми логикой и/или ПДД. Каждое ограничение — это вектор идентификаторов, ссылающихся на сегменты улицы (из первого файла), последовательное движение по которым запрещено.
Пример того, как все это выглядит, висит в заголовке поста (красным — запреты, к сожалению, наш софт в данном случае не позволяет нарисовать запреты с направлением).
Для работы алгоритмов на графе, требуется, чтобы граф был представлен в каком-то общепринятом виде, например в виде списка связанности вершин, или матрицы связанности. То есть фактически требуются данные о вершинах и связях между ними. Поскольку в наших данных сведения о вершинах очень неполные, есть только данные об их геометрическом местоположении, пришлось провести обработку, чтобы все вершины получили уникальные идентификаторы.
За основу мы взяли геометрическое местоположение вершин, но было одно обстоятельство: координаты конечных вершин сегментов не всегда совпадали на 100%, например на перекрестках (возможно дефекты работы операторов ГИС системы, точно не знаю). Поэтому мы приняли решение считать одной вершиной графа все конечные точки сегментов, имеющие одинаковый Z-уровень и отстоящие друг от друга не дальше чем на 1 метр.
Всего сегментов уличной дорожной сети в наших данных примерно 140 000, а значит конечных точек примерно 280 000. Соответственно нужен был какой-то нелобовой алгоритм нахождения всех соседей на расстоянии до 1 метра каждой точки. Лобовой перебор всех пар имеет квадратичную сложность и работает чрезмерно долго. Поскольку мы решили, что наша программка будет работать напрямую с исходным представлением данных, то есть с Shape-файлами (причины: легко обновлять, не нужно поддерживать, документировать, версионировать собственный формат хранения), то нужен был эффективный алгоритм идентификации вершин.
Придумали вот что (здесь и далее код на С++):
1. Сделали контейнер для ребер графа:
typedef size_t EdgeID; typedef size_t VertexID; struct EdgeDesc { VertexID vtxSrc, vtxDest; EdgeInfo info; }; typedef std::unordered_multimap<EdgeID, EdgeDesc> EdgeMap;
Мультимэп, потому что мы решили не вводить новые идентификаторы сегментов/ребер графа, а информацию о прямом и обратном ребре сохранять соответственно с одинаковыми идентификаторами. Вероятно это было не самое правильное решение, потому что на мой взгляд усложнило логику некоторых процедур, но в начале казалось, что так будет нормально.

Рис 1.
2. Координатную плоскость разбили на квадратики метр на метр (рис 1).
Каждой вершине сопоставили ключ:
static_assert(sizeof(size_t) >= 8, "size_t type should be 64 bit or larger"); auto keyPartX = [this](double x) { return (size_t)(x - bound_.first.x) + 1; }; auto keyPartY = [this](double y) { return (size_t)(y - bound_.first.y) + 1; }; auto getKey = [](size_t x, size_t y) { return x << (sizeof(size_t) / 2 * 8) | y; }; auto getKeyXY = [&keyPartX, &keyPartY, &getKey](double x, double y) { return getKey(keyPartX(x), keyPartY(y)); };
3. Сделали хэш-контейнер
typedef size_t CellKey; typedef std::unordered_map<CellKey, std::vector<VertexID>> SPHash;
При просмотре списка сегментов уличной сети, мы строим список элементов, содержащих идентификаторы начальной и конечной вершин, идентификатор ребра, и сопутствующую информацию, то есть фактически граф в виде списка смежных вершин.
Начальную и конечную точку сегмента мы пробуем добавить в SPHash по вычисленному в п. 2 ключу. Если с таким ключом в контейнере уже есть точки, то новую точку не добавляем, а возвращаем идентификатор уже имеющейся (при условии что имеющаяся точка в контейнере на том же Z уровне что и добавляемая).
Если по ключу в контейнере ничего нет, то вносим точку в контейнер и возвращаем идентификатор добавленной точки.
Правда точки, расстояние между которыми меньше 1 метра, могут иметь разные ключи, поэтому мы проверяем контейнер не только по вычисленному ключу, но и по 8-ми соседним:
std::vector<size_t> near; size_t xPart = keyPartX(p.x); size_t yPart = keyPartY(p.y); near.clear(); merge(near, getKey(xPart, yPart)); merge(near, getKey(xPart + 1, yPart)); merge(near, getKey(xPart - 1, yPart)); merge(near, getKey(xPart, yPart + 1)); merge(near, getKey(xPart, yPart - 1)); merge(near, getKey(xPart + 1, yPart + 1)); merge(near, getKey(xPart + 1, yPart - 1)); merge(near, getKey(xPart - 1, yPart + 1)); merge(near, getKey(xPart - 1, yPart - 1));
merge() строит список идентификаторов ближайших точек в векторе near.
Получив список идентификаторов соседей (по сути кандидатов на слияние в одну вершину), мы сравниваем точки, вычисляя точное евклидово расстояние между ними. И если оно меньше заданного, то считаем, что точки одинаковы и объединяем в одну вершину (на рисунке покрашены в один цвет), возвращая идентификатор подходящей вершины уже имеющейся в ячейке с ключом getKey(xPart, yPart).
При старте эта обработка занимает около 1 секунды, что нас устроило.
4. В результате получаем, что соседние точки ближе заданного порога получают один идентификатор.
Теперь у нас есть список смежных вершин. Временная сложность получения такого списка линейно зависит от количества вершин, потому что каждую мы обрабатываем ровно 1 раз, а операции поиска и вставки в хэш-контейнер имеет асимптотически константную сложность.
Как вы уже, должно быть, заметили, мы не обрабатываем промежуточные вершины ломаной уличного сегмента, так как на топологию графа они не влияют (в середине сегмента нельзя осуществить никакого маневра, во всяком случае у нас нет об этом данных).
Если бы мы разбили ломаную на составляющие ее отрезки и каждый отрезок считали бы ребром, то в графе вместо примерно 140 000 ребер было бы уже примерно 600 000. Значительно возросло бы время поиска пути, в конце я покажу эту разницу в абсолютных значениях.
Остался последний штрих. Ограничения, или запрещенные маневры.
Ограничение запрещает какой-либо маневр, например поворот налево на перекрестке. Исходно в данных представляет собой список сегментов, последовательное движение по которым запрещено.
Приведу пример:

Рис. 2
Красные стрелки показывают запрещенный маневр, числа обозначают идентификаторы сегментов. Фактически в данных этот запрет выглядит как {e1, e4}.
С таким представлением запретов работать в процессе прокладки маршрута очень тяжело, поэтому мы решили локально трансформировать граф так, чтобы запрещенный маневр был невозможен в графе чисто топологически, при этом все прочие разрешенные маневры остались возможными.
Для этого мы продублировали вершины, входящие в запрещенные маневр. И через эти дублированные вершины провесили ребра так, чтобы создать разрешенные маневры, а для запрещенного маневра такой маршрут просто не создавать.
При клонировании вершины ее геометрическое местоположение остается прежним (показанные на рисунке вершины v6 и v5 на самом деле геометрически в одном и том же месте и разнесены на рисунке для удобства), для новой вершины, разумеется, выделяется новый идентификатор.
Проиллюстрирую сказанное на примере перекрестка с запрещенным левым поворотом выше:

Рис 3.
Видно, что на графе с измененной топологией осуществить левый поворот по запрещенному пути на перекрестке больше нельзя, при этом все разрешенные маневры остались возможными.
Ограничения из более чем 2-х ребер обрабатываются по тому же принципу, но порождают больше новых вершин и ребер, на размер графа эти трансформации влияют, но не значительно (рост числа ребер примерно на 5%). В наших данных порядка 5000 ограничений из двух сегментов и около 400 из трех).
Вот иллюстрация того, как трансформируется граф под действием ограничения из 3-х ребер:
Было:

Рис 4.
Стало:

Рис 5.
Надо сказать, что реализация алгоритма трансформации графа стала самым сложным этапом всей работы (на нее ушло около 30% времени) и именно там было наибольшее число багов. Отчасти это связано с не самой хорошей проработкой структуры хранения данных. Так что если что-то осталось непонятным — не страшно, это действительно было непросто, задавайте вопросы, постараюсь ответить.
Об инструментах.
И так теперь у нас был граф представленный в удобном виде с учетом всех ограничений, по которому можно было прокладывать маршруты. В качестве алгоритма решили попробовать классический алгоритм Дейкстры, хорошая реализация которого есть в библиотеке boost.
Тут добавить особо нечего, по boost::graph есть хорошая документация и даже книги, мы взяли код одного из примеров и с небольшими изменениями использовали его у нас.
Следующим этапом стала обработка запросов. Мы решили, что удобно, если сервис сможет прокладывать маршрут, имея только начальную и конечную точку, заданные координатами. А значит надо быстро найти начальную и конечную вершину в графе, которые максимально близко расположены к соответствующим точкам запроса.
Для этого нужно было быстро уметь находить ближайшую к заданной пользователем точку на уличной сети (пользователь может захотеть маршрут от точки находящейся вне дорожно-уличной сети).
Тут уместно вспомнить о том, что сегменты дорожно-уличной сети в наших данных это ломаные, поэтому нам надо было найти ближайшую к заданной точку на ломаной (это может быть точка лежащая на ломаной, либо ее начальная или конечная вершина).
Ломаных довольно много (140 000), а искать надо быстро. Искать перебором всех сегментов слишком медленно. Тут на помощь пришла свежая версия библиотеки boost::geometry, где появились пространственные индексы (boost::geometry::index) уже с поддержкой такого объекта как ломаная линия (linestring).
С использованием этого индекса мы быстро находим несколько ближайших кандидатов, из них затем точным алгоритмом определяется сегмент, наиболее близко проходящий возле заданной точки.
Для чтения SHP файлов мы использовали библиотеку GDAL, для преобразования между географическими системами координат (мы работаем в локальной системе города, так исторически сложилось), а пользователю удобнее использовать GPS (WGS84) координаты) взяли библиотеку proj4, а для задач преобразования кодировки текста iconv.
О деталях.
— маршрут к середине ребра
Напомню что наш граф — топологическое представление дорожной сети, геометрические детали для работы алгоритма Дейкстры неважны. Но геометрический аспект важен для пользователя. Вспомним, что алгоритм Дейкстры строит кратчайшие маршруты от заданной вершины графа до всех остальных (включая искомую конечную вершину).
Значит начальную вершину мы должны определить, но поиск по индексу мы ведем среди ломаных, то есть фактически среди ребер. Как понять от какой вершины (в графе) нужно прокладывать маршрут, ведь промежуточных вершин сегмента там нет, а значит надо выбрать либо начальную, либо конечную вершину найденного сегмента.

Рис 6.
Однако для пользователя такое решение не будет удобным, представьте длиннющее шоссе, без поворотов и разворотов (а такое случается нередко). Пользователю будет очень удивительно видеть как маршрут построился от точки, находящейся в километре от той, что он задал (потому что на ближайшем сегменте других вершин ближе не оказалось). Это плохо. Кроме того, как показано на рисунке 6 (красные пунктирные линии) выбор ближайшей вершины сегмента иногда будет означать более длинный путь до цели, что вовсе нехорошо. Значит нам надо было как-то создать видимость того, что вершин в нашем графе больше и расположены они чаще, но так, чтобы это не повлияло на время работы алгоритма поиска пути.
Были рассмотрены несколько подходов со своими достоинствами и недостатками:
1) два поиска и от начальной и от конечной вершин сегмента и выбор того пути, который короче с учетом расстояния от точки пользователя с соответствующего конца сегмента.
плюс: просто в реализации
минус: двойной поиск кратчайшего пути с соответствующим замедлением времени работы.
2) создание избыточного графа: все геометрические вершины сегментов дорожной сети превращаются в вершины графа.
плюс: просто в реализации
минусы: значительный рост времени работы алгоритма Дейкстры, в ряде случае не решает проблемы (прямой длинный участок дороги)
3) дополнение графа временными вершинами и ребрами в момент запроса и возврат графа в начальное состояние после того, как найден маршрут.
плюс: один поиск маршрута, не нужно раздувать граф, быстро работает.
минус: сложнее в реализации чем остальные методы
Мы выбрали третий путь. В граф временно добавляется вершина, соответствующая ближайшей к пользовательской точке, лежащей на ломаной сегмента и 2 ребра (соответствующие частям сегмента до начальной и конечной вершин, либо только какой-то один из них, если сегмент с односторонним движением) эти вершина и ребра добавляются в граф, производится поиск, после чего временные вершина и ребра удаляются из графа.
— вывод в веб
На самом деле наша программа вообще не работает с сетью, она читает стандартный ввод и пишет ответ в стандартный вывод, а весь интерфейс с сетью и диспетчеризация сделаны отдельной программкой на node.js.
— многопоточность
Тут все просто. Наша программа работает в 1 поток. Но если очень нужно загрузить все ядра сервера, то можно запустить по 1 экземпляру на каждое ядро, благо 1 процесс требует для хранения графа, порядка 300 Мб (и этот размер можно сократить раза в 2-3, но мы себе пока такую задачу не ставили за ненадобностью). Как распределять запросы по процессам? Поскольку у нас есть внешняя программа диспетчер, она может заняться распределением запросов к работающим процессам, а также мониторить их работоспособность и т.д.
Другой вариант загрузки всех ядер: создание многопоточной программы на С++, нам показался сложнее. Во-первых надо было бы писать сетевой код на С++ (на node.js у нас написана практически вся серверная часть проекта и мы знали, что сделать работу с сетью на нем намного проще), либо делать более сложный интерфейс к внешнему диспетчеру по сравнению с stdin/stdout. Во-вторых у нас не read-only граф из-за временных вершин и ребер, а значит нужно было бы очень осторожно синхронизировать рабочие потоки, чтобы с одной стороны не убить производительность, а с другой не налететь на соответствующие проблемы многопоточного кода, мы не нашли преимуществ у этого подхода (на данный момент), чтобы так делать.
В заключении небольшая статистика:
Вся программа получилась всего 1500 строк, плюс несколько десятков строк диспетчера на node.js, кодированием на С++ занимался 1 человек, времени ушло около 1 месяца + помогали с идеями и отладкой еще пара коллег. Как нам кажется довольно неплохо для такой не самой элементарной задачи.
Среднее время поиска маршрута (на Core i7 3.4 Ghz) около 60-65 мс. Кстати я обещал сказать время работы на графе, где каждый отрезок ломаной дорожного сегмента превращается в отдельное ребро графа, это около 250 мс, заметная разница, согласитесь.
Спасибо за внимание тем, кто дочитал до конца.