
«В 1997 году Deep Blue обыграл в шахматы Каспарова.
В 2011 Watson обставил чемпионов Jeopardy.
Сможет ли ваш алгоритм в 2013 году отличить Бобика от Пушистика?»
Эта картинка и предисловие — из челленджа на Kaggle, который проходил осенью прошлого года. Забегая вперед, на последний вопрос вполне можно ответить «да» — десятка лидеров справилась с заданием на 98.8%, что на удивление впечатляет.
И все-таки — откуда вообще берется такая постановка вопроса? Почему задачи на классификацию, которые легко решает четырехлетний ребенок, долгое время были (и до сих пор остаются) не по зубам программам? Почему распознавать предметы окружающего мира сложнее, чем играть в шахматы? Что такое deep learning и почему в публикациях о нем с пугающим постоянством фигурируют котики? Давайте поговорим об этом.
Что вообще значит «распознать»?
Предположим, что у нас есть две категории и много-много картинок, которые нужно разложить в две соответствующие категориям стопки. По какому принципу мы будем это делать? Замечательный ответ на этот вопрос состоит в том, что никто точно не знает, но общепринятый подход такой: мы будем искать в картинках какие-то «интересные» нам куски данных, которые будут встречаться только у одной из категорий. Такие куски данных называются features, а сам подход — feature detection. Существуют достаточно уверенные доводы в пользу того, что как-то так работает и биологический мозг — первым делом, конечно, знаменитый эксперимент Хьюбела и Визеля на клетках кошачьей (опять) зрительной коры.
О терминах
В отечественной литературе про машинному обучению вместо feature пишут «признак», что, по-моему, звучит как-то размыто. Здесь я буду говорить «фича», да простится мне это издевательство над русским языком.
Мы никогда не знаем заранее, какие части нашей картинки могут использоваться как хорошие фичи. В их роли может выступать все, что угодно — фрагменты изображения, форма, размер или цвет. Фича запросто может даже не присутствовать на картинке сама, а выражаться в параметре, полученным каким-то образом из исходных данных — например, после использования фильтра границ. Ок, давайте посмотрим на пару примеров с нарастающей сложностью:

Допустим, мы хотим сделать гугл-кар, который мог бы отличать правые повороты от левых и соответствующим образом поворачивать руль. Правило для обнаружения хорошей фичи можно придумать почти на пальцах: отрезаем верхнюю половину картинки, выделяем участок определенного оттенка (асфальт), прикладываем к нему слева какую-нибудь логарифмическую кривую. Если весь асфальт поместился под кривой — то у нас поворот направо, иначе — налево. Можно набрать себе несколько кривых на случай поворотов разной кривизны — и, конечно, разный набор оттенков асфальта, включающий в себя сухое и мокрое состояние. Правда, на грунтовых дорогах наша фича окажется бесполезной.
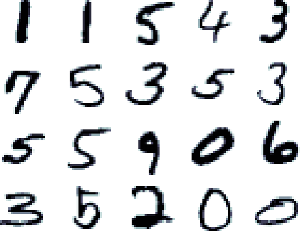
Пример из датасета рукописных цифр MNIST — эту картинку, наверное, видел каждый, кто хоть немного знаком с машинным обучением. У каждой цифры есть характерные геометрические элементы, которые определяют, что это за цифра — завиток внизу у двойки, косая черта через все поле у единицы, два состыкованных круга у восьмерки и т.д. Мы можем составить себе набор фильтров, которые будут выделять эти существенные элементы, потом поочередно прикладывать эти фильтры к нашему изображению, и кто покажет лучший результат — тот, скорее всего, и есть правильный ответ.
Фильтры эти будут выглядеть, например, вот так
Картинка из курса Джоффри Хинтона «Neural networks for machine learning»
Кстати, обратите внимание на цифры 7 и 9 — у них отсутствует нижняя часть. Дело в том, что у семерки и девятки она одинаковая, и полезной информации для распознания не несет — поэтому нейросеть, которая вырабатывала эти фичи, проигнорировала этот элемент. Обычно для получения таких фич-фильтров мы как раз и пользуемся обычными однослойными нейронными сетями или чем-то похожим.

Картинка из курса Джоффри Хинтона «Neural networks for machine learning»
Кстати, обратите внимание на цифры 7 и 9 — у них отсутствует нижняя часть. Дело в том, что у семерки и девятки она одинаковая, и полезной информации для распознания не несет — поэтому нейросеть, которая вырабатывала эти фичи, проигнорировала этот элемент. Обычно для получения таких фич-фильтров мы как раз и пользуемся обычными однослойными нейронными сетями или чем-то похожим.
Ок, ближе к теме. Как насчет такого?

Различий между этими двумя картинками очень много — глаза разбегаются. Уровень яркости, цвета, или вот например забавное совпадение — у левой картинки белый цвет преобладает в левой части, а у правой — в правой. Но нам нужно выбрать не любые, а именно те, которые однозначно будут определять кошек или собак. То есть, например, следующие две картинки должны распознаться как принадлежащие одной категории:

Если долго и внимательно смотреть на них и пытаться понять, что между ними общего, то в голову приходит разве что форма ушей — они более-менее одинаковые, только справа наклонены. Но это тоже совпадение — можно легко себе представить (и найти примеры из того же набора данных) фотографию, на которой кот смотрит не в ту сторону, наклоняет голову или вообще запечатлен сзади. Остальное — все разное. Масштаб, цвет и длина шерсти, глаз, поза, фон… Вообще ничего общего — и тем не менее, небольшое устройство в вашей голове способно с высочайшей точностью и безошибочно отнести эти две картинки к одной категории, а две те, что повыше — к разным. Не знаю, как вас, а меня иногда восхищает, что такой могущественный девайс находится совсем рядом у каждого из нас, только руку протянуть — и тем не менее, мы до сих пор не можем понять, как он работает.
Пятиминутка оптимизма (и теории)
Ладно. А все-таки, если попробовать задать наивный вопрос — чем кошки визуально отличаются от собак? Мы можем с легкостью начать список — размер, пушистость, усы, форма лап, наличие характерных поз, которые они могут принимать… Или, например, у кошек нет бровей. Проблема в том, что все эти отличительные признаки выражены не на языке пикселей. Мы не можем заложить их в алгоритм, пока предварительно не объяснили ему, что такое эти самые брови и где они должны находиться — или что такое лапы и откуда они растут. Более того, мы, в общем-то, делаем все эти алгоритмы распознавания для того, чтобы понимать, что перед нами кошка — существо, к которому применимы понятия «усы», «лапы» и «хвост» — а до этого мы даже не можем с достаточной уверенностью сказать, где на фотографии заканчиваются обои или диван, и начинается кошка. Круг замкнулся.
Но некоторый вывод отсюда сделать все-таки можно. Когда мы формулировали фичи в предыдущих примерах, мы исходили из возможной изменчивости объекта. Поворот дороги может быть только влево или вправо — других вариантов нет (кроме проезда прямо, конечно, но там и делать ничего не надо), плюс стандарты дорожного строительства гарантируют нам, что поворот будет достаточно плавным, а не под прямым углом. Поэтому мы конструируем свою фичу так, чтобы она допускала различную кривизну поворота, определенный набор оттенков дорожного покрытия, и на этом возможная изменчивость заканчивается. Следующий пример: цифра «1» может быть написана разным почерком, и все варианты будут отличаться друг от друга — но в ней обязательно должна присутствовать прямая вертикальная (или наклонная) черта, иначе она перестанет быть единицей. Когда мы подготавливаем свою фичу-фильтр, мы оставляем классификатору пространство для изменчивости — и если взглянуть на картинку под спойлером снова, можно увидеть, что активная часть фильтра для единицы представляет собой толстую полосу, которая позволяет нарисовать черту с разным наклоном и с допустимым острым углом в верхней части.
В случае с котами «пространство для маневра» наших объектов становится неизмеримо огромным. На картинке могут быть коты разных пород, большие и маленькие, на любом фоне, какой только можно придумать, их может частично загораживать какой-нибудь объект, и конечно, они могут принимать сто тысяч различных поз — и это мы еще не упоминали про трансляцию (перенос объекта на картинке в сторону), вращение и масштабирование — вечную головную боль всех классификаторов. Составить плоский фильтр, аналогичный предыдущему, который мог бы учитывать все эти изменения, кажется невозможной задачей — попробуем мысленно совместить тысячи разных форм на одной картинке, и мы получим бесформенное пятно фильтра, которое будет положительно реагировать на все подряд. Значит, искомые фичи должны должны представлять собой какую-то более сложную структуру. Какую — пока непонятно, но она должна иметь возможность учитывать в себе все эти возможные изменения.
Это «пока непонятно» длилось довольно долго — большую часть истории машинного обучения. Но вдруг в какой-то момент люди поняли об окружающем мире одну увлекательную идею. Звучит она примерно так:
Все вещи состоят из других, маленьких и более элементарных вещей.
Когда я говорю «все вещи», я имею в виду буквально все, что угодно, чему мы способны обучаться. В первую очередь, раз этот пост про зрение — конечно, объекты окружающего мира, изображенные на картинках. Любой видимый объект, продолжаем мы мысль, можно представить в виде композиции каких-то устойчивых элементов, а те, в свою очередь состоят из геометрических фигур, а те — сочетание линий и углов, расположенных в определенном порядке. Примерно вот так:

(почему-то не нашел хорошей информативной картинки, поэтому эта вырезана из выступления Эндрю Ына (основатель Coursera) про deep learning
Кстати, в рамках наивных размышлений можно сказать, что наша речь и естественный язык (которые тоже давно считаются вопросами искусственного интеллекта) представляет собой структурную иерархию, где буквы складываются в слова, слова — в словосочетания, а те, в свою очередь, в предложения и текст — и что при встрече с новым словом нам не приходится заново учить все буквы, входящие в него, а незнакомые тексты мы вообще не воспринимаем как нечто требующее специального запоминания и обучения. Если заглянуть в историю, можно обнаружить множество подходов, которые в той или иной степени (и в основном, гораздо более научно обоснованно) высказывали эту мысль:
1. Уже упоминавшиеся Хьюбел и Визель в своем эксперименте в 1959 году обнаружили в зрительной коре мозга клетки, реагирующие на определенные символы на экране — и кроме этого обнаружили существование других клеток «уровнем выше», которые, в свою очередь, реагируют на определенные устойчивые сочетания сигналов от клеток первого уровня. На основании этого они предположили существование целой иерархии аналогичных клеток-детекторов.
прекрасный отрывок видео из эксперимента
… где демонстрируется, как они почти случайно обнаружили нужную фичу, которая заставляла нейрон реагировать — сдвинув чуть дальше обычного образец так, что край стекла попал в камеру. Чувствительным людям смотреть осторожно, в наличии издевательства над животными.
2. Где-то в районе двухтысячных в среде специалистов машинного обучения появляется сам термин deep learning — применительно к нейронным сетям, у которых не один слой нейронов, а много — и которые, таким образом, могут обучаться нескольким уровням фич. Подобная архитектура имеет вполне строго обоснованные преимущества — чем больше уровней в сети, тем более сложные функции она может выражать. Немедленно возникает проблема с тем, как обучать такие сети — повсеместно использовавшийся раньше алгоритм обратного распространения ошибки (backpropagation) плохо работает с большим количеством слоев. Появляется несколько разных моделей для этих целей — автоэнкодеры, ограниченные машины Больцмана и т.д.
3. Джефф Хокинс в своей книге «Об интеллекте» в 2004 году пишет, что иерархический подход рулит и за ним будущее. Он уже слегка опоздал к началу бала, но не могу о нем не упомянуть — в книге эта мысль выводится из совершенно повседневных вещей и простым языком, человеком, который был достаточно далек от машинного обучения и вообще говорил, что все эти ваши нейронные сети — плохая идея. Почитайте книгу, она очень вдохновляет.
Немного о кодах
Итак, у нас есть гипотеза. Вместо того, чтобы запихивать в обучающий алгоритм 1024x768 равноправных пикселей и смотреть, как он медленно задыхается от нехватки памяти и неспособности понять, какие пиксели важны для распознавания, мы хотим извлечь из картинки некоторую иерархическую структуру, которая будет состоять из разных уровней. На первом уровне мы предполагаем увидеть какие-то самые базовые, структурно простые элементы картинки — ее строительные кирпичи: границы, штрихи, отрезки. Повыше — устойчивые комбинации фич первого уровня (например, углы), еще выше — фичи, скомпонованные из предыдущих (геометрические фигуры, и т.д.). Собственно, вопрос — откуда взять такую структуру для отдельной картинки?
Давайте в качестве отвлеченного вопроса немного поговорим о кодах.
Когда мы хотим представить объект из реального мира в компьютере, мы пользуемся каким-то набором правил, чтобы перевести этот объект, по кусочкам, в цифровой вид. Букве, например, ставится в сопоставление байт (в ASCII), а картинка разбивается на много маленьких пикселей, и каждый из них выражается набором чисел, которые передают яркость и цветовую информацию. Моделей представления цвета много, и хотя, вообще говоря, не все равно, какую использовать для обучения — для простоты пока представим себе черно-белый мир, где один пиксель представляется числом от 0 до 1, выражающим его яркость — от черного до белого.
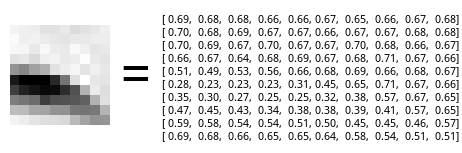
Что не так с этим представлением? Каждый пиксель здесь — независим, передает только небольшую часть информации о итоговой картинке. Это, с одной стороны, приятно и выгодно, когда нам нужно куда-то сохранить картинку или передать по сети, потому что она занимает меньше места, с другой — неудобно для распознавания. В нашем случае мы видим здесь наклонный штрих (немного с изгибом) в нижней части изображения — отсюда сложно догадаться, но это деталь контура носа с фотографии лица. Так вот, в данном случае нам важны те пиксели, которые составляют этот штрих, важна граница между черным и белым — а едва уловимая игра света в оттенках светло-серого в верхней части квадратика совершенно не важна, и не стоит даже тратить на нее вычислительные ресурсы. Но в этом представлении нам приходится иметь дело со всеми пикселями сразу — каждый из них ничем не лучше другого.
Давайте теперь представим себе другой код. Разложим этот квадратик на линейную сумму других таких же квадратиков, каждый из которых умножен на коэффициент. Можно себе представить, как мы берем много пластин темного стекла с разной прозрачностью, и на каждой пластине нарисованы различные штрихи — вертикальные, горизонтальные, разные. Мы кладем эти пластины стопкой друг на друга, и настраиваем прозрачность так, чтобы получить нечто похожее на наш рисунок — не идеальное, но достаточное для целей распознавания.
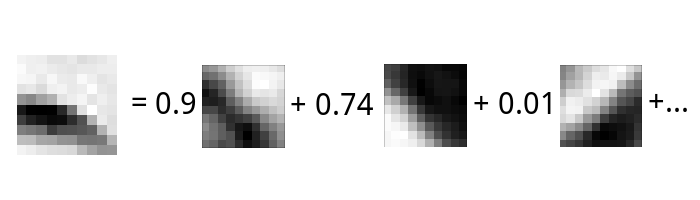
Наш новый код состоит из функциональных элементов — каждый из них теперь говорит что-то о присутствии в исходном квадратике какого-то отдельного осмысленного компонента. Видим коэффициент 0.01 у компонента с вертикальным штрихом — и понимаем, что в образце мало «вертикальности» (зато много «косого штриха» — см. первый коэффициент). Если мы независимым образом выберем компоненты этого нового кода, его словарь, то можно ожидать, что ненулевых коэффициентов будет немного — такой код называется разреженным (sparse).
Полезные свойства такого представления можно увидеть на примере одного из приложений под названием denoising autoencoder. Если взять изображение, разбить его на небольшие квадраты размером, допустим, 10x10, и для каждого кусочка подобрать соответствующий код — то мы можем с впечатляющей эффективностью затем очищать это изображение от случайного шума и искажений, переводя зашумленное изображение в код и восстанавливая обратно (пример можно найти, например, здесь). Это показывает, что код нечувствителен к случайному шуму, и сохраняет те части изображения, которые нужны нам для восприятия объекта — благодаря чему мы считаем, что шума после восстановления стало «меньше».
Обратной стороной такого подхода оказывается то, что новый код тяжеловесней — в зависимости от количества компонентов, бывший квадратик 10x10 пикселей может утяжелиться в значительно большей степени. Чтобы оценить масштаб — есть свидетельства того, что зрительная кора головного мозга человека кодирует 14x14 пикселей (размерность 196) с помощью примерно 100000 нейронов.
А еще мы внезапно получили первый уровень иерархии — он как раз и состоит из элементов словаря этого кода, которые, как сейчас можно будет убедиться, представляют собой штрихи и границы. Осталось откуда-то взять этот самый словарь.
Пятиминутка практики
Воспользуемся пакетом scikit-learn — библиотекой для машинного обучения к SciPy (Python). И конкретно, классом (сюрприз) MiniBatchDictionaryLearning. MiniBatch — потому что алгоритм будет не над всем датасетом сразу, а поочередно над небольшими, случайно выбранными пачками данных. Процесс прост и занимает десять строчек кода:
from sklearn.decomposition import MiniBatchDictionaryLearning
from sklearn.feature_extraction.image import extract_patches_2d
from sklearn import preprocessing
from scipy.misc import lena
lena = lena() / 256.0 # тестовое изображение
data = extract_patches_2d(lena, (10, 10), max_patches=1000) # извлекаем тысячу кусочков 10x10 - обучающую выборку
data = preprocessing.scale(data.reshape(data.shape[0], -1)) # rescaling - сдвигаем значения симметрично нуля, и чтобы стандартное отклонение равнялось 1
learning = MiniBatchDictionaryLearning(n_components=49)
features = learning.fit(data).components_
Если нарисовать то, что лежит в features, получится примерно следующее:
Вывод через pylab
import pylab as pl
for i, feature in enumerate(features):
pl.subplot(7, 7, i + 1)
pl.imshow(feature.reshape(10, 10),
cmap=pl.cm.gray_r, interpolation='nearest')
pl.xticks(())
pl.yticks(())
pl.show()

Тут можно ненадолго остановиться и вспомнить, зачем мы все это изначально делали. Мы хотели получить набор достаточно независимых друг от друга «строительных кирпичиков», из которых складывается изображенный объект. Чтобы этого добиться, мы нарезали много-много маленьких квадратных кусочков, прогнали их через алгоритм, и получили, что все эти квадратные кусочки можно с достаточной степенью достоверности для распознавания представить в виде композиции вот таких компонентов. Поскольку на уровне 10x10 пикселей (хотя, конечно, зависит от разрешения картинки) мы сталкиваемся только с краями и границами, то их же и получаем в результате, все — с необходимостью разные.
Это закодированное представление мы можем использовать в качестве детектора. Чтобы понять, является ли случайно выбранный кусок картинки краем или границей, мы берем его и просим scikit подобрать эквивалентный код, вот так:
patch = lena[0:10, 0:10]
code = learning.transform(patch)
Если какой-нибудь один из компонентов кода имеет достаточно большой коэффициент по сравнению с остальными — то мы знаем, что это сигнализирует от присутствии соответствующего вертикального, горизонтального или еще какого-нибудь штриха. Если все компоненты примерно одинаковы — значит, в этом месте на картинке однотонный фон или шум, который интереса для нас не представляет.
Но мы хотим двигаться дальше. Для этого понадобится еще несколько преобразований.
Итак, любой фрагмент размера 10x10 теперь можно выразить последовательностью из 49 чисел, каждое из которых будет означать коэффициент прозрачности для соответствующего компонента на картинке выше. А теперь возьмем эти 49 чисел и запишем в форме квадратной матрицы 7x7 — и нарисуем то, что получилось.
А получилось следующее (два примера для наглядности):
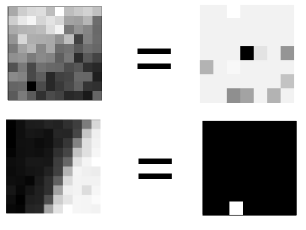
Слева — фрагмент оригинального изображения. Справа — его кодированное представление, где каждый пиксель — уровень присутствия в коде соответствующего компонента (чем светлее, тем сильнее). Можно заметить, что на первом фрагменте (верхнем) нет четко выраженного штриха, и его код выглядит смешением всего подряд в слабой бледно-серой интенсивности, а на втором четко присутствует один компонент — а остальные все равны нулю.
Теперь, чтобы обучить второй уровень иерархии, возьмем из оригинальной картинки фрагмент побольше (так, чтобы в него помещалось несколько маленьких — скажем, 30x30), разрежем его на маленькие фрагменты и представим каждый из них в кодированом варианте. Потом состыкуем обратно вместе, и на таких данных обучим еще один DictionaryLearning. Логика простая — если наша первоначальная идея правильна, то находящиеся рядом края и границы должны тоже складываться в устойчивые и повторяющиеся сочетания.

То, что получилось в результате на примере, не выглядит чем-то осмысленным на первый взгляд, но это только на взгляд. Вот, например, что получается во втором уровне иерархии, которую тренировали на человеческих лицах.
многовато картинок как-то
Тут, правда, размер фрагмента выбран побольше — 25x25 вместо 10x10. Одна из неприятных особенностей этого подхода — необходимость самому настраивать размер «минимальной смысловой единицы».

Тут, правда, размер фрагмента выбран побольше — 25x25 вместо 10x10. Одна из неприятных особенностей этого подхода — необходимость самому настраивать размер «минимальной смысловой единицы».
Некоторые трудности возникают с тем, чтобы нарисовать полученный «словарь», потому что второй уровень обучается на коде первого, и компоненты его будут выглядеть как пестрое крошево точек с рисунка выше. Для этого нам нужно сделать еще один шаг вниз — снова разбить эти компоненты на части, и «раскодировать» их при помощи первого уровня, но здесь этот процесс детально рассматривать не будем.
А дальше уровни наращиваются до тех пор, пока это необходимо, по совершенно такому же принципу. Вот, например, третий. И тут мы уже видим что-то интересное:

Каждое лицо здесь — фича размером 160x160. В нашем распоряжении несколько наиболее встречающихся расположений — фронтальное, пол-оборота направо и налево, плюс разные цвета кожи. При этом каждая фича имеет под собой еще два слоя, которые, во-первых, позволяют быстро проверять тестовые изображения на валидность, а во-вторых, дают дополнительное количество свободы — контуры и границы могут отклоняться от идеальных линий, но пока они остаются в рамках фич своего уровня, у них есть возможность просигнализировать о своем присутствии наверх.
Not bad.
И что — все, мы победили?
Очевидно, нет. На самом деле, если запустить тот же скрипт, которым я рисую все эти наборы, на искомом датасете про кошек и собак, картина будет крайне удручающая — уровень за уровнем нам будет возвращаться примерно одни и те же фичи, изображающие слегка изогнутые границы.
ок, это точно последняя
Одну собачью морду получилось заловить, но это чистая случайность — потому что похожий силуэт встретился в выборке, допустим, два раза. Если запустить скрипт еще раз, она может не появиться.

Одну собачью морду получилось заловить, но это чистая случайность — потому что похожий силуэт встретился в выборке, допустим, два раза. Если запустить скрипт еще раз, она может не появиться.
Наш подход страдает из-за того же, за что мы раскритиковали обычные feed-forward нейронные сети. DictionaryLearning в процессе обучения пытается искать некоторые общие места, структурные компоненты выбранных фрагментов картинки. В случае с лицами у нас все получилось, потому что они более-менее похожи друг на друга — вытянутые овальные формы с некоторым количеством отклонений (а несколько уровней иерархии дает нам больше свободы в этом отношении). В случае с котиками — уже не получается, потому что во всем датасете с трудом можно отыскать два похожих силуэта. Алгоритм не находит ничего общего между картинками в тестовой выборке — исключая первые уровни, где мы все еще имеем дело со штрихами и границами. Фэйл. Опять тупик.
Идеи на будущее
На самом деле, если подумать — выборка с большим количеством разных котиков хороша в том плане что охватывает разнообразие пород, поз, размеров и окрасок, но возможно, не слишком удачна для обучения даже нашего с вами интеллекта. В конце концов, мы учимся скорее методом многократных повторений и наблюдения за объектом, а не быстрым проглядыванием всех возможных его вариаций. Чтобы научиться играть на фортепиано, нам приходится постоянно играть гаммы — а было бы неплохо, если бы для этого достаточно было бы прослушать тысячу классических произведений. Итак, идея номер раз — уйти от разнообразия в выборке и сконцентрироваться на одном объекте в одной и той же сцене, но, скажем, в разных позициях.
Идея номер два вытекает из первой, и озвучивалась уже многими, в том числе упомянутым Джеффом Хокинсом — попытаться извлечь пользу из времени. В конце концов, разнообразие форм и поз, которое мы наблюдаем у одного объекта, мы видим во времени — и можем, для начала, группировать последовательно поступающие картинки, считая, что на них изображен один и тот же кот, просто каждый раз в несколько новой позе. А это значит, что нам, как минимум, придется кардинально сменить обучающую выборку, и вооружиться роликами с ютуба, найденными по запросу «kitty wakes up». Но об этом — в следующей серии.
Посмотреть на код
… можно на гитхабе. Запуск через python train.py myimage.jpg (можно также указать папку с картинками), плюс дополнительные параметры настройки — количество уровней, размер фрагментов и т.д. Требует scipy, scikit-learn и matplotlib.
Полезные ссылки и что еще можно вводного почитать про deep learning
- A Primer on Deep Learning — информативный пост с историей вопроса, кратким введением и гораздо более красивыми картинками.
- UFLDL Tutorial — туториал от уже упоминавшегося Andrew Ng из Стэнфорда — to get your hands dirty. Здесь буквально все, чтобы познакомиться с тем, как это работает — введение, математика процесса, параллели с feed-forward сетями, иллюстрированые примеры и упражнения в Matlab/Octave.
- Бесплатная онлайновая книга Neural Networks and Deep Learning — к сожалению, еще не закончена. В достаточно популярном виде описывает основы, начиная с перцептронов, моделей нейронов и т.д.
- Джоффри Хинтон рассказывает про новые поколений нейронных сетей
- Последний talk с Хокинсом, где он вкратце излагает примерно то же, что в своей книге, но больше конкретики. О том, что должен уметь интеллектуальный алгоритм, что известные свойства человеческого мозга говорят нам про это, чем нас не устраивают нейронные сети, и чем полезен sparse coding.