Фрактальное броуновское движение (ФБД) относится к классу рассматриваемых функций, заданные на конечном интервале и равные нулю вне его, которые включают кусочно непрерывные функции, удовлетворяющие условию роста:
 ,
,
где функция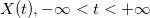 , удовлетворяет условию:
, удовлетворяет условию: 
Преобразование Фурье
Для ФБД будем интерпретировать процесс как временной процесс. Существует частотная область, в которой функция — сумма составляющих, имеющих определенную частоту. Функция
как временной процесс. Существует частотная область, в которой функция — сумма составляющих, имеющих определенную частоту. Функция  может быть разложена как
может быть разложена как 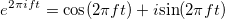 .
.
Составляющая с частотой
с частотой  имеет вид:
имеет вид:
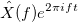 , где
, где 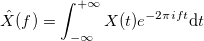 .
.
Функция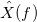 называется преобразованием Фурье.
называется преобразованием Фурье.
Спектральная плотность
Полная энергия исходного процесса равна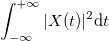 .
.
По теореме Планшереля: .
.
Средняя мощность функции на отрезке
на отрезке 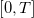 определяется как
определяется как 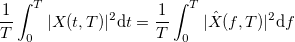 .
.
Тогда спектральная плотность мощности равна:
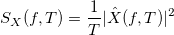
Если длина отрезка стремиться к бесконечности, то:
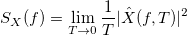 .
.
Т.к. функция описывает ФБД с параметром Хёрста, то:
описывает ФБД с параметром Хёрста, то:

Дискретное преобразование Фурье ФБД
Процесс моделирования ФБД можно упростить через аппроксимацию преобразования Фурье с помощью рядов Фурье с учетом сохранения свойств спектральной плотности. После этого, использовав обратное преобразование Фурье, получим ФБД.
Если

то функция вещественнозначная.
вещественнозначная.
Таким образом, приведенный ниже алгоритм использует это условие сопряженной симметрии.
Алгоритм построения кривой ФБД:
 — нормально-распределенная случайная величина с нулевым мат ожиданием и единичным стандартным отклонением.
— нормально-распределенная случайная величина с нулевым мат ожиданием и единичным стандартным отклонением.
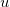 — равномерно-распределенная случайная величина на единичном отрезке.
— равномерно-распределенная случайная величина на единичном отрезке.

На рисунке изображены некоторые вариации ФБД для различных показателей Хёрста.
Пример использования генерации ФБД
Дан исходных ряд валютной пары доллар-рубль за период: 05.05.2005 — 01.05.2015.
Рассчитаем доходности обменного курса и с помощью RS-анализа найдем показатель Хёрста для пары доллар-рубль: H=0.64 отстоит от среднего значения E(H)=0.52 на 5.64 стандартных отклонений. Величина H – значима. Ряд персистентный, т.к. H>0.5, нормированный размах изменяет масштаб быстрее, чем квадратный корень по времени, процесс имеет долгосрочную память (подробнее в [1]).
Отсутствие цикла позволяет, используя параметр Хёрста, смоделировать фрактальный шум с помощью фильтрации Фурье. Построим в частотной области преобразование Фурье фрактального броуновского движения со случайными амплитудами и фазами, удовлетворяющие свойству спектральной плотности. C помощью обратного преобразования Фурье получим требуемый фрактальный шум.
Далее генерируем 10000 всевозможных вариаций ФБД с показателем Хёрста 0.64. Таким образом получаем распределение прогнозных значений для валютного курса.

На рисунке изображен график исходного ряда значений курсов доллар-рубль, и 90%-дециль распределения и математическое ожидание прогноза: с вероятностью 90% можно утверждать, что курс не превысит значений верхней кривой, среднее значение обменного курса имеет нисходящий тренд, в середине мая в среднем цена за доллар составит 52.3 рубля, начало июня – 51.6, начало июля – цена опуститься до отметки в 48.7 рублей.
Список литературы:
 ,
,где функция
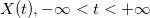 , удовлетворяет условию:
, удовлетворяет условию: 
Преобразование Фурье
Для ФБД будем интерпретировать процесс
 как временной процесс. Существует частотная область, в которой функция — сумма составляющих, имеющих определенную частоту. Функция
как временной процесс. Существует частотная область, в которой функция — сумма составляющих, имеющих определенную частоту. Функция  может быть разложена как
может быть разложена как 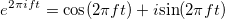 .
.Составляющая
 с частотой
с частотой  имеет вид:
имеет вид: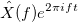 , где
, где 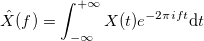 .
.Функция
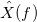 называется преобразованием Фурье.
называется преобразованием Фурье.Спектральная плотность
Полная энергия исходного процесса равна
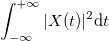 .
.По теореме Планшереля:
 .
.Средняя мощность функции
 на отрезке
на отрезке 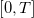 определяется как
определяется как 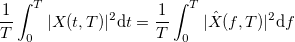 .
.Тогда спектральная плотность мощности равна:
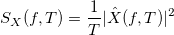
Если длина отрезка стремиться к бесконечности, то:
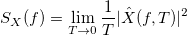 .
.Т.к. функция
 описывает ФБД с параметром Хёрста, то:
описывает ФБД с параметром Хёрста, то:
Дискретное преобразование Фурье ФБД
Процесс моделирования ФБД можно упростить через аппроксимацию преобразования Фурье с помощью рядов Фурье с учетом сохранения свойств спектральной плотности. После этого, использовав обратное преобразование Фурье, получим ФБД.
Если

то функция
 вещественнозначная.
вещественнозначная.Таким образом, приведенный ниже алгоритм использует это условие сопряженной симметрии.
Алгоритм построения кривой ФБД:
 — нормально-распределенная случайная величина с нулевым мат ожиданием и единичным стандартным отклонением.
— нормально-распределенная случайная величина с нулевым мат ожиданием и единичным стандартным отклонением.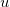 — равномерно-распределенная случайная величина на единичном отрезке.
— равномерно-распределенная случайная величина на единичном отрезке.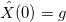
- Для
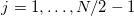 значения преобразования Фурье
значения преобразования Фурье 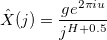
- Для
 —
— 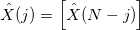
- Для каждого
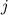 рассчитываем: амплитуду (абсолютная величина комплексного числа
рассчитываем: амплитуду (абсолютная величина комплексного числа 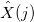 ), фазу (значение аргумента комплексного числа
), фазу (значение аргумента комплексного числа 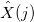 , т.е. угол, выраженный в радианах)
, т.е. угол, выраженный в радианах) - Рассчитываем значения ФБД:
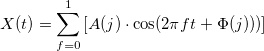

На рисунке изображены некоторые вариации ФБД для различных показателей Хёрста.
Пример использования генерации ФБД
Дан исходных ряд валютной пары доллар-рубль за период: 05.05.2005 — 01.05.2015.
Рассчитаем доходности обменного курса и с помощью RS-анализа найдем показатель Хёрста для пары доллар-рубль: H=0.64 отстоит от среднего значения E(H)=0.52 на 5.64 стандартных отклонений. Величина H – значима. Ряд персистентный, т.к. H>0.5, нормированный размах изменяет масштаб быстрее, чем квадратный корень по времени, процесс имеет долгосрочную память (подробнее в [1]).
Отсутствие цикла позволяет, используя параметр Хёрста, смоделировать фрактальный шум с помощью фильтрации Фурье. Построим в частотной области преобразование Фурье фрактального броуновского движения со случайными амплитудами и фазами, удовлетворяющие свойству спектральной плотности. C помощью обратного преобразования Фурье получим требуемый фрактальный шум.
Далее генерируем 10000 всевозможных вариаций ФБД с показателем Хёрста 0.64. Таким образом получаем распределение прогнозных значений для валютного курса.

На рисунке изображен график исходного ряда значений курсов доллар-рубль, и 90%-дециль распределения и математическое ожидание прогноза: с вероятностью 90% можно утверждать, что курс не превысит значений верхней кривой, среднее значение обменного курса имеет нисходящий тренд, в середине мая в среднем цена за доллар составит 52.3 рубля, начало июня – 51.6, начало июля – цена опуститься до отметки в 48.7 рублей.
Список литературы:
- Гончаренко А.В. Фрактальный анализ динамики валютной пары USD/RUB // Риск-менеджмент в кредитной организации. №2(18). 2015. С. 18-22.