актуальная редакция статьи на сайте Makeloft
Думаю, что для многих людей аудиокомпрессия с потерями напоминает магический чёрный ящик, где удивительно сложным образом с применением математической алхимии ужимаются данные за счёт утраты избыточной информации, плохоразличимой или неслышимой ухом человека, и, как следствие, некоторого снижения качества записи. Однако сразу оценить существенность таких потерь и понять их суть не очень-то просто. Но сегодня мы постараемся выяснить, в чём же там дело и благодаря чему вообще возможен подобный процесс сжатия данных в десятки раз…
Пора снять завесу, отворить дверцу и воочию взглянуть на таинственный алгоритм будоражащий умы и сердца, добро пожаловать на сеанс с разоблачением!

Несжатый аудиопоток — это массив целых чисел (C# short), к примеру, поступающий из буфера микрофона. Он представляет собой дискретный набор значений-амплитуд аналогового сигнала, взятых через равные промежутки времени (то есть с определённой частотой дискретизации и квантованием по уровню).
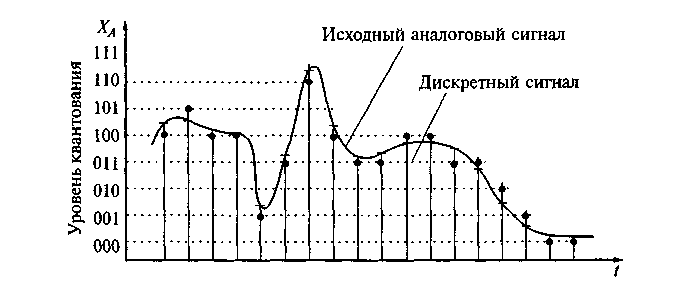
* для простоты здесь и далее будем рассматривать классический моносигнал
Если сразу записывать этот массив в файл, то даже короткий временной интервал получится весьма объёмным. Понятно, что, по всей видимости, в таком потоковом сигнале содержится много избыточных данных, поэтому резонно возникает вопрос, как отобрать нужное и удалить излишнее? Ответ на него прост и суров — использовать преобразование Фурье.
Да, именно то самое, о котором регулярно толкуют в технических университетах и которое, мы успешно успеваем позабыть. Однако это не беда — изучаем вводную презентацию и читаем статью, где вопрос рассматривается более чем подробно. Нам же потребуется лишь сам алгоритм размером всего в 32 строки кода на языке C#.
Преобразование применяется к небольшим порциям сигнала — кадрам с числом отсчётов кратным степени двойки, что обычно составляет 1024, 2048, 4096. При стандартной частоте дискретизации в 44100 Гц, которая согласно теореме Котельникова — Найквиста — Шеннона позволяет без искажений восстанавливать оригинальный сигнал с максимальной частотой в спектре до 22050 Гц, что соответствует максимальному частотному порогу слышимости человеческого уха, эти отрывки по длительности эквивалентны примерно 23, 46 и 93 мс соответственно. После чего мы получаем массив комплексных чисел (той же длины, что и кадр), который содержит информацию о фазовом и частотном спектрах данного фрагмента сигнала. Полученный массив состоит из двух зеркальных частей-копий, поэтому реальной информативностью обладает лишь половина его элементов.
На этом этапе как раз мы можем убрать информацию о тихих частотах, сохранив лишь громкие, например, в виде словаря, а во время воспроизведения восстановить утраченные элементы, заменив их на нулевые, после чего выполнить обратное преобразование Фурье и получить пригодный для воспроизведения сигнал. Именно на этом принципе зиждется работа огромного числа аудиокодеков, поскольку описанная операция даёт возможность производить компрессию в десятки и даже сотни раз (!). Безусловно, способ записи информации в файл тоже вносит свои коррективы в результирующий размер и далеко не лишним будет дополнительное использование алгоритмов архивирования без потерь, но наиболее весомый вклад обеспечивает именно заглушение неслышимых частот.
Поначалу не верится, что таким тривиальным образом можно достичь столь значимых степеней сжатия, но если взглянуть на спектральную картинку в линейном частотном масштабе, а не логарифмическом, то сразу станет ясно, что в реальном спектре обычно присутствует лишь узкий набор гармоник, несущих полезную информацию, а всё остальное — лёгкий шум, который лежит за пределами слышимости. И, как это ни парадоксально, при малых степенях сжатия сигнал не портится для восприятия, а наоборот лишь очищается от шума, то есть идеализируется!
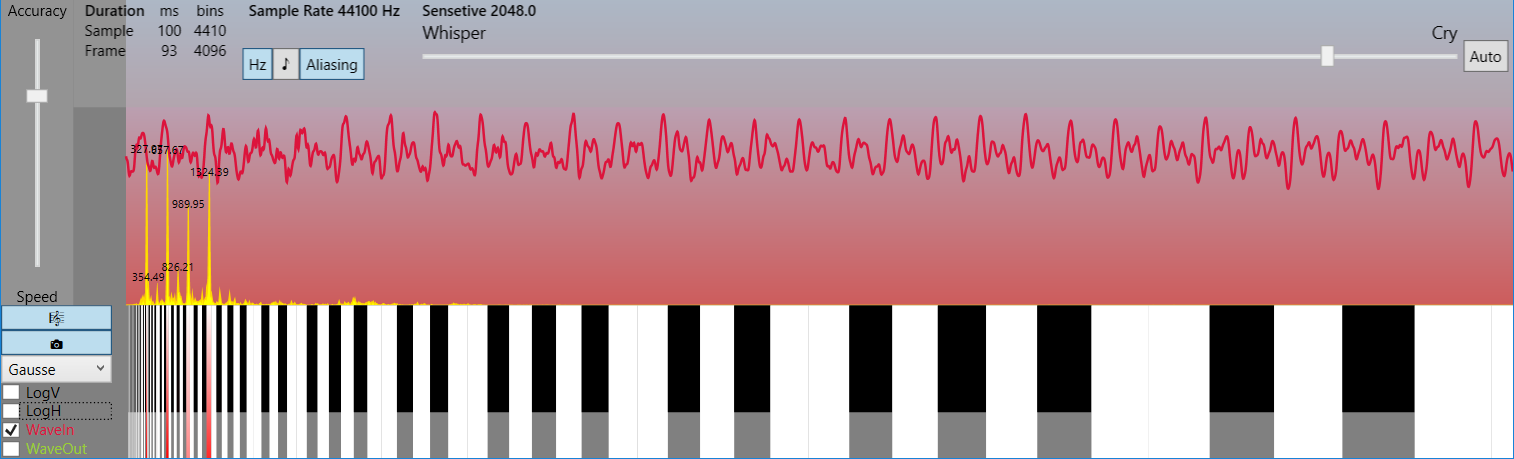
* на картинках отображён кадр в 4096 отсчёта (93 мс) и спектр частот до 22050 Гц (см. LimitFrequency в исходных кодах). Это пример демонстрирует, насколько мало несущих гармоник в реальных сигналах
Чтобы не быть голословным предлагаю протестировать демо приложение (Rainbow Framework), где алгоритм сжатия тривиально прост, но вполне работоспособен. Заодно можно оценить искажения, которые возникают в зависимости от степени сжатия, а также изучить способы визуализации звука и многое другое…
Да, конечно, существуют головоломные алгоритмы учитывающие психо-акустическую модель восприятия, вероятность появления тех или иных частот в спектре и прочее и прочее, но все они помогают лишь отчасти улучшить показатели при сохранении достойного качества, в то время как львиная доля компрессии достигается таким нехитрым способом, который на языке C# занимает буквально лишь несколько строк.
Итак, общая схема компрессии следующая:
1. Разбиение сигнала на амплитудно-временные кадры*
2. Прямое преобразование Фурье — получение амплитудно-частотных кадров
3. Полное заглушение тихих частот и дополнительная опциональная обработка
4. Запись данных в файл
* часто кадры частично перекрывают друг друга, что помогает избежать щелчков, когда сигнал определённой гармоники начинается или оканчивается в одном кадре, но всё ещё слаб и будет заглушен в нём, хотя в другом кадре его звучание набирает полную силу и не заглушается. Из-за чего в зависимости от фазы синусоиды возможен резкий скачок амплитуды на границах неперекрытых кадров, воспринимаемый как пощёлкивание.
Обратный процесс включает такие этапы:
1. Чтение файла
2. Восстановление амплитудно-частотных кадров
3. Обратное преобразование Фурье — получение амплитудно-временных кадров
4. Формирование сигнала из амплитудно-временных кадров
Вот и всё. Наверное, вы ожидали чего-то гораздо более сложного?
Ссылки:
1. Вводная презентация
2. Статья по преобразованию Фурье
3. Демо-приложение с исходными кодами (Rainbow Framework)
(резервная ссылка)
Думаю, что для многих людей аудиокомпрессия с потерями напоминает магический чёрный ящик, где удивительно сложным образом с применением математической алхимии ужимаются данные за счёт утраты избыточной информации, плохоразличимой или неслышимой ухом человека, и, как следствие, некоторого снижения качества записи. Однако сразу оценить существенность таких потерь и понять их суть не очень-то просто. Но сегодня мы постараемся выяснить, в чём же там дело и благодаря чему вообще возможен подобный процесс сжатия данных в десятки раз…
Пора снять завесу, отворить дверцу и воочию взглянуть на таинственный алгоритм будоражащий умы и сердца, добро пожаловать на сеанс с разоблачением!

Несжатый аудиопоток — это массив целых чисел (C# short), к примеру, поступающий из буфера микрофона. Он представляет собой дискретный набор значений-амплитуд аналогового сигнала, взятых через равные промежутки времени (то есть с определённой частотой дискретизации и квантованием по уровню).

* для простоты здесь и далее будем рассматривать классический моносигнал
Если сразу записывать этот массив в файл, то даже короткий временной интервал получится весьма объёмным. Понятно, что, по всей видимости, в таком потоковом сигнале содержится много избыточных данных, поэтому резонно возникает вопрос, как отобрать нужное и удалить излишнее? Ответ на него прост и суров — использовать преобразование Фурье.
Да, именно то самое, о котором регулярно толкуют в технических университетах и которое, мы успешно успеваем позабыть. Однако это не беда — изучаем вводную презентацию и читаем статью, где вопрос рассматривается более чем подробно. Нам же потребуется лишь сам алгоритм размером всего в 32 строки кода на языке C#.
public static Complex[] DecimationInTime(this Complex[] frame, bool direct)
{
if (frame.Length == 1) return frame;
var frameHalfSize = frame.Length >> 1; // frame.Length/2
var frameFullSize = frame.Length;
var frameOdd = new Complex[frameHalfSize];
var frameEven = new Complex[frameHalfSize];
for (var i = 0; i < frameHalfSize; i++)
{
var j = i << 1; // i = 2*j;
frameOdd[i] = frame[j + 1];
frameEven[i] = frame[j];
}
var spectrumOdd = DecimationInTime(frameOdd, direct);
var spectrumEven = DecimationInTime(frameEven, direct);
var arg = direct ? -DoublePi / frameFullSize : DoublePi / frameFullSize;
var omegaPowBase = new Complex(Math.Cos(arg), Math.Sin(arg));
var omega = Complex.One;
var spectrum = new Complex[frameFullSize];
for (var j = 0; j < frameHalfSize; j++)
{
spectrum[j] = spectrumEven[j] + omega * spectrumOdd[j];
spectrum[j + frameHalfSize] = spectrumEven[j] - omega * spectrumOdd[j];
omega *= omegaPowBase;
}
return spectrum;
}
Преобразование применяется к небольшим порциям сигнала — кадрам с числом отсчётов кратным степени двойки, что обычно составляет 1024, 2048, 4096. При стандартной частоте дискретизации в 44100 Гц, которая согласно теореме Котельникова — Найквиста — Шеннона позволяет без искажений восстанавливать оригинальный сигнал с максимальной частотой в спектре до 22050 Гц, что соответствует максимальному частотному порогу слышимости человеческого уха, эти отрывки по длительности эквивалентны примерно 23, 46 и 93 мс соответственно. После чего мы получаем массив комплексных чисел (той же длины, что и кадр), который содержит информацию о фазовом и частотном спектрах данного фрагмента сигнала. Полученный массив состоит из двух зеркальных частей-копий, поэтому реальной информативностью обладает лишь половина его элементов.
На этом этапе как раз мы можем убрать информацию о тихих частотах, сохранив лишь громкие, например, в виде словаря, а во время воспроизведения восстановить утраченные элементы, заменив их на нулевые, после чего выполнить обратное преобразование Фурье и получить пригодный для воспроизведения сигнал. Именно на этом принципе зиждется работа огромного числа аудиокодеков, поскольку описанная операция даёт возможность производить компрессию в десятки и даже сотни раз (!). Безусловно, способ записи информации в файл тоже вносит свои коррективы в результирующий размер и далеко не лишним будет дополнительное использование алгоритмов архивирования без потерь, но наиболее весомый вклад обеспечивает именно заглушение неслышимых частот.
Поначалу не верится, что таким тривиальным образом можно достичь столь значимых степеней сжатия, но если взглянуть на спектральную картинку в линейном частотном масштабе, а не логарифмическом, то сразу станет ясно, что в реальном спектре обычно присутствует лишь узкий набор гармоник, несущих полезную информацию, а всё остальное — лёгкий шум, который лежит за пределами слышимости. И, как это ни парадоксально, при малых степенях сжатия сигнал не портится для восприятия, а наоборот лишь очищается от шума, то есть идеализируется!

* на картинках отображён кадр в 4096 отсчёта (93 мс) и спектр частот до 22050 Гц (см. LimitFrequency в исходных кодах). Это пример демонстрирует, насколько мало несущих гармоник в реальных сигналах
Чтобы не быть голословным предлагаю протестировать демо приложение (Rainbow Framework), где алгоритм сжатия тривиально прост, но вполне работоспособен. Заодно можно оценить искажения, которые возникают в зависимости от степени сжатия, а также изучить способы визуализации звука и многое другое…
var fftComplexFrequencyFrame = inputComplexTimeFrame.DecimationInTime(true);
var y = 0;
var original = fftComplexFrequencyFrame.ToDictionary(c => y++, c => c);
var compressed = original.OrderByDescending(p => p.Value.Magnitude).Take(CompressedFrameSize).ToList();
Да, конечно, существуют головоломные алгоритмы учитывающие психо-акустическую модель восприятия, вероятность появления тех или иных частот в спектре и прочее и прочее, но все они помогают лишь отчасти улучшить показатели при сохранении достойного качества, в то время как львиная доля компрессии достигается таким нехитрым способом, который на языке C# занимает буквально лишь несколько строк.
Итак, общая схема компрессии следующая:
1. Разбиение сигнала на амплитудно-временные кадры*
2. Прямое преобразование Фурье — получение амплитудно-частотных кадров
3. Полное заглушение тихих частот и дополнительная опциональная обработка
4. Запись данных в файл
* часто кадры частично перекрывают друг друга, что помогает избежать щелчков, когда сигнал определённой гармоники начинается или оканчивается в одном кадре, но всё ещё слаб и будет заглушен в нём, хотя в другом кадре его звучание набирает полную силу и не заглушается. Из-за чего в зависимости от фазы синусоиды возможен резкий скачок амплитуды на границах неперекрытых кадров, воспринимаемый как пощёлкивание.
Обратный процесс включает такие этапы:
1. Чтение файла
2. Восстановление амплитудно-частотных кадров
3. Обратное преобразование Фурье — получение амплитудно-временных кадров
4. Формирование сигнала из амплитудно-временных кадров
Вот и всё. Наверное, вы ожидали чего-то гораздо более сложного?
Ссылки:
1. Вводная презентация
2. Статья по преобразованию Фурье
3. Демо-приложение с исходными кодами (Rainbow Framework)
(резервная ссылка)