How to become an author
Search
Write a publication
Pull to refresh

Рисуем эллиптические кривые с помощью SQL

Reading time5 min
Views13K
SQL*Entertaining tasksCryptography*Mathematics*
Преимущество подхода на основе эллиптических кривых в сравнении с задачей факторизации числа, используемой в RSA, или задачей целочисленного логарифмирования, применяемой в алгоритме Диффи-Хеллмана и в DSS, заключается в том, что в данном случае обеспечивается эквивалентная защита при меньшей длине ключа.

В общем случае уравнение эллиптической кривой Е в поле действительных чисел R имеет вид:

— y^2+a1*x*y+a3*y = x^3+a2*x^2+a4*x+a6

или в случае конечного кольца вычетов Z|n:

— y^2+a1*x*y+a3*y = x^3+a2*x^2+a4*x+a6 mod N

Поставим перед собой задачу визуализации эллиптической кривой.

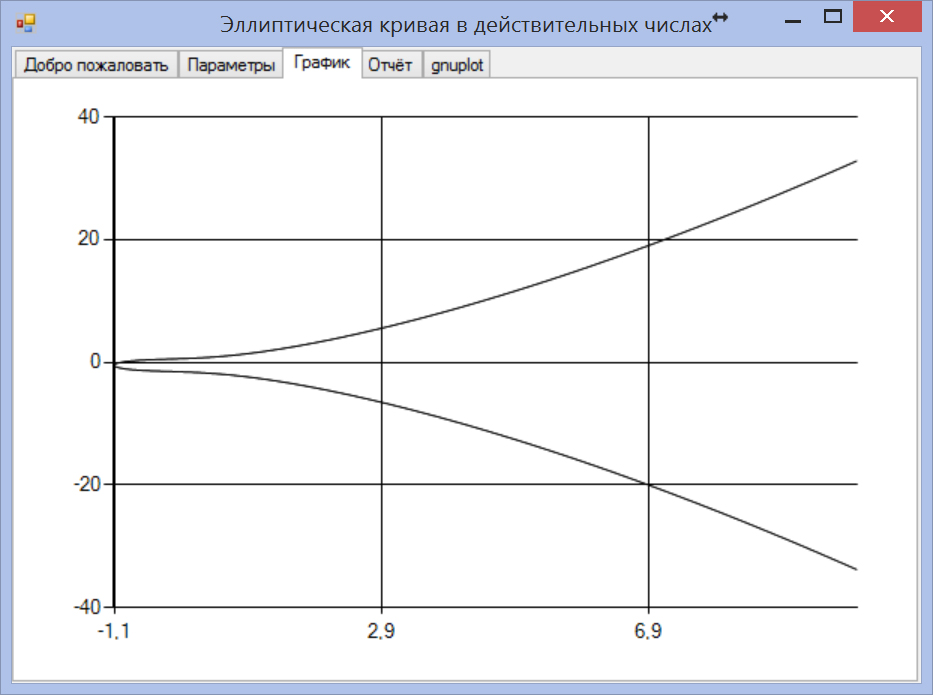
Эллиптическая кривая Е в поле действительных чисел R


Если эллиптическая кривая Е рассматривается в поле действительных чисел R, то построение графика можно описать, используя только знания алгебры и геометрии старших классов школы

аргументы N a1 a2 a3 a4 a6 xmin xmax
  1. Выбираем диапазон [xmin — xmax] аргумента x
  2. Отмечаем на выбранном диапазоне аргумента x необходимое число значений x1,...,xN
  3. Каждое из значений x1,...,xN подставляем в уравнение y^2+a1*x*y+a3*y = x^3+a2*x^2+a4*x+a6 и получаем обычное квадратичное уравнение аргумента y
  4. Находим корни квадратичного уравнения аргумента y
  5. Если квадратичное уравнение аргумента y имеет решения, то добавляем две точки на график
  6. Соединяем линиями все «верхние» точки на графике и все «нижние» точки на графике


— a=a(x)=1
— b=b(x)=a1*x+a3
— c=c(x)=-(x^3+a2*x^2+a4*x+a6)

— ayy+by+c=0
— D=bb-4ac
— y1=(-b-sqrt(D))/(2a)
— y2=(-b+sqrt(D))/(2a)

Реализация


        private void button1_Click(object sender, EventArgs e)
        {
            LockForm();

            // Параметры эллиптической кривой
            double a1 = GetA1();
            double a2 = GetA2();
            double a3 = GetA3();
            double a4 = GetA4();
            double a6 = GetA6();

            // Диапазон изменения переменной X и количество интервалов
            double xmin = GetXmin();
            double xmax = GetXmax();
            ulong n = GetN();

            // http://stackoverflow.com/questions/10622674/chart-creating-dynamically-in-net-c-sharp
            var series1 = new Series
            {
                Name = "Series1",
                Color = Color.Black,
                IsVisibleInLegend = false,
                IsXValueIndexed = true,
                ChartType = SeriesChartType.Line
            };

            var series2 = new Series
            {
                Name = "Series2",
                Color = Color.Black,
                IsVisibleInLegend = false,
                IsXValueIndexed = true,
                ChartType = SeriesChartType.Line
            };

            var sb = new StringBuilder();
            var sb1 = new StringBuilder();
            sb.AppendLine("y^2+a1*x*y+a3*y = x^3+a2*x^2+a4*x+a6");
            sb.AppendLine("a1=" + a1);
            sb.AppendLine("a2=" + a2);
            sb.AppendLine("a3=" + a3);
            sb.AppendLine("a4=" + a4);
            sb.AppendLine("a6=" + a6);
            sb.AppendLine();
            sb.AppendLine("# X Y1 Y2");
            sb1.AppendLine("# X Y1 Y2");
            for (ulong i = 0; i <= n; i++)
            {
                double x = (xmin*(n - i) + xmax*i)/n;

                // Рассчитываем параметры квадратичного уравнения для данного X
                const double a = 1;
                double b = a1*x + a3;
                double c = -(x*x*x + a2*x*x + a4*x + a6);

                // По формуле за шестой класс средней школы вычисляем решение квадратичного уравнения
                double d = b*b - 4*a*c;
                if (d < 0) continue;

                double y1 = (-b - Math.Sqrt(d))/(2*a);
                double y2 = (-b + Math.Sqrt(d))/(2*a);

                series1.Points.AddXY(x, y1);
                series2.Points.AddXY(x, y2);

                sb.AppendLine(x + " " + y1 + " " + y2);
                sb1.AppendLine(x + " " + y1 + " " + y2);
            }

            // Выдаём отчёт о проделанной работе
            SetChart(series1, series2);
            SetReport(sb.ToString());
            SetReport1(sb1.ToString());

            UnlockForm();
            ActivatePage(2);
        }

Результат


Эллиптическая кривая Е в поле действительных чисел R

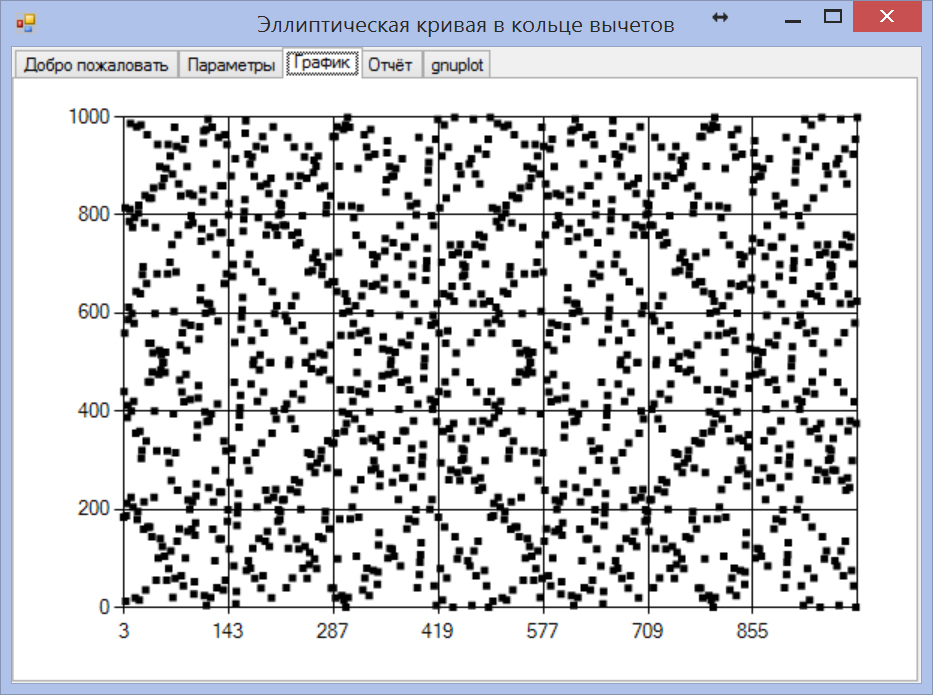
Эллиптическая кривая Е в кольце вычетов Z|n


Если эллиптическая кривая Е рассматривается для конечного кольца вычетов Z|n, то задача визуализации эллиптической кривой представляется более сложной задачей.
В этом случае можно предложить стандартный легко программируемый алгоритм rendezvous соединения значений левой и правой частей уравнения эллиптической кривой Е:

— аргументы N a1 a2 a3 a4 a6

  1. кэшировать в таблицах значения левой и правой частей уравнения
  2. построить индексы для колонок таблиц
  3. сделать объединение таблиц по вычисленными значениям
  4. полученные точки после объединения таблиц изобразить на графике.


Для работы с кэшированными значения левой и правой частей уравнения эллиптической кривой Е, будем использовать DBMS, которая позволит наиболее оптимально выполнить работу по индексации колонок таблиц и объединению этих таблиц.

t1
x key1 = x^3+a2*x^2+a4*x+a6 mod N
1…
2…
3…
…
N rN

t2
y key2 = y^2+a3*y mod N
1…
2…
3…
…
N lN

t3
x y key3=a1*x*y mod N
1 1…
1 2…
…
N N…

if(a1!=0 mod N) select t1.x,t2.y from t1, t2, t3 where (key1=key2+key3 or key1+N=key2+key3) and t1.x=t3.x and t2.y=t3.y
if(a1==0 mod N) select t1.x,t2.y from t1, t2 where key1=key2

Реализация


— DBMS — SQLite
        private void button1_Click(object sender, EventArgs e)
        {
            LockForm();

            // Параметры кольца вычетов Z|n
            var n = GetN();

            // Параметры эллиптической кривой
            var a1 = GetA1();
            var a2 = GetA2();
            var a3 = GetA3();
            var a4 = GetA4();
            var a6 = GetA6();

            // http://stackoverflow.com/questions/9173485/how-can-i-create-an-in-memory-sqlite-database
            var connection = new SQLiteConnection("Data Source=:memory:");
            connection.Open();

            // Создаём таблицы
            string[] sqls1 =
            {
                "CREATE TABLE t1 (x INTEGER , key1 INTEGER )",
                "CREATE TABLE t2 (y INTEGER , key2 INTEGER )",
                "CREATE TABLE t3 (x INTEGER , y INTEGER , key3 INTEGER )"
            };

            foreach (var sql in sqls1)
                new SQLiteCommand(sql, connection).ExecuteNonQuery();

            // Заполняем таблицы начальными значениями
            for (ulong x = 0; x < n; x++)
            {
                var x2 = (x*x)%n;
                var x3 = (x2*x)%n;
                var a2X2 = (a2*x2)%n;
                var a4X = (a4*x)%n;
                var key1 = (x3 + a2X2 + a4X + a6)%n;
                var sql = string.Format("INSERT INTO t1 (x, key1) VALUES ({0},{1})", x, key1);
                new SQLiteCommand(sql, connection).ExecuteNonQuery();
            }

            for (ulong y = 0; y < n; y++)
            {
                var y2 = y*y%n;
                var a3Y = (a3*y)%n;
                var key2 = (y2 + a3Y)%n;
                var sql = string.Format("INSERT INTO t2 (y, key2) VALUES ({0},{1})", y, key2);
                new SQLiteCommand(sql, connection).ExecuteNonQuery();
            }

            if ((a1%n) != 0)
                for (ulong x = 0; x < n; x++)
                {
                    var a1X = (a1*x)%n;
                    for (ulong y = 0; y < n; y++)
                    {
                        var key3 = (a1X*y)%n;
                        var sql = string.Format("INSERT INTO t3 (x, y, key3) VALUES ({0},{1},{2})", x, y, key3);
                        new SQLiteCommand(sql, connection).ExecuteNonQuery();
                    }
                }

            // Создаём индексы для таблиц
            string[] sqls2 =
            {
                "CREATE INDEX t1key1 ON t1 (key1)",
                "CREATE INDEX t2key2 ON t2 (key2)",
                "CREATE INDEX t3key3 ON t3 (key3)",
                "CREATE UNIQUE INDEX t1x ON t1 (x)",
                "CREATE UNIQUE INDEX t2y ON t2 (y)",
                "CREATE INDEX t3x ON t3 (x)",
                "CREATE INDEX t3y ON t3 (y)"
            };

            foreach (var sql in sqls2)
                new SQLiteCommand(sql, connection).ExecuteNonQuery();

            // http://stackoverflow.com/questions/10622674/chart-creating-dynamically-in-net-c-sharp
            var series1 = new Series
            {
                Name = "Series1",
                Color = Color.Black,
                IsVisibleInLegend = false,
                IsXValueIndexed = true,
                ChartType = SeriesChartType.Point
            };

            // Выполняем JOIN запрос и получаем результаты
            // Чем дороже DBMS тем лучше алгоритмы она использует для оптимизации запросов
            var select = ((a1%n) == 0)
                ? "SELECT t1.x,t2.y FROM t1, t2 WHERE key1=key2"
                : "SELECT t1.x,t2.y FROM t1, t2, t3 WHERE (key1=key2+key3 or key1+" + n +
                  "=key2+key3) AND t1.x=t3.x AND t2.y=t3.y";
            var reader = new SQLiteCommand(select, connection).ExecuteReader();
            var sb = new StringBuilder();
            var sb1 = new StringBuilder();
            sb.AppendLine("y^2+a1*x*y+a3*y = x^3+a2*x^2+a4*x+a6 mod n");
            sb.AppendLine("n=" + n);
            sb.AppendLine("a1=" + a1);
            sb.AppendLine("a2=" + a2);
            sb.AppendLine("a3=" + a3);
            sb.AppendLine("a4=" + a4);
            sb.AppendLine("a6=" + a6);
            sb.AppendLine();
            sb.AppendLine("# X Y");
            sb1.AppendLine("# X Y");
            while (reader.Read())
            {
                var x = Convert.ToInt32(reader[0]);
                var y = Convert.ToInt32(reader[1]);
                series1.Points.AddXY(x, y);
                sb.AppendLine(x + " " + y);
                sb1.AppendLine(x + " " + y);
            }

            // Выдаём отчёт о проделанной работе
            SetChart(series1);
            SetReport(sb.ToString());
            SetReport1(sb1.ToString());
            connection.Close();

            UnlockForm();
            ActivatePage(2);
        }

Результат


Эллиптическая кривая Е в кольце вычетов Z|n

Что и требовалось доказать

Исходные коды программ доступны по адресу https://github.com/dprotopopov/mssove3
Tags:
Hubs:
Total votes 13: ↑11 and ↓2+9
Comments13
-2
Karma
0
Rating
Дмитрий Про @dprotopopov

Граф О'ман

Send message
Github

Articles

Your account

Sections

Information

Services

Support
© 2006–2024, Habr