PodnimatelPingvinov Feb 8 2017 at 18:11

Метод рекурсивной координатной бисекции для декомпозиции расчетных сеток

8 min

9.5K

Введение

Расчетные сетки широко применяются при решении численных задач с помощью методов конечных разностей. Качество построения такой сетки в значительной степени определяет успех в решении, поэтому иногда сетки достигают огромных размеров. В этом случае на помощь приходят многопроцессорные системы, ведь они позволяют решить сразу 2 задачи:

Повысить скорость работы программы.
Работать с сетками такого размера, который не помещается в оперативной памяти одного процессора.

При таком подходе сетка, покрывающая расчетную область, разбивается на множество доменов, каждый из которых обрабатывается отдельным процессором. Основная проблема здесь заключается в «честности» разбиения: нужно выбрать такую декомпозицию, при которой вычислительная нагрузка распределена равномерно между процессорами, а накладные расходы, вызванные дублированием вычислений и необходимостью передачи данных между процессорами, малы.

Характерный пример двумерной расчетной сетки приведен на первой картинке. Она описывает пространство вокруг крыла и закрылка самолета, узлы сетки сгущаются к мелким деталям. Несмотря на визуальное различие в размерах разноцветных зон, каждая из них содержит примерно одинаковое число узлов, т.е. можно говорить о хорошей декомпозиции. Именно эту задачу мы и будем решать.

Примечание: поскольку в алгоритме активно используется параллельная сортировка, то для понимания статьи настоятельно рекомендуется знать что такое "Сеть обменной сортировки со слиянием Бэтчера".

Постановка задачи

Для простоты будем считать, что процессоры у нас одноядерные. Еще раз, чтобы не было путаницы:
1 процессор = 1 ядро. Вычислительная система с распределенной памятью, поэтому будем использовать технологию MPI. На практике в таких системах процессоры многоядерные, а значит для максимально эффективного использования вычислительных ресурсов следует также использовать треды.

Сетки мы ограничим лишь регулярными двумерными, т.е. такими, в которых узел с индексами (i, j) соединен с соседними существующими по i, j узлами: (i-1, j), (i+1, j), (i, j-1), (i, j+1). Как нетрудно заметить, на верхней картинке сетка не регулярна, примеры регулярных сеток изображены ниже:

Благодаря этому можно очень компактно хранить топологию сетки, что позволяет существенно снизить как расход памяти, так и время работы программы (ведь нужно пересылать куда меньше данных по сети между процессорами).

На вход программе поступают 3 аргумента:

n1, n2 — размеры двумерной сетки.
k — число доменов (частей) на которое требуется разбить сетку.

Инициализация координат происходит внутри программы и нам, вообще говоря, не важно как это происходит (можно посмотреть как это сделано в исходном коде, ссылка на который есть в конце статьи, но подробно останавливаться на этом я не буду).

Один узел сетки мы будем хранить в следующей структуре:

struct Point{
    float coord[2]; // 0 - x, 1 - y
    int index;
};

Помимо координат точки здесь еще есть индекс узла, который имеет 2 назначения. Во-первых, его одного достаточно для восстановления топологии сетки. Во-вторых, с помощью него можно отличать фиктивные элементы от нормальных (например, у фиктивных элементов значение этого поля установить равным -1). Про то, что это за фиктивные элементы и зачем они нужны, будет подробно рассказано далее.

Сама сетка хранится в массиве Point P[n1*n2], где узел с индексами (i, j) находится в P[i*n2+j]. В результате работы программы число вершин в доменах должно быть равно с точностью до одной вершины величине (n1*n2/k).

Алгоритм решения

Процедура рекурсивной координатной бисекции состоит из 3 шагов:

Сортировка массива узлов вдоль одной из координатных осей (в двумерном случае вдоль x или y).
Разбиение отсортированного массива на 2 части.
Рекурсивный запуск процедуры для полученных подмассивов.

Базисом рекурсии здесь является случай k = 1 (остался 1 домен). Происходит примерно следующее:

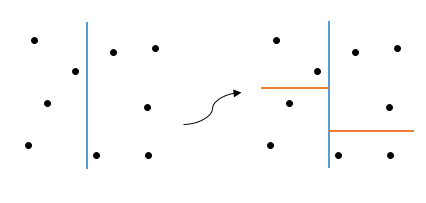
А может и так:

Откуда взялась неоднозначность? Нетрудно заметить, что я никак не оговорил критерий выбора оси, именно отсюда и появились разные варианты (на 1 шаге в первом случае сортировка проходит по оси x, а во втором по y). Так как выбрать ось?

Рандомно.

Дешево и сердито, но занимает всего 1 строчку кода и требует минимум времени. В демонстрационной программе, для простоты, используется похожий метод (на самом деле там просто на каждом шаге ось меняется на противоположную, но с концептуальной точки зрения это одно и то же). Если хочется написать хорошо — не делайте так.
Из геометрических соображений.

Минимизируется длина проводимого разреза (в общем случае разрез — это гиперплоскость, поэтому в многомерном случае корректнее говорить о площади). Для этого нужно выбрать точки с минимальными и максимальными значениями координат после чего измерить длину на основании какой-либо метрики. Затем достаточно сравнить полученные длины и выбрать соответствующую ось. Конечно, здесь легко подобрать контрпример:

Вертикальный разрез короче, но пересекает 9 ребер, в то время как более длинный горизонтальный разрез пересекает всего 4 ребра. Причем такие сетки не являются вырожденным случаем, а используются в задачах. Однако этот вариант представляет собой баланс между скоростью и качеством разбиения: здесь требуется не так много вычислений, как в третьем варианте, но качество разбиения как правило лучше, чем в первом случае.
Минимизировать число разрезанных ребер.

Разрезанное ребро — это ребро, соединяющее вершины из разных доменов. Таким образом, если минимизировать это число, то домены получаются как можно более «автономными», поэтому можно говорить о высоком качестве разбиения. Так, на картинке выше этот алгоритм выберет горизонтальную ось. Платить за это приходится скоростью, ведь нужно поочередно отсортировать массив вдоль каждой из осей, а затем посчитать число разрезанных ребер.

Еще стоит оговорить как разбивать массив. Пусть m = n1*n2 (общее число узлов и длина массива P), а k — число доменов (как и прежде). Тогда мы пытаемся разделить число доменов пополам, а затем делим массив в таком же соотношении. В виде формул:

int k1 = (k + 1) / 2;
int k2 = k - k1;
int m1 = m * (k1 / (double)k);
int m2 = m - m1;

На примере: разбить 9 элементов на 3 домена (m = 9, k = 3). Тогда сначала массив разделится в соотношении 6 к 3, а затем массив из 6 элементов разобьется пополам. В результате мы получим 3 домена по 3 элемента в каждом. То что надо.

Примечание: некоторые могут спросить, зачем в выражении для m1 нужна вещественная арифметика, ведь без ее использования получится тот же результат? Все дело в переполнении, например, при разбиении сетки 10000х10000 на 100 доменов m * k1 = 10¹⁰, что выходит за границы диапазона int. Будьте внимательны!

Последовательный алгоритм

Разобравшись с теорией, можно переходить к реализации. Для сортировки будем использовать функцию qsort() из стандартной библиотеки языка Си. Наша функция будет принимать 6 аргументов:

void local_decompose(Point *a, int *domains, int domain_start, int k, int array_start, int n);

Здесь:

a — исходная сетка.
domains — выходной массив, в котором хранятся номера доменов для узлов сетки (имеет такую же длину что и массив a).
domain_start — начальный индекс доступных номеров доменов.
k — число доступных элементов.
array_start — начальный элемент в массиве.
n — число элементов в массиве.

Первым делом напишем базис рекурсии:

void local_decompose(Point *a, int *domains, int domain_start, int k, int array_start, int n)
{
    if(k == 1){
        for(int i = 0; i < n; i++)
            domains[array_start + i] = domain_start;
        return;
    }

Если у нас остался всего 1 домен, то мы помещаем все доступные узлы сетки в него. Затем мы выбираем ось и сортируем сетку вдоль нее:

    axis = !axis;
    qsort(a + array_start, n, sizeof(Point), compare_points);

Ось можно выбрать одним из предложенных выше способов. В этом примере, как говорилось ранее, она просто меняется на противоположную. Здесь axis — это глобальная переменная, которая используется в функции сравнения элементов compare_points():

int compare_points(const void *a, const void *b)
{
    if(((Point*)a)->coord[axis] < ((Point*)b)->coord[axis]){
        return -1;
    }else if(((Point*)a)->coord[axis] > ((Point*)b)->coord[axis]){
        return 1;
    }else{
        return 0
    }
}

Теперь нам осталось разбить доступные нам домены и узлы сетки по соответствующим формулам:

    int k1 = (k + 1) / 2;
    int k2 = k - k1;
    int n1 = n * (k1 / (double)k);
    int n2 = n - n1;

И написать рекурсивный вызов:

    local_decompose(a, domains, domain_start, k1, array_start, n1);
    local_decompose(a, domains, domain_start + k1, k2, array_start + n1, n2);
}

Вот и все. Полностью исходный код функции local_decompose() доступен на гитхабе.

Параллельный алгоритм

Несмотря на то что алгоритм остался тем же, его параллельная реализация куда сложнее. Я связываю это с двумя основными причинами:

1) В системе используется распределенная память, поэтому каждый процессор хранит лишь свою часть данных не видя всю сетку целиком. Из-за этого при разделении массива приходится перераспределять элементы.

2) В качестве алгоритма сортировки используется параллельная сортировка Бетчера, для работы которой необходимо, чтобы на каждом процессоре было одинаковое число элементов.

Сначала разберемся со второй проблемой. Решение тривиально — нужно ввести фиктивные элементы, о которых вскользь упоминалось ранее. Вот тут нам и пригодится поле index в структуре Point. Делаем его равным -1 — и перед нами фиктивный элемент! Вроде все отлично, но этим решением мы существенно усугубили первую проблему. В общем случае на этапе разбиения массива на 2 части становится невозможно определить не только сам разбивающий элемент, но даже процессор, на котором он находится. Поясню это на примере: пусть у нас есть 9 элементов (сетка 3х3), которые нужно разбить на 3 домена на 4 процессорах, т.е. n = 9, k = 3, p = 4. Тогда после сортировки фиктивные элементы могут оказаться в любом месте (на картинке зеленым обозначены узлы сетки, а красным — фиктивные элементы):

В этом случае первый элемент второго массива будет посередине на 2 процессоре. Но если фиктивные элементы расположились иначе, то все изменится:

Здесь уже разбивающий элемент оказался на последнем процессоре. Чтобы избежать этой неоднозначности, применим небольшой хак: сделаем координаты фиктивных элементов максимально возможными (поскольку в программе они хранятся в переменных типа float, то значение будет FLT_MAX). В результате фиктивные элементы всегда будут в конце:

На картинке хорошо заметно, что при таком подходе на последних процессорах будут преобладать фиктивные элементы. Эти процессоры будут выполнять бесполезную работу, на каждом шаге рекурсии сортируя фиктивные элементы. Однако теперь определение разбивающего элемента становится тривиальной задачей, он будет находиться на процессоре с номером:

int pc = n1 / elem_per_proc;

И иметь следующий индекс в локальном массиве:

int middle = n1 % elem_per_proc;

Когда разбивающий элемент определен, содержащий его процессор начинает процедуру перераспределения элементов: все элементы до разбивающего он равномерно рассылает процессорам «до» него (т.е. с номерами, меньшими чем у него), при необходимости добавляя фиктивные. У себя отправленные элементы он заменяет на фиктивные. В картинках для n = 15, k = 5, p = 4:

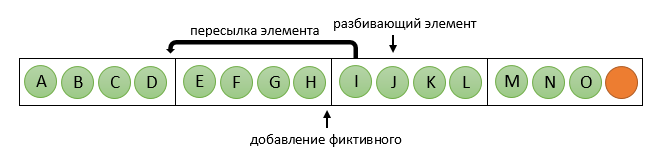
Теперь процессоры с номерами меньше чем pc будут дальше работать с первой частью исходного массива, а остальные, параллельно, со второй частью. При этом в рамках одной группы число элементов на всех процессорах одинаковое (хотя у второй группы оно может быть другим), что позволяет дальше использовать сортировку Бетчера. Не стоит забывать, что возможен случай pc = 0 — тогда достаточно пересылать элементы в «другую сторону», т.е. на процессоры с большими номерами.

Базисом рекурсии в параллельном алгоритме в первую очередь следует считать ситуацию, когда у нас закончились процессоры: случай с k = 1 остается, но скорее является вырожденным, поскольку на практике число доменов как правило больше чем число процессоров.

С учетом всего вышесказанного общая схема функции будет выглядеть так:

Общая схема функции decompose

void decompose(Point **array, int **domains, int domain_start, int k, int n,
        int *elem_per_proc, MPI_Comm communicator)
{
    // инициализация переменных
    int rank, proc_count;
    MPI_Comm_rank(communicator, &rank);
    MPI_Comm_size(communicator, &proc_count);
    // базис рекурсии
    if(proc_count == 1){
        // если закончились процессоры, то запустить последовательный алгоритм
        local_decompose(...);
        return;
    }
    if(k == 1){
        // а если закончились домены, то присвоить оставшийся домен всем доступным элементам
        return;
    }

    // разделение массива на 2 части
    int k1 = (k + 1) / 2;
    int k2 = k - k1;
    int n1 = n * (k1 / (double)k);
    int n2 = n - n1;
    // нахождение разбивающего элемента
    int pc = n1 / (*elem_per_proc);
    int middle = n1 % (*elem_per_proc);
    // разделение процессоров на 2 группы, которые будут параллельно
    // работать с новыми подмассивами
    int color;
    if(pc == 0)
        color = rank > pc ? 0 : 1;
    else
        color = rank >= pc ? 0 : 1;
    MPI_Comm new_comm;
    MPI_Comm_split(communicator, color, rank, &new_comm);

    // выбор оси для сортировки и сама параллельная сортировка
    axis = ...
    sort_array(*array, *elem_per_proc, communicator);

    if(pc == 0){
        // перераспределение элементов на процессоры с большими номерами
        // и соответствующий рекурсивный вызов
        return;
    }
    // перераспределение элементов на процессоры с меньшими номерами
    // и немного другой рекурсивный вызов
    if(rank < pc)
        decompose(array, domains, domain_start, k1, n1, elem_per_proc, new_comm);
    else
        decompose(array, domains, domain_start + k1, k2, n2, elem_per_proc, new_comm);
}

Заключение

Рассмотренная реализация алгоритма обладает рядом недостатков, но в то же время имеет и неоспоримое преимущество — она работает! Исходный код программы можно найти на гитхабе. Там же расположена вспомогательная утилита для просмотра результатов. При подготовке этой статьи использовались материалы книги М. В. Якобовского «Введение в параллельные методы решения задач».

Tags:

Hubs: