Автоэнкодеры в Keras, Часть 5: GAN(Generative Adversarial Networks) и tensorflow / Habr

Содержание

Часть 1: Введение
Часть 2: Manifold learning и скрытые (latent) переменные
Часть 3: Вариационные автоэнкодеры (VAE)
Часть 4: Conditional VAE
Часть 5: GAN (Generative Adversarial Networks) и tensorflow
Часть 6: VAE + GAN

(Из-за вчерашнего бага с перезалитыми картинками на хабрасторейдж, случившегося не по моей вине, вчера был вынужден убрать эту статью сразу после публикации. Выкладываю заново.)

При всех преимуществах вариационных автоэнкодеров VAE, которыми мы занимались в предыдущих постах, они обладают одним существенным недостатком: из-за плохого способа сравнения оригинальных и восстановленных объектов, сгенерированные ими объекты хоть и похожи на объекты из обучающей выборки, но легко от них отличимы (например, размыты).

Этот недостаток в куда меньшей степени проявляется у другого подхода, а именно у генеративных состязающихся сетей — GAN’ов.

Формально GAN’ы, конечно, не относятся к автоэнкодерам, однако между ними и вариационными автоэнкодерами есть сходства, они также пригодятся для следующей части. Так что не будет лишним с ними тоже познакомиться.

Коротко о GAN

GAN’ы впервые были предложены в статье [1, Generative Adversarial Nets, Goodfellow et al, 2014] и сейчас очень активно исследуются. Наиболее state-of-the-art генеративные модели так или иначе используют adversarial.

Схема GAN:

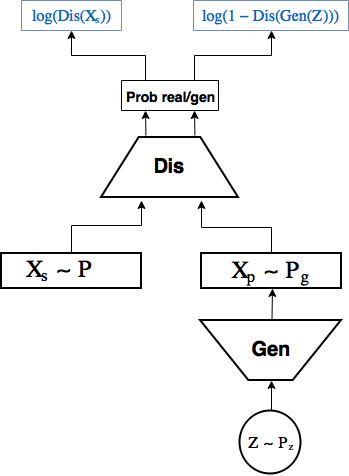
GAN’ы состоят из 2 нейронных сетей:

1-ая — генератор сэмплит случайные числа из какого-то заданного распределения , например и генерируют из них объекты $X_p = G(Z; \theta_g)$ , которые идут на вход второй сети,
2-ая — дискриминатор получает на вход объекты из выборки и созданные генератором , и учится предсказывать вероятность того, что конкретный объект реальный, выдавая скаляр $D(X; \theta_d)$ .

При этом генератор тренируется создавать объекты, который дискриминатор не отличит от реальных.

Рассмотрим процесс обучения GAN.

Генератор и дискриминатор обучаются отдельно, но в рамках одной сети.

Делаем k шагов обучения дискриминатора: за шаг обучения дискриминатора параметры $\theta_d$ обновляются в сторону уменьшения кросс-энтропии:

$\theta_d = \theta_d - \nabla_{\theta_d} \left(\log(D(X_s)) + \log(1 - D(G(Z))) \right)$

Далее шаг обучения генератора: обновляем параметры генератора $\theta_g$ в сторону увеличения логарифма ��ероятности дискриминатору присвоить сгенерированному объекту лейбл реального.

$\theta_g = \theta_g + \nabla_{\theta_g} \log(1 - D(G(Z)))$

Схема обучения:

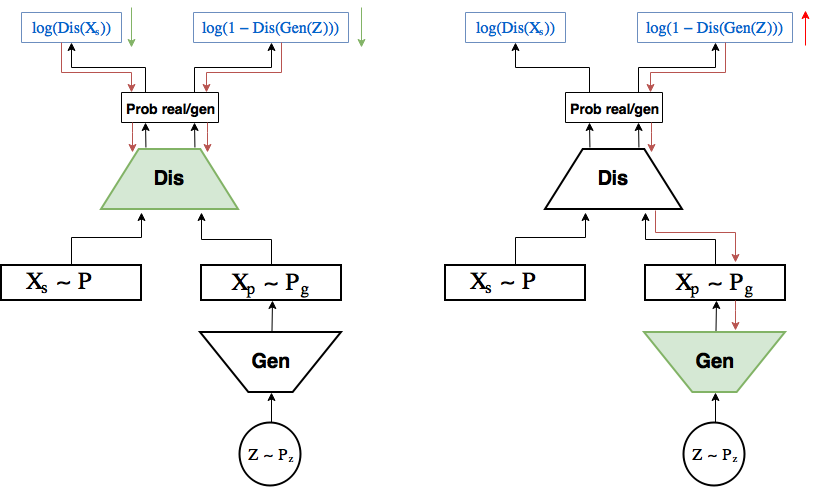
На левой картинке шаг обучения дискриминатора: градиент (красные стрелки) протекает от лосса только до дискриминатора, где обновляются $\theta_d$ (зеленые) в сторону уменьшения лосса. На правой картинке градиент от правой части лосса (ошибка идентификации сгенерированного объекта) протекает до генератора, при этом обновляются только веса генератора $\theta_g$ (зеленые) в сторону увеличения вероятности дискриминатора ошибиться.

Задача, которую решает GAN формулируется так:

$\min_G \max_D \mathbb{E}_{X \sim P}[ \log(D(X))] + \mathbb{E}_{Z \sim P_z}[ \log(1 - D(G(Z)))]$

При заданном генераторе оптимальный дискриминатор выдает вероятность $D^*(X) = \frac{P(X)}{P_g(X) + P(X)},$ что почти очевидно, предлагаю на секунду об этом задуматься.

В [1] показывается, что при достаточной мощности обеих сетей у данной задачи есть оптимум, в котором генератор научился генерировать распределение P_g(X)

, совпадающее с P(X)

, а везде на $X^{}$ дискриминатор выдает вероятность 1/2

Иллюстрация из [1]

Обозначения:

черная точечная кривая — настоящее распределение ,
зеленая — распределение генератора ,
синяя — распределение вероятности $D(X;\theta_d)$ дискриминатора предсказать класс реального объекта,
нижняя и верхняя прямые — множество всех и множество всех , стрелочки олицетворяют отображение $G(Z;\theta_g)$ .

На картинке:

(a) и довольно разные, но дискриминатор неуверенно отличает одно от другого,
(b) дискриминатор после k шагов обучения уже отличает их увереннее,
(с) это позволяет генератору , руководствуясь хорошим градиентом дискриминатора , на границе двух распределений подвинуть ближе к ,
(d) в результате многих повторений шагов (а), (b), (с) совпало с , и дискриминатор более не способен отличать одно от другого: . Точка оптимума достигнута.

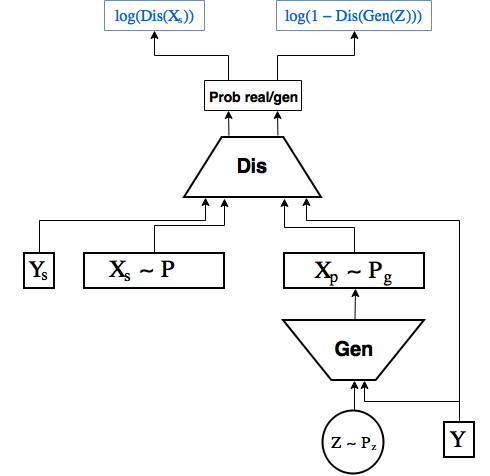
Conditional GAN

Точно как в прошлой части мы сделали Conditional VAE, просто передавая в энкодер и декодер лейбл цифры, здесь мы будем передавать его в генератор и дискриминатор [2]

Код

В отличие от предыдущих частей, где получалось обходиться одним keras’ом, здесь с этим возникает проблема. А именно, нужно в одной и той же сети по очереди обновлять либо только параметры генератора, либо только дискриминатора. Если исхитриться, то можно сделать это и чисто в keras’е, но по мне проще и полезнее подключить сюда и tensorflow.
В блоге keras’а есть небольшой туториал [3], как это делать.

Благо keras легко сочетается с tensorflow — не даром он попал в tensorflow.contrib.

Начнем с импортирования нужных модулей и загрузки датасета.

from IPython.display import clear_output
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

from keras.layers import Dropout, BatchNormalization, Reshape, Flatten, RepeatVector
from keras.layers import Lambda, Dense, Input, Conv2D, MaxPool2D, UpSampling2D, concatenate
from keras.layers.advanced_activations import LeakyReLU
from keras.models import Model, load_model


from keras.datasets import mnist
from keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test  = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test  = np.reshape(x_test,  (len(x_test),  28, 28, 1))

y_train_cat = to_categorical(y_train).astype(np.float32)
y_test_cat  = to_categorical(y_test).astype(np.float32)

Для работы в keras и tensorflow одновременно надо зарегистрировать tensorflow сессию в keras, это нужно для того чтобы keras создавал все внутренние переменные в рамках используемой сессии.

from keras import backend as K
import tensorflow as tf
sess = tf.Session()
K.set_session(sess)

Определим основные глобальные константы:

batch_size = 256
batch_shape = (batch_size, 28, 28, 1)
latent_dim = 2
num_classes = 10
dropout_rate = 0.3

Обучать модель мы теперь будем не с помощью метода .fit, а напрямую из tensorflow, поэтому напишем итератор, возвращающий очередной батч:

def gen_batch(x, y):
    n_batches = x.shape[0] // batch_size
    while(True):
        for i in range(n_batches):
            yield x[batch_size*i: batch_size*(i+1)], y[batch_size*i: batch_size*(i+1)]
        idxs = np.random.permutation(y.shape[0])
        x = x[idxs]
        y = y[idxs]


train_batches_it = gen_batch(x_train, y_train_cat)
test_batches_it  = gen_batch(x_test,  y_test_cat)

Оборачиваем placeholder’ы для картинок, лейблов и скрытых переменных во входящие слои для keras моделей:

x_ = tf.placeholder(tf.float32, shape=(None, 28, 28, 1),   name='image')
y_ = tf.placeholder(tf.float32, shape=(None, num_classes), name='labels')
z_ = tf.placeholder(tf.float32, shape=(None, latent_dim),  name='z')

img = Input(tensor=x_)
lbl = Input(tensor=y_)
z   = Input(tensor=z_)

Реализовывать будем сразу CGAN, так как он лишь минимально отличается от обычного.
Напишем модель генератора. Keras работает со scope’ами, а нам нужно разделить генератор и дискриминатор, чтобы потом обучать их по-отдельности

with tf.variable_scope('generator'):
    x = concatenate([z, lbl])
    x = Dense(7*7*64, activation='relu')(x)
    x = Dropout(dropout_rate)(x)
    x = Reshape((7, 7, 64))(x)
    x = UpSampling2D(size=(2, 2))(x)

    x = Conv2D(64, kernel_size=(5, 5), activation='relu', padding='same')(x)
    x = Dropout(dropout_rate)(x)

    x = Conv2D(32, kernel_size=(3, 3), activation='relu', padding='same')(x)
    x = Dropout(dropout_rate)(x)
    x = UpSampling2D(size=(2, 2))(x)

    generated = Conv2D(1, kernel_size=(5, 5), activation='sigmoid', padding='same')(x)
generator = Model([z, lbl], generated, name='generator')

Далее модель дискриминатора. Здесь нам нужно добавить ко входящему изображению еще лейбл цифры. Для этого после применения первого сверточного слоя добавим к фильтрам лейблы. Сперва функция, которая это делает, потом модель дискриминатора.

def add_units_to_conv2d(conv2, units):
    dim1 = int(conv2.shape[1])
    dim2 = int(conv2.shape[2])
    dimc = int(units.shape[1])
    repeat_n = dim1*dim2
    units_repeat = RepeatVector(repeat_n)(lbl)
    units_repeat = Reshape((dim1, dim2, dimc))(units_repeat)
    return concatenate([conv2, units_repeat])


with tf.variable_scope('discrim'):
    x = Conv2D(128, kernel_size=(7, 7), strides=(2, 2), padding='same')(img)
    x = add_units_to_conv2d(x, lbl)
    x = LeakyReLU()(x)
    x = Dropout(dropout_rate)(x)
    x = MaxPool2D((2, 2), padding='same')(x)
    
    l = Conv2D(128, kernel_size=(3, 3), padding='same')(x)
    x = LeakyReLU()(l)
    x = Dropout(dropout_rate)(x)

    h = Flatten()(x)
    d = Dense(1, activation='sigmoid')(h)
discrim = Model([img, lbl], d, name='Discriminator')

Определив модели, мы можем применять их напрямую к placeholder’ам как обычные tensorflow операции.


generated_z = generator([z, lbl])

discr_img   = discrim([img, lbl])
discr_gen_z = discrim([generated_z, lbl])

gan_model = Model([z, lbl], discr_gen_z, name='GAN')
gan   = gan_model([z, lbl])

Теперь лосс ошибки определения реального изображения, и лосс сгенерированного, а также на их основе лоссы генератора и дискриминатора.

log_dis_img   = tf.reduce_mean(-tf.log(discr_img + 1e-10))
log_dis_gen_z = tf.reduce_mean(-tf.log(1. - discr_gen_z + 1e-10))

L_gen = -log_dis_gen_z
L_dis = 0.5*(log_dis_gen_z + log_dis_img)

Обычно в tensorflow, передавая в оптимизатор лосс, он будет пытаться минимизировать сразу все переменные, от которых он зависит. Нам сейчас этого не надо: при обучении генератора, ошибка не должна трогать дискриминатор, хотя должна сквозь него течь и наоборот.

Для этого дополнительно в оптимизатор надо передать список переменных, которые он будет оптимизировать. Достанем эти переменные из нужных scope’ов с помощью tf.get_collection

optimizer_gen = tf.train.RMSPropOptimizer(0.0003)
optimizer_dis = tf.train.RMSPropOptimizer(0.0001)

# Переменные генератора и дискриминаторы (отдельно) для оптимизаторов
generator_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, "generator")
discrim_vars   = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, "discrim")

step_gen = optimizer_gen.minimize(L_gen, var_list=generator_vars)
step_dis = optimizer_dis.minimize(L_dis, var_list=discrim_vars)

Инициализируем переменные:

sess.run(tf.global_variables_initializer())

Отдельно напишем функции, которые будем вызывать для обучения генератора и дискриминатора:

# Шаг обучения генератора
def step(image, label, zp):
    l_dis, _ = sess.run([L_dis, step_gen], feed_dict={z:zp, lbl:label, img:image, K.learning_phase():1})
    return l_dis

# Шаг обучения дискриминатора
def step_d(image, label, zp):
    l_dis, _ = sess.run([L_dis, step_dis], feed_dict={z:zp, lbl:label, img:image, K.learning_phase():1})
    return l_dis

Код сохранения и визуализации картинок:

Код


# Массивы, в которые будем сохранять результаты, для последующей визуализации
figs = [[] for x in range(num_classes)]
periods = []

save_periods = list(range(100)) + list(range(100, 1000, 10))

n = 15 # Картинка с 15x15 цифр
from scipy.stats import norm
# Так как сэмплируем из N(0, I), то сетку узлов, в которых генерируем цифры, берем из обратной функции распределения
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
def draw_manifold(label, show=True):
    # Рисование цифр из многообразия
    figure = np.zeros((28 * n, 28 * n))
    input_lbl = np.zeros((1, 10))
    input_lbl[0, label] = 1.
    for i, yi in enumerate(grid_x):
        for j, xi in enumerate(grid_y):
            z_sample = np.zeros((1, latent_dim))
            z_sample[:, :2] = np.array([[xi, yi]])

            x_generated = sess.run(generated_z, feed_dict={z:z_sample, lbl:input_lbl, K.learning_phase():0})
            digit = x_generated[0].squeeze()
            figure[i * 28: (i + 1) * 28,
                   j * 28: (j + 1) * 28] = digit
    if show:
        # Визуализация
        plt.figure(figsize=(10, 10))
        plt.imshow(figure, cmap='Greys')
        plt.grid(False)
        ax = plt.gca()
        ax.get_xaxis().set_visible(False)
        ax.get_yaxis().set_visible(False)
        plt.show()
    return figure


n_compare = 10
def on_n_period(period):
    clear_output() # Не захламляем output

    # Рисование многообразия для рандомного y
    draw_lbl = np.random.randint(0, num_classes)    
    print(draw_lbl)
    for label in range(num_classes):
        figs[label].append(draw_manifold(label, show=label==draw_lbl))

    periods.append(period)

Обучим теперь наш CGAN.

Важно, чтобы в самом начале дискриминатор не слишком стал побеждать, иначе обучение остановится. Поэтому здесь добавлены внутренние циклы как для дискриминатора, так и для генератора, и выход из них, когда одна сеть почти догоняет другую.

Если дискриминатор сразу выигрывает у декодера, и обучение даже не успевает начаться, то можно попробовать замедлить обучение дискриминатора, либо несколько раз начинать заново.


batches_per_period = 20 # Как часто сохранять картинки
k_step = 5 # Количество шагов, которые могут делать дискриминатор и генератор во внутреннем цикле

for i in range(5000):
    print('.', end='')
    # Достанем новый батч
    b0, b1 = next(train_batches_it)
    zp = np.random.randn(batch_size, latent_dim)
    # Шаги обучения дискриминатора
    for j in range(k_step):
        l_d = step_d(b0, b1, zp)
        b0, b1 = next(train_batches_it)
        zp = np.random.randn(batch_size, latent_dim)
        if l_d < 1.0:
            break

    # Шаги обучения генератора
    for j in range(k_step):
        l_d = step(b0, b1, zp)
        if l_d > 0.4:
            break
        b0, b1 = next(train_batches_it)
        zp = np.random.randn(batch_size, latent_dim)

    # Периодическое рисование результата
    if not i % batches_per_period:
        period = i // batches_per_period
        if period in save_periods:
            on_n_period(period)
        print(l_d)

Код рисования гифок:

Код


from matplotlib.animation import FuncAnimation
from matplotlib import cm
import matplotlib

def make_2d_figs_gif(figs, periods, c, fname, fig, batches_per_period): 
    norm = matplotlib.colors.Normalize(vmin=0, vmax=1, clip=False)
    im = plt.imshow(np.zeros((28,28)), cmap='Greys', norm=norm)
    plt.grid(None)
    plt.title("Label: {}\nBatch: {}".format(c, 0))

    def update(i):
        im.set_array(figs[i])
        im.axes.set_title("Label: {}\nBatch: {}".format(c, periods[i]*batches_per_period))
        im.axes.get_xaxis().set_visible(False)
        im.axes.get_yaxis().set_visible(False)
        return im
    
    anim = FuncAnimation(fig, update, frames=range(len(figs)), interval=100)
    anim.save(fname, dpi=80, writer='imagemagick')

for label in range(num_classes):
    make_2d_figs_gif(figs[label], periods, label, "./figs4_5/manifold_{}.gif".format(label), plt.figure(figsize=(10,10)), batches_per_period)

Результаты:

GAN

Многообразие цифр для обычного GAN (без передачи лейблов)

Стоит отметить, что цифры получаются лучше, чем в VAE (без лейблов)

Гифка обучения

CGAN

Многообразия цифр для каждого лейбла

Тяжелые гифки

Полезные ссылки и литература

Оригинальная статья:
[1] Generative Adversarial Nets, Goodfellow et al, 2014, https://arxiv.org/abs/1406.2661

Conditional GANs:
[2] Conditional Generative Adversarial Nets, Mirza, Osindero, 2014, https://arxiv.org/abs/1411.1784

Туториал про использование keras вместе с tensorflow:
[3] https://blog.keras.io/keras-as-a-simplified-interface-to-tensorflow-tutorial.html