PatientZero Oct 20 2017 at 11:04

Структура и случайность простых чисел

22 min

39K

Translation

Разбросаны ли простые числа по числовой оси подобно рассеянным ветром семенам? Разумеется нет: простота — это не вопрос случайности, а результат элементарной арифметики. Число является простым тогда и только тогда, когда ни одно меньшее положительное целое число кроме единицы не делит его нацело.

Но на этом история не заканчивается. Распределение простых чисел выглядит случайным, с неравномерными разрывами и скоплениями, которые выглядят довольно хаотично. Если и существует какая-то схема, то она непостижима. На самом деле, простые числа выглядят достаточно случайными, чтобы можно было сыграть с ними в кости. Создайте список последовательных простых чисел (допустим, начав с 11, 13, 17, 19,... ) и разделите их по модулю 7. Другими словами, разделите каждое простое число на 7 и сохраните только остаток. Результатом будет последовательность целых чисел из множества {1, 2, 3, 4, 5, 6}, которая выглядит почти как результат нескольких бросков правильной кости.

$\begin{align*} 11 \bmod 7 & \rightarrow 4 \qquad 47 \bmod 7 \rightarrow 5 \\ 13 \bmod 7 & \rightarrow 6 \qquad 53 \bmod 7 \rightarrow 4 \\ 17 \bmod 7 & \rightarrow 3 \qquad 59 \bmod 7 \rightarrow 3 \\ 19 \bmod 7 & \rightarrow 5 \qquad 61 \bmod 7 \rightarrow 5 \\ 23 \bmod 7 & \rightarrow 2 \qquad 67 \bmod 7 \rightarrow 4 \\ 29 \bmod 7 & \rightarrow 1 \qquad 71 \bmod 7 \rightarrow 1 \\ 31 \bmod 7 & \rightarrow 3 \qquad 73 \bmod 7 \rightarrow 3 \\ 37 \bmod 7 & \rightarrow 2 \qquad 79 \bmod 7 \rightarrow 2 \\ 41 \bmod 7 & \rightarrow 6 \qquad 83 \bmod 7 \rightarrow 6 \\ 43 \bmod 7 & \rightarrow 1 \qquad 89 \bmod 7 \rightarrow 5 \\ \end{align*}$

Поработав с большей выборкой (первым миллионом простых чисел больше $inline$ ), я подсчитал количество простых чисел с каждым из шести возможных остатков по модулю 7 (также известных как шесть возможных классов конгруэнции по модулю 7). Также я симулировал миллион бросков шестигранной кости. Сможете ли вы сказать, глядя на эти два результата, что из них что?

               1        2        3        4        5        6
         166 787  166 569  166 714  166 573  166 665  166 692
             120      -98       47      -94       -2       25

               1        2        3        4        5        6
         166 768  166 290  166 412  166 638  167 282  166 610
             101     -377     -255      -29      615      -57

В каждой таблице первая строка означает количество результатов $inline$ в каждом из шести классов. Во второй строке показана разность $x - \bar{x}$ , где $\bar{x}$ — среднее значение $inline$ . В обоих случаях кажется, что числа распределены довольно равномерно, без очевидных смещений. В первой таблице представлены остатки простых чисел от деления по модулю 7. Их распределение немного более плоское по сравнению с симулированной костью и с меньшими отклонениями от среднего; стандартное отклонение двух выборок равно соответственно 84 и 346. Судя по этим таблицам, похоже, что любой из процессов можно использовать для обеспечения случайности, необходимой в обычной игре в кости.

Но условием случайности является не только равномерное распределение результатов в допустимом интервале. Кроме того, отдельные события в последовательности должны быть независимы друг от друга. Один бросок кости не должен влиять на результат следующего броска. Для проверки независимости можно взглянуть на последовательные события. Сколько раз за единицей идёт ещё одна единица, или двойка, или тройка, и так далее? Запишем в матрицу $inline$ количество всех 36 возможных пар. Если процесс действительно случаен, все 36 пар должны иметь одинаковую частотность, если не принимать во внимание небольшие статистические флуктуации. Можно превратить матрицу в цветную «тепловую карту», в которой ячейки с количеством выше среднего будут отображены в тёплых оттенках розового и красного, а ниже среднего — залиты более холодными оттенками синего. (Вносимые количества являются не действительным количеством $inline$ , а нормализованной переменной $w = (x_{i,\,j} - \bar{x}, /\, \bar{x}$ , где $\bar{x}$ — это снова среднее значение, в нашем случае $inline$ .) Вот тепловая карта симулированной правильной кости:

Рисунок 1.

Здесь нет ничего интересного. Почти все количества настолько близки к среднему значению, что ячейки матрицы кажутся нейтрально серыми, только немногие оказались бледно-розовыми или голубыми. Именно такого результата и ждёшь, когда последовательные броски кости не коррелируют друг с другом, и все возможные пары одинаково вероятны.

Теперь перейдём к соответствующей матрице последовательных простых чисел по модулю 7:

Рисунок 2.

Ого! Похоже мы покинули Страну случайных чисел, здесь старое серое кино превратилось в Technicolor. На тепловой карте появилась голубая полоса вдоль основной диагонали (из левого верха в правый низ), означающая, что последовательные пары простых чисел, имеющие одинаковое значение остатка от деления на 7, очень маловероятны. Другими словами, пары $(1, 1), (2, 2), \ldots (6, 6)$ возникают реже, чем это было бы в действительно случайной последовательности. Наддиагональ (прямо над основной диагональю) имеет более светлый голубой цвет. Это означает, что пары $inline$ , где $inline$ , возникают немного реже, чем средняя частота. Например, $inline$ и $inline$ имеют немного отрицательные значения нормализованной частоты. С другой стороны, поддиагональ (под основной диагональю) полностью розовая и красная; такие пары как $inline$ или $inline$ , где $inline$ , возникают с частотой выше средней. Вдали от диагонали, в верхнем правом и нижнем левом углу мы видим пастельный шахматный узор.

Если вы предпочитаете иметь дело с числами, а не с цветными квадратами, то вот вам матрица значений:

           пары последовательных простых чисел mod 7
                   1      2      3      4      5      6
          1    15656  24376  33891  29964  33984  28916
          2    37360  15506  22004  32645  25095  33959
          3    25307  41107  14823  22747  32721  30009
          4    32936  26183  37129  14681  21852  33791
          5    24984  34207  26231  41154  15560  24529
          6    30543  25190  32636  25382  37453  15488

Отклонения от единообразия можно назвать какими угодно, но не «незначительными». В третьем ряду, например, видно, что если вы только что встретили 3 в последовательности простых чисел mod 7, то следующее число с намного большей вероятностью будет 2, а не ещё одна 3. Если бы вы играли в игру с костями из простых чисел, то такое смещение колоссально повлияло бы на результат. Кости на простых числах — «заряженные» кости!

Эти примечательно сильные корреляции в парах были открыты Робертом Дж. Лемке-Оливером и Каннаном Соундарараджаном из Стэнфордского университета. Они обсуждали их в препринте, опубликованном на arXiv в марте этого года. Для меня самым удивительным в этом открытии стало то, что никто за долгие годы не заметил эти структуры. Они довольно очевидны, если знать, где из искать.

Думаю, нельзя винить Евклида, за то что он их не нашёл: в античности не были развиты идеи случайности и вероятности. Но как насчёт Гаусса? Он был знатоком таблиц простых чисел, и создал собственные списки тысяч простых чисел. В юности он писал: «одним из моих первых проектов стало наблюдение за уменьшающейся частотой простых чисел, для чего я высчитал несколько тысяч простых чисел...» Более того, Гаусс практически изобрёл идею классов конгруэнции и модульной арифметики. Но очевидно, он никогда не подозревал, что в конгруэнциях пар последовательных простых чисел может таиться что-то странное.

В 1850-х российский математик Пафнутий Львович Чебышев указал на незначительное искажение в простых числах. Деление нечётных простых чисел по модулю 4 разбивает их на два подмножества. Все простые числа в ряду 5, 13, 17, 29, 37,... конгруэнтны 1 по модулю 4; в ряду 3, 7, 11, 19, 23, 31,... конгруэнтны 3 по модулю 4. Чебышев заметил, что простые числа во второй категории кажутся более многочисленными. Например, среди первых 10 000 нечётных простых чисел есть 4 943 конгруэнтных 1 и 5 057 конгруэнтных 3. Однако это воздействие мало по сравнению с неравномерностями, замеченными в парах последовательных простых чисел.

В наше время несколько авторов увидели намёк на феномен последовательных простых чисел. Лемке-Оливер и Соундарараджан упоминают о трёх таких свидетельствах. (См. список справочных материалов в конце статьи.) В 1950-х и 60-х Станислав Кнаповски и Пал Туран исследовали различные аспекты остатков от деления простых чисел по модулю m. В одной статье, посмертно опубликованной 1977 году, они рассматривали деление последовательных простых чисел по модулю 4 с остатками 1 или 3. Они «предположили», что последовательные пары с одинаковым остатком и пары с отличающимися остатками «не равновероятны». В 2002 году Чун-Мин Ко исследовал ряды последовательных простых чисел (не только их пар) и создал проработанные фрактальные паттерны на основе их меняющихся частот. Затем в 2011 году Авнер Эш с коллегами опубликовал подробный анализ «Частоты последовательных пар остатков простых чисел», в том числе несколько матриц, в которых диагональное снижение чётко заметно.

С учётом этих прецедентов были ли Лемке-Оливер и Соундарараджан на самом деле открывателями корреляций последовательных простых чисел? По моему мнению, ответ должен быть положительным. Хотя другие и видели эти паттерны ранее, они не описывали их так, чтобы те зафиксировались в сознании математического сообщества. На самом деле, когда Лемке-Оливер и Соундарараджан объявили о своих находках, реакцией стало удивление, граничащее с недоверием. Эрика Кларарайх в статье для Quanta процитировала реакцию оксфордского теоретика чисел Джеймса Мэйнарда:

Когда Соундарараджан впервые сказал Мэйнарду об открытии пары, Мэйнард сказал «Я поверил ему только наполовину. Как только я вернулся к себе в офис, я провёл численный эксперимент, чтобы убедиться в этом самому».

Очевидно, что такой была всеобщая реакция. Эвелин Лэмб в статье для Nature цитирует Соундарараджана: «Каждый, кому мы рассказывали об этом, в конце концов писал свою компьютерную программу, чтобы убедиться в этом самому».

Так же поступил и я! За последние несколько недель я написал кучу строк кода для анализа деления простых чисел по модулю m. Моя статья — это отчёт о моим попытках разобраться в том, откуда взялись эти паттерны. Мои методы больше вычислительные и визуальные, чем математические, я не могу ничего доказать. Лемке-Оливер и Соундарараджан применили более строгий и аналитический подход, в конце этой статьи я расскажу немного больше об их результатах.

Если вы хотите начать собственное расследование, то можете взять за основу мой код. Он написан на языке программирования Julia, упакован в Jupyter notebook и доступен на GitHub. (Так получилось, что эта программа стала моим первым нетривиальным экспериментом с Julia. В другой статье я расскажу подробнее о моей работе с языком.)

Во всех представленных выше примерах приведено деление простых чисел по модулю 7, но в числе 7 нет ничего особенного. Я выбрал его просто потому, что шесть возможных остатков {1, 2, 3, 4, 5, 6} соответствуют граням обычной кубической кости. Другие модули дают схожие результаты. Лемке-Оливер и Соундарараджан бо́льшую часть анализа провели над делением простых чисел по модулю 3, при котором есть только два класса конгруэнции: простое число больше 3 должно при делении на 3 иметь остаток 1 или 2. Вот матрица количеств пар для первого миллиона простых чисел больше $inline$ :

                             1       2
                    1   218578  281453
                    2   281454  218514

Рисунок 3.

Паттерн довольно минималистичен, но всё равно узнаваем: элементы вне диагонали для последовательностей $inline$ и $inline$ больше, чем элементы на диагонали для $inline$ и $inline$ .

Простые числа по модулю 10 имеют четыре класса конгруэнции: 1, 3, 7, 9. Чтобы увидеть это, работая в десятичной нотации, нам даже не нужна арифметика. Когда числа записываются по основанию 10, каждое простое число больше 5 имеет конечную цифру 1, 3, 7 или 9. Вот частоты для 16 пар последовательных конечных цифр:

                          1      3      7      9
                 1    43811  76342  78170  51644
                 3    58922  41148  71824  78049
                 7    64070  68542  40971  76444
                 9    83164  63911  59063  43924

Рисунок 4.

Чётко видна голубая полоса по основной диагонали, хотя в других местах матрицы паттерн немного ослаблен и смазан.

Я обнаружил, что корреляции между последовательными простыми числами проявляются наиболее чётко, когда сам модуль является простым числом, и при этом не слишком маленьким. Посмотрите на тепловые карты для последовательных простых чисел mod 13 и mod 17:

Рисунок 5.

Рисунок 6.

А как насчёт модуля 31?

Рисунок 7.

Из этих матриц получится отличный узор для килта или мозаичного пола, правда? И во всех них видны интересные закономерности. Диагональные полосы выделяются не только на основной диагонали, но и во всей матрице. Такие полосы также создают узор шахматной доски. Вдоль любой строки или столбца ячейки обычно попеременно красные и синие. Более незаметной особенностью является приблизительная двухсторонняя симметрия вдоль противоположной диагонали (идущей из левого низа в правый верх). Если сложить по этой линии квадрат, то соединённые вместе ячейки будут примерно одного цвета. (Этот факт заметил Эш и его соавторы.)

Для дальнейшего анализа я решил сосредоточиться на последовательных простых числах mod 19. Модуль достаточно велик, чтобы давать в результате чётко дифференцированные полосы, но не настолько велик, чтобы сделать матрицу огромной.

Рисунок 8.

Как понять смысл того, что мы видим? Мы начнём наблюдения с того, что все простые числа в нашей выборке являются нечётными, а потому все интервалы между этими простыми являются чётными числами. Для любого заданного простого $inline$ следующими кандидатами на звание простого числа становятся $p+2, p+4, p+6, \ldots$ . Связано ли это как-то с рисунком шахматной доски? Если шаги между простыми числами должны быть кратными 2, это определённо может создать корреляции между каждой второй ячейкой любого столбца или строки. (И в самом деле, корреляции с ячейкой через раз должны быть чётко заметны — все чётные элементы должны равняться нулю, если модуль был бы чётным числом. Чётные ячейки можно заполнить только «циклическим возвратом» края матрицы к нечётной границе.)

Диагональные полосы в матрице предполагают наличие сильной корреляции между всеми парами, разделёнными определённым числовым интервалом. Например, самая тёмно-синяя диагональ и самая ярко-красная диагональ состоят из ячеек, разделённых шестью элементами вдоль оси j. В первой строке находятся ячейки 1 и 7, потом 2 и 8, 3 и 9, и так далее. Мне показалось, что эту взаимосвязь проще воспринимать, если «изогнуть» матрицу, чтобы диагонали стали столбцами. Идея заключается в том, чтобы применить к каждой строке циклический сдвиг, все значения в строке сместятся влево, а те, которые «упадут» с левого края, будут вставлены справа. Первая строка смещается на ноль позиций, следующая — на одну позицию, и так далее. (Есть ли название для такого преобразования? Я просто буду называть его «изгиб».)

Затем я написал код для этого преобразования, но в результате получил не совсем то, что ожидал:

Twisted nz heatmap 8 digit primes 1000001 mod 19

Рисунок 9.

Что это за зигзаги вдоль обратной диагонали? Я предположил, что совершил ошибку и сместил на один лишний элемент. И корень проблемы действительно оказался в этом, но «баг» находится не в алгоритме, а в самих данных. Матрицы, показанные мной во всех предыдущих рисунках, являются только частичными, они отбрасывают пустые классы конгруэнции. В частности, матрица для пар простых чисел по модулю 19 игнорирует все простые числа, конгруэнтные 0 по модулю 19 на том логичном основании, что таких простых чисел нет. В конце концов, если $inline$ и $p \equiv 0 \bmod 19$ , то $inline$ не может быть простым, потому что оно делится на 19. Тем не менее, строка и столбец для $p \equiv 0 \bmod 19$ являются действительной частью матрицы. Если их добавить, то наше табло с цветовой кодировкой будет выглядеть так:

Рисунок 10.

Присутствие нулевой строки и столбца делает определение преобразования изгибом более аккуратным: для каждой строки $inline$ применяем циклический сдвиг влево на $inline$ мест. Получившаяся изогнутая матрица тоже выглядит опрятнее:

Twisted z heatmap 8 digit primes 1000001 mod 19

Рисунок 11.

О чём нам говорят эти вертикальные полосы? В исходной матрице элемент $inline$ представлял собой частоту, с которой за $i \bmod 19$ следует $j \bmod 19$ . Здесь цвет ячейки $inline$ обозначает частоту, с которой за $i \bmod 19$ следует $(i + j) \bmod 19$ . Другими словами, каждый столбец объединяет элементы с одинаковым интервалом mod 19 между двумя простыми числами. Например, самый левый столбец содержит все пары, разделённые интервалом длиной $0 \bmod 19$ , а ярко-красный столбец в $inline$ учитывает все случаи, когда последовательные простые числа отделены друг от друга $6 \bmod 19$ .

Цветовое кодирования даёт нам качественное представление о том, какие интервалы появляются более или менее часто. Для более точного количественного измерения мы можем суммировать вдоль столбцов и отобразить результаты в столбчатом графике:

Column sums twisted 8 digit primes 1000001 mod 19

Рисунок 12.

Три наблюдения:

Замеченная выше неравномерность чётных-нечётных чисел явно заметна и на графике. За исключением 0, каждый чётный интервал выделяется на фоне его нечётных соседей.
Интервал между простыми числами mod 19, равный 6 — самый популярный из всех. Числа, кратные 6 (а именно 12 и 18) тоже часты, но хоть и в меньшей степени.
Интервал между простыми числами mod 19, равный 0, примечательно непопулярен. Это элементы вдоль основной диагонали исходной матрицы, поэтому неудивительно, что их сумма находится на нижней части, однако дефицит сильнее, чем я предполагал.

Я хотел разобраться с источниками этих паттернов. Что делает интервал 6 таким притягательным для пар последовательных простых чисел, и почему почти все простые числа сторонятся бедного интервала 0?

У меня уже есть отдалённая догадка относительно популярности 6. В 1990-х Эндрю Одлыжко, Майкл Рубинштейн и Марек Вулф выполнили вычислительное исследование «чемпионов по прыжкам» среди простых чисел:

Целое число D называется чемпионом по прыжкам, если его наиболее часто возникающая разность между последовательными простыми числами ≤ x для некоторого x.

Среди наименьших простых чисел (x меньше, чем примерно 600), чемпионом по прыжкам обычно является 2, но потом выигрывает 6 и доминирует на довольно большом интервале числовой оси. Примерно возле $x = 10^{35}$ число 6 уступает чемпионство числу 30, которое со временем уступает 210. Одлыжко с коллегами оценили, что этот последний переход происходит примерно около $x = 10^{425}$ . Числа в этой последовательности чемпионов по прыжкам — 2, 6, 30, 210,… — являются праймориалами; n-ный праймориал является произведением первых n простых чисел.

Почему праймориалы становятся предпочтительными интервалами между последовательными простыми числами? Если $inline$ является достаточно большим простым числом, то $inline$ не может делиться на 2, $inline$ не может делиться на 2 и 3, $inline$ не может делиться на 2, 3 и 5, и в целом $p + P_{n}$ , где $P_{n}$ — это n-ный праймориал, не делится ни на один из первых n простых чисел. Разумеется $p + P_{n}$ всё равно может делиться на какое-то большое простое число, или может существовать другое простое число между $inline$ и $p + P_{n}$ , такое, что интервал между простыми числами не гарантированно является праймориалом. Но эти интервалы имеют преимущество перед остальными претендентами.

Мы можем увидеть это обоснование в действии, взяв разность между последовательными элементами нашего списка из миллиона восьмиразрядных простых чисел и нанеся на график их частоты:

Рисунок 13.

Снова явно выделяется интервал 6, насчитывающий 13,7% от общего количества, бо́льшие кратные числа 6 тоже выделяются среди своих непосредственных соседей. Стоит заметить и общую форму распределения: скопление слева (с пиком на числе 6) с последующим плавным снижением. Тренд похож на распределение Пуассона, и на самом деле это можно считать верным описанием.

Цветовая схема разрезает множество данных на доли по 19 значений в каждой. Голубая доля, в которую входят интервалы между простыми числами длиной от 0 до 18, насчитывает 68 процентов от всех интервалов, присутствующих в выборке из миллиона простых чисел; золотая доля добавляет ещё 23 процента. Остальные 9 процентов распределены широко и равномерно. На графике показаны не все интервалы: спектр продолжается до 210. (Одна пара последовательных простых чисел в выборке имеет расстояние 210, а именно 20 831 323 и 20 831 533.)

Похоже, на Рисунке 13 показана бо́льшая часть паттерна последовательных простых чисел по модулю19. Я могу сделать график ещё более информативным, внеся простое изменение. Начнём сдвигать каждую долю из 19-элементов, пока она не выровняется с долей 0, собираясь в столбики, находящиеся в одном столбце. Поскольку вторая (золотая) доля перемещается влево, пока столбик 19 не выровняется с столбцом 0, а третья (розовая) доля соединяет столбик 38 со столбиком 0. Физически этот процесс можно представить как вращение графика вокруг цилиндра с длиной окружности 19. Математически он составляет деление интервалов между простыми числами по модулю 19.

Diffs 8 digit primes 1000001 color stacked mod 19

Рисунок 14.

Если не обращать внимание на слишком яркие цвета, Рисунок 14 аналогичен Рисунку 12: высоты всех столбиков совпадают. Это не должно нас удивлять. На Рисунке 12 мы делим простые числа по модулю 19, а затем берём разности между последовательными разделёнными простыми числами. На Рисунке 14 мы берём разности между самими простыми числами, а затем делим эти разности по модулю 19. Две процедуры аналогичны:

$(p \bmod 19 - q \bmod 19) \bmod 19 = (p - q) \bmod 19.$

Изучив цвета, мы можем расставить все фрагменты головоломки на места. Почему простые числа mod 19 так часто разделены интервалом 6? Ну, на самом деле mod 19 имеет с этим мало общего; само число 6 в этой выборке является наиболее частым интервалом между простыми числами. Единственный другой существенный взнос в $\delta \equiv 6 \bmod 19$ возникает из третьей доли, особенно несколько пар простых чисел с расстоянием в 44.

Превосходство первой доли также объясняет неравенство между чётными и нечётными интервалами. Все интервалы в первой доле обязательно чётные, нечётные интервалы (mod 19) начинают появляться только во второй доле (интервалы от 19 до 37) и только по этой причине они менее часты. Для восьмиразрядных простых чисел выборки больше двух третей последовательных пар ближе, чем на 19 единиц, и поэтому оказываются в первой доле. (Медианное расстояние между простыми числами равно 12. Средний интервал равен 16,68, что близко к теоретическому предсказанию в 16,72.)

Наконец, Рисунок 14 может кое-что нам рассказать и о редкости интервалов 0 mod 19. Никакие два последовательных простых числа не могут попасть в один класс конгруэнции mod 19, если только они не разделены расстоянием 38 или числом, кратным 38. Поэтому такие пары не выходят на сцену до начала третьей доли, и в ней их не может быть слишком много. Выборка из миллиона простых чисел содержит 8 384 последовательных пар с расстоянием 38 — меньше одного процента от общего числа. И это основная причина того, что кость простых чисел так редко выпадает одной и той же гранью дважды подряд. В этом заключается причина появления голубой диагональной полосы во всех матрицах.

Я нахожу очень интересным то, что мы можем объяснить так много о паттерне последовательных простых чисел mod m, не углубляясь в подробности и не рассматривая особые свойства простых чисел. На самом деле мы можем воссоздать значительную часть паттерна вообще без использования простых чисел.

Две сотни лет назад Гаусс и Лежандр заметили, что по соседству с числом $inline$ доля всех целых чисел, являющихся простыми, составляет примерно $1 / \log x$ . В 1936 году шведский математик Харальд Крамер предпожил интерпретировать эту долю как вероятность. Идея заключалась в том, чтобы пройти по всем целым числам по порядку, приняв каждое $inline$ с вероятностью $1 / \log x$ . Числа в принятом множестве не будут являться простыми, кроме как по совпадению, но они будут иметь то же крупномасштабное распределение, что и распределение простых чисел. Вот несколько первых элементов списка миллиона таких «простых чисел Крамера», где процесс случайного выбора начинается с $inline$ :

Теперь предположим, что мы пропустим эти числа через тот же механизм, который применяли к простым числам. Мы поделим каждое простое число Крамера по модулю 19, а затем создадим матрицу последующих чисел $inline$ :

Рисунок 15.

Выделяющиеся диагональные особенности выглядят похожими, но они гораздо проще, чем в соответствующих графиках простых чисел. Для любого простого числа Крамера p mod 19, наиболее вероятным последователем будет p + 1 mod 19, а наименее вероятным — p + 19 mod 19. Между этими предельными случаями находится плавный градиент частоты или вероятности со всего лишь несколькими небольшими флуктуациями, которые скорее всего можно списать на статистический шум.

В этой матрице отсутствует только шахматный узор. Мы можем частично восстановить его структуру, сгенерировав новое множество чисел, которое я называю «полупростыми числами Крамера». Они создаются тем же вероятностным просеиванием целых чисел, но в этот раз мы рассматриваем в качестве кандидатов только нечётные числа и изменим вероятность на $2\, / \log x$ , чтобы сохранить ту же плотность:

Heatmap 8 digit semicramers 1000001 mod 19

Рисунок 16.

Вот так лучше! При исключении из последовательности чётных чисел минимальный интервал между полупростыми числами равен 2, и это также является наиболее вероятным расположением.

Добавив ещё одно изменение, мы ещё сильнее приблизимся к имитации к матрице истинных простых чисел. Кроме исключения всех целых чисел, кратных 2, мы избавимся ещё и от кратных 3 и соответствующим образом изменим вероятность выборки. Назовём получившиеся числа «полуполупростыми числами Крамера».

Heatmap 8 digit demisemicramers 1000001 mod 19

Рисунок 17.

Заметьте, что 6 mod 19 — наиболее вероятный интервал между полуполупростыми числами Крамера, как и между истинными простыми числами, и что присутствуют те же отголоски на интервалах 12 и 18. И в самом деле, единственная очевидная разница между этой матрицей и Рисунком 10 (соответствующий график для истинных простых чисел) находится в столбце и строке для чисел, конгруэнтных 0 по модулю 19. Среди простых чисел таких чисел быть не может. Если мы устраним их и из чисел Крамера, то две матрицы становятся почти неотличимыми. Вот они обе:

Рисунок 18.

Если присмотреться, то можно найти различия — посмотрите на расширение диагонали на юго-восток от строки 1, столбца 15 — но в целом эти модифицированные числа Крамера на удивление хорошо имитируют простые числа. На обеих диаграммах даже заметна симметрия относительно обратной диагонали. И не забывайте, что эти два множества содержат в общем только 19 процентов их значений: числа Крамера включают в себя 189 794 истинных простых чисел.

Я хочу добавить к этой истории ещё один поворот сюжета. Все приведённые выше примеры основаны на простых числах (или их аналогах) из восьми десятичных цифр, или, другими словами, числами по соседству с $inline$ . Справедливы ли те же результаты для простых чисел с бо́льшими значениями? Рассмотрим таблицу, созданную из последовательных пар миллиона 40-разрядных простых чисел, взятых по модулю19. Паттерн оказывается знакомым, но более бледным:

Рисунок 19.

Перейдём к простым числам из 400 разрядов, снова поделённые по модулю 19, и получим цвета, выцветшие почти до неузнаваемости:

Рисунок 20.

Голубая полоса на основной диагонали едва различима, а остальные особенности превращаются в простые случайные пятна.

Итак, похоже, что для пар последовательных простых чисел размер имеет значение. Чтобы разобраться в причинах этого, давайте посмотрим на группу различий между последовательными простыми числами в 40-разрядной выборке:

Рисунок 21.

По сравнению с распределением интервалов для восьмиразрядных простых чисел (Рисунок 13), спектр намного шире и более плоский. В этой форме график усекается на интервале 240; длинный «хвост» на самом деле растягивается далеко вправо, а наибольший разрыв между последовательными простыми числами находится в 1 328. Также, как предсказал Одлыжко с его коллегами, наиболее частый интервал между 40-разрядными простыми числами является не 6, а 30.

Из-за более широкого распределения интервалов, первая доля не может доминировать над поведением системы так, как она это делает среди восьмиразрядных простых чисел. Когда мы начинаем расставлять одну над другой доли mod 19 (Рисунок 22 ниже), первые шесть или восемь долей вносят существенный вклад. Неравномерность чётных-нечётных по-прежнему присутствует, но амплитуда этих колебаний намного снижена. Самый левый столбец графика, представляющий интервалы, конгруэнтные 0 по модулю 19, отстаёт в росте, но не так значительно.

Diffs 40 digit primes 9166432 stacked mod 19

Рисунок 22.

Выравнивание спектра становится ещё более выраженным в выборке миллиона 400-разрядных простых чисел:

Рисунок 23.

Теперь разрывы между простыми числами растянулись до 15 080, создавая почти 800 долей mod 19 (однако показаны только 13). И здесь в массиве есть очень интригующая гребенчатая структура. В целом, столбцы на числах, кратных 6 выделяются почти в два раза по сравнению с высотой ближайших соседей, показывая сохраняющееся влияние наименьших простых делителей 2 и 3. Числа, кратные 6, которые также являются кратными 30, достигают ещё больших высот. Значения в последовательности 42, 84, 126, 168, 210,… тоже вносят большой вклад: эти числа кратны $inline$ . И заметьте, что 210, которое является кратным 6 и 30 и 42, является новым интервалом-чемпионом, снова подтверждая прогноз Одлыжко.

Несмотря на всю эту внутреннюю структуру, когда столбцы, расставленные один на другой mod 19, смесь 800 доль настолько аккуратна, что высоты почти одинаковы. Единственное, что остаётся — небольшая неравномерность чётных-нечётных.

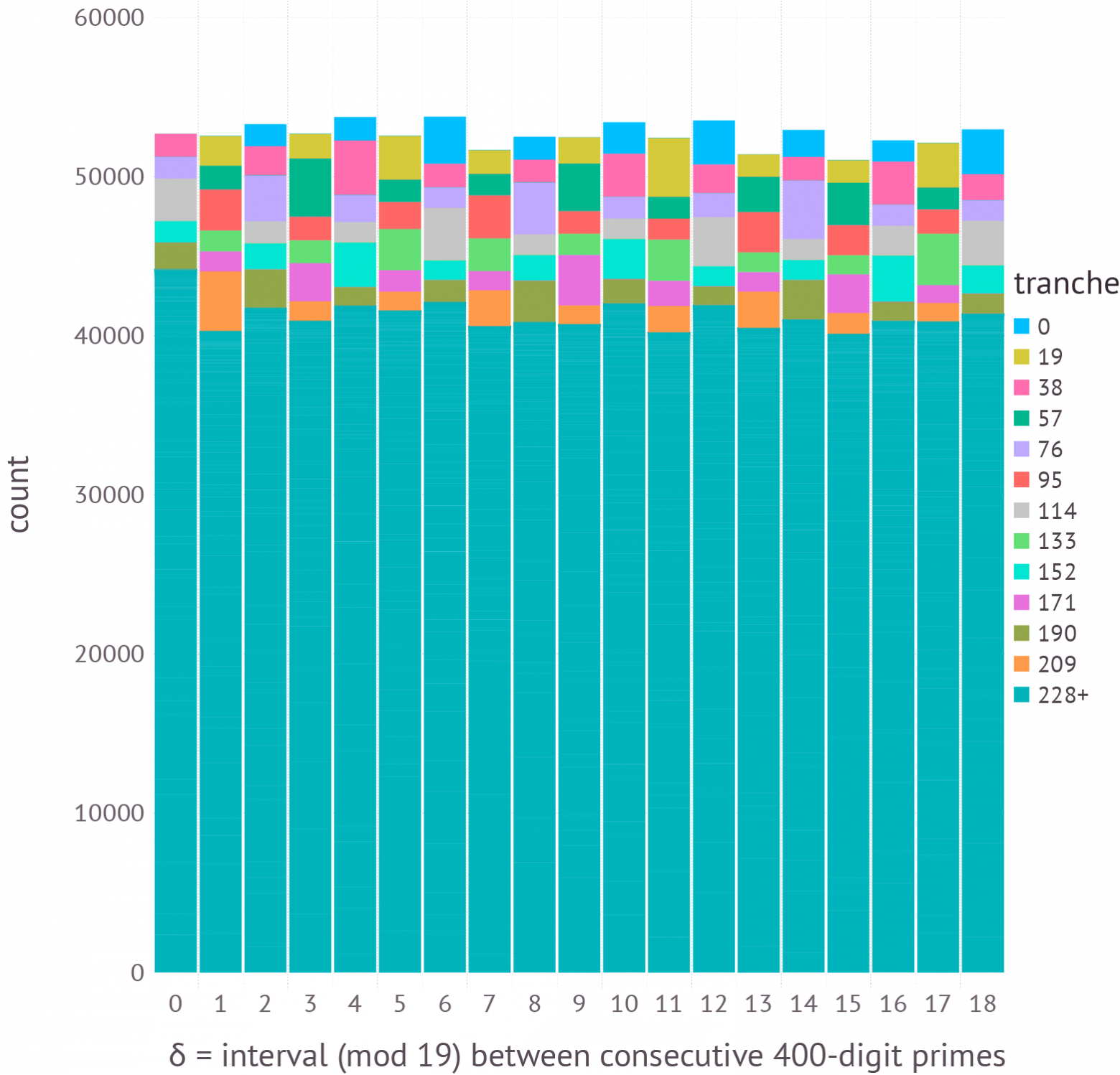
Diffs 400 digit primes 6567379 stacked mod 19

Diffs 400 digit primes 6567379 stacked mod 19

Рисунок 24.

И хронически непопулярный класс конгруэнтных 0 по модулю 19 интервалов наконец нашёл себе равных. Бо́льшая часть высоты столбца получается не от дюжины ранних доль, а от сотни более поздних, представляющих интервалы между 228 и 15 080 (все они скопились в бирюзовой области графика).

Эксперименты с большими простыми числами позволяют нам сделать правдоподобное предположение: при стремлении размера простых чисел к бесконечности все следы корреляций постепенно увядают, а последовательные пары простых чисел будут такими случайными, как броски идеальной кости. Но так ли это? Есть несколько причин относиться к этой гипотезе скептически. Во-первых, если мы будем увеличивать модуль m вместе с размером простых чисел, делая его сравнимым по величине с медианным разрывом между простыми числами, то корреляции по-прежнему будут проявляться. В моей 40-разрядной выборке медианный разрыв между простыми числами равен 66, поэтому давайте рассмотрим матрицу последовательных пар mod 61. (Чтобы ограничить статистический шум, я проведу вычисления с выборкой не из одного, а из десяти миллионов 40-разрядных простых чисел.)

Рисунок 25.

Полосы вернулись! И в самом деле, в дополнение к знакомым ярко-красным полосам на интервалах 6, есть более рассеянные розовые и голубые частоты с периодом 30. Я бы хотел посмотреть на матрицу для простых 400-разрядных чисел, у которой могут быть ещё более сложные черты, с взаимодействующими волнами в периодах 6, 30 и 210. К сожалению, я не могу показать вам этот рисунок. Медианный разрыв между 400-разрядными простыми числами равен примерно 640, так что нам придётся присвоить m значение, равное простому числу в этом интервале, скажем 641. Для заполнения матрицы $inline$ потребуется примерно миллиард последовательных 400-разрядных чисел, а это больше, чем я готов вычислять.

Существуют и другие причины сомневаться в том, что при увеличении простых чисел корреляции полностью исчезают. Гребенчатая структура, столь заметная на Рисунках 21 и 23, подсказывает нам, что правила делимости на малые простые числа сильно влияет на распределение больших простых чисел mod m, и это влияние всё равно не исчезает, когда числа увеличиваются. Более того, даже когда m намного меньше медианного интервала между простыми числами, голубая полоса остаётся слабо видимой. Вот матрица для пар последовательных 400-разрядных простых чисел mod 3:

                             1       2
                    1   248291  251128
                    2   251127  249453

Разность элементов на диагоналях и вне диагоналей намного меньше, чем с восьмиразрядными простыми числами (сравните с Рисунком 3), но отклонения по-прежнему не выглядят, как случайная вариация.

Чтобы получить более чёткое представление о том, как меняется корреляция как функция от размера простых чисел, я решил создать выборку простых чисел на всём интервале от одноразрядных до 400-разрядных чисел. В этом проекте я решил сделать лучше, чем Гаусс: он заносил простые числа в таблицы по хилиадам (по группам из 1 000), а я вычислял их по мириадам (группам по 10 000). Для измерения корреляций среди простых чисел mod m я вычислил среднее значение диагональных элементов матрицы и среднее элементов вне диагоналей, а затем взял соотношение вне/на диагонали. Если последовательные простые числа совершенно не коррелируют, то соотношение должно стремиться к 1.

На Рисунке 26 показан результат для 797 мириад простых чисел mod 3. Кривая выгнута вверх, имеет резкое начальное снижение, а затем гораздо более плоский сегмент. Начиная примерно с 100 разрядов есть выборки с соотношением меньше 1, означающим, что диагональ более густо заселена, чем области вне диагонали. Но даже при 400 разрядах большинство соотношений всё равно выше 1. Что мы здесь видим? Приближается ли кривая медленно к соотношению 1, или существует ограничивающее значение, немного большее 1? К сожалению, вычислительные эксперименты не позволяют дать окончательный ответ.

Рисунок 26.

Для рассмотрения этой задачи в статье Лемке-Оливера и Соунарараджана используются иные инструменты. Хотя они и используют численные исследования, их целью является нахождение аналитического решения. Цель — это математическая функция или формула, входными данными которой являются четыре положительных целых числа: m — модуль, a и b — классы конгруэнции простых чисел mod m, а x — верхний предел размера простых чисел. Формула должна показать нам, насколько часто за a следует b среди всех простых чисел меньше x. Если бы мы обладали такой формулой, мы бы могли раскрасить все квадраты в матрице последовательных чисел $inline$ без необходимости даже вычислять сами простые числа до x.

Описание поведения всех простых чисел до x — намного более сложная задача, чем взятие выборки из простых чисел по соседству с x. Аналитический подход сложен и по другим причинам: он требует идей, а не просто циклов вычислений ЦП. Но и награда потенциально может оказаться намного ценнее. Например, вычислив уравнение $A = \pi r^2$ , мы получаем истинные значения для всех окружностей, то, чего нам не может дать конечное количество вычислений (с конечным приближением к $\pi$ ). Это обещает нам не только получение строгих решений, но возникновение озарений.

Увы, мне не удалось получить озарение от чтения анализа Лемке-Оливера и Соундарараджана. Виноваты в основном зияющие пробелы в моих знаниях аналитической теории чисел, но я думаю, что будет честным сказать, что в некоторых частях статьи математика становится довольно устрашающей. Представленное ниже уравнение является Основной Гипотезой Лемке-Оливера и Соундарараджана. (Я немного изменил её запись и упростил один аспект уравнения: оригинал применим к ряду из r последовательных простых чисел, но в моей версии описываются только пары, то есть $inline$ .)

$\pi(x; m, a, b) = \frac{\mathrm{li}(x)}{\phi(m)^2}\left(1 + c_1(m; a, b)\frac{\log \log x}{\log x} + c_2(m; a, b) \frac{1}{\log x} + O\Big( \frac{1}{(\log x)^{7/4}} \Big) \right)$

Мне кажется, я достаточно хорошо понимаю то, что здесь происходит, чтобы предложить свои пояснения. Слева от знака равенства $\pi(x; m, a, b)$ обозначает считающую функцию, при этом $\pi(x)$ считает простые числа до $inline$ , $\pi(x; m, a, b)$ — это число пар последовательных простых чисел $inline$ , попадающих в классы конгруэнции $inline$ и $inline$ . Справа от знака равенства основной коэффициент $\mathrm{li}(x) / \phi(m)^2$ является средним или ожидаемым количеством пар, если бы простые числа были бы случайным образом равномерно распределены без корреляций между последовательными простыми числами; $\mathrm{li}(x)$ — это логарифмический интеграл $inline$ , аппроксимация $\pi(x)$ , а $\phi(m)^2$ — это функция Эйлера, считающая квадрат числа возможных классов конгруэнции для $m$, или, иными словами, количество элементов в матрице последовательных чисел.

Главный член в больших скобках — это просто $inline$ , а поэтому он присоединяет значение основного коэффициента $\mathrm{li}(x) / \phi(m)^2$ ; поэтому среднее число пар $inline$ становится первым приближением к считающей функции. Три следующих члена используются как уточнения этого первого приближения; для большого $inline$ они должны становиться всё меньше, потому что $\log \log x / \log x \gt 1 / \log x \gt 1 / (\log x)^{7/4}$ при $x \gt e^e \approx 15$ .

А как насчёт коэффициентов этих трёх уточняющих членов? Запись $O \cdot$ для наименьшего члена означает, что нас будет интересовать только порядок величины члена, который для большого $inline$ будет малым. Коэффициент $inline$ при $inline$ принимает следующий вид:

$c_1(m; a, b) = \frac{1}{2} - \frac{\phi(m)}{2} (\#\{a \equiv b \bmod m\})$

Выражение $\#\{a \equiv b \bmod m\}$ считает количество случаев, когда $inline$ и $inline$ принадлежат к одному классу конгруэнции mod $inline$ . То есть важность члена (если я понял правильно) заключается в уменьшении общего количества вдоль диагонали матрицы, где $a \equiv b \bmod m$ .

Что касается коэффициента $inline$ , то Лемке-Оливер и Соунарараджан указывают, что «в общем случае, [он] кажется сложным». И они правы. На этом моменте я должен посоветовать читателям, желающим узнать больше, прочитать оригинал статьи самостоятельно.

Сложность математического описания расстраивает меня, но очень часто просто сформулированная задача требует глубокого и сложного решения. У меня остаётся только надежда на то, что после дополнительной работы часть технических подробностей можно будет отбросить, а основные идеи будут более ясными. Ну а пока мы по-прежнему можем исследовать восхитительный и долго скрывавшийся от нас уголок теории чисел с помощью простейших вычислительных инструментов, а также капли графики.

«Бог, возможно, и не играет с Вселенной в кости, но с простыми числами происходит что-то странное», — так сказал Пал Эрдёш и/или Марк Кац, с небольшой помощью Карла Померанса. Странность проявляется страньше всего, когда мы играем в кости с помощью простых чисел.

Дополнение. Я упомянул выше, что распределение простых чисел по модулю 7 кажется более плоским или более приближенным к равномерному, чем результат бросков правильной кости. Джон Д. Кук провёл с данными проверку хи-квадрат и оказалось, что они вписываются в равномерное распределение слишком хорошо, чтобы это было правдоподобным результатом случайного процесса. В его первом посте рассматривается конкретный случай простых чисел по модулю 7; в его втором посте рассматриваются другие модули.

Справочные материалы

Ash, Avner, Laura Beltis, Robert Gross, and Warren Sinnott. 2011. Frequencies of successive pairs of prime residues. Experimental Mathematics 20(4):400–411.
Chebyshev, Pafnuty Lvovich. 1853. Lettre de M. le Professeur Tchébychev à M. Fuss sur un nouveaux théorème relatif aux nombres premiers contenus dans les formes 4n + 1 et 4n + 3. Bulletin de la Class Physico-mathematique de l’Academie Imperiale des Sciences de Saint-Pétersbourg 11:208. Google Books

Cramér, Harald. 1936. On the order of magnitude of the difference between consecutive prime numbers. Acta Arithmetica 2:23–46. PDF

Derbyshire, John. 2002. Chebyshev’s bias.

Granville, Andrew. 1995. Harald Cramér and the distribution of prime numbers. Harald Cramér Symposium, Stockholm, 1993. Scandinavian Actuarial Journal 1:12–28. PDF

Granville, Andrew, and Greg Martin. 2004. Prime number races. arXiv

Hamza, Kais, and Fima Klebaner. 2012. On the statistical independence of primes. The Mathematical Scientist 37:97–105.

Klarreich, Erica. 2016. Mathematicians discover prime conspiracy. Quanta.

Knapowski, S., and P. Turán. 1977. On prime numbers? 1 resp. 3 mod 4. In Number Theory and Algebra: Collected Papers Dedicated to Henry B. Mann, Arnold E. Ross, and Olga Taussky-Todd, pp. 157–165. Edited by Hans Zassenhaus. New York: Academic Press.

Ko, Chung-Ming. 2002. Distribution of the units digit of primes. Chaos Solitons Fractals 13(6):1295–1302.

Lamb, Evelyn. 2016. Peculiar pattern found in ‘random’ prime numbers. Nature doi:10.1038/nature.2016.19550.

Lemke Oliver, Robert J., and Kannan Soundararajan. 2016 preprint. Unexpected biases in the distribution of consecutive primes. arXiv

Odlyzko, Andrew, Michael Rubinstein, and Marek Wolf. 1999. Jumping champions. Experimental Mathematics 8(2):107–118.

Rubinstein, Michael, and Peter Sarnak. 1994. Chebyshev’s bias. Experimental Mathematics 3:173–197. Project Euclid

Tao, Terrence. Structure and randomness in the prime numbers. PDF

Tags:

Hubs:

If this publication inspired you and you want to support the author, do not hesitate to click on the button