Когда Пифагор плыл по реке Хуанхэ, он увидел у берега, в лодке, задремавшего рыбака, в конической шляпе и с бамбуковой удочкой в руках.
Памятуя о том, что на Хабрахабр заглядывают люди разной математической подготовки, — однако, в поле интересов которых вполне может попадать тема линейных преобразований, — в связи с её практической значимостью, — я попробую рассказать об этом максимально доступно.

Треугольные очертания лодки, шляпы и удочки над водой настолько поразили философа-математика, что он застыл как заворожённый.
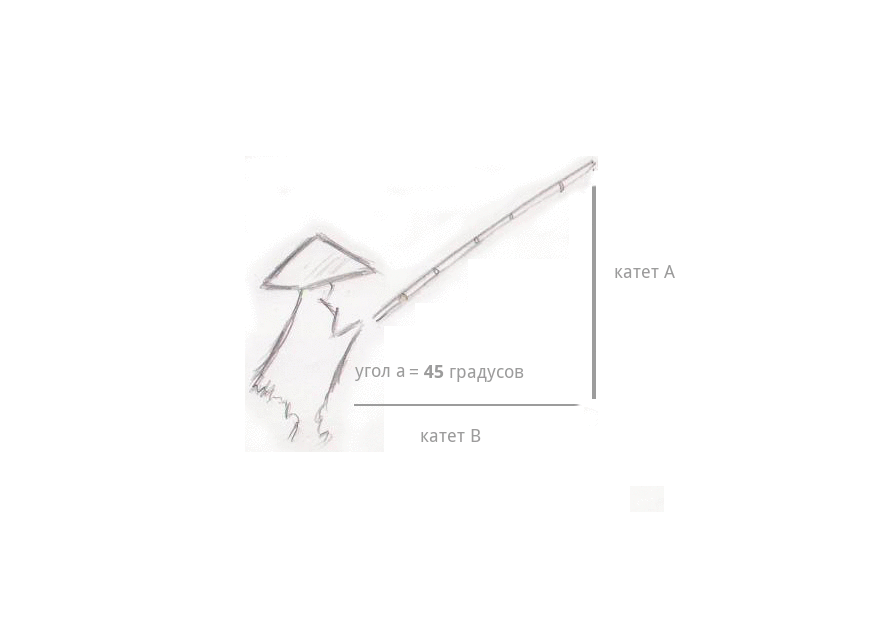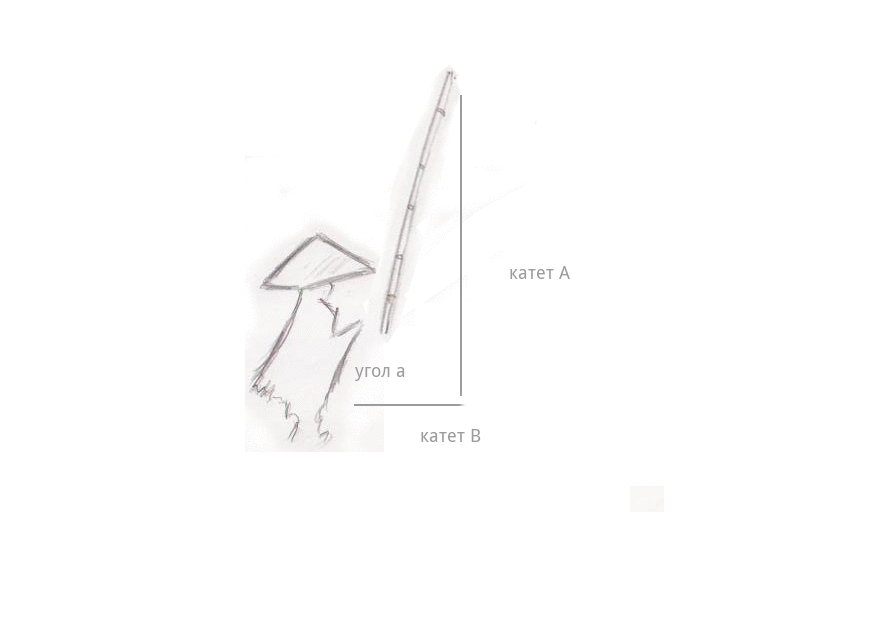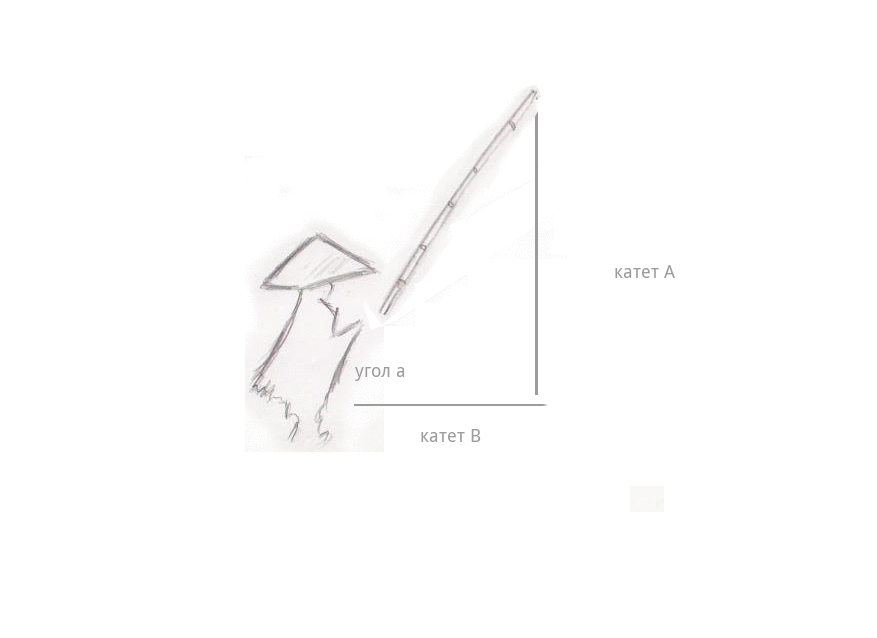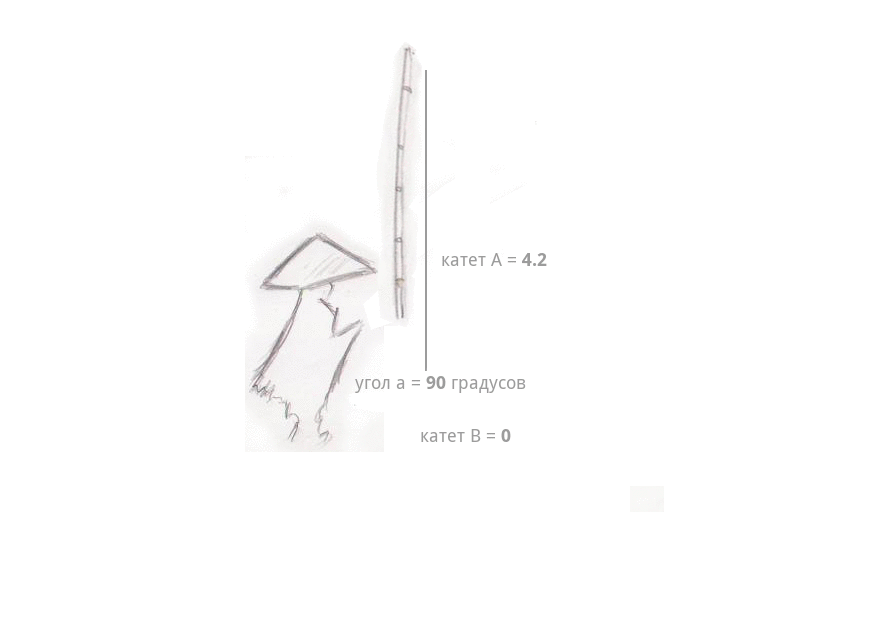
Удочка рыбака аккуратно зависла над гладью вод Жёлтой Реки под углом, равным 45 градусам.
Лёгкий туман стелился над водой… и вдруг — поклёв. Рыбак потянул удочку, и она стала быстро набирать высоту, длина лески (катет А) стала расти на глазах, а расстояние от рыбака до самой лески стало уменьшаться (катет B). И самое интересное — длина самой удочки совсем не изменилась — телескопических удочек ещё не было, — даже когда она описала в воздухе дугу и оказалась почти над головой рыбака, под углом 90 градусов. Длина лески сравнялась с длиной удочки — катушки тогда уже были, — а расстояние между рыбаком и леской изменилось до 0, леска оказалась в руках рыбака.
Последний момент очень важен для понимания того, что происходит при умножении вектора-удочки на матрицу поворота.
Вспомним теорему Пифагора: квадрат длины удочки равен сумме квадратов катетов — самой лески и расстоянию между рыбаком и тем местом, где леска погружена в воду — С^2=А в квадрате + B в квадрате.
Представим, что длина удочки 4.2, длина (или высота над водой) лески 3, расстояние между рыбаком и местом, где леска погружена в воду тоже 3.
1) найдём то, как соотносится между собой длина лески с длиной удочки — синус угла а.
2) найдём то, как соотносится длина отрезка между рыбаком и местом погружения лески с длиной удочки — косинус а. Считаем:
А теперь порассуждаем
Что будет если катет А разделить на sin(a)?! т.е.:
Получаем длину удочки — гипотенузу.
А если мы умножим катет А на sin(а)?!
Отметим это расстояние на гипотенузе — 2.1.
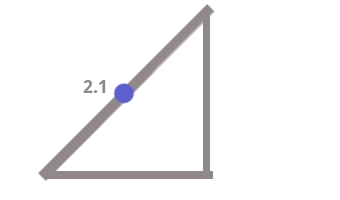
На оставшееся расстояние также приходится — 2.1, так как очевидно:
Это означает, то как в текущий момент времени синус и косинус делят гипотенузу. Поскольку квадрат гипотенузы это 4.2*4.2, то вопрос: что будет если 4.2 умножить на 2.1?! На ту самую её часть, с которой связан один из катетов:
Тоже самое для второго катета.
Нашли катеты. И убедились в том, что со времён Пифагора ничего не изменилось.
Теперь ещё раз осуществим умножение катета А на sin(a), катета B на cos(a).
Суммируем:
или
Снова получили число равное длине удочки… и мы вплотную подобрались к матрице поворота.

(изображение из Википедии. Ссылка на статью)
Возьмём её нижнюю часть — получение точки y:
И сравним с вычислениями выше:
Как две капли воды. Y в нашем случае окажется равным 4.2.
Если применить первую часть формулы к вычислениям, то получим:
Иными словами случится так:
x станет 0 — рыбак поймает леску.
y станет 4.2 — леска сравняется с длиной удочки.
Помним, что для вычисления x синус и косинус меняются местами.
Ф в данном случае равно 45 градусам (Ф = 0.7 ) и при таком угле синус и косинус равны, что удобно для примера. В остальных случаях очевидно величины для синуса и косинуса будут другие. Например, для 40 градусов: cosdegree(40) = 0,7660444431, sindegree(40) = 0,6427876097 (если вы не согласны, обращайтесь в Яндекс, я пользовался его калькулятором).
Применяя формулу к новым значениям x,y несколько раз — в цикле, наглядно увидим движение по окружности, каждый раз на 45 градусов.
Если требуется сдвинуть вектор-удочку на один градус, то его и подставляем в формулу на место Ф.
Как происходит вычисление тригонометрических функций?!
Как известно, для вычисления косинуса и синуса угла обычно используются готовые функции. Согласно информации по ссылке вычисление и точность зависят от системы. Для unix-систем есть по крайней мере два варианта: функция, написанная в недрах компании IBM и встроенная инструкция fsin на Ассемблере. Есть также библиотека fdlibm с достаточно наглядным кодом и комментариями, по которым видно, что синус и косинус вычисляются в этой библиотеке через число pi.
Если у вас на компьютере есть веб-сервер и интерпретатор языка PHP, то можно поэкспериментировать со следующим кодом, который вращает блок CSS div:
Если немного изменить матрицу, то можно получить вращение по спирали или сделать из точки маятник.
Памятуя о том, что на Хабрахабр заглядывают люди разной математической подготовки, — однако, в поле интересов которых вполне может попадать тема линейных преобразований, — в связи с её практической значимостью, — я попробую рассказать об этом максимально доступно.
Продолжим историю

Треугольные очертания лодки, шляпы и удочки над водой настолько поразили философа-математика, что он застыл как заворожённый.
Удочка рыбака аккуратно зависла над гладью вод Жёлтой Реки под углом, равным 45 градусам.
Лёгкий туман стелился над водой… и вдруг — поклёв. Рыбак потянул удочку, и она стала быстро набирать высоту, длина лески (катет А) стала расти на глазах, а расстояние от рыбака до самой лески стало уменьшаться (катет B). И самое интересное — длина самой удочки совсем не изменилась — телескопических удочек ещё не было, — даже когда она описала в воздухе дугу и оказалась почти над головой рыбака, под углом 90 градусов. Длина лески сравнялась с длиной удочки — катушки тогда уже были, — а расстояние между рыбаком и леской изменилось до 0, леска оказалась в руках рыбака.

Последний момент очень важен для понимания того, что происходит при умножении вектора-удочки на матрицу поворота.
Ностальгируем и думаем дальше...
Вспомним теорему Пифагора: квадрат длины удочки равен сумме квадратов катетов — самой лески и расстоянию между рыбаком и тем местом, где леска погружена в воду — С^2=А в квадрате + B в квадрате.
Представим, что длина удочки 4.2, длина (или высота над водой) лески 3, расстояние между рыбаком и местом, где леска погружена в воду тоже 3.
Окунёмся в поиски
1) найдём то, как соотносится между собой длина лески с длиной удочки — синус угла а.
2) найдём то, как соотносится длина отрезка между рыбаком и местом погружения лески с длиной удочки — косинус а. Считаем:
sin(a) = 3/ 4.2= 0.7
cos(a) = 3/ 4.2 = 0.7
А теперь порассуждаем
Что будет если катет А разделить на sin(a)?! т.е.:
3/0.7= 4.2
Получаем длину удочки — гипотенузу.
А если мы умножим катет А на sin(а)?!
3*0.7= 2.1
Отметим это расстояние на гипотенузе — 2.1.

На оставшееся расстояние также приходится — 2.1, так как очевидно:
4.2-2.1=2.1
Это означает, то как в текущий момент времени синус и косинус делят гипотенузу. Поскольку квадрат гипотенузы это 4.2*4.2, то вопрос: что будет если 4.2 умножить на 2.1?! На ту самую её часть, с которой связан один из катетов:
4.2*2.1 = 9, (корень: 3)
Тоже самое для второго катета.
Нашли катеты. И убедились в том, что со времён Пифагора ничего не изменилось.
Далее
Теперь ещё раз осуществим умножение катета А на sin(a), катета B на cos(a).
3*0.7= 2,1
3*0.7 = 2,1
Суммируем:
2.1 + 2.1 =4.2
или
3*0.7 + 3*0.7 =4.2
Снова получили число равное длине удочки… и мы вплотную подобрались к матрице поворота.
Напомню формулу

(изображение из Википедии. Ссылка на статью)
Возьмём её нижнюю часть — получение точки y:
y=x*sin(Ф)+y*cos(Ф)
И сравним с вычислениями выше:
3*0.7 + 3*0.7 = 4.2
y=x*sin(Ф)+y*cos(Ф)
Как две капли воды. Y в нашем случае окажется равным 4.2.
Если применить первую часть формулы к вычислениям, то получим:
3*0.7 — 3*0.7 = 0
Иными словами случится так:
x станет 0 — рыбак поймает леску.
y станет 4.2 — леска сравняется с длиной удочки.
Помним, что для вычисления x синус и косинус меняются местами.
Ф в данном случае равно 45 градусам (Ф = 0.7 ) и при таком угле синус и косинус равны, что удобно для примера. В остальных случаях очевидно величины для синуса и косинуса будут другие. Например, для 40 градусов: cosdegree(40) = 0,7660444431, sindegree(40) = 0,6427876097 (если вы не согласны, обращайтесь в Яндекс, я пользовался его калькулятором).
В итоге
Применяя формулу к новым значениям x,y несколько раз — в цикле, наглядно увидим движение по окружности, каждый раз на 45 градусов.
Если требуется сдвинуть вектор-удочку на один градус, то его и подставляем в формулу на место Ф.
Как происходит вычисление тригонометрических функций?!
Как известно, для вычисления косинуса и синуса угла обычно используются готовые функции. Согласно информации по ссылке вычисление и точность зависят от системы. Для unix-систем есть по крайней мере два варианта: функция, написанная в недрах компании IBM и встроенная инструкция fsin на Ассемблере. Есть также библиотека fdlibm с достаточно наглядным кодом и комментариями, по которым видно, что синус и косинус вычисляются в этой библиотеке через число pi.
А вдруг автор этой статьи все придумал?
Если у вас на компьютере есть веб-сервер и интерпретатор языка PHP, то можно поэкспериментировать со следующим кодом, который вращает блок CSS div:
Файл index.php
Заголовок спойлера
<?php
if (isset($_GET['ok'])) {
$x= $_GET['x']*cos(1)-$y=$_GET['y']*sin(1);
$y= $_GET['x']*sin(1)+$y=$_GET['y']*cos(1);
}
?>
<style>
#rotation_martix {
position: absolute;
top: <?=$x+300?>px;
left: <?=$y+300?>px;
background-color: #999;
width: 10px;
height: 10px;
}
</style>
< div id="rotation_martix">
</ div>
<form method="GET" >
<input type="submit" name="ok" value="ok">
<input type="text" name="x" value="<?=$x?>">
<input type="text" name="y" value="<?=$y?>">
</form>
Если немного изменить матрицу, то можно получить вращение по спирали или сделать из точки маятник.