
Введение
Беспоисковый метод — простой, надёжный и универсальный метод расчёта настроек субоптимальных регуляторов, включая и такие алгоритмы как ПД, ПДД и ПИДД [1].
Однако, приведенная в [1] программная реализация данного метода имеет ряд недостатков, что затрудняет его применение в микропроцессорных регулирующих приборах.
Среди недостатков можно выделить такие:
Неоднозначность в определении диапазона рабочих частот, которая, даже при наличии сглаживающего звена в структуре передаточной функции регулятора, может привести к отрицательным значениям настроек;
В работе [1] для реализации беспоискового метода расчёта регуляторов рассматривается передаточная функция объекта вида:
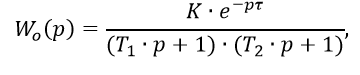
что при второй степени оператора p в знаменателе ограничивает точность динамической идентификации объекта управления [2].
Постановка задачи:
1. Средствами высокоуровневого языка программирования Python определять по КЧХ субоптимального регулятора максимальное и минимальное значение частот так, чтобы, при максимуме частоты, мнимая и действительная часть передаточной функции были положительными;
2. Средствами библиотеки scipy. optimize высокоуровневого языка программирования Python найти по передат��чной функции субоптимального регулятора настройки регулятора, а средствами библиотеки scipy. integrate получить переходные характеристики замкнутой системы регулирования;
3. Для более точной идентификации объекта, использовать в расчётах передаточную функцию, имеющую третью степень оператора p в знаменателе;
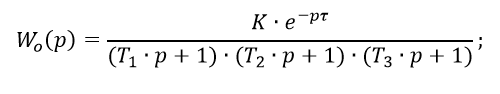
4. Сравнить переходные характеристики замкнутой системы, полученные поисковым [3] и беспоисковым методами;
5. Построить с использованием беспоискового метода переходную характеристику для ПИДД алгоритма, сравнить её по интегральному квадратичному критерию качества регулирования с ПИД алгоритмом.
Теория
Рассмотрим структурную схему одноконтурной системы регулирования:
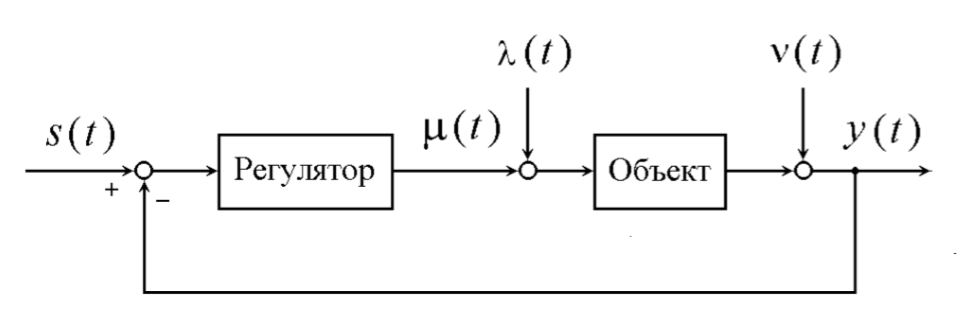
Алгоритм оптимального регулятора зависит от точки приложения ступенчатого входного воздействия. На следующем рисунке показаны переходные характеристики замкнутой системы относительно воздействий: а) ─ задающегоs(t); б) ─ внешнего v(t); в) ─ внутреннего λ(t):
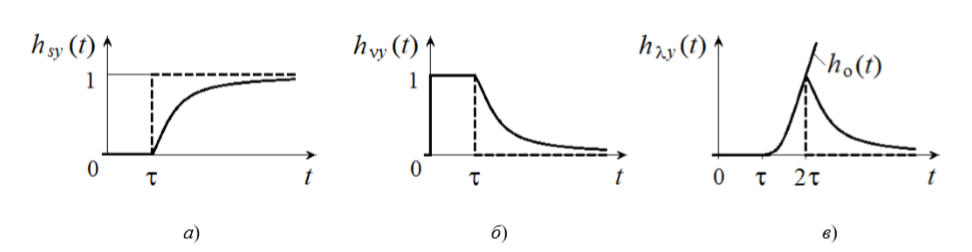
Оптимальный регулятор по истечении времени запаздывания τ должен полностью воспроизводить заданное на вход системы единичное воздействие s(t)=1. Для этого передаточная функция замкнутой системы должна быть равна:
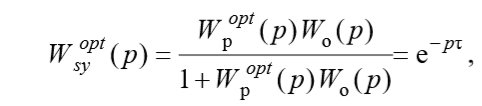
из приведенного уравнения получим соотношение для передаточной функции оптимального регулятора:
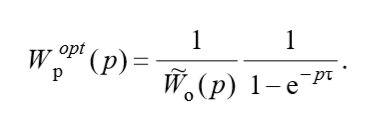 (1)
(1)В комплексно-частотной характеристике (1) имеются разрывы с периодом τ, что приводит к потере устойчивости системы. Поэтому, для получения передаточной функции субоптимального регулятора, нужно применить сглаживание при помощи простейшего инерционного элемента с передаточной функцией:
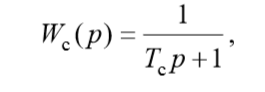
тогда желаемую передаточную функцию субоптимальной замкнутой системы можно представить в виде:
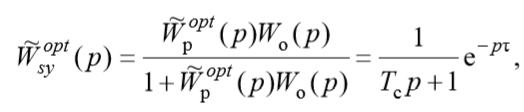
а передаточная функция субоптимального регулятора —
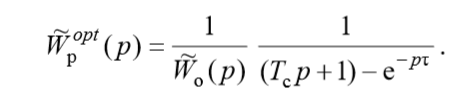 (2)
(2)Использование передаточной функции субоптимального регулятора (2) может не дать желаемого переходного процесса, поскольку структура субоптимального регулятора зависит от структуры передаточной функции объекта.
Например, при регулировании температуры перегретого пара, объект имеет экстремальную переходную характеристику. В этом случае в качестве сглаживания следует выбирать интегро-дифференцирующее (ИД) звено с передаточной функцией:
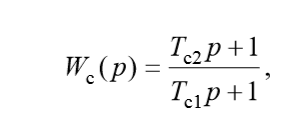
тогда передаточная функция субоптимального регулятора запишется как:
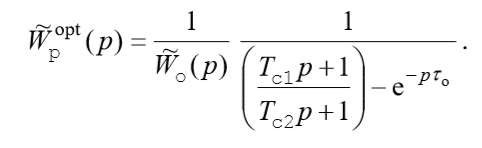 (3)
(3)Имея передаточные функции субоптимальных регуляторов (2),(3), можно перейти к рассмотрению беспоискового метода определения настроек.
Расчет оптимальных настроек линейных регуляторов беспоисковым методом [1]:
Приближение методом наименьших квадратов частотных характеристик субоптимальных (2) или (3) регуляторов выполним на примере ПИДД и ПИД регуляторов, имеющих четыре c1,c2,c3,c4 и три c1,c2,c3 параметра настройки соответственно.
Частными случаями ПИД регулятора будут являться П, ПИ, ПД и ПДД законы регулирования. Для П регулятора необходимо приравнять к 0 параметры настройки, c2,c3,c4 для ПИ ― c3,c4, для ПД ―c2,c4 и для ПДД c2.
КЧХ линейного ПИДД регулятора представим в виде:
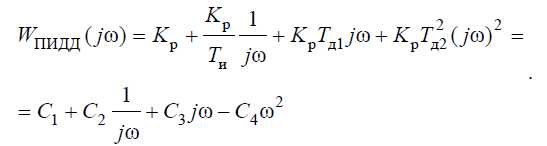 (4)
(4)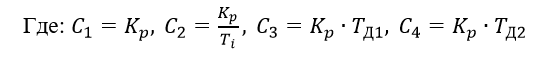
Запишем сумму квадратов невязок для N векторов частотных характеристик для всех типов регуляторов
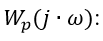
Реализация беспоискового метода средствами Python
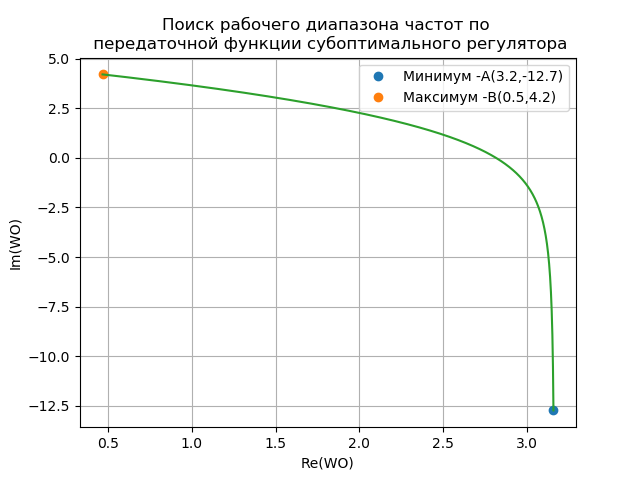
Определение по КЧХ субоптимального регулятора максимального и минимального значения рабочей частоты:
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import quad
from scipy.optimize import *
import matplotlib.pyplot as plt
T1=14;T2=18;T3=28;T=15;K=0.9;tau=6.4#Параметры объекта (при адаптивном регулировании поступают из модели объекта )
fmin=0.004# Варьирование минимальным значением частоты
fmax=0.08#Варьирование максимальным значением частоты
df=0.0001#Швг по частоте
n=np.arange(fmin,fmax,df)# Найденный диапазон
def W(w):#Передаточная функция объекта
j=(-1)**0.5
return ((K*(np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))))
def WO(w):#Передаточная функция субоптимального регулятора с коррекцией
j=(-1)**0.5
return (1/(K*(T*j*w+1-np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))))
def ReWO(w):#Действительная часть передаточной функции субоптимального регулятора
j=(-1)**0.5
return WO(w).real
def ImWO(w):#Мнимая часть передаточной функции субоптимального регулятора
j=(-1)**0.5
return WO(w).imag
S1=[ReWO(w) for w in n]
S2=[ImWO(w) for w in n]
plt.title("Поиск рабочего диапазона частот по \n передаточной функции субоптимального регулятора")
plt.xlabel("Re(WO)")
plt.ylabel("Im(WO)")
plt.plot(ReWO(min(n)),ImWO(min(n)),'o',label='Минимум -А(%s,%s)'%(round(ReWO(min(n)),1),round(ImWO(min(n)),1)))
plt.plot(ReWO(max(n)),ImWO(max(n)),'o',label='Максимум -B(%s,%s)'%(round(ReWO(max(n)),1),round(ImWO(max(n)),1)))
plt.plot(S1,S2)
plt.grid(True)
plt.legend(loc='best')
plt.show()После нахождения при помощи переменных fmin, fmax, df необходимого участка КЧХ получим:
Сравнительный анализ поискового и беспоискового методов на примере с ПИД регулятором и передаточной функции объекта с третьей степенью оператора p в знаменателе:
Для сравнительного анализа беспоискового и поискового метода воспользуемся результатами работы поискового метода, приведенного в моей публикации [3] для параметров объекта T1=14; T2=18;T3=28; K=0.9; tau=6.4, которые и были использованы при решении первой задачи.
Листинг поискового метода [3]
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import quad
from scipy.optimize import *
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
T1=14;T2=18;T3=28;K=0.9;tau=6.4# Постоянные времени, статический коэффициент передачи, время запаздывания
m=0.366;m1=0.221# Запас устойчивости
n= np.arange(0.001,0.15,0.0002)#Массив частот для плоскости Kr-Ki
n1=np.arange(0.00001,0.12,0.0001)#Массив частот для графика Ki=f(w)
n2=np.arange(0.0002,0.4,0.0001)#Массив частот для построения АЧХ
def WO(m,w):#Передаточная функция объекта
j=(-1)**0.5
return K*np.exp(-tau*(-m+j)*w)/((T1*(-m+j)*w+1)*(T2*(-m+j)*w+1)*(T3*(-m+j)*w+1))
def WR(w,Kr,Ti,Td):#Передаточная функция регулятора
j=(-1)**0.5
return Kr*(1+1/(j*w*Ti)+j*w*Td)
def ReW(m,w):#Действительная часть передаточной функции
j=(-1)**0.5
return WO(m,w).real
def ImW(m,w):#Мнимая часть передаточной функции
j=(-1)**0.5
return WO(m,w).imag
def A0(m,w):#Вспомогательная функция
return -(ImW(m,w)*m/(w+w*m**2)+ReW(m,w)/(w+w*m**2))
def Ti(alfa,m,w):#Коэффициент регулятора
return (-ImW(m,w)-(ImW(m,w)**2-4*((ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m)*A0(m,w)))**0.5)/(2*(ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m))
def Ki(alfa,m,w):#Коэффициент регулятора
return 1/(w*Ti(alfa,m,w)**2*alfa*(m*ReW(m,w)+ImW(m,w))-Ti(alfa,m,w)*ReW(m,w)+(m*ReW(m,w)-ImW(m,w))/(w+w*m**2))
def Kr(alfa,m,w):#Коэффициент регулятора
if Ki(alfa,m,w)*Ti(alfa,m,w)<0:
z=0
else:
z=Ki(alfa,m,w)*Ti(alfa,m,w)
return z
def Kd(alfa,m,w):#Коэффициент регулятора
return alfa*Kr(alfa,m,w)*Ti(alfa,m,w)
alfa=0.2
Ki_1=[Ki(alfa,m1,w) for w in n]
Kr_1=[Kr(alfa,m1,w) for w in n]
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n для alfa=%s"%alfa)
plt.axis([0.0, round(max(Kr_3),4), 0.0, round(max(Ki_3),4)])
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
alfa=0.7
Ki_1=[Ki(alfa,0.221,w) for w in n]
Kr_1=[Kr(alfa,0.221,w) for w in n]
Ki_2=[Ki(alfa,0.366,w) for w in n]
Kr_2=[Kr(alfa,0.366,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]
plt.figure()
plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)])
plt.title("Плоскость настроечных параметров ПИД регулятора\n для alfa=%s"%alfa)
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
alfa=1.2
Ki_1=[Ki(alfa,0.221,w) for w in n]
Kr_1=[Kr(alfa,0.221,w) for w in n]
Ki_2=[Ki(alfa,0.366,w) for w in n]
Kr_2=[Kr(alfa,0.366,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n для alfa=%s"%alfa)
plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)])
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n для запаса устойчивости m=%s"%m)
alfa=0.2
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=0.4
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=0.7
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=1.2
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
plt.axis([0.0, round(max(Kr_2),3), 0.0, round(max(Ki_2),3)])
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title("График Ki=f(w)")
Ki_1=[Ki(0.2,m,w) for w in n1]
Ki_2=[Ki(0.7,m,w) for w in n1]
Ky=max([round(max(Ki_1),4),round(max(Ki_2),4)])
plt.axis([0.0,round(max(n1),4),0.0, Ky])
plt.plot(n1, Ki_1,label='allfa=Td/Ti =0.2, запас устойчивости m=0.366')
plt.plot(n1, Ki_2,label='allfa=Td/Ti =0.7, запас устойчивости m=0.366')
plt.legend(loc='best')
plt.grid(True)
maxKi=max( [Ki(0.7,m,w) for w in n1])
wa=round([w for w in n1 if Ki(0.7,m,w)==maxKi][0],3)
Ki1=round(Ki(0.7,m,wa),3)
Kr1=round(Kr(0.7,m,wa),3)
Ti1=round(Kr1/Ki1,3)
Td1=round(0.7*Ti1,3)
d={}
d[0]= "Настройки №1 ПИД регулятора (wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr1,Ti1,Ki1,Td1)
print(d[0])
maxKi=max( [Ki(0.2,m,w) for w in n1])
wa=round([w for w in n1 if Ki(0.2,m,w)==maxKi][0],3)
Ki2=round(Ki(0.2,m,wa),3)
Kr2=round(Kr(0.2,m,wa),3)
Ti2=round(Kr2/Ki2,3)
Td2=round(0.2*Ti2,3)
d[1]= "Настройки №2 ПИД регулятора(wa =%s,m=0.366,alfa=0.2): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr2,Ti2,Ki2,Td2)
print(d[1])
wa=fsolve(lambda w:Ki(0.7,m,w)-0.14,0.07)[0]
wa=round(wa,3)
Ki3=round(Ki(0.7,m,wa),3)
Kr3=round(Kr(0.7,m,wa),3)
Ti3=round(Kr3/Ki3,3)
Td3=round(0.7*Ti3,3)
d[2]= "Настройки №3 ПИД регулятора(wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr3,Ti3,Ki3,Td3)
print(d[2])
def Wsys(w,Kr,Ti,Td):
j=(-1)**0.5
return (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td)))
Wsys_1=[abs(Wsys(w,Kr1,Ti1,Td1)) for w in n2]
Wsys_2=[abs(Wsys(w,Kr2,Ti2,Td2)) for w in n2]
Wsys_3=[abs(Wsys(w,Kr3,Ti3,Td3)) for w in n2]
plt.figure()
plt.title("Амплитудно-частотные характеристики замкнутой АСР \n с ПИД регулятором")
plt.plot(n2, Wsys_1,label=' Для настройки №1 ПИД регулятора')
plt.plot(n2, Wsys_2,label=' Для настройки №2 ПИД регулятора')
plt.plot(n2, Wsys_3,label=' Для настройки №3 ПИД регулятора')
plt.legend(loc='best')
plt.grid(True)
def ReWsys(w,t,Kr,Ti,Td):
return(2/np.pi)* (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td))).real*(np.sin(w*t)/w)
def h(t,Kr,Ti,Td):
return quad(lambda w: ReWsys(w,t,Kr,Ti,Td),0,0.6)[0]
tt=np.arange(0,300,3)
h1=[h(t,Kr1,Ti1,Td1) for t in tt]
h2=[h(t,Kr2,Ti2,Td2) for t in tt]
h3=[h(t,Kr3,Ti3,Td3) for t in tt]
I1=round(quad(lambda t: h(t,Kr1,Ti1,Td1), 0,200)[0],3)
I11=round(quad(lambda t: h(t,Kr1,Ti1,Td1)**2,0, 200)[0],3)
I2=round(quad(lambda t: h(t,Kr2,Ti2,Td2), 0,200)[0],3)
I21=round(quad(lambda t: h(t,Kr2,Ti2,Td2)**2,0, 200)[0],3)
I3=round(quad(lambda t: h(t,Kr3,Ti3,Td3), 0,200)[0],3)
I31=round(quad(lambda t: h(t,Kr3,Ti3,Td3)**2,0, 200)[0],3)
print("Линейный интегральный критерий качества I1 =%s (настройки №1)"%I1)
print("Квадратичный интегральный критерий качества I2 =%s (настройки №1"%I11)
print("Линейный интегральный критерий качества I1 =%s (настройки №2 )"%I2)
print("Квадратичный интегральный критерий качества I2 =%s (настройки №2)"%I21)
print("Линейный интегральный критерий качества I1 =%s (настройки №3 )"%I3)
print("Квадратичный интегральный критерий качества I2 =%s (настройки №3)"%I31)
Rez=[I1+I11,I2+I21,I3+I31]
In=Rez.index(min(Rez))
print("Оптимальные параметры по интегральным критериям :\n %s"%d[In])
plt.figure()
plt.title("Переходные характеристики замкнутой АСР \n с ПИД регулятором")
plt.plot(tt,h1,'r',linewidth=1,label=' Для настройки №1 ПИД регулятора')
plt.plot(tt,h2,'b',linewidth=1,label=' Для настройки №2 ПИД регулятора')
plt.plot(tt,h3,'g',linewidth=1,label=' Для настройки №3 ПИД регулятора')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Результаты текстового вывода:
Настройки №1 ПИД регулятора (wa =0.066,m=0.366,alfa=0.7): Kr=4.77; Ti=21.682; Ki=0.22; Td=15.177
Настройки №2 ПИД регулятора(wa =0.056,m=0.366,alfa=0.2): Kr=2.747; Ti=50.87; Ki=0.054; Td=10.174
Настройки №3 ПИД регулятора (wa =0.085,m=0.366,alfa=0.7): Kr=3.747; Ti=26.387; Ki=0.142; Td=18.471
Линейный интегральный критерий качества I1 =194.65 (настройки №1)
Квадратичный интегральный критерий качества I2 =222.428 (настройки №1
Линейный интегральный критерий качества I1 =179.647 (настройки №2 )
Квадратичный интегральный критерий качества I2 =183.35 (настройки №2)
Линейный интегральный критерий качества I1 =191.911 (настройки №3 )
Квадратичный интегральный критерий качества I2 =204.766 (настройки №3)
Оптимальные параметры по интегральным критериям:
Настройки №2 ПИД регулятора (wa =0.056,m=0.366,alfa=0.2): Kr=2.747; Ti=50.87; Ki=0.054; Td=10.174
Листинг программы для сравнения методов расчёта настроек регуляторов
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import quad
from scipy.optimize import *
import matplotlib.pyplot as plt
T1=14;T2=18;T3=28;T=15;K=0.9;tau=6.4# T постоянная времени А звена
fmin=0.004
fmax=0.08
df=0.0001
n=np.arange(fmin,fmax,df)
def W(w):#Передаточная функция объекта
j=(-1)**0.5
return ((K*(np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))))
def WO(w):#Передаточная функция субоптимального регулятора с А сглаживающим звеном
j=(-1)**0.5
return (1/(K*(T*j*w+1-np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))))
def WR(w,c1,c2,c3):# Передаточная функция ПИД регулятора
j=(-1)**0.5
return (c1+c2/(j*w)+c3*j*w)
def NF(c1,c2,c3):# Расчёт настроек ПИД по минимальному квадрату отклонения от субоптимального регулятора
return sum([((WO(w)).real-WR(w,c1,c2,c3).real)**2+((WO(w)).imag-WR(w,c1,c2,c3).imag)**2 for w in n])
def fun2(x):
return NF(*x)
x0=[1,1,1]
res = minimize(fun2, x0)
time=np.arange(0,300,1)
e1=round(res['x'][0],3)
e2=round(res['x'][1],3)
e3=round(res['x'][2],3)
Kp=round(res['x'][0],3)
Ti=round((res['x'][0]/res['x'][1]),3)
Ki=round((res['x'][0]/Ti),3)
Td=round((res['x'][2]/res['x'][0]),3)
print ("Расчётное значение функции цели для беспоискового метода:",round(res['fun'],3))
print("Настройки ПИД регулятора по беспоисковому методу: Kp=%s; Ti=%s; Ki=%s; Td=%s "%(Kp,Ti,Ki,Td))
def h(t,e1,e2,e3):
return quad(lambda w:(2/np.pi)*(((W(w))*WR(w,e1,e2,e3))/(1+(W(w))*WR(w,e1,e2,e3))).real*(np.sin(w*t)/w),0,max(n))[0]
h1=[h(t,e1,e2,e3) for t in time]
I1=round(quad(lambda t:h(t,e1,e2,e3), 0,300)[0],3)+round(quad(lambda t: h(t,e1,e2,e3)**2,0, 300)[0],3)
Kp=2.747
Ti=50.87
Td=10.174
Ki=round(Kp/Ti,3)
print("Настройки ПИД регулятора по поисковому методу: Kp=%s; Ti=%s; Ki=%s; Td=%s "%(Kp,Ti,Ki,Td))
e1=Kp
e2=Kp/Ti
e3=Td*Kp
print ("Рас��ётное значение функции цели для поискового метода [3]:",round(NF(e1,e2,e3),3))
h2=[h(t,e1,e2,e3) for t in time]
I2=round(quad(lambda t:h(t,e1,e2,e3), 0,300)[0],3)+round(quad(lambda t: h(t,e1,e2,e3)**2,0, 300)[0],3)
plt.title(" Сравнение по качеству регулирования (для ПИД регулятора) \n поискового и беспоискового методов ")
plt.plot(time,h1,'b',linewidth=2,label=' Квадратичный критерий - %s (Беспоисковый метод)'%I1)
plt.plot(time,h2,'g',linewidth=2,label=' Квадратичный критерий - %s (Поисковый метод)'%I2)
plt.legend(loc='best')
plt.grid(True)
plt.show()Получим:
Расчётное значение функции цели для беспоискового метода: 484.254
Настройки ПИД регулятора по беспоисковому методу: Kp=2.22; Ti=42.904; Ki=0.052; Td=27.637
Настройки ПИД регулятора по поисковому методу: Kp=2.747; Ti=50.87; Ki=0.054; Td=10.174
Расчётное значение функции цели для поискового метода [3]: 2723.341
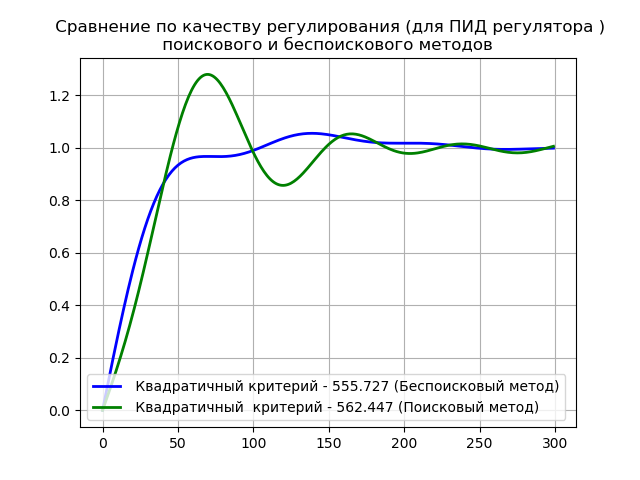
Очевидно, беспоисковый метод проще в реализации и обеспечивает лучшее качество регулирования.
Расчёт настроек и получение переходной характеристики замкнутой системы для нестандартного ПИДД алгоритма регулирования:
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import quad
from scipy.optimize import *
import matplotlib.pyplot as plt
T1=14;T2=18;T3=28;T=15;K=0.9;tau=6.4
fmin=0.004
fmax=0.08
df=0.0001
n=np.arange(fmin,fmax,df)
def W(w):#Передаточная функция объекта
j=(-1)**0.5
return ((K*(np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))))
def WO(w):#Передаточная функция субоптимального регулятора
j=(-1)**0.5
return (1/(K*(T*j*w+1-np.exp(-tau*j*w))/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))))
def WR(w,c1,c2,c3,c4):#Передаточная функция ПИДД регулятора
j=(-1)**0.5
return (c1+c2/(j*w)+c3*j*w-c4*w**2)
def NF(c1,c2,c3,c4):
return sum([((WO(w)).real-WR(w,c1,c2,c3,c4).real)**2+((WO(w)).imag-WR(w,c1,c2,c3,c4).imag)**2 for w in n])
def fun2(x):
return NF(*x)
x0=[1,1,1,1]
res = minimize(fun2, x0)
time=np.arange(0,300,1)
e1=round(res['x'][0],3)
e2=round(res['x'][1],3)
e3=round(res['x'][2],3)
e4=round(res['x'][3],3)
print ("Расчётное значение функции цели для беспоискового метода:",round(res['fun'],3))
def h(t,e1,e2,e3,c4):
return quad(lambda w:(2/np.pi)*(((W(w))*WR(w,e1,e2,e3,e4))/(1+(W(w))*WR(w,e1,e2,e3,e4))).real*(np.sin(w*t)/w),0,max(n))[0]
h1=[h(t,e1,e2,e3,e4) for t in time]
I1=round(quad(lambda t:h(t,e1,e2,e3,e4), 0,300)[0],3)+round(quad(lambda t: h(t,e1,e2,e3,e4)**2,0, 300)[0],3)
plt.title(" Переходная характеристика ПИДД регулятора ")
plt.plot(time,h1,'r',linewidth=2,label=' Квадратичный критерий для ПИДД- %s'%I1)
plt.legend(loc='best')
plt.grid(True)
plt.show()Получим:
Расчётное значение функции цели для беспоискового метода: 0.326
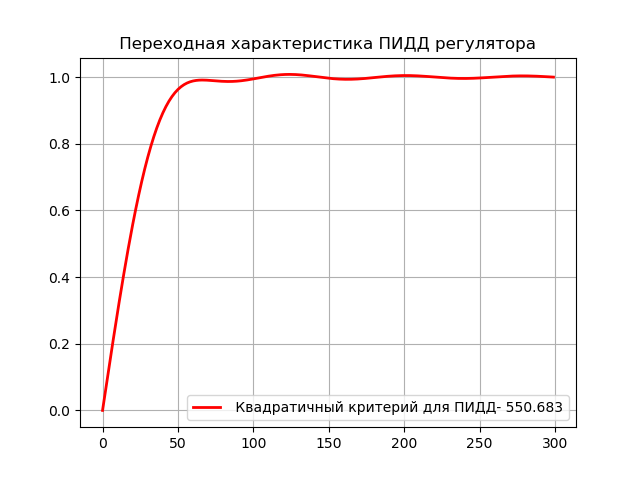
Как и следовало ожидать, ПИДД алгоритм обеспечивает лучшее качество регулирования, чем ПИД, при этом имеет максимальное приближение к субоптимальному регулятору.
Приведенные листинги программ легко могут быть перестроены на регуляторы П, ПИ, ПД и ПДД законов регулирования. Для П регулятора необходимо приравнять к 0 параметры настройки, c2, c3, c4 для ПИ ― c3, c4, для ПД ―c2,c4 и для ПДД c2.
Выводы:
Рассмотрены преимущество реализации на Python беспоискового метода расчета настроек регуляторов на минимум квадратичного критерия.
Ссылки:
1. Беспоисковый метод расчета настроек регуляторов на минимум квадратичного критерия.
2. Динамическая идентификация объектов управления.
3. Оптимизация настроек ПИД регулятора по интегральному критерию качества регулирования.