Как квантовые пары сшивают пространство-время

Первая часть
Брайан Свингл изучал физику в аспирантуре Массачусетского технологического института, когда он решил сходить на парочку занятий по теории струн, чтобы усовершенствовать своё образование – как он сам вспоминает, по принципу «почему бы и нет» – хотя изначально он не обращал внимания на концепции, с которыми он познакомился на этом курсе. Но погружаясь глубже, он начал замечать неожиданные связи с его собственной работой, в которой он использовал т.н. тензорные сети для предсказания свойств экзотических материалов и подход к физике чёрных дыр и квантовой гравитации, взятый из теории струн. «Я понял, что происходит нечто удивительное»,- говорит он.
Тензоры периодически неожиданно возникают в разных областях физики – это математические объекты, которые могут представлять множество чисел сразу. К примеру, вектор скорости – это простейший тензор: он включает как скорость, так и направление. Более сложные тензоры, связанные в сети, можно использовать для упрощения подсчетов для сложных систем, составленных из множества взаимодействующих частей – включая замысловатые взаимодействия огромного количества субатомных частиц, составляющих материю.
Свингл – один из всё возрастающего количества физиков, видящих ценность применения тензорных сетей к космологии. Кроме других преимуществ, это может помочь разрешить продолжающийся спор о сущности пространства-времени. Джон Прескилл, профессор Ричарда Фейнмана по теоретической физике в КалТехе, считал, что многие физики подозревали о глубокой связи между квантовой запутанностью – пугающим дальнодействием, так рассердившим Эйнштейна – и геометрией пространства-времени на мельчайших масштабах. Это продолжается с тех пор, как Джон Уилер шестьдесят лет назад впервые описал пространство-время как пузырящуюся пену. «Если вы будете изучать геометрию на масштабах, сравнимых с планковскими» – на самых коротких возможных расстояниях – «оно всё меньше и меньше выглядит, как пространство-время»,- говорит Прескилл. «Это вообще уже не геометрия, а что-то другое, что-то, что возникает из более фундаментальных вещей».
Физики продолжают бороться с запутанной проблемой того, какой может быть эта более фундаментальная проблема, но они подозревают, что она связана с квантовой информацией. «Когда мы рассуждаем о кодировании информации, мы имеем в виду, что можно разделить систему на части и в ней будет существовать такая корреляция между ними, что я могу узнать что-либо об одной из частей, наблюдая за другой»,- говорит Прескилл. В этом и есть суть запутанности.
Часто говорят о «ткани» пространства-времени и эта метафора приводит к концепции сшивания отдельных нитей вместе для формирования гладкого целого. Эти нити по сути квантовые. «Запутанность – это ткань пространства-времени,- говорит Свингл, в данный момент работающий над исследованиями в Стэнфорде. – Это нить, связывающая всю систему вместе, обеспечивающая отличие общих свойств от свойств отдельных сущностей. Но чтобы на самом деле увидеть интересное совместное поведение, необходимо понять, как распределяется запутанность».
Тензорные сети предоставляют математический инструмент, способный делать именно это. С этой точки зрения, пространство-время возникает из наборов связанных друг с другом узлов сложной сети, где небольшие кусочки квантовой информации стыкуются друг с другом как Lego. Запутанность – это клей, соединяющий сеть. Чтобы понять пространство-время, необходимо для начала рассмотреть запутанность с геометрических позиций, поскольку именно так информация кодируется в огромном количестве взаимодействующих узлов системы.
Много тел, одна сеть
Смоделировать сложную квантовую систему – это вам не шутки; даже классическая система с более чем двумя взаимодействующими частями уже достаточно сложна для моделирования. Когда Исаак Ньютон опубликовал свои Principia [Математические начала натуральной философии] в 1687 году, одной из тем книги стала «задача трёх тел». Задача подсчёта движения двух объектов, например, Солнца и Земли, принимающая во внимание их взаимное притяжение, сравнительно проста. Но если добавить в неё третье тело ��� например, Луну – она превращается из простой задачи с точным решением в хаотичную, где долговременные предсказания требуют мощных вычислительных систем для симуляции приблизительной эволюции системы. И чем больше в системе объектов, тем сложнее расчёты, а их сложность растёт почти линейно – по крайней мере, в классической физике.
Теперь представим квантовую систему с миллиардами атомов, каждый из которых взаимодействует с другими согласно сложным квантовым уравнениям. На этом масштабе сложность, кажется, растёт экспоненциально с ростом количества частиц в системе, поэтому подход к вычислениям с применением грубой силы просто не сработает.
Представьте себе золотой самородок. Он состоит из миллиардов атомов, и все они взаимодействуют друг с другом. Из этих взаимодействий вытекают различные классические свойства металла – цвет, прочность или проводимость. «Атомы – это крохотные штучки, подчиняющиеся квантовой механике, и когда вы собираете их вместе, происходят новые и удивительные вещи»,- говорит Свингл. Но на этих масштабах начинают работать правила квантовой механики. Физикам необходимо точно подсчитать волновую функцию этого самородка, описывающую состояние системы. И эта функция – многоголовая гидра экспоненциальной сложности.
Даже если в самородке будет всего лишь сто атомов и у каждого будет квантовый спин, принимающий одно из двух состояний, вверх или вниз, общее количество возможных состояний составит уже 2100, миллион триллионов триллионов. И с добавлением каждого атома задача ухудшается экспоненциально. (А ещё хуже выходит, когда вы пытаетесь описать что-либо кроме спинов, как должна делать любая реалистичная модель). «Если вы возьмёте всю видимую Вселенную и заполните её лучшими из доступных вам накопителей, лучшими жёсткими дисками, вы сможете хранить на них состояние всего лишь 300 спинов,- говорит Свингл. – Информация есть, но не вся она соответствует физике. Никто никогда не мерил эти числа».
Тензорные сети позволяют физикам сжимать всю содержащуюся в волновой функции информацию и концентрироваться только на тех свойствах, которые можно измерить в эксперименте: как сильно материал преломляет свет, или как хорошо он поглощает звук, или как он проводит электричество. Тензор – это «чёрный ящик», принимающий один набор чисел и выдающий другой. Поэтому можно подключить простую волновую функцию – например, множества не взаимодействующих друг с другом электронов, находящихся в состоянии с наименьшей энергией – и обрабатывать её тензорами снова и снова, пока процесс не выдаст волновую функцию для большой и сложной системы, такой, как миллиарды взаимодействующих в золотом самородке атомов. В результате получится простая диаграмма, представляющая этот сложный самородок – инновация, сравнимая с разработанными Фейнманом в середине 20-го века диаграммами, упростившими представление взаимодействий частиц. И у тензорной сети есть своя геометрия, как и у пространства-времени.
Ключ к упрощению лежит в принципе «локальности». Каждый отдельно взятый электрон взаимодействует только с ближайшими электронами. Запутанность каждого электрона с его соседями даёт набор «узлов» сети. Эти узлы – тензоры и запутанность связывает их вместе. Все эти связанные между собой узлы составляют сеть. Сложные подсчёты становится проще визуализировать. Иногда всё сводится к более простой задаче подсчёта.
Существует множество разных типов тензорных сетей, но среди самых полезных есть одна, известная под аббревиатурой MERA (анзац ренормализации разномасштабной запутанности). Принцип её работы следующий: представьте одномерную линию электронов. Замените восемь разных электронов – обозначим их через A, B, C, D, E, F, G и H – на фундаментальные единицы квантовой информации (кубиты) и запутайте каждый из них с соседом, для образования связей. A запутывается с B, C – с D и так далее. Так получается сеть более высокого уровня. Затем запутайте AB с CD, а EF с GH, чтобы подняться ещё на один уровень сети. И, наконец, ABCD запутывается с EFGH для формирования самого высокого уровня. «В каком-то смысле можно сказать, что запутанность используется для построения волновой функции многих тел»,- писал в прошлом году в своей работе Роман Орус [Román Orús], физик из Университета им. Иоганна Гутенберга (Германия).
Почему же некоторые физики так оптимистично оценивают потенциал тензорных сетей – особенно MERA – способный привести их к квантовой гравитации? Поскольку сети показывают, как простая геометрическая структура может появиться из сложных взаимодействий между многими объектами. И Свингл с единомышленниками надеется, что эту новую геометрию удастся использовать, показав, как она объясняет механизм превращения отдельных кусочков квантовой информации в плавное, непрерывное пространство-время.
Границы пространства-времени
Специалисты по физике конденсированных сред при разработке тензорных сетей нечаянно обнаружили дополнительное измерение: эта техника приводит к появлению двумерных систем в одном измерении. А специалисты по теории гравитации убирали одно измерение – переходя от трёх к двум – разрабатывая т.н. голографический принцип. Две этих концепции могут объединиться и создать более сложное представление о пространстве-времени.
В 1970-х физик Джейкоб Бекенштейн [Jacob Bekenstein] показал, что информация о внутренности чёрной дыры закодирована на её плоской двумерной поверхности (на границе), а не в её трёхмерном объёме. Через двадцать лет Леонард Сасскинд и Герард ’т Хоофт [Leonard Susskind and Gerard ’t Hooft] расширили это понятие до всей Вселенной, приравняв её к голограмме: наша трёхмерная Вселенная во всём её великолепии возникает из двумерного «исходного кода». В 1997 Хуан Малдасена [Juan Maldacena] нашёл конкретный пример работы голограммы, продемонстрировав, что игрушечная модель описания плоского пространства без гравитации эквивалентна описанию седловидного пространства с гравитацией. Эту взаимосвязь физики называют «дуальностью».
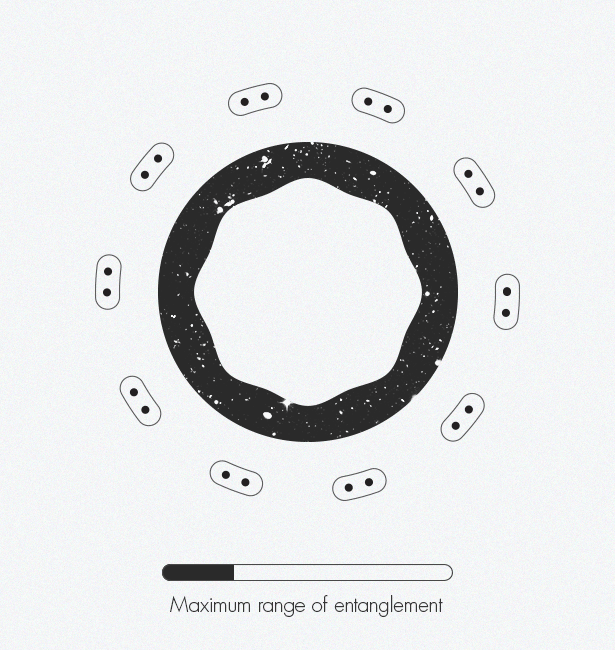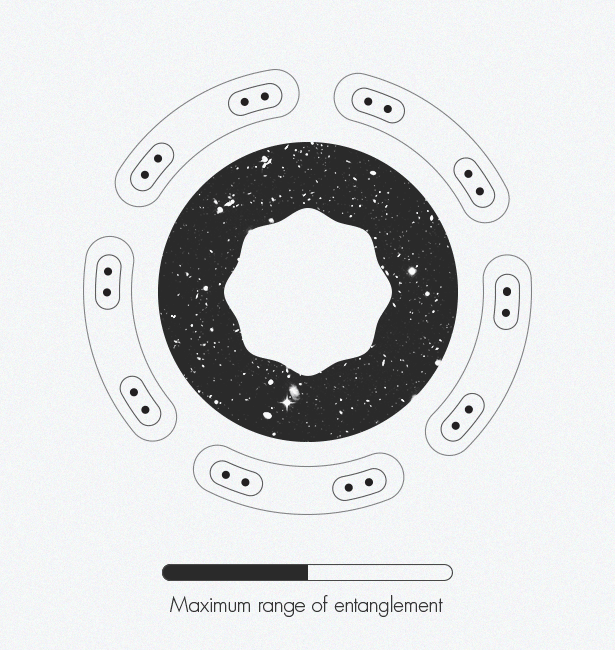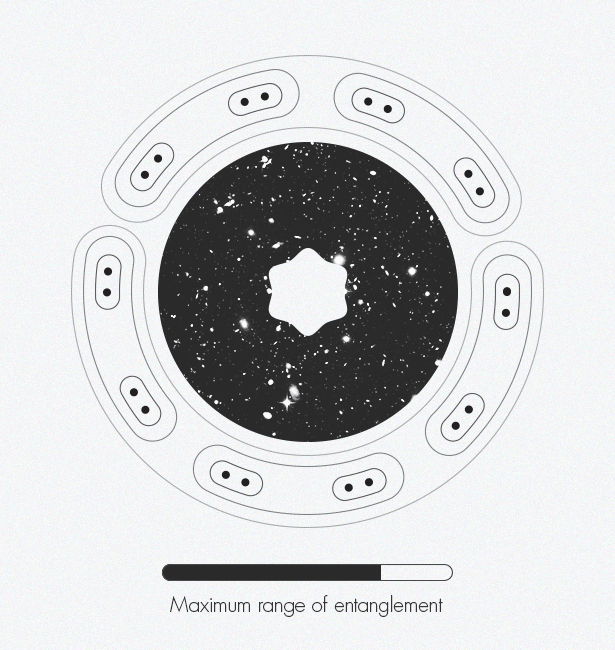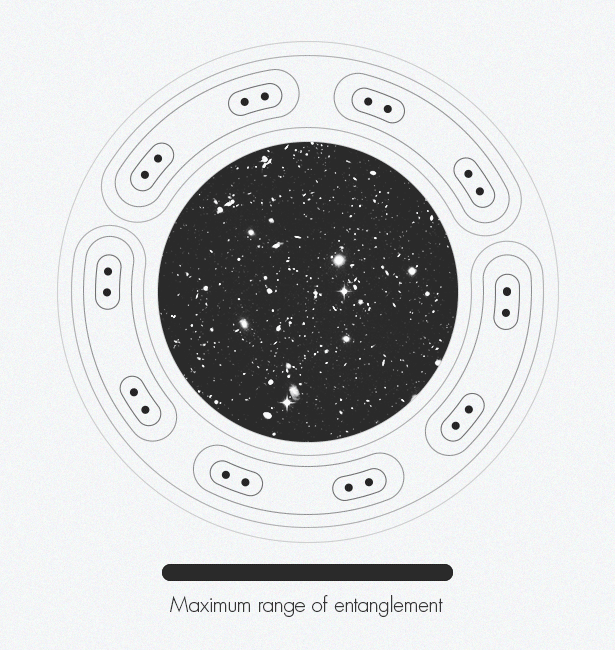
Марк ван Раамсдонк [Mark Van Raamsdonk] представляет, как запутанность постепенно создаёт пространство-время. По краям фигуры отдельные частицы-точки начинают запутываться друг с другом. Эти запутанные пары запутываются с другими парами. По мере запутывания всё большего количества пар появляется структура пространства-времени.
Марк ван Раамсдонк, специалист по теории струн из Университета Британской Колумбии (Ванкувер), сравнивает этот голографический принцип с двумерным компьютерным чипом, содержащим код для создания трёхмерного виртуального мира в компьютерной игре. Мы живём внутри трёхмерного пространства игры. В каком-то смысле наше пространство иллюзорно и является лишь эфемерным изображением, висящим в воздухе. Но ван Раамсдонк подчёркивает, что «в компьютере всё-таки есть некая физическая сущность, хранящая всю информацию».
Идея получила широкое признание среди физиков-теоретиков, но они всё ещё сражаются с тем, как именно меньшие измерения хранят информацию о геометрии пространства-времени. Загвоздка в том, что наш метафорический компьютерный чип должен быть неким квантовым компьютером, в котором привычные нолики и единички заменены кубитами, способными одновременно представлять все возможные состояния от нуля до единицы. Эти кубиты должны быть запутаны – так, чтобы состояние одного кубита было определено состоянием его соседа – до того, как можно будет закодировать реалистичный трёхмерный мир.
Точно также запутанность выглядит фундаментальной особенностью пространства-времени. К этому выводу пришло двое учёных в 2006-м: Шинсей Рю [Shinsei Ryu] (Иллинойский университет) и Тадаши Такаянаги [Tadashi Takayanagi] (Киотский университет), поделившие в 2015 году премию «Новые горизонты физики». «Идея в том, что то, как кодируется геометрия пространства-времени, сильно связана с тем, как разные части этого чипа запутаны друг с другом»,- поясняет ван Раамсдонк.
Вдохновлённых их работой, а также последовавшей за ней работой Малдасены, в 2010-м году ван Раамсдонк предложил мысленный эксперимент, демонстрирующий критическую роль запутанности в формировании пространства-времени. Он исследовал, что случится, если поделить компьютерный чип пополам, а затем удалить запутанность между кубитами в двух половинках. Он обнаружил, что пространство-время начинает разрушаться так же, как растягивание кусочка жвачки за концы приводит к появлению разрыва в середине. Разделение этого чипа на всё более мелкие кусочки разрывает пространство время до тех пор, пока не остаются лишь отдельные, не связанные друг с другом кусочки. «Если убрать запутанность, пространство-время просто разваливается»,- говорит ван Раамсдонк. Точно так же, «если вы хотите построить пространство-время, вам придётся запутывать кубиты определённым образом».
Сложите эти мысли с работой Свингла, связывающей запутанную структуру пространства-времени и голографический принцип с тензорными сетями и ещё один кусочек головоломки встаёт на место. Искривлённое пространство-время естественным образом возникает из запутанности в тензорных сетях посредством голографии. «Пространство-время – это геометрическое представление этой квантовой информации»,- говорит ван Раамсдонк.
И как же выглядит эта геометрия? В случае седловидного пространства-времени Малдасены, она выглядит, как один из рисунков «предел – круг» Эшера из 1950-1960-х годов. Эшер долго интересовался порядком и симметрией, включая эти математические концепции в свои работы с 1936 года, когда он посетил архитектурно-парковый ансамбль Альгамбра в Испании и нашёл вдохновение в тамошних повторяющихся плиточных узорах, типичных для мавританской архитектуры, известных, как мозаика.
Его гравюры на дереве «предел – круг» иллюстрируют гиперболические геометрии: искажение пространства с отрицательной кривизной на двумерной поверхности диска напоминает уплощение глобуса до двумерной карты Земли, искажающее форму континентов. К примеру, "предел – круг IV" (ад и рай) выглядит, как множество повторяющихся фигурок ангелов и демонов. В гиперболическом пространстве размер всех фигур был бы одинаковым, но в двумерных представлениях Эшера фигурки у края выглядят меньше, чем в центре. Диаграмма тензорной сети очень сильно напоминает серию «предел – круг», визуальное представление глубоких связей, найденных Свинглом при посещении тех самых занятий по теории струн.
На сегодняшний день тензорный анализ ограничен моделированием пространства-времени (как у Малдасены), не описывающим ту Вселенную, в которой живём мы – она не имеет форму седла, а её расширение ускоряется. Физики могут переводить между моделями только в отдельных, особых случаях. В идеале им требуется универсальный «словарь». И им хотелось бы выводить этот словарь напрямую, не пользуясь приближениями. «С этими дуальностями мы оказались в забавном положении, потому чт�� все соглашаются, что они очень важны, но никто не знает, как их выводить»,- говорит Прескилл. «Может, подход тензорных сетей сделает возможным дальнейшее продвижение. Думаю, признаком прогресса было бы, если бы мы могли сказать, пусть даже в случае игрушечной модели: 'Ага! Вот он, вывод словаря!'. Это был бы серьёзный намёк на то, что мы наткнулись на что-то важное».
За последний год Свингл и ван Раамсдонк работали вместе, чтобы продвинуть свои работы в область, выходящую из статичного представления пространства-времени в динамическое. Их интересует, как пространство-время изменяется со временем и как оно изгибается в ответ на эти изменения. Пока что им удалось вывести уравнения Эйнштейна, конкретно – принцип эквивалентности. Это доказывает, что динамика пространства-времени, как и его геометрия, основана на запутанных кубитах. Начало многообещающее.
«Вопрос 'Что такое пространство-время?' кажется абсолютно философским,- говорит ван Раамсдонк. – На самом деле найти на него ответ, конкретный и позволяющий вести расчёты пространства-времени – это было бы потрясающе».