При обсуждении строения атома и вещества часто можно прочитать, что вещество на 99.99…% состоит из пустоты, с разными версиями количества девяток. Как мы сейчас увидим, это утверждение имеет весьма шаткие основания, а попытки оценить долю пустоты в веществе могут с одинаковым успехом дать любое число от 0 до 100%. Последовательное же рассмотрение вопроса в рамках квантовой механики показывает, что от пустоты вещество отличается довольно сильно.

Что не так с 99%?


Традиционная линия рассуждений(*) выглядит так: в атоме, имеющем размер около одного ангстрема (10–10 метра), электроны вращаются вокруг ядра, размер которого в 100 000 раз меньше (около 10–15 метра). Размер самого электрона равен нулю, это точечная частица(**), поэтому атом оказывается практически пустым: в нем «непустое» лишь ядро. Чтобы получить долю объема атома, занимаемого ядром, нужно возвести в куб отношение их размеров. Получаем, что ядро занимает 10–15 объема атома, остальную долю объема — это 99.99…% с 13 девятками после запятой — занимает пустота.


Если атом растянуть до размеров футбольного поля, то ядро будет величиной с маковое зернышко.

Что не так в этих рассуждениях? Давайте продолжим ту же логику, рассматривая уже не атом, а его ядро. Мы считали атомное ядро непустым, но ведь оно состоит из протонов и нейтронов, которые, в свою очередь, состоят из фундаментальных частиц — кварков и глюонов(***). По современным представлениям, кварки и глюоны тоже являются точечными частицами, как и электрон. Следуя такой же линии рассуждений, как и в случае атома, получим, что ядро — тоже пустота, в которой летают частицы нулевых размеров. Итог: вещество ровно на 100% состоит из пустоты. Эта линия рассуждений завела нас в никуда.



Что говорит квантовая механика?


Квантовая механика говорит нам, что электрон в атоме является не маленьким шариком, летающим по орбите вокруг ядра, а размазан по пространству в виде вероятностного облака, называемого орбиталью. Плотность этого облака, или просто электронная плотность $n(\vec{r})$, зависит от координаты $\vec{r}$. Эта зависимость своя для каждой орбитали, тем не менее, есть общая закономерность: $n(\vec{r})$ заметно отлична от нуля в области пространства размерами порядка ангстрема, а на больших расстояниях от ядра экспоненциально убывает.


Типичное поведение электронной плотности в атоме для разных электронных орбиталей. Источник.

Отсюда берется характерный размер атома в один ангстрем, использованный выше при сравнении размеров атома и ядра. Какой же количественный ответ на вопрос о доле пустоты в веществе может дать нам квантовая механика? Для этого нужно оценить суммарный объем, занимаемый электронными орбиталями всех атомов. А для этого, в свою очередь, следует провести четкую границу между атомом и окружающей его пустотой. Но как это сделать? Формально электронная плотность $n(\vec{r})$, хоть и стремится к нулю при удалении от ядра, никогда в ноль не обращается, поэтому каждая атомная орбиталь заполняет если не всю Вселенную, то, как минимум, весь объем рассматриваемого куска вещества. В этом случае получается, что пустоты в веществе нет — в любой точке есть отличная от нуля вероятность найти электрон.

Можно определить границу атома как место, где электронная плотность достигает 1/2 от максимальной. Или 1/15 — такая граница будет отстоять дальше от ядра. Или как поверхность, внутри которой содержится 1/2 всей суммарной электронной плотности. Можно ухватить и больше объема, проведя поверхность, внутрь которой попадает, например, 9/10 всей плотности.


Плотность электронного облака для орбитали $3p_{m=0}$ в атоме водорода (показана белым цветом) и разные варианты проведения условной границы атома.

Как видим, по-разному проводя условные границы атомов, можно получать разные величины занимаемого ими объема. Поэтому и для доли пустоты в веществе можно получить любой ответ от 0 до 100%. Например, в этом видео доля пустоты оценивается как 90%. Почему именно 90, а не 80 или 95? Видимо, автор взял какой-то «стандартный» размер атома в районе одного ангстрема.

Хотя для точного определения границ атома поверхности равной электронной плотности и не годятся, они удобны, когда нужно наглядно изобразить структуру вещества на микроуровне. По форме этих поверхностей можно судить о структуре молекулярных орбиталей и химических связей.


Пример поверхности (она зеленая и полупрозрачная), на которой электронная плотность в кристалле принимает постоянное значение. Источник.


А так выглядят поверхности постоянной плотности в некоторых белках. Источник.

Что говорит квантовая теория поля?


Даже если вещество от пустоты нельзя четко отделить, можно ли хотя бы ответить на вопрос, чем вообще, с точки зрения квантовой теории, вещество отличается от пустого пространства? Для ответа обратимся к квантовой теории поля, изучающей системы многих частиц и вакуум. В этой теории любое состояние системы (точнее, квантованного поля), в которой может находиться 0, 1, 2 и т.д. частиц, характеризуется вектором, длина которого равна единице.

Подробнее
Каждый вектор $\vec{a}$ можно задать его проекциями $a_1,\,a_2,\,\ldots$ на координатные оси, число которых равно размерности пространства $D$: $\vec{a}=\{a_1,a_2,\ldots,a_D\}$. Квантовые системы описываются векторами в бесконечномерном пространстве, то есть такими векторами, число проекций которого бесконечно: $\vec{a}=\{a_1,a_2,\ldots\}$. Сами же проекции $a_1,\,a_2,\,\ldots$ в квантовой механике являются комплексными числами, это обстоятельство важно при описании явлений интерференции.

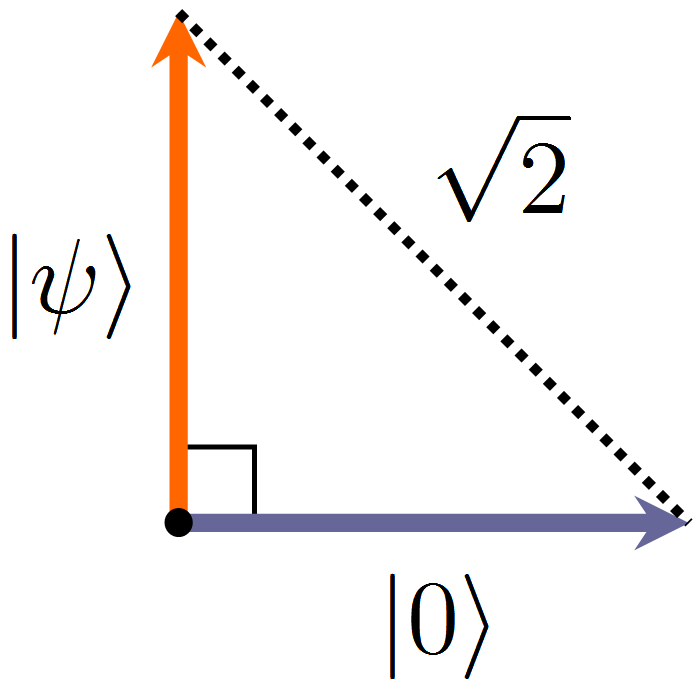
Если в системе нет ни одной частицы (пустота), ее состояние называют вакуумом, и соответствующий вектор принято обозначать как $|0\rangle$. Атом с одним электроном на любой орбитали — это состояние системы с одной частицей, вектор которого можно обозначить как $|\psi\rangle$. Насколько отличаются эти два состояния друг от друга? Существуют разные способы описания «расстояния» между векторами, наиболее простой и часто используемый(****) — посчитать длину разности векторов $|\psi\rangle-|0\rangle$. Можно показать, что векторы $|0\rangle$ и $|\psi\rangle$ взаимно перпендикулярны, это обычная ситуация для существенно отличающихся друг от друга квантовых состояний. Выходит, что, с точки зрения квантовой теории поля, «расстояние» между пустотой и электроном, находящимся на атомной орбитали, равно $\sqrt{2}$.


Два взаимно перпендикулярных вектора состояния — вакуум и один электрон на атомной орбитали, — и расстояние между ними.

Получаемый ответ — что вещество всегда радикально отличается от пустоты, даже если содержит одну частицу на кубический километр, — не очень удовлетворителен, потому что из него начисто выпадает распределение вещества в пространстве. Можно ли ввести меру отличия вещества от пустоты, показывающую, насколько сильно они отличаются не в целом, а локально, в каждой точке $\vec{r}$? Да, такую меру найти можно, и ей является не что иное как электронная плотность $n(\vec{r})$. Там, где электронная плотность спадает до предельно малых значений, отличие вещества от пустоты также становится несущественным.

Пара формул
Это можно понять, если учесть, что квадрат расстояния $||\psi-0||^2$ представляется в виде:

$||\psi-0||^2=\langle0|0\rangle+\langle\psi|\psi\rangle=1+\int|\Psi(\vec{r}_1\ldots\vec{r}_N)|^2\:d\vec{r}_1\ldots d\vec{r}_N=1+\frac1N\int n(\vec{r})\:d\vec{r},$


где $\Psi(\vec{r}_1\ldots\vec{r}_N)$ — волновая функция многоэлектронной системы, $N$ — число электронов. Как видим, квадрат расстояния складывается из двух частей: одна из них равна единице, другая набегает за счет интеграла от электронной плотности по пространству.



Линии равных электронных плотностей в кристалле Na2GeS3. Чем дальше от атомных ядер, тем ниже плотность, и тем ближе пустота. Источник.

Итак, мы видим, что:

  • Если рассуждать в духе «в атоме непустым является лишь ядро», то придется признать, что вещество — ровно на 100% пустота, потому что ядро — это такой же пустой «атом», только состоящий из других частиц.
  • В квантовой механике электронные оболочки атомов размазаны в пространстве, и невозможно точно сказать, где кончается атом и начинается окружающее его пустое пространство. Как следствие, нельзя и точно сказать, какова доля пустоты в веществе — с одинаковым успехом можно взять любое число от 0 до 100%.
  • С точки зрения квантовой теории поля, вещество даже с одним электроном существенно отличается от вакуума — эти два квантовых состояния представляются взаимно перпендикулярными векторами, расстояние между которыми равно $\sqrt{2}$.
  • Однако можно, в каком-то смысле, ввести меру отличия вещества от вакуума не в целом, а локально, в каждой точке пространства. Этой мерой является электронная плотность $n(\vec{r})$. К сожалению, электронная плотность — размерная величина, она имеет размерность м–3, и поэтому не дает нам ответа на вопрос «на сколько процентов вещество вот в этой точке отличается от пустоты». С ее помощью можно лишь судить о том, где вещество сильнее отличается от пустоты, а где слабее. Вблизи центров атомов $n(\vec{r})$ максимальна, там вещество отличается от пустоты сильнее всего, а на больших расстояниях от атомов она очень быстро убывает, и отличие вещества от пустоты становится несущественным.


(*)Вот примеры такого рода рассуждений, в которых, впрочем, соотношение размеров атома и ядра иногда преувеличивают в миллионы раз:
• www.popmech.ru/science/10566-zhizn-v-pustote-kvantovoe-osoznanie
• www.yaplakal.com/forum7/topic1503279.html
• pikabu.ru/story/tyi_nichto_561687
• thequestion.ru/questions/10102/atom-sostoit-iz-pustoty-vsyo-materialnoe-sostoit-iz-atomov-kak-materialnoe-mozhet-sostoyat-iz-pustoty

(**)По крайней мере, эксперименты на Большом электрон-позитронном коллайдере показали, что размер электрона не превышает 10–19 м. Более поздние сверхточные измерения м��гнитного момента электрона дали верхнюю оценку размера электрона, равную 10–20 м. Эти оценки показывают, что электрон, как минимум, в десятки тысяч раз меньше ядра.

(***)Интересный факт: три кварка, из которых состоит протон, дают лишь менее 2% его массы. Остальная часть массы — это виртуальные частицы (кварки и глюоны), возникающие в результате взаимодействия трех исходных кварков. Этих частиц так много, что они образуют целое «море», и поэтому называются «морскими» кварками и глюонами.

(****)В случае двух чистых квантовых состояний $|0\rangle$ и $|\psi\rangle$ такие меры расстояния между ними, как метрика Гильберта-Шмидта и метрика Фубини-Штуди, сводятся именно к длине вектора $|\psi\rangle-|0\rangle$.