В данной статье рассматриваются различные методы приближений иррациональных чисел, а также попутно затрагиваются вопросы, косвенно связанные с этой темой
В сборнике Арнольда есть следующая задача
38. Вычислить сумму:

(с ошибкой не более 1% от ответа)
Ниже представлен алгоритм для вычисления частичных сумм этого ряда на языке Scheme (Lisp) в обыкновенных дробях
Два последних примера drRacket вычислил с ошибкой

Можно заметить, что частичная сумма первых слагаемых
слагаемых 
Доказательство по индукции
1. При гипотеза верна, так как
гипотеза верна, так как 
2. Предположим, что гипотеза верна и для , т.е. что
, т.е. что
где — некоторое натуральное число
— некоторое натуральное число
Установим справедливость и при
Доказательство методом перебора
Пусть дана последовательность
Предположим, что частичная сумма первых слагаемых
слагаемых 
Тогда
Отсюда


 и так далее
и так далее
Пятясь назад, придём к
Теорема Вейерштрасса гласит
данная последовательность возрастает, поскольку
данная последовательность ограничена сверху, поскольку

отобразим целочисленные координаты оси на график функции
на график функции

отобразим полученные точки на график функции
получим систему вложенных отрезков с неподвижной точкой
![$ [A,B]\supset[A,C]\supset [A,D]\supset [A,E]\supset [A,F]\supset... $](https://habrastorage.org/getpro/habr//formulas/3e2/fdf/a0a/3e2fdfa0ae3508ce40dd0bfa0569b8b6.svg)

Кстати, данные частичные суммы являются египетскими дробями, а непосредственно сами слагаемые
являются египетскими дробями, а непосредственно сами слагаемые  являются аликвотными дробями
являются аликвотными дробями
Другим представлением египетской дроби является сумма
 ,
,
где
А также сумма

где
(«Квант» 1970)
В следующей задаче требуется найти НОД двух соседних чисел Фибоначчи
43.Числа кроликов («Фибоначчи»), образуют последовательность в которой
в которой  для всякого
для всякого  . Найти наибольший общий делитель чисел
. Найти наибольший общий делитель чисел  и
и  .
.
Для решения данной задачи достаточно доказать, что два соседних числа Фибоначчи взаимно просты, то есть доказать справедливость тождества
Доказательство из книги «За страницами учебника математики» [10-11]
Добавлю, что
 по алгоритму Евклида
по алгоритму Евклида

где — остаток от деления
— остаток от деления  на
на 
и в данном конкретном случае поскольку
поскольку 
Доказательство из книги «Числа Фибоначчи» Н. Н. Воробьёва
Похожий метод, метод перебора последовательности можно применить для доказательства тождества Кассини, которое выражается соотношением:
можно применить для доказательства тождества Кассини, которое выражается соотношением:

Предположим, что

Перебрав последовательность в обратном направлении, придём к тому, что левая и правая части данного равенства обе тождественны единице
Домножим тождество на
на  :
:

Вычтем :
:





Данное выражение показывает, что некая величина, которой тождественны левая и правая части равенства, меняет свой знак на противоположный при переходе






и т.д.
В следующей задаче необходимо вычислить золотое сечение, . [Это соотношение сторон открытки, остающейся себе подобной при отрезании квадрата, стороной которого является меньшая сторона открытки.]
. [Это соотношение сторон открытки, остающейся себе подобной при отрезании квадрата, стороной которого является меньшая сторона открытки.]
53. Для последовательности чисел Фибоначчи задачи 43 найти предел отношения
задачи 43 найти предел отношения  при стремлении
при стремлении  к бесконечности:
к бесконечности:
Отметим на числовой оси отрезки

Числа с чётными номерами представляют растущую последовательность
с чётными номерами представляют растущую последовательность
Числа с нечётными номерами представляют убывающую последовательность
с нечётными номерами представляют убывающую последовательность
По лемме о вложенных промежутках (Курс дифференциального и интегрального исчисления, 38)
А значит
Разделив на
на  , получим уравнение
, получим уравнение 
После замены


получится квадратное уравнение , положительным решением которого является золотое сечение
, положительным решением которого является золотое сечение
Различные методы решения этого уравнения приводятся ниже, в отдельном разделе, посвящённом решению квадратных уравнений
Если в программе geogebra соединить дугами о��ружности точки 2 и ,
,  и
и  ,
,  и
и  и т.д. — получим самоподобную фигуру
и т.д. — получим самоподобную фигуру

Для сравнения

Кстати, в правильной пятиконечной звезде (звёздчатом пятиугольнике) каждый отрезок делится другим отрезком, пересекающим его, в золотом сечении

В правильном пятиугольнике отношение диагонали к стороне также равно
Вообще, существует стандартный алгоритм вычисления чисел Фибоначчи на Python
(алгоритм представлен на сайте Python.org)
Приближения к являются отношением суммы двух соседних чисел
являются отношением суммы двух соседних чисел  и
и  к числу
к числу 
На двенадцатом шаге получим приближение 1.61805
Формула Бине использует для вычисления
для вычисления  -ого числа Фибоначчи
-ого числа Фибоначчи

Пусть
Тогда выражения вида будут принадлежать множеству
будут принадлежать множеству
 поскольку
поскольку

то есть
Приняв
получим приближение


Алгоритм вычисления
n=10 Fn=88.99775275224582
Если в уравнении в правой части заменить x на
в правой части заменить x на  получим
получим 
Продолжая производить замены, придём к представлению золотого сечения в виде цепной дроби
Задача из учебника SICP
Упражнение 1.35.
Покажите, что золотое сечение (раздел 1.2.2) есть неподвижная точка трансформации
(раздел 1.2.2) есть неподвижная точка трансформации  , и используйте этот факт для вычисления
, и используйте этот факт для вычисления  с помощью процедуры fixed-point.
с помощью процедуры fixed-point.
пример вычисления факториала
Алгоритм решения задачи 1.35
Сперва опишем счётчик, инкрементирующий переменную в цикле
в цикле
Оператор set! позволяет переопределить значение глобальной переменной
Определим глобальную переменную fixed-point и будем переопределять значение данной переменной в цикле do c помощью оператора set!
Задачник Арнольда
54. Вычислить бесконечную цепную дробь
Решение
Рассмотрим уравнение
Согласно теоремам 236 и 235 из книги «Теория чисел»:
Составляем таблицу значений и
и  при
при 
так что
и поскольку то
то
Пусть дана последовательность
 образованная умножением подкоренного выражения на радикал
образованная умножением подкоренного выражения на радикал 
Для этой последовательности справедливо равенство

Далее надо доказать само существование предела
поскольку, если этот предел существует, то он должен равняться числу
Здесь показатели степеней представляют геометрическую прогрессию, то есть

При перемножении степеней с одинаковыми основаниями показатели степеней складываются
Сумма геометрической прогрессии
На рисунке ниже является неподвижной точкой системы вложенных отрезков, высекаемых графиками функций
является неподвижной точкой системы вложенных отрезков, высекаемых графиками функций  на прямой
на прямой  (а также системы, высекаемой на прямой
(а также системы, высекаемой на прямой  )
)

Если уравнение переписать в виде
переписать в виде  то заменяя
то заменяя  под корнем на
под корнем на  получим
получим 
Тогда

Данное выражение является частным случаем варианты
Курс дифференциального и интегрального исчисления, 35 (2)
То есть является одним из бесконечного множества пределов: корней уравнения
является одним из бесконечного множества пределов: корней уравнения  при различных
при различных 
Далее в «Курсе дифференциального и интегрального исчисления», 35(3) рассматривается алгоритм вычисления обратного числа (такого числа 1/с, произведение которого на данное число с равно единице)
Функция reciprocal принимает на вход число , начальное значение
, начальное значение  , количество итераций
, количество итераций  и возвращает массив приближений к числу
и возвращает массив приближений к числу  .
.
 при
при 
 при
при 
 при
при 
и т.д.
Примеры работы функции reciprocal при подстановке в переменную чисел 3,5 и 8
чисел 3,5 и 8
Геометрическое представление о данном алгоритме даёт метод Ньютона или метод касательных
Пусть дано уравнение прямой
Уравнение прямой, проходящей через точку
Тогда
Так как угловой коэффициент касательной к графику дифференцируемой функции в точке с абсциссой равен
равен  , то уравнение касательной имеет вид
, то уравнение касательной имеет вид
Производной функции называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  :
:
Для гиперболы
Знаменатель состоит из двух слагаемых, второе при малых значениях пренебрежимо мало по сравнению с первым, значит
пренебрежимо мало по сравнению с первым, значит
Касательными к гиперболе
к гиперболе  являются функции
являются функции
 , то есть
, то есть

Подставляя числа вместо
вместо  получим уравнения касательных
получим уравнения касательных
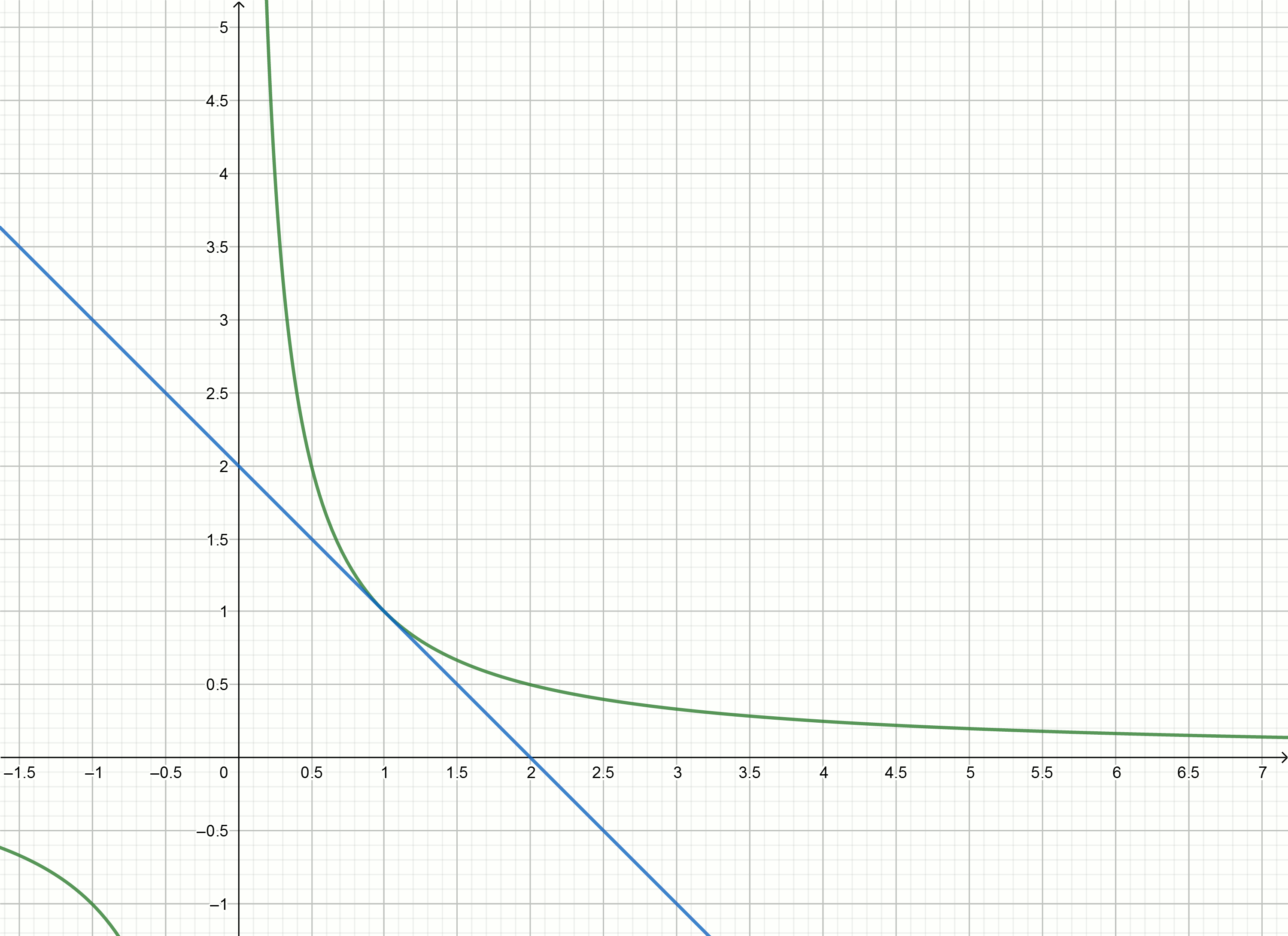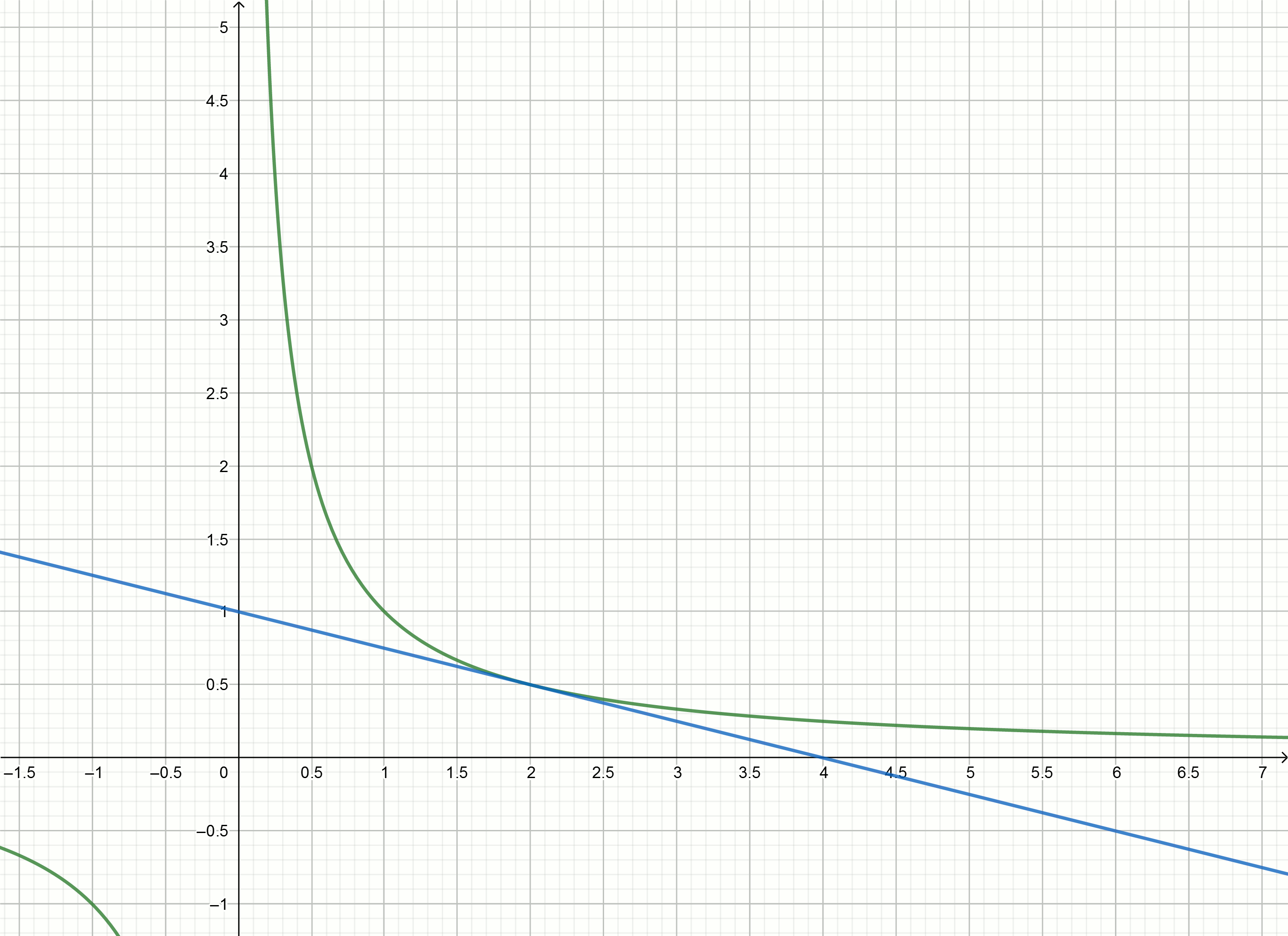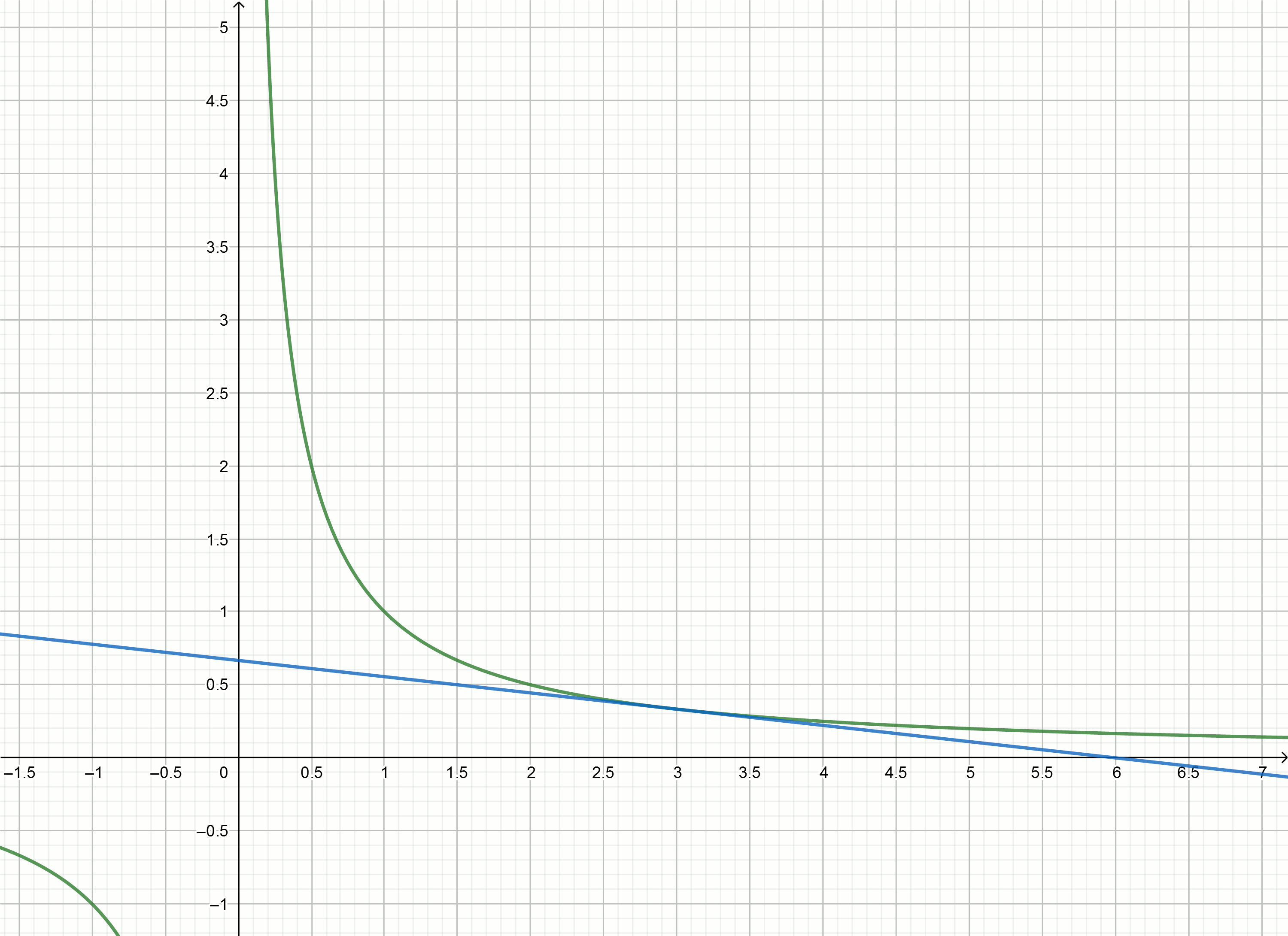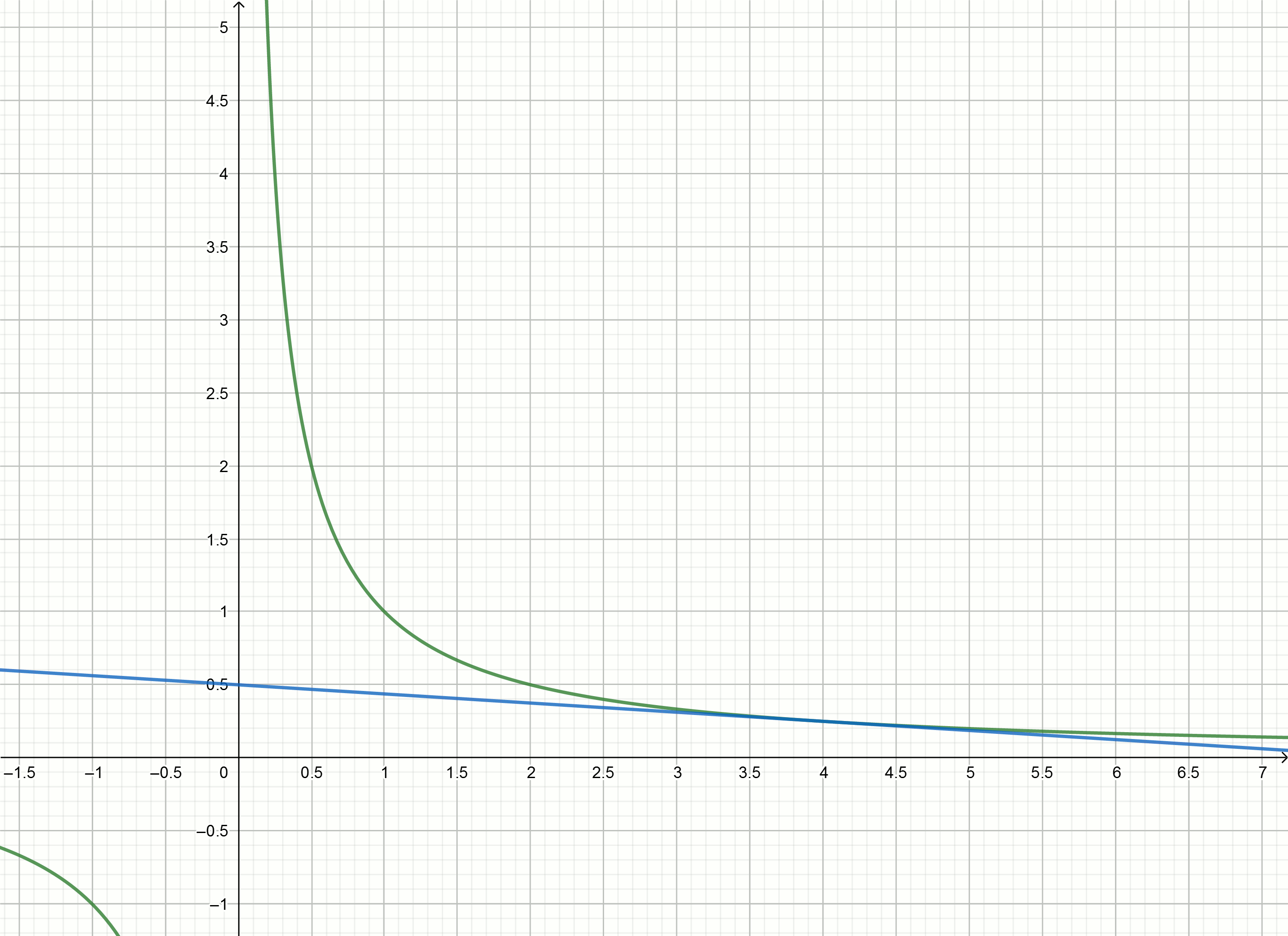
Если сдвинуть гиперболу вниз на , то она пересечёт ось абсцисс в точке
, то она пересечёт ось абсцисс в точке 
Уравнение касательных преобразуется в
Далее, приравняв уравнение касательной к нулю и выразив , получим уравнение
, получим уравнение 
Вместо подставим
подставим 
Вместо подставим
подставим 
Получим выражение
Раскрыв скобки, получим
Подставим в уравнение
в уравнение  и посмотрим, какие значения будет принимать
и посмотрим, какие значения будет принимать  по мере приближения к
по мере приближения к 
Пусть
Тогда округлённая обратная величина будет равна
Подставим эти значения в уравнение
Касательные
с каждой новой итерацией будут всё ближе к искомой величине
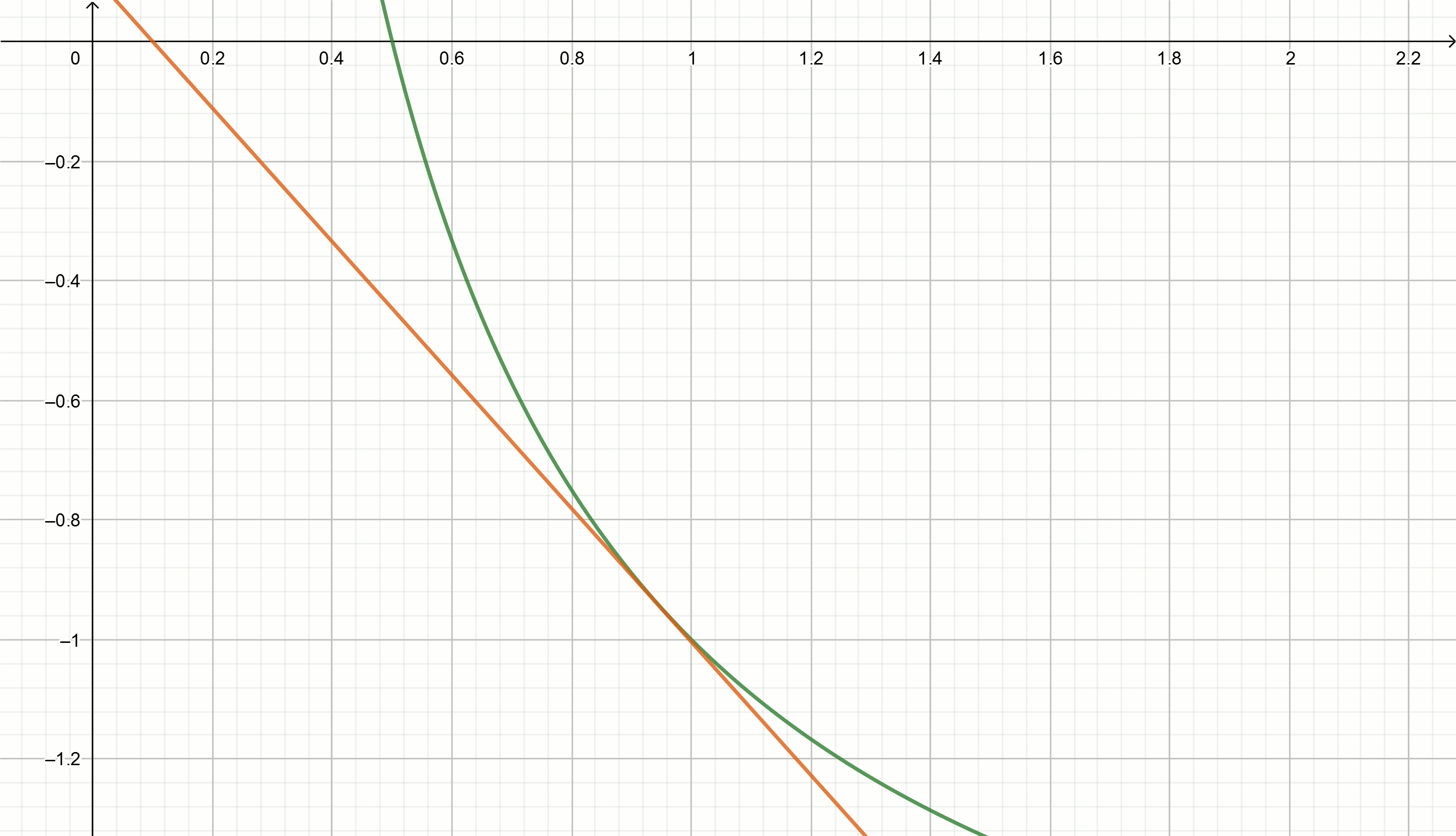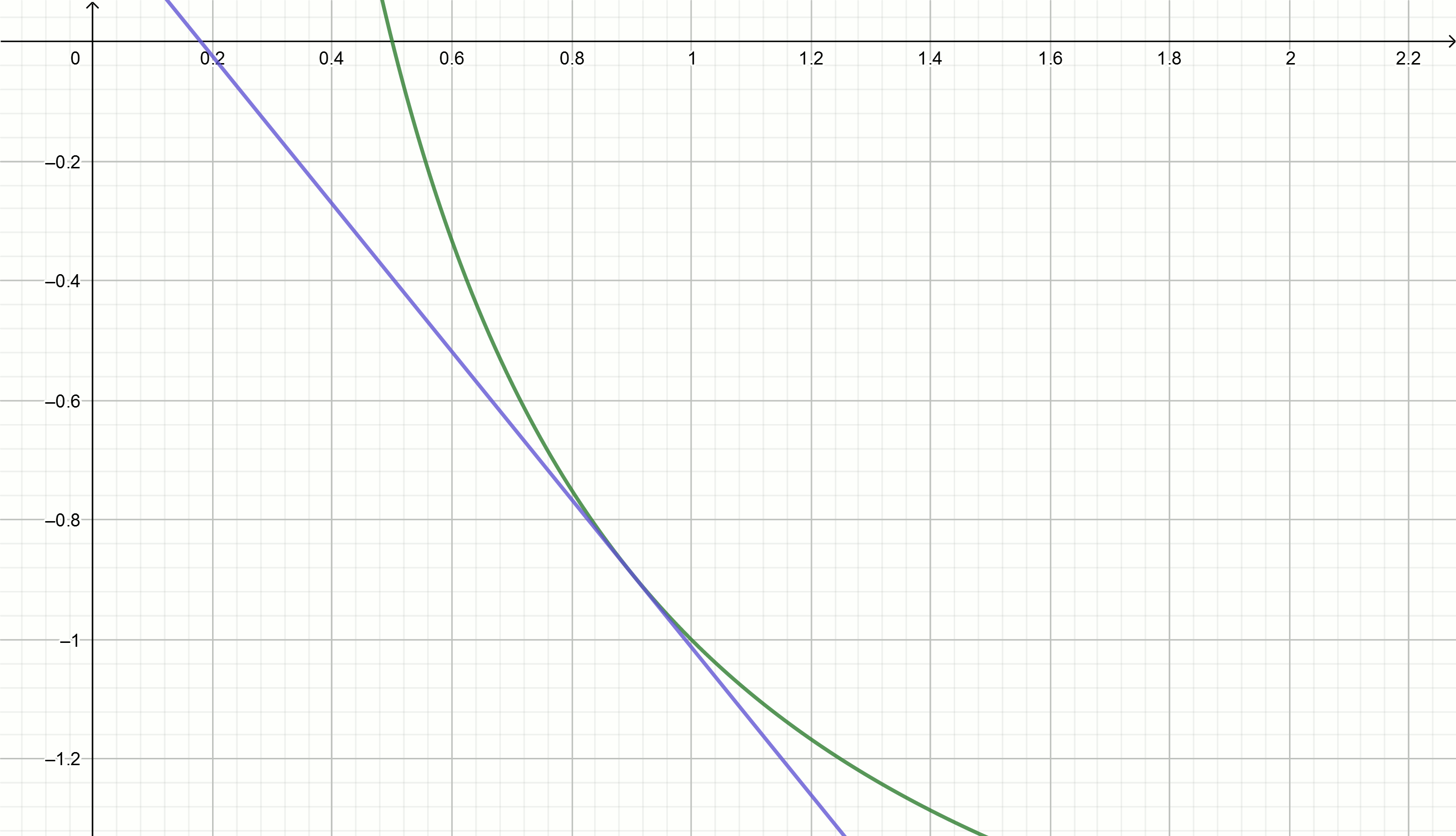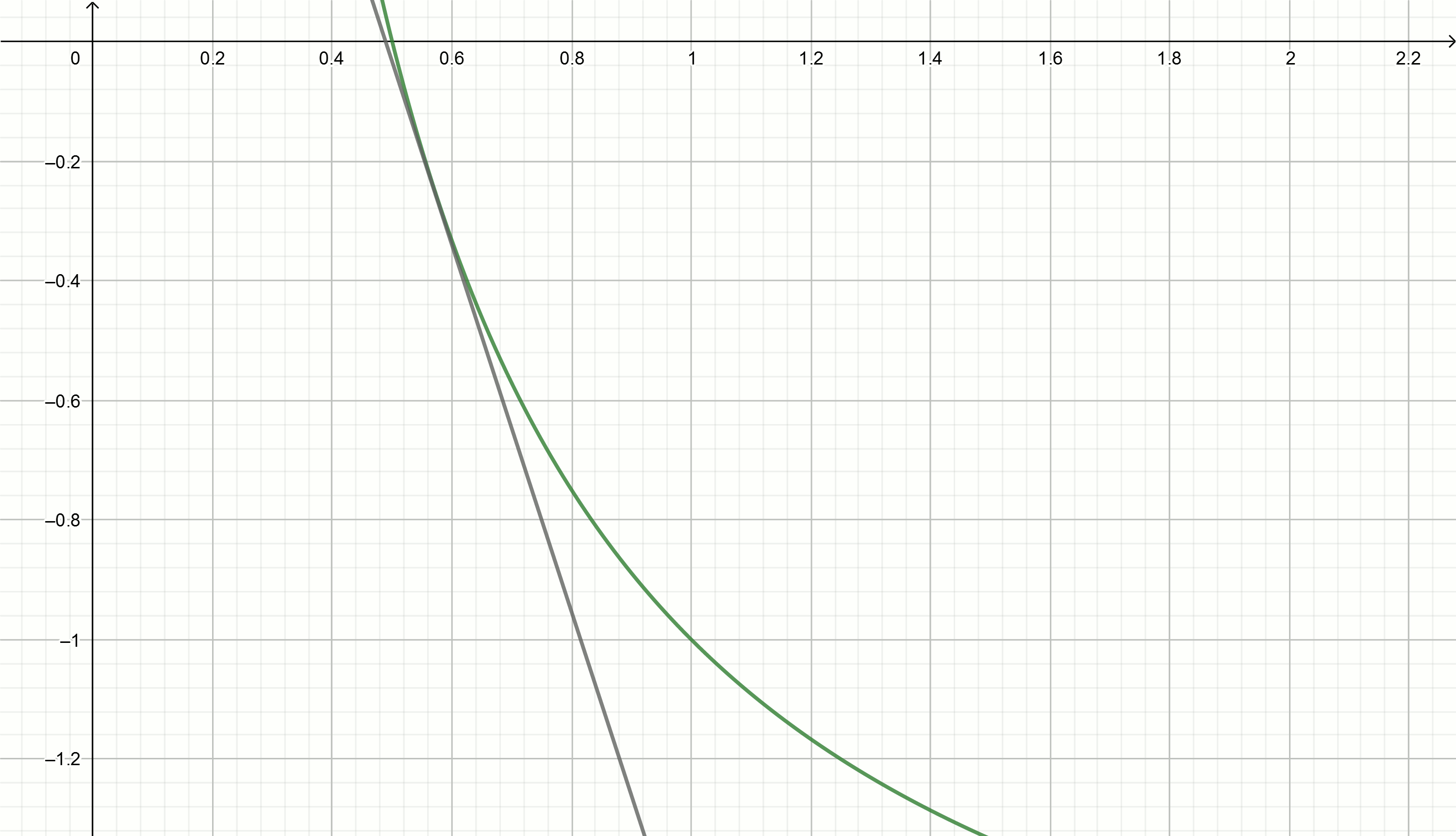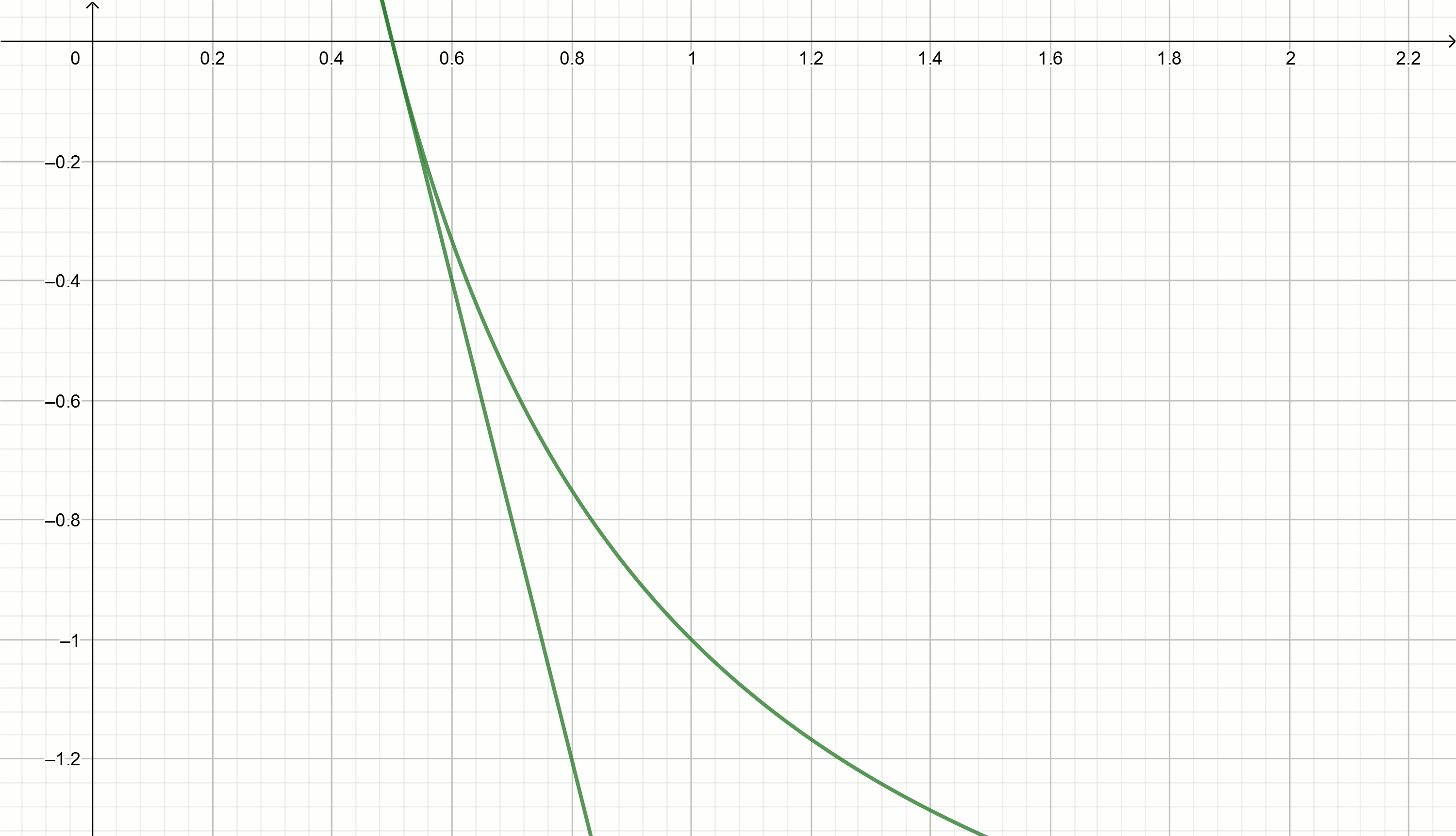
Итерационный метод Герона для извлечения квадратного корня из числа использует формулу
использует формулу

Пусть , тогда
, тогда 
Пусть равняется целой части
равняется целой части 
Проведём горизонтальную прямую через точку
Прямая пересечёт графики функции
пересечёт графики функции  и
и  в точках
в точках  и
и 
Пусть точка лежит на прямой
лежит на прямой 
… точка лежит на прямой
лежит на прямой 
… точка лежит на прямой
лежит на прямой 
Последовательность монотонна и ограничена, а значит сходится
монотонна и ограничена, а значит сходится

Проецируя эти приближения на ось получим систему вложенных отрезков
получим систему вложенных отрезков
![$ [x_{1},a/x_{1}] \supset [x_{2},a/x_{2}]\supset [x_{3},a/x_{3}]\supset...[x_{n},a/x_{n}]$](https://habrastorage.org/getpro/habr//formulas/83f/b8b/17f/83fb8b17f7ec6d7f0a8483869f852092.svg) с неподвижной точкой
с неподвижной точкой 
Слева от располагаются приближения по недостатку, справа приближения по избытку
располагаются приближения по недостатку, справа приближения по избытку
Формулу Герона можно получить из формулы общего вида

подставив в эту формулу числовое значение (натуральное число). В данном конкретном случае, поскольку необходимо вычислить корень квадратный, надо подставить число два.
В книге «Занимательная геометрия» сообщается другой старинный способ извлечения квадратного корня
Цитата:
Пусть надо вычислить . Он заключается между
. Он заключается между  и
и  и, следовательн��, равен
и, следовательн��, равен  с дробью, которую обозначим через
с дробью, которую обозначим через  .
.
Итак, , откуда
, откуда 
Квадрат дроби есть малая дробь, которую в первом приближении можно пренебречь, тогда имеем:
есть малая дробь, которую в первом приближении можно пренебречь, тогда имеем:
 , откуда
, откуда  и
и 
Значит, приближенно .
.
Если мы хотим определить значение корня ещё точнее, напишем уравнение
 , где
, где  -небольшая дробь, положительная или отрицательная.
-небольшая дробь, положительная или отрицательная.
Отсюда
 .
.
Отбросив , находим, что
, находим, что  приближенно равен
приближенно равен
 .
.
Следовательно, во втором приближении .
.
Третье приближение находим тем же приемом и т.д.
Вычисление квадратного корня с помощью цепных дробей использовал Рафаэль Бомбелли
Цитата:
Чтобы найти значение , сначала определим его целое приближение:
, сначала определим его целое приближение:  , где
, где 
Тогда . Отсюда несложно вывести, что
. Отсюда несложно вывести, что  . Повторно подставляя полученное выражение в формулу
. Повторно подставляя полученное выражение в формулу  , мы получаем разложение в цепную дробь:
, мы получаем разложение в цепную дробь:

следующий алгоритм использует разложение в цепную дробь
Способ выделения целой части позволяет представить иррациональное число в виде бесконечной цепной дроби с частыми числителями, равными единице
Вот пример разложения в цепную дробь числа из книги «Алгебра»
из книги «Алгебра»
Цитата:

Таким образом
Выделим целую часть числа . Значит,
. Значит,  можно представить в виде
можно представить в виде  . Ясно, что
. Ясно, что  , поэтому
, поэтому  . Снова уничтожим иррациональность в числителе второго слагаемого:
. Снова уничтожим иррациональность в числителе второго слагаемого:

В итоге получилось:

Проделаем еще один аналогичный шаг:

Нетрудно заметить, что процесс выделения целой части и образования цепной дроби в данном примере не имеет конца. В каждом новом знаменателе будет появляться и слагаемое
и слагаемое  . Поэтому ясно, что
. Поэтому ясно, что  представляется в виде бесконечной цепной дроби:
представляется в виде бесконечной цепной дроби:
![$ \sqrt{5} = [2, 4, 4, 4, ...] $](https://habrastorage.org/getpro/habr//formulas/a76/680/740/a76680740a64c74c6faf22f2547e5c9a.svg)
Гипотеза
Если , то цепная дробь числа
, то цепная дробь числа ![$ \sqrt{d} + [\sqrt{d}] $](https://habrastorage.org/getpro/habr//formulas/a2b/5ee/12a/a2b5ee12a04be4588ad45a0d66a0ad8a.svg) чисто периодическая.
чисто периодическая.
Эта гипотеза представлена в трудах Эвариста Галуа
Так чисто периодическая дробь![$ [2,2,2,...]$](https://habrastorage.org/getpro/habr//formulas/49d/3f5/d75/49d3f5d7542e4add30e52fc5582ae5ef.svg) является суммой непериодической части дроби
является суммой непериодической части дроби ![$[1;2,2,2,...] = \sqrt{2}$](https://habrastorage.org/getpro/habr//formulas/dfa/c7f/732/dfac7f73293323aadc5e605bd415196b.svg) и целой части
и целой части ![$ [\sqrt{2}] =1 $](https://habrastorage.org/getpro/habr//formulas/e84/9ce/4a2/e849ce4a2a22b22e28b9e49be3032f31.svg)
![$\sqrt{3} = [1;1,2,...];$](https://habrastorage.org/getpro/habr//formulas/890/732/38d/89073238d1833cecc83efd335d5033bd.svg)
![$ \sqrt{3}+1 = [2,1,...] $](https://habrastorage.org/getpro/habr//formulas/9bb/9bc/317/9bb9bc3176458cdbeea3eaa54a9397c3.svg)
![$\sqrt{5} = [2;4,4,4,...];$](https://habrastorage.org/getpro/habr//formulas/92f/dfa/d0b/92fdfad0bb0c8a39b1fd1a0302b49cce.svg)
![$ \sqrt{5}+2 = [4,4,4,...] $](https://habrastorage.org/getpro/habr//formulas/300/11b/542/30011b542099b3824078f63d9ebf6677.svg)
![$\sqrt{6} = [2;2,4,...]; $](https://habrastorage.org/getpro/habr//formulas/b8b/529/2f6/b8b5292f660b5720d727613ea0bd283d.svg)
![$ \sqrt{6}+2 = [4,2,...] $](https://habrastorage.org/getpro/habr//formulas/cad/f51/ad5/cadf51ad587ba3af73f5352333a8224e.svg)
![$\sqrt{13} = [3;1,1,1,1,6,...];$](https://habrastorage.org/getpro/habr//formulas/c7d/458/36d/c7d45836dee37fa1b7c705362296cb67.svg)
![$ \sqrt{13}+3 = [6,1,1,1,1,...] $](https://habrastorage.org/getpro/habr//formulas/01d/ec2/6ee/01dec26eeff6505fd49ca75ff18cf60a.svg)
Вычисление в облаке
WolframAlpfa производит вычисление цепных дробей с помощью операции continued fraction
Вычислим значение
ссылка
Вычислим значение
ссылка
Если в разложении корня по методу Бомбелли

к первому слагаемому прибавить , получим чисто периодическую дробь
, получим чисто периодическую дробь

Остаётся привести дробь к виду, в котором числителями дробей являются единицы
Разделив числитель и знаменатель дроби на , получим выражение
, получим выражение

![$ \sqrt{13}+3 = 6+ \frac{1}{\frac{6}{4} + \frac{1}{6 + \frac{1}{\frac{6}{4}+...} } } =[6,\frac{3}{2},...] $](https://habrastorage.org/getpro/habr//formulas/395/ebf/65f/395ebf65f62c4138f9d5ea1eb40fb7de.svg)
Алгоритм приближения цепной дроби![$ [6,\frac{3}{2},...] $](https://habrastorage.org/getpro/habr//formulas/867/cdc/276/867cdc276d9bfbb3006b5930a75fae35.svg)
На четвёртом шаге получаем , что равно
, что равно  в то время как
в то время как  .
.
Приближения к корню из натурального числа методом Ньютона
Итерационную формулу Герона можно получить методом Ньютона, проводя касательные к параболе
Подставим и
и  в уравнение
в уравнение 

Найдём точки пересечения параболы с осью
с осью 



Проведём через точку касательную к параболе
касательную к параболе
Производная функции равна
равна 
Значение функции в точке
Подставим эти значения в формулу
Получим прямую , которая является касательной к параболе
, которая является касательной к параболе  в точке
в точке 
Чтобы найти точку пересечения касательной с осью абсцисс приравняем к нулю левую часть уравнения
Отсюда
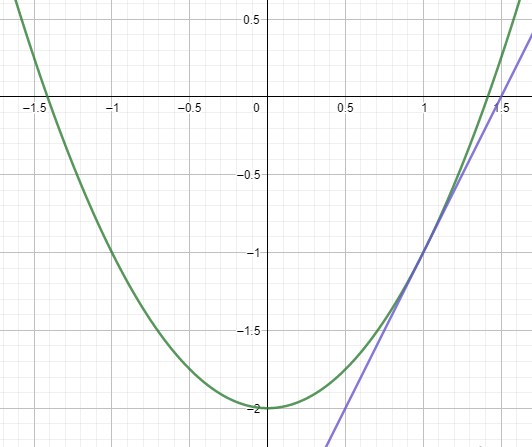
Проведем касательную в точке
Получим прямую
которая пересекает ось абсцисс в точке
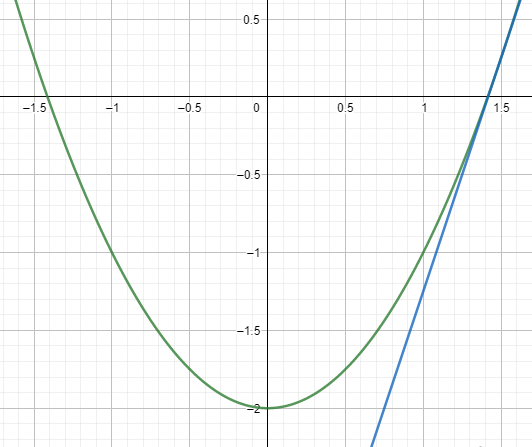
Следующая касательная пересечёт ось абсцисс в точке , и так далее…
, и так далее…
В статье «Геометрический смысл производной» представлен метод построения касательной, основанный на определении длины подкасательной
Цитата:
Обозначим через проекцию точки касания
проекцию точки касания  на ось
на ось  , а через
, а через  — точку, в которой касательная пересекает ось
— точку, в которой касательная пересекает ось  . Из прямоугольного треугольника
. Из прямоугольного треугольника  получаем:
получаем: 
или, поскольку


Используем данный метод для построения касательной к параболе в точке
в точке 
Длина отрезка , значит касательная пересекает ось абсцисс в точке
, значит касательная пересекает ось абсцисс в точке 
Построим прямую, проходящую через точки и
и 




Метод Диофанта или метод секущих
Пусть примыкающие друг к другу отрезки и
и  образуют диаметр полуокружности
образуют диаметр полуокружности
Пускай и
и  лежат в основании прямоугольных треугольников
лежат в основании прямоугольных треугольников
Направим из точки примыкания луч перпендикулярно диаметру
Пускай на луче лежит высота высекаемая полуокружностью
высекаемая полуокружностью
В силу подобия прямоугольных треугольников

Пускай отрезок и единичный отрезок
и единичный отрезок  лежат на оси
лежат на оси  , отрезок
, отрезок  лежит на оси
лежит на оси 
Тогда полуокружность обращается в ноль в точке
Пусть дана окружность , где
, где 
центр этой окружности лежит в точке
корни этой окружности лежат в точках

Проведём прямую
Эта прямая, помимо точки встретит окружность
встретит окружность  ещё в одной точке, координаты которой будут рациональными функциями от
ещё в одной точке, координаты которой будут рациональными функциями от 




Таким образом, каждому рациональному значению отвечает одна и только одна точка окружности
отвечает одна и только одна точка окружности 
Разделим на
на  :
:

Прямая пересечет ось абсцисс в точке
пересечет ось абсцисс в точке 
Подставляя угловые коэффициенты в уравнение прямой
в уравнение прямой  получим новые рациональные значения
получим новые рациональные значения  и новые точки окружности
и новые точки окружности  , отвечающие этим значениям
, отвечающие этим значениям
Направим из точки вертикальный луч
вертикальный луч
Пускай этот луч встречает окружность в точке
в точке 
Соединим начало координат с точками и
и  отрезками
отрезками  и
и 
Тогда угол


Косинус угла
Параметризация окружности
Проведём прямую под углом к оси абсцисс через точку
к оси абсцисс через точку 
Пускай прямая высекает на окружности точку
точку 

по теореме Фалеса об угле, опирающемся на диаметр окружности
Значит, угол наклона радиуса, проведённого к точке из центра окружности равен
из центра окружности равен 
Проведём прямую под тем же углом к оси абсцисс через начало координат
к оси абсцисс через начало координат
Пускай эта прямая высекает на прямой точку
точку 

Тогда


Отсюда выражаются координаты точки , заданные в параметрической форме
, заданные в параметрической форме

Пусть точка лежит на окружности радиуса
лежит на окружности радиуса 
выражение для ординаты точки заменится выражением
заменится выражением

Подставляя в эту формулу рациональные значения получим приближения к
получим приближения к 
Метод половинного деления или метод бисекции
Метод основан на теореме Больцано-Коши о нуле непрерывной функции

Пускай на выбранном отрезке функция возрастает и пускай точка
возрастает и пускай точка  делит отрезок пополам
делит отрезок пополам
Если функция в точке принимает положительное значение, значит она обращается в ноль слева от
принимает положительное значение, значит она обращается в ноль слева от  , если отрицательное — справа
, если отрицательное — справа
Повторяя деления многократно, получим последовательность вложенных промежутков, пределом которой будет корень , то есть число
, то есть число  , такое что
, такое что 
Определим функцию
функция бисекции принимает границы интервала![$ [a,b] $](https://habrastorage.org/getpro/habr//formulas/1a1/4ff/793/1a14ff79383191be0b3494b3911a7c03.svg) , а также количество итераций
, а также количество итераций  , вычисляет середину отрезка, определяет интервал, на котором функция
, вычисляет середину отрезка, определяет интервал, на котором функция  обращается в ноль, а затем рекурсивно вызывает саму себя с новыми параметрами
обращается в ноль, а затем рекурсивно вызывает саму себя с новыми параметрами
Метод хорд
Пускай на границах промежутка монотонная функция
монотонная функция  принимает значения разных знаков
принимает значения разных знаков
Пускай прямая соединяет точки
соединяет точки  и
и  и таким образом в точках
и таким образом в точках  и
и  прямая
прямая  принимает значения
принимает значения  и
и 
Коэффициент определяется соотношением
определяется соотношением

Тогда определяется соотношением
определяется соотношением

Добавлю, что значение неизвестных (переменных) величин и
и  определяется системой уравнений
определяется системой уравнений

Пускай прямая обращается в ноль в точке
обращается в ноль в точке  и пускай уже на границах промежутка
и пускай уже на границах промежутка  монотонная функция
монотонная функция  принимает значения разных знаков
принимает значения разных знаков
Соединим хордой точки и
и  , найдём точку
, найдём точку  пересечения хорды c осью
пересечения хорды c осью 
Повторяя приём многократно, найдём числа
Пределом данной последовательности будет корень
следующий алгоритм переопределяет переменную , вычисляя координаты точки пересечения прямой
, вычисляя координаты точки пересечения прямой  c отрезком
c отрезком 
Метод, представленный в журнале «Квант»⠀
Следующий метод основан на лемме об охотнике и зайцах, которая гласит, что если луч проходит через узел
проходит через узел  некоторой решётки, тогда найдётся такой узел, расстояние от которого до луча
некоторой решётки, тогда найдётся такой узел, расстояние от которого до луча  будет меньше любого наперёд заданного числа
будет меньше любого наперёд заданного числа 
Это означает, что для любого иррационального числа и любого положительного
и любого положительного  найдутся такие натуральные
найдутся такие натуральные  и
и  , что
, что 
Проведём прямую , где
, где 
Прямая пересекает каждую вертикальную прямую
пересекает каждую вертикальную прямую  в точке
в точке 
Найдём на прямой такую точку
такую точку  , что
, что  и
и 

Методы Васильева
к задаче из сборника «Прямые и кривые»
Пусть лестница, стоящая на гладком полу, соскальзывает вниз
Пускай буквами и
и  обозначаются точки соприкосновения лестницы со стеной и полом
обозначаются точки соприкосновения лестницы со стеной и полом
Пускай эти точки лежат на координатных осях, точка лежит в начале координат: таким образом вместе эти точки образуют прямоугольный треугольник
лежит в начале координат: таким образом вместе эти точки образуют прямоугольный треугольник 
По мере соскальзывания длины катетов приближаются некому общему значению (длина большего катета приближается по избытку, длина меньшего — по недостатку): когда угол наклона лестницы к стене и полу составит , треугольник
, треугольник  станет равнобедренным
станет равнобедренным

Обозначим сравнявшиеся по длине катеты буквой
Пусть
По теореме Пифагора
отсюда
пусть для ясности , а значит требуется найти приближения к корню из двух
, а значит требуется найти приближения к корню из двух
Пусть длина катета увеличивается дискретно на величину
увеличивается дискретно на величину  , иными словами
, иными словами 
пускай инкрементируется по достижении катетом
инкрементируется по достижении катетом  своего максимума, а приближение точки
своего максимума, а приближение точки  к отметке
к отметке  своего минимума
своего минимума
получим последовательность отрезков
0.1
0.2
0.3
0.4
…
По теореме Пифагора получим приближения к квадрату из тождества
из тождества 


значит
инкрементируем


значит
и так далее…
к задаче из журнала «Квант»

Метод прямого счёта позволяет определить, что за первые оборотов
оборотов ![$[n \cdot \sqrt{2}] $](https://habrastorage.org/getpro/habr//formulas/447/c88/1cc/447c881cc4dcddf6f52a705c21e29d3d.svg) красных точек «перейдут в различные точки окружности»
красных точек «перейдут в различные точки окружности»
Пускай равно количеству красных точек, оставляемых на
равно количеству красных точек, оставляемых на  отрезках длины
отрезках длины
Подставляя эти числа в уравнение найдём последовательность наилучших приближений
найдём последовательность наилучших приближений  к корню из двух
к корню из двух
Уточню, что является иррациональным, если
является иррациональным, если  не является точным квадратом
не является точным квадратом
Доказательство иррациональности («Квант» 1974)
(«Квант» 1974)
Пусть дано уравнение
Здесь каждая новая пара выражается через предыдущую подстановкой в рекуррентную формулу


Получившиеся приближение было известно ещё математикам древней Индии
было известно ещё математикам древней Индии
Пусть функция определена полиноминальным уравнением степени
определена полиноминальным уравнением степени 
Полином ой степени от переменной
ой степени от переменной  есть сумма вида
есть сумма вида 
Точки пересечения квадратичной функции с осью абсцисс определяются выражением
Пускай число является корнем
является корнем 
Говорят, что делится на
делится на  , если справедливо тождество
, если справедливо тождество 
Теорема Безу гласит, что
Пусть
Тогда
Из этого равенства мы видим, что равно нулю, если
равно нулю, если  равно нулю, то есть если число
равно нулю, то есть если число  — корень
— корень 
Определим экстремум функции согласно лемме Ферма
согласно лемме Ферма


Дискриминант определяется подстановкой в функцию
в функцию 

Поскольку где остаток
где остаток 
Отсюда
Путём понижения степени придём к выражению
 отсюда
отсюда 

Подставим в функцию
в функцию 
Тогда




Теорема Виета гласит, что


Метод резольвент
Сумма и произведение корней уравнения равны
равны


коэффициенты и
и  связаны соотношением
связаны соотношением


Подставив числовые значения в уравнение, получим

Значит


Тогда


а значит число равно
равно

Подробнее об этом методе решения здесь
Метод Лобачевского позволяет найти приближённое значение одного из корней
Пусть


Произведём замену


Таким образом корни исходного уравнения «возводятся в квадрат»
По теореме Виета сумма «возведённых» корней будет равна
Если повторить этот приём многократно, корни «возведутся» в четвёртую, восьмую, шестнадцатую и т.д. степень
Один из корней станет пренебрежимо мал по сравнению с другим, тогда оставшийся корень станет приближённо равен абсолютному значению второго коэффициента квадратного уравнения , возведённого в некую высшую степень
, возведённого в некую высшую степень
Коэффициенты этого уравнения связаны с коэффициентами уравнений низших степеней величинами и
и 


Пусть и
и 
Тогда
По теореме Виета
а значит




найдём значение по формуле
по формуле

Лемма Ферма утверждает, что производная дифференцируемой функции в точке экстремума равна нулю
Её касательная в данной точке параллельна оси абсцисс
Следуя данному правилу, найдём экстремум функции





Согласно теореме Ролля экстремум функции лежит между точками
лежит между точками  и
и  , такими что
, такими что 
Пусть точка лежит на оси ординат, то есть
лежит на оси ординат, то есть 
Проведём через точку горизонтальную прямую
горизонтальную прямую
Пускай эта прямая встречает параболу в точке
Точки и
и  высекут на этой прямой отрезок
высекут на этой прямой отрезок
Ось параболы разделит отрезок пополам
пополам
Пусть дана парабола
Будем сдвигать параболу вертикально вниз до тех пор, пока произведение корней не превысит некий порог, который по теореме Виета равен

Пускай расстояние между корнями изменяется дискретно
определим переменную step, равную данной дискретной величине
Пускай «длина шага» уменьшается на порядок перед тем, как произведение корней покинет интервал
При длине шага число
число 
уменьшаем размер шага на порядок

ещё на порядок

и так далее…
Согласно Лагранжу, первые основы динамики были заложены Галилеем
Полученная Галилео Галилеем формула определяет квадратичную зависимость расстояния от времени при равноускоренном/равнозамедленном движении материальной точки вдоль координатной оси
определяет квадратичную зависимость расстояния от времени при равноускоренном/равнозамедленном движении материальной точки вдоль координатной оси
Пускай начальная координата материальной точки начальная скорость
начальная скорость  ускорение
ускорение 
Отрицательная величина скорости означает, что в начальный момент времени материальная точка движется противоположно направлению координатной оси
Такое движение определяется уравнением
за время материальная точка замедляется до полной остановки, затем ускоряется и проходит путь
материальная точка замедляется до полной остановки, затем ускоряется и проходит путь  за время
за время 
Тогда общее время в пути до момента встречи с осью абсцисс составляет
P.S.
Следующая задача из сборника Арнольда рассматривается в статье журнала «Квант» Удивительные приключения периодических дробей
27. Доказать, что остаток от деления числа на простое нечетное число
на простое нечетное число
 равен
равен 
(примеры: .
.
P.P.S. Статья о цепных дробях «Об одной задаче, которую больше не предлагают на собеседовании» ссылка
Задачи для детей от 5 до 15 лет В. И. Арнольд
Курс дифференциального и интегрального исчисления Г. М. Фихтенгольц
Теория чисел А. А. Бухштаб
За страницами учебника математики Н. Я. Виленкин, Л. П. Шибасов, З. Ф. Шибасова
Алгебра Н. Я. Виленкин, Р. С. Гутер, С. И. Шварцбурд
Что такое производная Н. Я. Виленкин, А. Г. Мордкович, журнал «Квант»
Диофант и диофантовы уравнения И.Г. Башмакова
Пьер Ферма И.Г. Башмакова, журнал «Квант»
Диофантовы уравнения и рациональные точки М.И. Башмаков, журнал «Квант»
Геометрический смысл производной А.Я. Хинчин, журнал «Квант»
Занимательная геометрия Я.И. Перельман
Метод математической индукции И.С. Соминский
Число Фидия — золотое сечение А.П. Савин, журнал «Квант»
Числа Фибоначчи Н. Н. Воробьёв
Числа Фибоначчи А. Спивак, журнал «Квант»
Уравнения Пелля В. Сендеров, А. Спивак, журнал «Квант»
Золотое сечение А. Д. Бендукидзе, журнал «Квант»
Решётки и правильные многоугольники А. Егоров, журнал «Квант»
Числа и многочлены С. Ашманов, журнал «Квант»
Сколько корней у многочлена? С. Табачников, журнал «Квант»
Уравнения, которые удается решить А. Тоом, журнал «Квант»
Формулы Виета Ц.С. Копрински, журнал «Квант»
История о том, как Галилей открыл законы движения С. Гиндикин, журнал «Квант»
Метод Лобачевского А.Л. Брудно, журнал «Квант»
Прямые и кривые Н.Б. Васильев, В.Л. Гутенмахер
Пределы, непрерывность Н.Я. Виленкин, А.Г. Мордкович
Пределы А.А. Кириллов
Что такое математика? В.И. Арнольд
Что такое математика? Курант Р., Роббинс Г.
Digital Arithmetic Ercegovac Milos D., Lang Tomas
О книге с большой буквы А. Щетников, журнал «Квантик»
В сборнике Арнольда есть следующая задача
38. Вычислить сумму:
(с ошибкой не более 1% от ответа)
Ниже представлен алгоритм для вычисления частичных сумм этого ряда на языке Scheme (Lisp) в обыкновенных дробях
#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000)
Два последних примера drRacket вычислил с ошибкой

#python def series_sum(n): if n==0: return 0 else: return 1.0/(n*(n+1.0))+series_sum(n-1.0) print(series_sum(10)) print(series_sum(100))
Можно заметить, что частичная сумма первых
Доказательство по индукции
1. При
2. Предположим, что гипотеза верна и для
где
Установим справедливость и при
Доказательство методом перебора
Пусть дана последовательность
Предположим, что частичная сумма первых
Тогда
Отсюда
Пятясь назад, придём к
Теорема Вейерштрасса гласит
Если последовательность монотонна и ограничена, то она сходитсяданная последовательность возрастает, поскольку
данная последовательность ограничена сверху, поскольку
отобразим целочисленные координаты оси
отобразим полученные точки на график функции
получим систему вложенных отрезков с неподвижной точкой

Кстати, данные частичные суммы
Другим представлением египетской дроби является сумма
где
А также сумма
где
(«Квант» 1970)
| |
|||
|---|---|---|---|
Числа Фибоначчи
В следующей задаче требуется найти НОД двух соседних чисел Фибоначчи
43.Числа кроликов («Фибоначчи»), образуют последовательность
Для решения данной задачи достаточно доказать, что два соседних числа Фибоначчи взаимно просты, то есть доказать справедливость тождества
Доказательство из книги «За страницами учебника математики» [10-11]
Из равенстваследует, что
. Пятясь таким образом назад, придём к
, а потому два соседних числа Фибоначчи взаимно просты.
Добавлю, что
где
и в данном конкретном случае
Доказательство из книги «Числа Фибоначчи» Н. Н. Воробьёва
Пусть некоторое числоявляется делителем чисел
и
. Тогда и их разность
будет делиться на
.
Пятясь таким образом назад, придём к тому, что набудут делиться и
и
и так далее, а значит и
должно делиться на
, а значит два соседних числа Фибоначчи взаимно просты
Тожество Кассини
Похожий метод, метод перебора последовательности
Предположим, что
Перебрав последовательность в обратном направлении, придём к тому, что левая и правая части данного равенства обе тождественны единице
Доказательство
Домножим тождество
Вычтем
Данное выражение показывает, что некая величина, которой тождественны левая и правая части равенства, меняет свой знак на противоположный при переходе
и т.д.
Приближения к золотому сечению
В следующей задаче необходимо вычислить золотое сечение,
53. Для последовательности чисел Фибоначчи
Отметим на числовой оси отрезки

Числа
Числа
По лемме о вложенных промежутках (Курс дифференциального и интегрального исчисления, 38)
А значит
Разделив
После замены
получится квадратное уравнение
Различные методы решения этого уравнения приводятся ниже, в отдельном разделе, посвящённом решению квадратных уравнений
Если в программе geogebra соединить дугами о��ружности точки 2 и

Для сравнения

Кстати, в правильной пятиконечной звезде (звёздчатом пятиугольнике) каждый отрезок делится другим отрезком, пересекающим его, в золотом сечении

В самом деле, так как треугольники ACD и ABE подобны, то AC:AB=AD:AE. Но AD=BC, а AE=AC, и поэтому AC:AB=BC:AC — уже известная нам пропорция золотого сечения.
В правильном пятиугольнике отношение диагонали к стороне также равно
Вообще, существует стандартный алгоритм вычисления чисел Фибоначчи на Python
(алгоритм представлен на сайте Python.org)
def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100)
Приближения к
def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(12)
На двенадцатом шаге получим приближение 1.61805
Формула Бине использует
Можно заметить, что второе слагаемое всегда меньше единицы при любом целом неотрицательном
Поэтому, зная, что формула Бине даёт целые числа, можно утверждать справедливость тождества, в котором данная дробь округляется до ближайшего целого

Пусть
Тогда выражения вида
то есть
Приняв
получим приближение
Алгоритм вычисления
#python a=b=1 t=2 for i in range(n): A=a+5*b B=a+b t=t*2 a=A b=B print ((a+b*5**0.5)/(t*5**0.5))
n=10 Fn=88.99775275224582
Цепные дроби
Если в уравнении
Продолжая производить замены, придём к представлению золотого сечения в виде цепной дроби
Задача из учебника SICP
Упражнение 1.35.
Покажите, что золотое сечение
пример вычисления факториала
(define ! (lambda (n) (if (= n 0) 1 (* n (! (- n 1)))))) (display (! 5))
Алгоритм решения задачи 1.35
(define fixed-point (lambda (n) (if (> n 10) 1 (+ 1 (/ 1.0 (fixed-point (+ n 1))))))) (display (fixed-point 1) )
Сперва опишем счётчик, инкрементирующий переменную
(do ((i 1 (+ 1 i))) ((> i 10)) (display i)(newline))
Оператор set! позволяет переопределить значение глобальной переменной
Определим глобальную переменную fixed-point и будем переопределять значение данной переменной в цикле do c помощью оператора set!
(define fixed-point 1) (do ((i 1 (+ 1 i))) ((> i 10)) (set! fixed-point (+ 1 (/ 1.0 fixed-point))) (display fixed-point) (newline))
#python arr=[1.0] def foo(a): b=1.0+1.0/(1.0+1.0/a[len(a)-1]) return b arr.append(foo(arr)) #первый шаг arr.append(foo(arr)) #второй шаг arr.append(foo(arr)) #третий шаг print (arr)
Задачник Арнольда
54. Вычислить бесконечную цепную дробь
Решение
Рассмотрим уравнение
Согласно теоремам 236 и 235 из книги «Теория чисел»:
Составляем таблицу значений
| 1 | 2 | |
|---|---|---|
| P | 1 | 3 |
| Q | 1 | 2 |
так что
и поскольку
Пусть дана последовательность
Для этой последовательности справедливо равенство
Далее надо доказать само существование предела
поскольку, если этот предел существует, то он должен равняться числу
Для доказательства существования применим аксиому Больцано-Вейерштрасса. В самом деле, можно доказать по индукции, что при любом
Поэтому последовательностьмонотонна и ограничена
Здесь показатели степеней представляют геометрическую прогрессию, то есть
При перемножении степеней с одинаковыми основаниями показатели степеней складываются
Сумма геометрической прогрессии
Легко понять, чтоотличается от
на
и что эта разность становится сколь угодно малой или «стремится к нулю» при неограниченном возрастании
На рисунке ниже

#python def foo(n,a): temp=a while(n>0): a=temp*(a**0.5) #a=temp+(a**0.5) n=n-1 return a**0.5 print(foo(50,2)) #1.9999999999999993
Если уравнение
Тогда
Данное выражение является частным случаем варианты
Курс дифференциального и интегрального исчисления, 35 (2)
Таким образомполучается из
по формуле
… По основной теореме, вариантаимеет некий конечный предел
. Для определения его перейдём к пределу в равенстве
Мы получим, таким образом, чтоудовлетворяет квадратному уравнению
Уравнение это имеет корни разных знаков; но интересующий нас пределне может быть отрицательным, следовательно, равен именно положительному корню:
То есть
Далее в «Курсе дифференциального и интегрального исчисления», 35(3) рассматривается алгоритм вычисления обратного числа (такого числа 1/с, произведение которого на данное число с равно единице)
Пусть— любое положительное число, и положим
Написанное выше рекуррентное соотношение заменится таким:
Взяв начальное значениепод условием:
, получим, что
, монотонно возрастая, будет стремиться к
. По этой схеме на счётных машинах и вычисляется число, обратное
.
#python def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr
Функция reciprocal принимает на вход число
и т.д.
Примеры работы функции reciprocal при подстановке в переменную
>>> reciprocal(3,0.1,5) [0.1, 0.17, 0.2533, 0.31411733000000003, 0.3322255689810133] >>> reciprocal(5,0.1,5) [0.1,0.15000000000000002,0.18750000000000003,0.19921875000000003,0.19999694824218753] >>> reciprocal(8,0.1,5) [0.1,0.12,0.1248,0.12499968,0.1249999999991808]
Геометрическое представление о данном алгоритме даёт метод Ньютона или метод касательных
Пусть дано уравнение прямой
Уравнение прямой, проходящей через точку
Тогда
Так как угловой коэффициент касательной к графику дифференцируемой функции в точке с абсциссой
Производной функции
Для гиперболы
Знаменатель состоит из двух слагаемых, второе при малых значениях
Касательными
Подставляя числа

Если сдвинуть гиперболу вниз на
Уравнение касательных преобразуется в
Далее, приравняв уравнение касательной к нулю и выразив
Вместо
Вместо
Получим выражение
Раскрыв скобки, получим
Подставим
Пусть
Тогда округлённая обратная величина будет равна
Подставим эти значения в уравнение
Касательные
с каждой новой итерацией будут всё ближе к искомой величине

Заголовок спойлера
Преобразуем

и возведём это уравнение в квадрат, чтобы получить квадратную параболу

Все параболы данного вида будут иметь с осью абсцисс одну общую точку (точку касания), равную
Для того, чтобы найти приближения к точке касания, надо взять производную этой функции
Производная будет равна
Тогда касательными к параболе будут функции вида
Пусть требуется найти приближения к
Тогда параболой будет функция
Касательными будут функции

В точке касательной будет
касательной будет 
Первым приближением будет
Подставив это значение в уравнение касательной, получим

Касательная пересечёт ось абсцисс в точке
Приравняв к нулю и выразив
к нулю и выразив  в уравнении касательной, получим уравнение, позволяющее получать новые приближения
в уравнении касательной, получим уравнение, позволяющее получать новые приближения
Напишем функцию, которая вычисляет данное значение при различных
Добавим в функцию переменную, равную количеству рекурсивных вызовов функции
получим приближение, равное
Далее этот алгоритм используется для подсчёта приближений в обыкновенных дробях на Scheme
Обработка переменных в цикле производится следующим образом
Далее do_cycle используется для вычисления приближений в цикле
Если ограничиться однократным вычислением производной в точке начального приближения, то пересечения прямых, параллельных касательной с осью абсцисс дадут новые приближения
с осью абсцисс дадут новые приближения
Подставив значение в уравнение параболы
в уравнение параболы  получим значение, на которое требуется сдвинуть касательную
получим значение, на которое требуется сдвинуть касательную
Новой касательной будет

а следующим приближением будет точка пересечения этой касательной с осью абсцисс

Подставив это значение в уравнение параболы получим значение, на которое необходимо сдвинуть касательную по оси ординат
получим значение, на которое необходимо сдвинуть касательную по оси ординат
Алгоритм
Пусть proxima — это последовательные приближения
b_coef — это коэффициент, на который сдвигается касательная по оси абсцисс
parabola() — это параболическая функция
Результат
Предположим, что свободные коэффициенты касательных являются рациональными числами, то есть . Тогда
. Тогда  , поскольку является результатом деления коэффициента
, поскольку является результатом деления коэффициента  на натуральное число
на натуральное число
При подстановке proxima в получим число рациональное. Тогда
получим число рациональное. Тогда  по предположению
по предположению
В обыкновенных дробях
Модифицированный метод касательных
Преобразуем
и возведём это уравнение в квадрат, чтобы получить квадратную параболу
Все параболы данного вида будут иметь с осью абсцисс одну общую точку (точку касания), равную
Для того, чтобы найти приближения к точке касания, надо взять производную этой функции
Производная будет равна
Тогда касательными к параболе будут функции вида
Пусть требуется найти приближения к
Тогда параболой будет функция
Касательными будут функции
В точке
Первым приближением будет
Подставив это значение в уравнение касательной, получим
Касательная пересечёт ось абсцисс в точке
Приравняв
Напишем функцию, которая вычисляет данное значение при различных
#python def foo(x_null): x=(9.0*x_null**2.0-1.0)/(18.0*x_null-6.0) return x print (foo(foo(foo(foo(foo(foo(foo(0))))))))
(define (foo x)( /(-(* 9 (* x x))1)(- (* 18 x) 6) )) (display (foo(foo(foo(foo(foo(foo(foo 0))))))))
Добавим в функцию переменную, равную количеству рекурсивных вызовов функции
def foo(x_null,i): i=i-1 x=(9.0*x_null**2.0-1.0)/(18.0*x_null-6.0) print(x) if i>=0: foo(x,i) foo(0,7)
получим приближение, равное
Далее этот алгоритм используется для подсчёта приближений в обыкновенных дробях на Scheme
Обработка переменных в цикле производится следующим образом
(define (do_cycle n) (do ((i 1 (+ i 1))) ((> i n) ) (display i)(display " ") )) (do_cycle 10)
Далее do_cycle используется для вычисления приближений в цикле
(define (foo x)( /(-(* 9 (* x x))1)(- (* 18 x) 6) )) (define x0 0) (define (do_cycle n) (do ((i 1 (+ i 1))) ((> i n) ) (foo x0)(set! x0 (foo x0)) )) (do_cycle 7) (display x0)
Если ограничиться однократным вычислением производной в точке начального приближения, то пересечения прямых, параллельных касательной
Подставив значение
Новой касательной будет

а следующим приближением будет точка пересечения этой касательной с осью абсцисс
Подставив это значение в уравнение параболы
Алгоритм
Пусть proxima — это последовательные приближения
b_coef — это коэффициент, на который сдвигается касательная по оси абсцисс
parabola() — это параболическая функция
proxima=0.17 b_coef=1.0 def parabola(x): return 9.0*x*x-6.0*x+1.0 i=0 while i<=100000: b_coef = b_coef+parabola(proxima) proxima = b_coef/6.0 i=i+1 print(proxima)
Результат
Предположим, что свободные коэффициенты касательных являются рациональными числами, то есть
При подстановке proxima в
В обыкновенных дробях
(define proxima 1/6) (define b_coef 1) (define (parabola x)( +( -(* 9 (* x x))(* 6 x))1 ) ) (define (do_cycle n) (do ((i 1 (+ i 1))) ((> i n) ) (set! b_coef (+ b_coef (parabola x0))) (set! proxima (/ b_coef 6)) )) (do_cycle 5) (display proxima)
Итерационный метод Герона для извлечения квадратного корня из числа
Пусть
Пусть
Проведём горизонтальную прямую через точку
Прямая
Пусть точка
… точка
… точка
Последовательность

Проецируя эти приближения на ось
Слева от
Формулу Герона можно получить из формулы общего вида
подставив в эту формулу числовое значение (натуральное число). В данном конкретном случае, поскольку необходимо вычислить корень квадратный, надо подставить число два.
В книге «Занимательная геометрия» сообщается другой старинный способ извлечения квадратного корня
Цитата:
Пусть надо вычислить
Итак,
Квадрат дроби
Значит, приближенно
Если мы хотим определить значение корня ещё точнее, напишем уравнение
Отсюда
Отбросив
Следовательно, во втором приближении
Третье приближение находим тем же приемом и т.д.
Вычисление квадратного корня с помощью цепных дробей использовал Рафаэль Бомбелли
Цитата:
Чтобы найти значение
Тогда
следующий алгоритм использует разложение в цепную дробь
#python arr=[] def square_root(n,a,n_count): # n-подкоренное значение, a - целая часть корня x0=a # первое приближение равно a global arr for i in range(n_count): # результат будет больше искомой величины на a arr.append(x0-a) # вычитаем a x0=2*a+(n-a*a)/x0
Способ выделения целой части позволяет представить иррациональное число в виде бесконечной цепной дроби с частыми числителями, равными единице
Вот пример разложения в цепную дробь числа
Цитата:
Таким образом
Выделим целую часть числа
В итоге получилось:
Проделаем еще один аналогичный шаг:
Нетрудно заметить, что процесс выделения целой части и образования цепной дроби в данном примере не имеет конца. В каждом новом знаменателе будет появляться
Гипотеза
Если
Эта гипотеза представлена в трудах Эвариста Галуа
Так чисто периодическая дробь
Вычисление в облаке
WolframAlpfa производит вычисление цепных дробей с помощью операции continued fraction
Вычислим значение
ссылка
Вычислим значение
ссылка
Если в разложении корня по методу Бомбелли
к первому слагаемому прибавить
Остаётся привести дробь к виду, в котором числителями дробей являются единицы
Разделив числитель и знаменатель дроби на
Алгоритм приближения цепной дроби
#lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4)
На четвёртом шаге получаем
Приближения к корню из натурального числа методом Ньютона
Итерационную формулу Герона можно получить методом Ньютона, проводя касательные к параболе
Подставим
Найдём точки пересечения параболы
Проведём через точку
Производная функции
Значение функции в точке
Подставим эти значения в формулу
Получим прямую
Чтобы найти точку пересечения касательной с осью абсцисс приравняем к нулю левую часть уравнения
Отсюда

Проведем касательную в точке
Получим прямую
которая пересекает ось абсцисс в точке

Следующая касательная пересечёт ось абсцисс в точке
В статье «Геометрический смысл производной» представлен метод построения касательной, основанный на определении длины подкасательной
Цитата:
Обозначим через
или, поскольку

Используем данный метод для построения касательной к параболе
Длина отрезка
Построим прямую, проходящую через точки
#python def f(x): f=x**2-2 return f def Df(x): Df=2*x return Df x=1 for i in range(10): x=x-f(x)/Df(x) print(x)
Метод Диофанта или метод секущих
Пусть примыкающие друг к другу отрезки
Пускай
Направим из точки примыкания луч перпендикулярно диаметру
Пускай на луче лежит высота
В силу подобия прямоугольных треугольников

Пускай отрезок
Тогда полуокружность обращается в ноль в точке
Пусть дана окружность
центр этой окружности лежит в точке
корни этой окружности лежат в точках

Проведём прямую
Эта прямая, помимо точки
Таким образом, каждому рациональному значению
Разделим
Прямая
Подставляя угловые коэффициенты
#python def approx(n): k=1 for i in range(10): approx=(k*(n+1))/(k**2+1) print(approx) k=(k**2+1)/(k*(n+1))
Направим из точки
Пускай этот луч встречает окружность
Соединим начало координат с точками
Тогда угол

Косинус угла
Параметризация окружности
Проведём прямую под углом
Пускай прямая высекает на окружности

по теореме Фалеса об угле, опирающемся на диаметр окружности
Значит, угол наклона радиуса, проведённого к точке
Проведём прямую под тем же углом
Пускай эта прямая высекает на прямой

Тогда
Отсюда выражаются координаты точки
Пусть точка
выражение для ординаты точки
Подставляя в эту формулу рациональные значения
Метод половинного деления или метод бисекции
Метод основан на теореме Больцано-Коши о нуле непрерывной функции
Если функция непрерывна на некотором отрезке и на границах этого отрезка принимает значения противоположных знаков, то существует точка, в которой функция обращается в ноль
Пускай на выбранном отрезке функция
Если функция в точке
Повторяя деления многократно, получим последовательность вложенных промежутков, пределом которой будет корень
Определим функцию
def y(x): return x*x-2
функция бисекции принимает границы интервала
def bisection(a, b, i): i=i-1 # уменьшаем количество итераций middle=(a+b)/2.0 # делим отрезок пополам print(middle) if i>0: if(y(a)*y(middle)<0): # определяем нужный отрезок bisection(a,middle,i) if(y(middle)*y(b)<0): bisection(middle,b,i) #загружаем в функцию новые значения
Метод хорд
Пускай на границах промежутка
Пускай прямая
Коэффициент
Тогда
Добавлю, что значение неизвестных (переменных) величин

Пускай прямая
Соединим хордой точки
Повторяя приём многократно, найдём числа
Пределом данной последовательности будет корень
следующий алгоритм переопределяет переменную
#python def f(x): f=x**2-2 return f def k(A,B): k=(f(B)-f(A))/(B-A) return k def b(B,A): b=f(B)-k(A,B)*B return b def a(A,B): a=-b(A,B)/k(A,B) return a approx=a(1,2) print(approx) for i in range(10): approx=a(approx,2) print(approx)
Метод, представленный в журнале «Квант»⠀
Следующий метод основан на лемме об охотнике и зайцах, которая гласит, что если луч
Это означает, что для любого иррационального числа
Проведём прямую
Прямая
Найдём на прямой
# python for m in range(1,20): for n in range(m,20): if n**2/m**2>2: print('n / m=',n,'/',m) break

Методы Васильева
к задаче из сборника «Прямые и кривые»
Пусть лестница, стоящая на гладком полу, соскальзывает вниз
Пускай буквами
Пускай эти точки лежат на координатных осях, точка
По мере соскальзывания длины катетов приближаются некому общему значению (длина большего катета приближается по избытку, длина меньшего — по недостатку): когда угол наклона лестницы к стене и полу составит

Обозначим сравнявшиеся по длине катеты буквой
Пусть
По теореме Пифагора
отсюда
пусть для ясности
Пусть длина катета
пускай
получим последовательность отрезков
0.1
0.2
0.3
0.4
…
По теореме Пифагора получим приближения к квадрату
значит
инкрементируем
значит
и так далее…
к задаче из журнала «Квант»
Пусть красными точками на прямой отмечены натуральные числа
Намотаем прямую на окружность длины, начав с точки
Ясно, что различные красные точки прямой перейдут при этом в различные точки окружности, поскольку равенствопри целых
невозможно (ведь число
иррационально)

Метод прямого счёта позволяет определить, что за первые
Пускай
#python m=0 # количество красных точек n=0 # количество оборотов while n<10: n=n+1 m=m+1 if (m+1)<n*2**0.5: m=m+1 print(m,"/",n)
Подставляя эти числа в уравнение
Уравнения Пелля
Пусть натуральное числоне является квадратом. Легко видеть, что
не выражается отношением натуральных чисел, т.е. не существует такой обыкновенной дроби
, что
. Другими словами, если натуральное число
не является точным квадратом, то уравнение
не имеет решения в натуральных числах.
Попытаемся в этом случае выразитьотношением натуральных чисел приближённо. Если
, то
. Самое близкое к нулю натуральное число — это единица. Поэтому дело сводится к решению в натуральных числах диофантова уравнения
которое носит название… уравнения Пелля
Уточню, что
Доказательство иррациональности
Пусть дано число, и
, где
и
— натуральные числа.
Пусть дробь— несократимая (ведь любую дробь можно сокращать, пока у числителя и знаменателя не сократятся все общие делители).
Тогда
В левой части стоит несократимая дробь (ведьи
не имеют общих делителей), а в правой части уравнения — заведомо целое число. Но дробное число не может быть равно целому.
Значит,… числоне является рациональным, откуда следует, что оно иррациональное, что и требовалось доказать.
Пусть дано уравнение
Подбором найдём несколько решенийили

Здесь каждая новая пара выражается через предыдущую подстановкой в рекуррентную формулу
x0=1 y0=1 x=0 y=0 i=0 while i<=6: y=x0+y0 x=2*y0+x0 x0=x y0=y i=i+1 print(x) print(y)
Получившиеся приближение
Корни квадратичной функции
Пусть функция
Полином
Точки пересечения квадратичной функции с осью абсцисс определяются выражением
Пускай число
Говорят, что
Теорема Безу гласит, что
остатокот деления
на
равен

Пусть
Тогда
Из этого равенства мы видим, что
Определим экстремум функции
Дискриминант определяется подстановкой
Поскольку
Отсюда
Путём понижения степени придём к выражению

Подставим
Тогда
Теорема Виета гласит, что
сумма корней приведённого квадратного уравнения равна второму коэффициенту с противоположным знаком, а их произведение равно свободному коэффициенту
Метод резольвент
Сумма и произведение корней уравнения
коэффициенты
Подставив числовые значения в уравнение, получим
Значит
Тогда
а значит число
Подробнее об этом методе решения здесь
Метод Лобачевского позволяет найти приближённое значение одного из корней
Пусть
Произведём замену
Таким образом корни исходного уравнения «возводятся в квадрат»
По теореме Виета сумма «возведённых» корней будет равна
Если повторить этот приём многократно, корни «возведутся» в четвёртую, восьмую, шестнадцатую и т.д. степень
Один из корней станет пренебрежимо мал по сравнению с другим, тогда оставшийся корень станет приближённо равен абсолютному значению второго коэффициента квадратного уравнения
Коэффициенты этого уравнения связаны с коэффициентами уравнений низших степеней величинами
Пусть
Тогда
По теореме Виета
а значит
найдём значение
#python a=4870847 x=2 for i in range(10): x=(a+31*x**32)/(32*x**31) print(x)
Лемма Ферма утверждает, что производная дифференцируемой функции в точке экстремума равна нулю
Её касательная в данной точке параллельна оси абсцисс
Для нахождения экстремумов многочленаФерма предлагает следующее правило:
1) подставляем ввместо
выражение
;
2) приравниваеми
;
3) после приведения подобных членов сокращаем на;
4) полагаем.
В результате получаем равенство. Ферма утверждает, что все значения
, при которых многочлен
имеет экстремум, необходимо являются корнями уравнения
Сама функция
, которая по правилу Ферма получается чисто алгебраически (т.е. без предельного перехода), теперь называется производной от
.
Следуя данному правилу, найдём экстремум функции
Согласно теореме Ролля экстремум функции
Пусть точка
Проведём через точку
Пускай эта прямая встречает параболу в точке
Точки
Ось параболы разделит отрезок
Пусть дана парабола
Будем сдвигать параболу вертикально вниз до тех пор, пока произведение корней не превысит некий порог, который по теореме Виета равен

Пускай расстояние между корнями изменяется дискретно
определим переменную step, равную данной дискретной величине
def foo(x1,x2,step): x1=x1+step // прибавляем шаг x2=x2+step if x1*x2<1: foo(x1,x2,step) else: print(x2-step) #декремент шага foo(0,1,0.1)
Пускай «длина шага» уменьшается на порядок перед тем, как произведение корней покинет интервал
else: print(x2-step) #декремент шага x1=x1-step x2=x2-step step=step/10 #уменьшаем размер шага на порядок foo(x1,x2,step)
При длине шага
уменьшаем размер шага на порядок
ещё на порядок
и так далее…
Согласно Лагранжу, первые основы динамики были заложены Галилеем
Полученная Галилео Галилеем формула
Пускай начальная координата материальной точки
Отрицательная величина скорости означает, что в начальный момент времени материальная точка движется противоположно направлению координатной оси
Такое движение определяется уравнением
за время
Тогда общее время в пути до момента встречи с осью абсцисс составляет
P.S.
Следующая задача из сборника Арнольда рассматривается в статье журнала «Квант» Удивительные приключения периодических дробей
27. Доказать, что остаток от деления числа
(примеры:
P.P.S. Статья о цепных дробях «Об одной задаче, которую больше не предлагают на собеседовании» ссылка
Книги
Задачи для детей от 5 до 15 лет В. И. Арнольд
Курс дифференциального и интегрального исчисления Г. М. Фихтенгольц
Теория чисел А. А. Бухштаб
За страницами учебника математики Н. Я. Виленкин, Л. П. Шибасов, З. Ф. Шибасова
Алгебра Н. Я. Виленкин, Р. С. Гутер, С. И. Шварцбурд
Что такое производная Н. Я. Виленкин, А. Г. Мордкович, журнал «Квант»
Диофант и диофантовы уравнения И.Г. Башмакова
Пьер Ферма И.Г. Башмакова, журнал «Квант»
Диофантовы уравнения и рациональные точки М.И. Башмаков, журнал «Квант»
Геометрический смысл производной А.Я. Хинчин, журнал «Квант»
Занимательная геометрия Я.И. Перельман
Метод математической индукции И.С. Соминский
Число Фидия — золотое сечение А.П. Савин, журнал «Квант»
Числа Фибоначчи Н. Н. Воробьёв
Числа Фибоначчи А. Спивак, журнал «Квант»
Уравнения Пелля В. Сендеров, А. Спивак, журнал «Квант»
Золотое сечение А. Д. Бендукидзе, журнал «Квант»
Решётки и правильные многоугольники А. Егоров, журнал «Квант»
Числа и многочлены С. Ашманов, журнал «Квант»
Сколько корней у многочлена? С. Табачников, журнал «Квант»
Уравнения, которые удается решить А. Тоом, журнал «Квант»
Формулы Виета Ц.С. Копрински, журнал «Квант»
История о том, как Галилей открыл законы движения С. Гиндикин, журнал «Квант»
Метод Лобачевского А.Л. Брудно, журнал «Квант»
Прямые и кривые Н.Б. Васильев, В.Л. Гутенмахер
Пределы, непрерывность Н.Я. Виленкин, А.Г. Мордкович
Пределы А.А. Кириллов
Что такое математика? В.И. Арнольд
Что такое математика? Курант Р., Роббинс Г.
Digital Arithmetic Ercegovac Milos D., Lang Tomas
О книге с большой буквы А. Щетников, журнал «Квантик»