
Введение
Когда происходит рисование точки, линии или сложного полигона в трехмерном мире, финальный результат, в конечном итоге, будет изображен на плоском, двухмерном экране. Соответственно, трехмерные объекты проходят некий путь преобразования, превращаясь в набор пикселей, выводимых в двумерное окно.
Развитие программных инструментов, реализующих трехмерную графику пришло, вне зависимости от того, какой из них вы выбираете, примерно к одинаковой концепции как математического, так и алгоритмического описания вышеупомянутых трансформаций. Идеологически и «чистые» графические API типа OpenGL, и крутые игровые движки типа Unity и Unreal, используют схожие механизмы описания преобразования трехмерной сцены. Не является исключением и OpenSceneGraph.
В этой статье мы сделаем обзор механизмов группировки и трансформации трехмерных объектов в OSG.
1. Матрица модели, матрица вида и матрица проекции
В математическое преобразование координат вовлечены три основных матрицы, осуществляющие трансформацию между различными системами координат. Часто, в терминах OpenGL их называют матрицей модели, матрицей вида и матрицей проекции.
Матрица модели служит для описания расп��ложения объекта в 3D-мире. Она осуществляет преобразование вершин из локальной системы координат объекта в мировую систему координат. К слову, все системы координат в OSG являются правовинтовыми.
Следующим шагом является преобразование мировых координат в пространство вида, выполняемое с помощью матрицы вида. Предположим, что мы имеем камеру, расположенную в начале отсчета мировой системы координат. Матрица, обратная матрице преобразования камеры фактически и используется как матрица вида. В правовинтовой системе координат OpenGL, по-умолчанию, всегда определяет камеру расположенной в точке (0, 0, 0) глобальной системы координат и направленной вдоль отрицательного направления оси Z.
Замечу, что в OpenGL не разделяют понятия матрица модели и матрица вида. Однако, там определяется матрица модель-вид, выполняющая преобразование локальных координат объекта в координаты видового пространства. Эта матрица, по сути, является произведением матрицы модели и матрицы вида. Таким образом, преобразование вершины V из локальных координат в пространство вида можно условно записать как произведение
Ve = V * modelViewMatrix
Следующей важной задачей является определить, как 3D-объекты будут проецироваться в плоскость экрана и вычислить так называемую пирамиду отсечения — область пространства, содержащую объекты, подлежащие отображению на экране. Матрица проекции используется для задания пирамиды отсечения, заданной в мировом пространстве шестью плоскостями: левой, правой, нижней, верхней, ближней и дальней. OpenGL предоставляет функцию gluPerapective(), позволяющую задать пирамиду отсечения и способ проецирования трехмерного мира на плоскость.
Полученная после вышеописанных преобразований система координат называется нормализованной системой координат устройства, имеет по каждой оси диапазон изменения координат от -1 до 1 и является левовинтовой. И, в качестве последнего шага, происходит проецирование полученных данных в порт отображения (вьюпорт) окна, определяемое прямоугольником клиентской области окна. После этого 3D-мир появляется на нашем 2D-экране. Окончательное значение экранных координат вершин Vs можно выразить следующим преобразованием
Vs = V * modelViewMatrix * projectionMatrix * windowMatrix
или
Vs = V * MVPW
где MVPW — эквивалентная матрица преобразования, равная произведению трех матриц: матрицы модель-вид, матрицы проекции и матрицы окна.
Vs в этой ситуации является трехмерным вектором, который определяет положение 2D-пикселя со значением глубины. Обратив операцию преобразования координат мы получим линию в трехмерном пространстве. Поэтому 2D-точку можно рассматривать как две точки — одну на ближней (Zs = 0), другую — на дальней плоскости отсечения (Zs = 1). Координаты этих точек в трехмерном пространстве
V0 = (Xs, Ys, 0) * invMVPW
V1 = (Xs, Ys, 1) * invMVPW
где invMVPW — матрица, обратная MVPW.
Во всех примерах, рассмотренных до сих пор, мы создавали в сценах один единственный трехмерный объект. В этих примерах всегда локальные координаты объекта совпадали с мировыми глобальными координатами. Теперь пришло время поговорит о средствах, позволяющих размещать в сцене множество объектов и менять их положение в пространстве.
2. Групповые ноды
Класс osg::Group представляет собой так называемый групповой узел графа сцены в OSG. Он может иметь любое количество дочерних узлов, включая листовые ноды геометрии или другие групповые узлы. Это наиболее часто используемые узлы, обладающие широкими функциональными возможностями.
Класс osg::Group является производным от класса osg::Node, и соответственно наследуется и от класса osg::Referenced. osg::Group содержит список дочерних нод, где каждая дочерняя нода управляется умным указателем. Это гарантирует отсутствие утечек памяти при каскадном удалении ветки дерева сцены. Данный класс предоставляет разработчику ряд п��бличных методов
- addChild() — присоединяет узел в конец списка дочерних узлов. С другой стороны есть метод insertChild(), помещающий дочерний узел в конкретную позицию списка, которая задается целочисленным индексом или указателем на узел, передаваемыми в качестве параметра.
- removeChild() и removeChildren() — удаление одного узла или группы узлов.
- getChild() — получение указателя на ноду по её индексу в списке
- getNumChildren() — получение числа дочерних узлов, прикрепленных к данной группе.
Управление родительскими узлами
Как мы уже знаем, класс osg::Group управляет группами своих дочерних объектов, среди которых могут присутствовать и экземпляры osg::Geode, управляющие геометрией объектов сцены. Оба упомянутых класса имеют интерфейс для управления родительскими узлами.
OSG позволяет узлам сцены иметь несколько родительских узлов (об этом мы поговорим когда-нибудь потом). Пока же мы рассмотрим методы, определенные в osg::Node, используемые для манипуляций над родительскими узлами:
- getParent() — возвращает указатель типа osg::Group, содержащий перечень родительских узлов.
- getNumParants() — возвращает число родительских узлов.
- getParentalNodePath() — возвращает все возможные пути к корневой ноде сцены от текущей ноды. Он возвращает список переменных типа osg::NodePath.
osg::NodePath представляет собой std::vector указателей на узлы сцены.
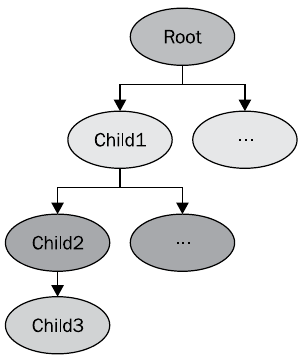
Например, для сцены, изображенной на рисунке следующий код
osg::NodePath &nodePath = child3->getParentalNodePaths()[0];
for (unsigned int i = 0; i < nodePath.size(); ++i)
{
osg::Node *node = nodePath[i];
// Что-нибудь делаем с нодой
}
вернет ноды Root, Child1, Child2.
Вы не должны использовать механизмы управления памятью для ссылки на родительские ноды. При удалении родительской ноды автоматически удаляются и все дочерние ноды, что может привести приложение к краху.
3. Добавление нескольких моделей в дерево сцены
Проиллюстрируем механизм использования групп следующим примером
Полный текст примера group
main.h
main.cpp
#ifndef MAIN_H
#define MAIN_H
#include <osg/Group>
#include <osgDB/ReadFile>
#include <osgViewer/Viewer>
#endif
main.cpp
#include "main.h"
int main(int argc, char *argv[])
{
(void) argc, (void) argv;
osg::ref_ptr<osg::Node> model1 = osgDB::readNodeFile("../data/cessna.osg");
osg::ref_ptr<osg::Node> model2 = osgDB::readNodeFile("../data/cow.osg");
osg::ref_ptr<osg::Group> root = new osg::Group;
root->addChild(model1.get());
root->addChild(model2.get());
osgViewer::Viewer viewer;
viewer.setSceneData(root.get());
return viewer.run();
}
Принципиально пример отличается от всех предыдущих тем, что мы загружаем две трехмерных модели, а для их добавления в сцену создаем групповую ноду root и добавляем в неё наши модельки как дочерние ноды
osg::ref_ptr<osg::Group> root = new osg::Group;
root->addChild(model1.get());
root->addChild(model2.get());

В итоге мы получаем сцену, состоящую из двух моделей — самолета и смешной зеркальной коровы. Кстати, зеркальная корова не будет зеркальной, если не скопировать её текстуру из OpenSceneGraph-Data/Images/reflect.rgb а каталог data/Images нашего проекта.
Класс osg::Group может принимать в качестве дочерних любые типы узлов, в том числе и узлы своего типа. Напротив, класс osg::Geode не содержит вообще каких-либо дочерних узлов — он является оконечным узлом, содержащим в себе геометрию объекта сцены. Этот факт удобен при выяснении вопроса является ли узел узлом типа osg::Group или другого типа производного от osg::Node. Рассмотрим маленький пример
osg::ref_ptr<osg::Group> model = dynamic_cast<osg::Group *>(osgDB::readNodeFile("../data/cessna.osg"));
Значение, возвращаемое функцией osgDB::readNodeFile() всегда имеет тип osg::Node*, но оно может быть преобразовано к своему наследнику osg::Group*. Если коневой узел модели Cessna это групповой узел, то преобразование будет успешным, в противном случае преобразование вернет NULL.
Можно выполнить так же такой фокус, работающий на большинстве компиляторов
// Загружаем модель в групповой узел
osg::ref_ptr<osg::Group> group = ...;
// Преобразуем его к узлу
osg::Node* node1 = dynamic_cast<osg::Node*>( group.get() );
// Преобразуем группу к узлу неявно
osg::Node* node2 = group.get();
В критических для производительности местах кода лучше использовать специальные методы преобразования
osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("cessna.osg");
osg::Group* convModel1 = model->asGroup(); // Работает нормально
osg::Geode* convModel2 = model->asGeode(); // Вернет NULL.
4. Ноды трансформации
Узлы osg::Group не могут делать никаких преобразований, кроме возможности перехода к своим дочерним узлам. Для пространственного перемещения геометрии OSG предоставляет класс osg::Transform. Этот класс является наследником класса osg::Group, но и сам является абстрактным — на практике вместо него применяются его наследники, реализующие различные пространственные преобразования геометрии. При обходе графа сцены узел osg::Transform добавляет свое преобразование в текущую матрицу преобразования OpenGL. Это эквивалентно перемножению матриц преобразования OpenGL, выполняемое командой glMultMatrix()
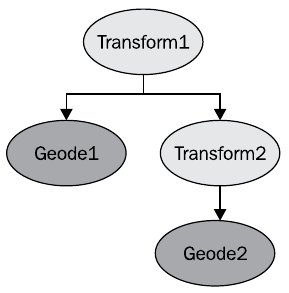
Этот пример графа сцены можно транслировать в следующий кода на OpenGL
glPushMatrix();
glMultMatrix( matrixOfTransform1 );
renderGeode1();
glPushMatrix();
glMultMatrix( matrixOfTransform2 );
renderGeode2();
glPopMatrix();
glPopMatrix();
Можно сказать, что положение Geode1 задается в системе координат Transform1, а положение Geode2 задается в системе координат Transform2, смещенной относительно Transform1. При этом в OSG можно включить позиционирование в абсолютных координатах, что приведет к поведению объекта, эквивалентному результату команды glGlobalMatrix() OpenGL
transformNode->setReferenceFrame( osg::Transform::ABSOLUTE_RF );
Можно переключится обратно в режим позиционирования относительными координатами
transformNode->setReferenceFrame( osg::Transform::RELATIVE_RF );
5. Понятие о матрице преобразования координат
Тип osg::Matrix это базовый тип OSG не управляемый умными указателями. Он предоставляет интерфейс к операциями над матрицами размерности 4х4, описывающими преобразование координат, таких как перемещение, поворот, масштабирование и вычисление проекций. Матрица может быть задана явно
// Единичная матрица 4х4
osg::Matrix mat(1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f );
Класс osg::Matrix предоставляет следующие публичные методы:
- postMult() и operator* () — умножение справа текущей матрицы на матрицу или вектор, переданные в качестве параметра. Метод preMult() выполняет умножение слева.
- makeTranslate(), makeRotate() и makeScale() — сбрасывают текущую матрицу и создают матрицу 4х4 описывающую перемещение, вращение и масштабирование. их статические версии translate(), rotate() и scale() могут быть использованы для создания матричного объекта со специфическими параметрами.
- invert() — вычисление матрицы обратной текущей. Его статическая версия inverse() принимает в качестве параметра матрицу и возвращает новую матрицу, обратную данной.
OSG понимает матрицы как матрицы строк, а векторы как строки, поэтому для применения к вектору матричного преобразования следует поступать так
osg::Matrix mat = …;
osg::Vec3 vec = …;
osg::Vec3 resultVec = vec * mat;
Порядок матричных операций легко понять, посмотрев как перемножаются матрицы для получения эквивалетного преобразования
osg::Matrix mat1 = osg::Matrix::scale(sx, sy, sz);
osg::Matrix mat2 = osg::Matrix::translate(x, y, z);
osg::Matrix resultMat = mat1 * mat2;
Разработчик должен читать процесс трансформации слева направо. То есть, в описанном фрагменте кода сначала происходит масштабирование вектора, а затем его перемещение.
osg::Matrixf содержит элементы типа float.
6. Применение класса osg::MatrixTransform
Применим полученные теоретические знания на практике, загрузив две модели самолета в разные точки сцены.
Полный текст примера transform
main.h
main.cpp
#ifndef MAIN_H
#define MAIN_H
#include <osg/MatrixTransform>
#include <osgDB/ReadFile>
#include <osgViewer/Viewer>
#endif
main.cpp
#include "main.h"
int main(int argc, char *argv[])
{
(void) argc; (void) argv;
osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg");
osg::ref_ptr<osg::MatrixTransform> transform1 = new osg::MatrixTransform;
transform1->setMatrix(osg::Matrix::translate(-25.0, 0.0, 0.0));
transform1->addChild(model.get());
osg::ref_ptr<osg::MatrixTransform> transform2 = new osg::MatrixTransform;
transform2->setMatrix(osg::Matrix::translate(25.0, 0.0, 0.0));
transform2->addChild(model.get());
osg::ref_ptr<osg::Group> root = new osg::Group;
root->addChild(transform1.get());
root->addChild(transform2.get());
osgViewer::Viewer viewer;
viewer.setSceneData(root.get());
return viewer.run();
}
Пример, на самом деле довольно тривиален. Загружаем модель самолета из файла
osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg");
Создаем ноду трансформации
osg::ref_ptr<osg::MatrixTransform> transform1 = new osg::MatrixTransform;
Устанавливаем в качестве матрицы преобразования перемещение модели по оси X на 25 единиц влево
transform1->setMatrix(osg::Matrix::translate(-25.0, 0.0, 0.0));
Задаем для ноды трансформации нашу модель в качестве дочернего узла
transform1->addChild(model.get());
Аналогично поступаем и со второй трансформацией, но в качестве матрица задаем перемещение вправо на 25 единиц
osg::ref_ptr<osg::MatrixTransform> transform2 = new osg::MatrixTransform;
transform2->setMatrix(osg::Matrix::translate(25.0, 0.0, 0.0));
transform2->addChild(model.get());
Создаем корневую ноду и в качестве дочерних узлов для неё задаем трансформационные ноды transform1 и transform2
osg::ref_ptr<osg::Group> root = new osg::Group;
root->addChild(transform1.get());
root->addChild(transform2.get());
Создаем вьювер и в качестве данных сцены передаем ему корневую ноду
osgViewer::Viewer viewer;
viewer.setSceneData(root.get());
Запуск программы дает такую картинку

Структура графа сцены в этом примере такова
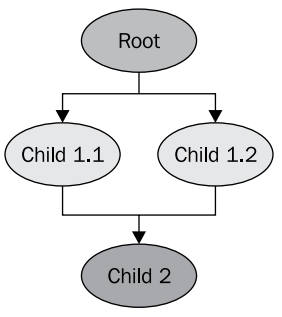
Нас не должен смущать тот факт, что ноды трансформации (Child 1.1 и Child 1.2) ссылаются на один и тот же дочерний объект модели самолета (Child 2). Это штатный механизм OSG, когда один дочерний узел графа сцены может иметь несколько родительских узлов. Таким образом нам не обязательно хранить в памяти два экземпляра модели, чтобы получить в сцене два одинаковых самолета. Такой механизм позволяет очень эффективно распределять память в приложении. Модель не будет удалена из памяти, пока на неё ссылается, как на дочернюю, хотя бы одна нода.
По своему действию класс osg::MatrixTransform эквивалентен командам OpenGL glMultMatrix() и glLoadMatrix(), реализует все виды пространственных преобразований, но сложен в использованию из-за необходимости вычислять матрицу преобразования.
Класс osg::PositionAttitudeTransform работает как функции OpenGL glTranslate(), glScale(), glRotate(). Он предоставляет публичные методы для преобразования дочерних узлов:
- setPosition() — переместить узел в данную точку пространства, задаваемую параметром osg::Vec3
- setScale() — масштабировать объект по осям координат. Коэффициенты масштабирования по соответствующим осям задаются параметром типа osg::Vec3
- setAttitude() — задать пространственную ориентацию объекта. В качестве параметра принимает кватернион преобразования поворота osg::Quat, конструктор которого имеет несколько перегрузок, позволяющих задавать кватернион как непосредственно (покомпонентно), так и, например, через углы Эйлера osg::Quat(xAngle, osg::X_AXIS, yAngle, osg::Y_AXIS, zAngle, osg::Z_AXIS) (углы задаются в радианах!)
7. Ноды-переключатели
Рассмотрим еще один класс — osg::Switch, позволяющий отображать или пропускать рендеринг узла сцены, в зависимости от некоего логического условия. Он является наследником класса osg::Group и прикрепляет к каждой своей дочерней ноде некоторое логическое значение. Он имеет несколько полезных публичных методов:
- Перегруженный addChild(), в качестве второго параметра принимающий логический ключ, указывающий отображать или нет данный узел.
- setValue() — установка ключа видимости/невидимости. Принимает индекс интересующей нас дочерней ноды и желаемое значение ключа. Соответственно getValue() позволяет получить текущее значение ключа по индексу интересующей нас ноды.
- setNewChildDefaultValue() — установка значения по-умолчанию для ключа видимости всех новых объектов, добавляемых в качестве дочерних.
Рассмотрим применение данного класса на примере.
Полный текст примера switch
main.h
main.cpp
#ifndef MAIN_H
#define MAIN_H
#include <osg/Switch>
#include <osgDB/ReadFile>
#include <osgViewer/Viewer>
#endif
main.cpp
#include "main.h"
int main(int argc, char *argv[])
{
(void) argc; (void) argv;
osg::ref_ptr<osg::Node> model1 = osgDB::readNodeFile("../data/cessna.osg");
osg::ref_ptr<osg::Node> model2 = osgDB::readNodeFile("../data/cessnafire.osg");
osg::ref_ptr<osg::Switch> root = new osg::Switch;
root->addChild(model1.get(), false);
root->addChild(model2.get(), true);
osgViewer::Viewer viewer;
viewer.setSceneData(root.get());
return viewer.run();
}
Пример тривиален — мы загружаем две модели: обычную цессну и цессну с эффектом горящего двигателя
osg::ref_ptr<osg::Node> model1 = osgDB::readNodeFile("../data/cessna.osg");
osg::ref_ptr<osg::Node> model2 = osgDB::readNodeFile("../data/cessnafire.osg");
Однако, в качестве корневой ноды создаем osg::Switch, что позволяет нам, при добавлении в неё моделей в качестве дочерних узлов задать ключ видимости для каждой из них
osg::ref_ptr<osg::Switch> root = new osg::Switch;
root->addChild(model1.get(), false);
root->addChild(model2.get(), true);
То есть, model1 не будет рендерится, а model2 будет, что мы и пронаблюдаем, запустив программу

Поменяв местами значения ключей будем видеть противоположную картину
root->addChild(model1.get(), true);
root->addChild(model2.get(), false);

Взведя оба ключа, увидим две модели одновременно
root->addChild(model1.get(), true);
root->addChild(model2.get(), true);

Включать видимость и невидимость ноды, дочерней для osg::Switch можно прямо на ходу, используя метод setValue()
switchNode->setValue(0, false);
switchNode->setValue(0, true);
switchNode->setValue(1, true);
switchNode->setValue(1, false);
Заключение
В этом уроке мы рассмотрели все основные классы промежуточных узлов, используемых в OpenSceeneGraph. Таким образом мы уложили ещё один базовый кирпич в фундамент знаний об устройстве этого несомненно интересного графического движка. Рассмотренные в статье примеры, как и ранее, доступны в моем репозитории на Github.
Продолжение следует...