Существует ряд задач, в которых длительный по времени сигнал разбивается на сегменты, каждый из которых обрабатывается по отдельности. В частности, такой подход используется для анализа сигнала с помощью оконного преобразования Фурье, или наоборот, при синтезе; а также при спектральной обработке типа удаления шума, изменения темпа, нелинейной фильтрации, сжатии аудиоданных и других.
Сам процесс разбиения математически представляется умножением на некоторую весовую (оконную) функцию со смещением. Для самого простого окна — прямоугольного — это может выглядеть так:
Исходный сигнал:
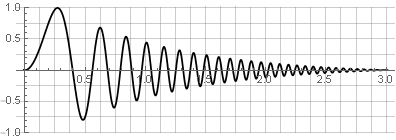
Разбиения:
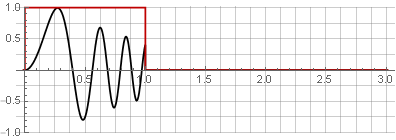
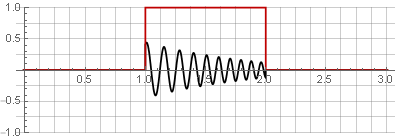
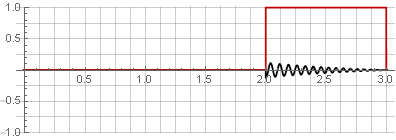
Можно восстановить исходный сигнал, просто просуммировав их.
Однако по ряду причин прямоугольная функция — не самая лучшая оконная функция. При спектральном анализе через (обычно быстрое) дискретное преобразование Фурье анализируемый блок данных как бы «зацикливается», что приводит к разрыву на краях и искажению спектра:
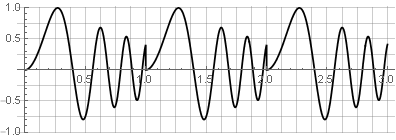
Не является оно подходящим и для обратного синтеза — поскольку любое изменение также приведёт к разрывам — например, если мы попробуем реверсировать одну из частей:

Для устранения этих недостатков используется перекрытие — когда каждое следующее окно захватывает часть данных из предыдущего; а весовое окно, соответственно, плавно спадает к краям.
Наиболее часто для этого используют окно Ханна (известное также под названием «приподнятый косинус») с перекрытием на 50%:

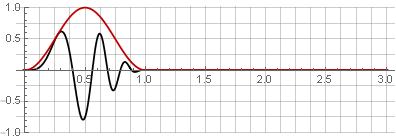

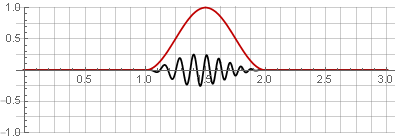
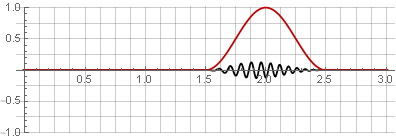

За счёт симметричности функции косинуса при сложении они суммируются в единицу:
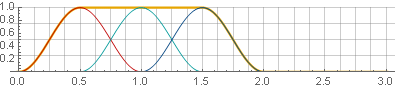
Теперь при обратном синтезе мы не получим разрывов — но только при условии, что на границах окна значения по-прежнему будут уходить в ноль. Например, при реверсировании одной из частей гладкость не нарушится:
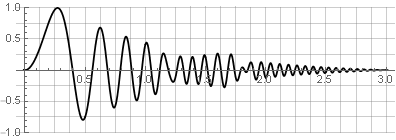
Рассмотрим более подробно алгоритм для обработки сигнала с использованием быстрого преобразования Фурье (FFT):
При этом, если обработку спектра не производить, сигнал на выходе должен быть идентичен сигналу на входе (только с неизбежной задержкой во времени).
При использовании окна Ханна перекрытия на 50% уже недостаточно, так как будут возникать провалы:

Поскольку двойное наложение равносильно возведению в квадрат, то очевидным решением будет использовать корень из окна Ханна, чтобы компенсировать возведение в квадрат:
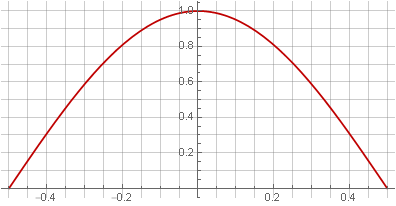
В этом случае, правда, окно перестало быть гладким на краях — появился разрыв в первой производной.
Можно пойти и другим путём — использовать перекрытие на 75%, и тогда окна также будут суммироваться в константу — только уже не в , а в
, а в  :
:
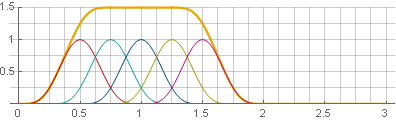
В данном случае нам просто повезло. Если разложить квадрат на сумму — то можно увидеть, что оно представляет собой композицию из двух окон Ханна, но в разных масштабах, что и позволяет выполнять необходимые нам требования:

С другими оконными функциями такой фокус не пройдёт; также далеко не все стандартные оконные функции могут обеспечить суммирование в константу и при 50% перекрытии.
Можно рассматривать окно Ханна не как самостоятельную функцию, а как разницу двух кусочно-непрерывных функций (подробному рассмотрению которых была посвящена отдельная статья) со смещением. Например, используя следующую функцию

можно записать
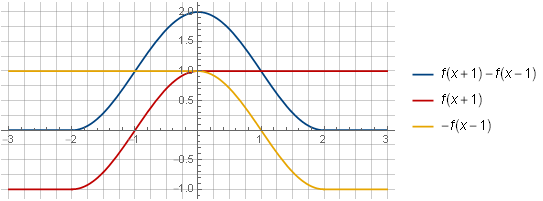
Рассмотрев компоненты суммы двух таких окон, их способность суммироваться в константу станет более наглядным:
На отрезке![$[0,2]$](https://habrastorage.org/getpro/habr/formulas/b88/1a6/0a9/b881a60a94c627adb61b4a4bc375ec3a.svg) мы получили взаимную компенсацию при сложении функций
мы получили взаимную компенсацию при сложении функций  и
и  , поскольку
, поскольку 
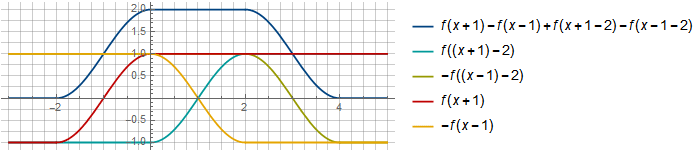
Можно выбрать и другое смещение, с большим перекрытием, например:

И тогда, при смещении с шагом , они также будут суммироваться в константу:
, они также будут суммироваться в константу:

Видно, что если перегруппировать компоненты оконной функции, то получатся всё те же окна Ханна.
Таким образом, используя разные функции ограничения, можно формировать окна необходимой формы.
Теперь осталось только задать масштаб, чтобы области определения и значения не зависели от величины перекрытия. Определив окно на интервале![$[0,1]$](https://habrastorage.org/getpro/habr/formulas/6e2/075/7f0/6e20757f072cd273db5f1ea44424f67d.svg) получим
получим
где — кусочно-непрерывная функция вида
— кусочно-непрерывная функция вида
а — некоторая интерполирующая функция между точками
— некоторая интерполирующая функция между точками  и
и  .
.
Параметр определяет уровень перекрытия — делитель, определяющий шаг, на который необходимо смещать каждое следующее окно,
определяет уровень перекрытия — делитель, определяющий шаг, на который необходимо смещать каждое следующее окно,  , и должен быть больше единицы,
, и должен быть больше единицы,  .
.
Процент перекрытия можно посчитать по формуле
можно посчитать по формуле
и соответственно наоборот
Итоговый вид окна будет зависеть как от выбора уровня перекрытия, так и от выбора ограничивающей функции.
Здесь мы рассмотрим несколько готовых решений, ради которых всё и затевалось. Для простоты будем рассматривать просто интерполирующую функцию , без всякой прочей обвязки.
, без всякой прочей обвязки.
Являются наименее вычислительно затратными. Используя ранее выведенную формулу
получим полином с заданным количеством нулей на высших производных, обеспечивающих необходимую гладкость окна на краях.
С перекрытием на 75% окна с различными значениями n окна будут выглядеть так:
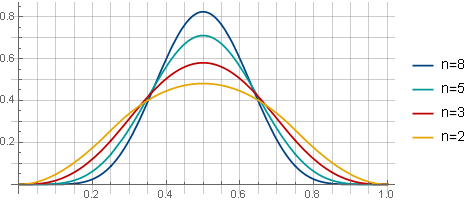
А в случае с извлечением корня — так (при использовании 75% перекрытия):

или так (при использовании 50% перекрытия):

Функция
интересна тем, что бесконечно дифференцируема и все её производные на краях равны 0 (что можно доказать, рассмотрев её производные исходя из правил дифференцирования — в каждом слагаемом будет обнуляющий его множитель). Это позволяет на её основе строить окна, все производных которых не имеют разрывов:

Необходимость такого вида окна вызвана тем, чтобы увеличить разрешение FFT, но снизить влияние эффекта «частотно-временной неопределённости» на высоких частотах за счёт увеличения их концентрации в центре.
Сначала определим желаемый вид оконной функции — например, следующим образом:
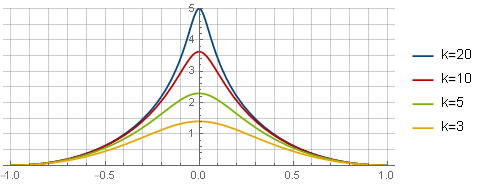
Здесь первое слагаемое определяет сам вид функции, второе — обеспечивает пересечение с осью абсцисс, третье (парабола) обнуляет производную на краях для гладкой стыковки; а параметр определяет «остроту» вершины. В таком виде она ещё не пригодна для использования — сначала из неё нужно получить функцию ограничения посредством интегрирования и масштабирования:
определяет «остроту» вершины. В таком виде она ещё не пригодна для использования — сначала из неё нужно получить функцию ограничения посредством интегрирования и масштабирования:
Для удобства настройки можно привязать параметр к уровню перекрытия
к уровню перекрытия  — например, таким образом, чтобы 4-ая производная в центре окна была равна 0 — и тогда
— например, таким образом, чтобы 4-ая производная в центре окна была равна 0 — и тогда  будет считаться как
будет считаться как :
:
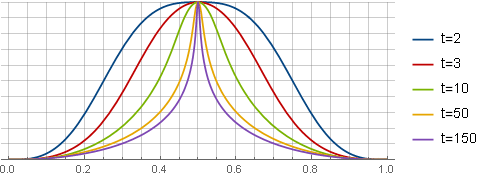
Здесь для наглядности все окна приведены к одному масштабу.
Представляет из себя более «агрессивный» вариант предыдущего окна. В качестве основы была выбрана гипербола, из которой путём последовательных трансформаций
и использования тех же шагов в виде интегрирования и масштабирования получили формулу
Здесь также можно привязать параметр к уровню перекрытия. Непосредственное решение уравнения 4-ой производной даёт слишком громоздкий результат, поэтому просто сделаем по образу и подобию из решения для предыдущего окна, определив
к уровню перекрытия. Непосредственное решение уравнения 4-ой производной даёт слишком громоздкий результат, поэтому просто сделаем по образу и подобию из решения для предыдущего окна, определив  как
как  , обеспечив таким образом роль параметра
, обеспечив таким образом роль параметра  как «тонкая настройка». При
как «тонкая настройка». При  окна будут выглядеть следующим образом:
окна будут выглядеть следующим образом:
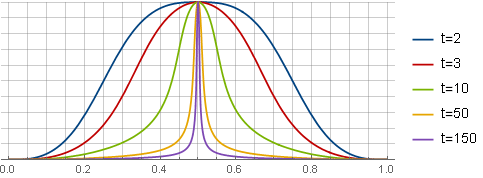
Оконная функция совсем не обязательно должна быть симметричной. Допустим, нам требуется окно с резкой атакой и плавным затуханием. Мы можем получить его по уже знакомой схеме — сначала определить желаемый вид функции, а затем интегрированием получить функцию ограничения. Здесь задача слегка усложняется за счёт того, что из-за асимметрии центр уже не будет проходить через начало координат, поэтому добавляется дополнительный шаг вычислений. Это также приводит к тому, что формулы в результате получаются довольно громоздкими. Для примера рассмотрим простейший вариант — параболу, умноженную на полиномиальное весовое окно:

Здесь степень при x в веcовом окне (а именно 10) определяет «резкость» атаки. Мы использовали конкретное значение, а не символьный параметр, чтобы упростить формулы для наглядности — при желании, в дальнейшем его можно пересчитать.
После интегрирования просто масштабирования уже недостаточно — нужно ещё выровнять края:

Для этого мы сначала сместим функцию наверх, чтобы выровнять левый край, а затем масштабируем к двойке по правому краю и вычтем единицу. После чего получим следующую формулу:
Для того, чтобы итоговое окно имело желаемый вид, нужно также обеспечить достаточное большой уровень перекрытия:

Аналогичным образом можно строить окна и из любых других колоколообразных функций — например, гауссианы; а также можно модифицировать уже рассмотренные для обеспечения большей гладкости или изменения формы кривой.
Вне рассмотрения остался спектральный состав таких оконных функций — этому нужно посвящать отдельные исследования.
Чуть более расширенный вариант статьи (с возможностью динамического изменения параметров в рассматриваемых окнах и скрытыми формулами) в виде документа Wolfram Mathematica можно скачать здесь.
Сам процесс разбиения математически представляется умножением на некоторую весовую (оконную) функцию со смещением. Для самого простого окна — прямоугольного — это может выглядеть так:
Исходный сигнал:

Разбиения:



Можно восстановить исходный сигнал, просто просуммировав их.
Подробнее
Однако по ряду причин прямоугольная функция — не самая лучшая оконная функция. При спектральном анализе через (обычно быстрое) дискретное преобразование Фурье анализируемый блок данных как бы «зацикливается», что приводит к разрыву на краях и искажению спектра:

Не является оно подходящим и для обратного синтеза — поскольку любое изменение также приведёт к разрывам — например, если мы попробуем реверсировать одну из частей:

Для устранения этих недостатков используется перекрытие — когда каждое следующее окно захватывает часть данных из предыдущего; а весовое окно, соответственно, плавно спадает к краям.
Перекрытие на 50%
Наиболее часто для этого используют окно Ханна (известное также под названием «приподнятый косинус») с перекрытием на 50%:






За счёт симметричности функции косинуса при сложении они суммируются в единицу:

Теперь при обратном синтезе мы не получим разрывов — но только при условии, что на границах окна значения по-прежнему будут уходить в ноль. Например, при реверсировании одной из частей гладкость не нарушится:

Обработка с двойным наложением окон
Рассмотрим более подробно алгоритм для обработки сигнала с использованием быстрого преобразования Фурье (FFT):
- разбиение сигнала на сегменты с наложением окна;
- прямое FFT;
- обработка спектра;
- обратное FFT;
- повторное наложение окна (поскольку после обратного FFT границы не обязательно будут стыковаться с нулём без разрыва);
- суммирование результирующих сегментов.
При этом, если обработку спектра не производить, сигнал на выходе должен быть идентичен сигналу на входе (только с неизбежной задержкой во времени).
При использовании окна Ханна перекрытия на 50% уже недостаточно, так как будут возникать провалы:

Поскольку двойное наложение равносильно возведению в квадрат, то очевидным решением будет использовать корень из окна Ханна, чтобы компенсировать возведение в квадрат:

В этом случае, правда, окно перестало быть гладким на краях — появился разрыв в первой производной.
Примечание
Интересно, что в данном случае у нас получилась половина периода синусоиды.
Можно пойти и другим путём — использовать перекрытие на 75%, и тогда окна также будут суммироваться в константу — только уже не в

В данном случае нам просто повезло. Если разложить квадрат на сумму — то можно увидеть, что оно представляет собой композицию из двух окон Ханна, но в разных масштабах, что и позволяет выполнять необходимые нам требования:

С другими оконными функциями такой фокус не пройдёт; также далеко не все стандартные оконные функции могут обеспечить суммирование в константу и при 50% перекрытии.
Идея
Можно рассматривать окно Ханна не как самостоятельную функцию, а как разницу двух кусочно-непрерывных функций (подробному рассмотрению которых была посвящена отдельная статья) со смещением. Например, используя следующую функцию

можно записать

Рассмотрев компоненты суммы двух таких окон, их способность суммироваться в константу станет более наглядным:

На отрезке
Можно выбрать и другое смещение, с большим перекрытием, например:

И тогда, при смещении с шагом

Видно, что если перегруппировать компоненты оконной функции, то получатся всё те же окна Ханна.
Таким образом, используя разные функции ограничения, можно формировать окна необходимой формы.
Итоговая формула
Теперь осталось только задать масштаб, чтобы области определения и значения не зависели от величины перекрытия. Определив окно на интервале
где
а
Параметр
Процент перекрытия
и соответственно наоборот
Примечание
При работе с реальными данными может потребоваться пересчёт уровня перекрытия в зависимости от конкретного размера FFT. Например, при FFT на 2048 точек и уровнем перекрытия 3 получаем шаг 2048/3=682.666..., что на практике, естественно, нереализуемо. Поэтому округлим его до целого, а  пересчитаем как 2048/683=2.998535871156662…
пересчитаем как 2048/683=2.998535871156662…
Либо же можно наоборот — использовать размер окна, заведомо делящийся на 3 (скажем, 999), а остаток до необходимого размера для FFT дополнить нулями (25-ю).
Либо же можно наоборот — использовать размер окна, заведомо делящийся на 3 (скажем, 999), а остаток до необходимого размера для FFT дополнить нулями (25-ю).
Итоговый вид окна будет зависеть как от выбора уровня перекрытия, так и от выбора ограничивающей функции.
Несколько интересных примеров
Здесь мы рассмотрим несколько готовых решений, ради которых всё и затевалось. Для простоты будем рассматривать просто интерполирующую функцию
Полиномиальные окна
Являются наименее вычислительно затратными. Используя ранее выведенную формулу
получим полином с заданным количеством нулей на высших производных, обеспечивающих необходимую гладкость окна на краях.
первые 10 полиномов
С перекрытием на 75% окна с различными значениями n окна будут выглядеть так:

А в случае с извлечением корня — так (при использовании 75% перекрытия):

или так (при использовании 50% перекрытия):

Максимально гладкое окно
Функция
интересна тем, что бесконечно дифференцируема и все её производные на краях равны 0 (что можно доказать, рассмотрев её производные исходя из правил дифференцирования — в каждом слагаемом будет обнуляющий его множитель). Это позволяет на её основе строить окна, все производных которых не имеют разрывов:

Окно вида «юбочка»
Необходимость такого вида окна вызвана тем, чтобы увеличить разрешение FFT, но снизить влияние эффекта «частотно-временной неопределённости» на высоких частотах за счёт увеличения их концентрации в центре.
Сначала определим желаемый вид оконной функции — например, следующим образом:

Здесь первое слагаемое определяет сам вид функции, второе — обеспечивает пересечение с осью абсцисс, третье (парабола) обнуляет производную на краях для гладкой стыковки; а параметр
Для удобства настройки можно привязать параметр

Здесь для наглядности все окна приведены к одному масштабу.
Окно вида «иголка»
Представляет из себя более «агрессивный» вариант предыдущего окна. В качестве основы была выбрана гипербола, из которой путём последовательных трансформаций
и использования тех же шагов в виде интегрирования и масштабирования получили формулу
Здесь также можно привязать параметр

Асимметричное окно
Оконная функция совсем не обязательно должна быть симметричной. Допустим, нам требуется окно с резкой атакой и плавным затуханием. Мы можем получить его по уже знакомой схеме — сначала определить желаемый вид функции, а затем интегрированием получить функцию ограничения. Здесь задача слегка усложняется за счёт того, что из-за асимметрии центр уже не будет проходить через начало координат, поэтому добавляется дополнительный шаг вычислений. Это также приводит к тому, что формулы в результате получаются довольно громоздкими. Для примера рассмотрим простейший вариант — параболу, умноженную на полиномиальное весовое окно:

Здесь степень при x в веcовом окне (а именно 10) определяет «резкость» атаки. Мы использовали конкретное значение, а не символьный параметр, чтобы упростить формулы для наглядности — при желании, в дальнейшем его можно пересчитать.
После интегрирования просто масштабирования уже недостаточно — нужно ещё выровнять края:

Для этого мы сначала сместим функцию наверх, чтобы выровнять левый край, а затем масштабируем к двойке по правому краю и вычтем единицу. После чего получим следующую формулу:
Для того, чтобы итоговое окно имело желаемый вид, нужно также обеспечить достаточное большой уровень перекрытия:

Заключение
Аналогичным образом можно строить окна и из любых других колоколообразных функций — например, гауссианы; а также можно модифицировать уже рассмотренные для обеспечения большей гладкости или изменения формы кривой.
Вне рассмотрения остался спектральный состав таких оконных функций — этому нужно посвящать отдельные исследования.
Чуть более расширенный вариант статьи (с возможностью динамического изменения параметров в рассматриваемых окнах и скрытыми формулами) в виде документа Wolfram Mathematica можно скачать здесь.