Всем привет! Разработка гексапода продвигается и наконец-то базовая математическая часть протестирована и готова к документированию. Чтобы проект дожил до конца и не остался пылиться на полке нужно видеть его сдвиги в положительную сторону, даже если они незначительны. В этой статье я расскажу об алгоритме решения обратной задачи кинематики и наглядно покажу его в действии. Надеюсь будет интересно.

Этапы разработки:
Часть 1 — проектирование
Часть 2 — сборка
Часть 3 — кинематика
Часть 4 — математика траекторий и последовательности
Часть 5 — электроника
Часть 6 — переход на 3D печать
Часть 7 — новый корпус, прикладное ПО и протоколы общения
Часть 8 — улучшенная математика передвижения
Часть 9 — завершение версии 1.00

Системы координат


Для начала стоит определится с системами координат робота — их аж целых три:

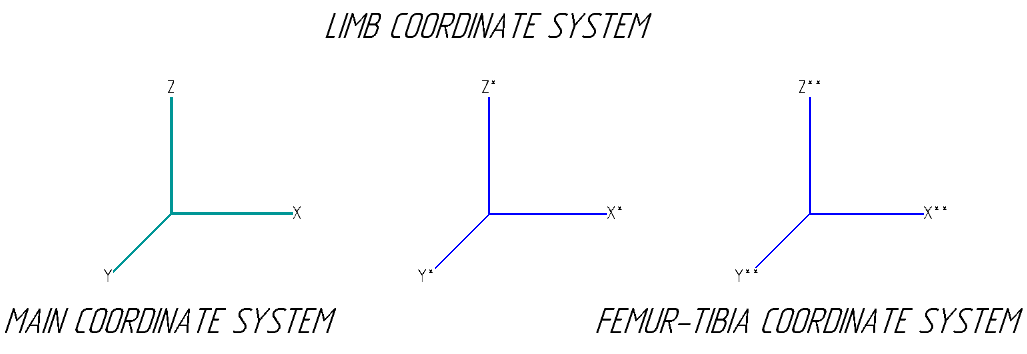
По сути они ни чем друг от друга не отличаются, но располагаются в разных местах корпуса и могут быть повернуты относительно друг друга на какой-то угол. При виде сверху расположение осей будет следующим (параметр coxa_zero_rotate будет описан чуть позже):


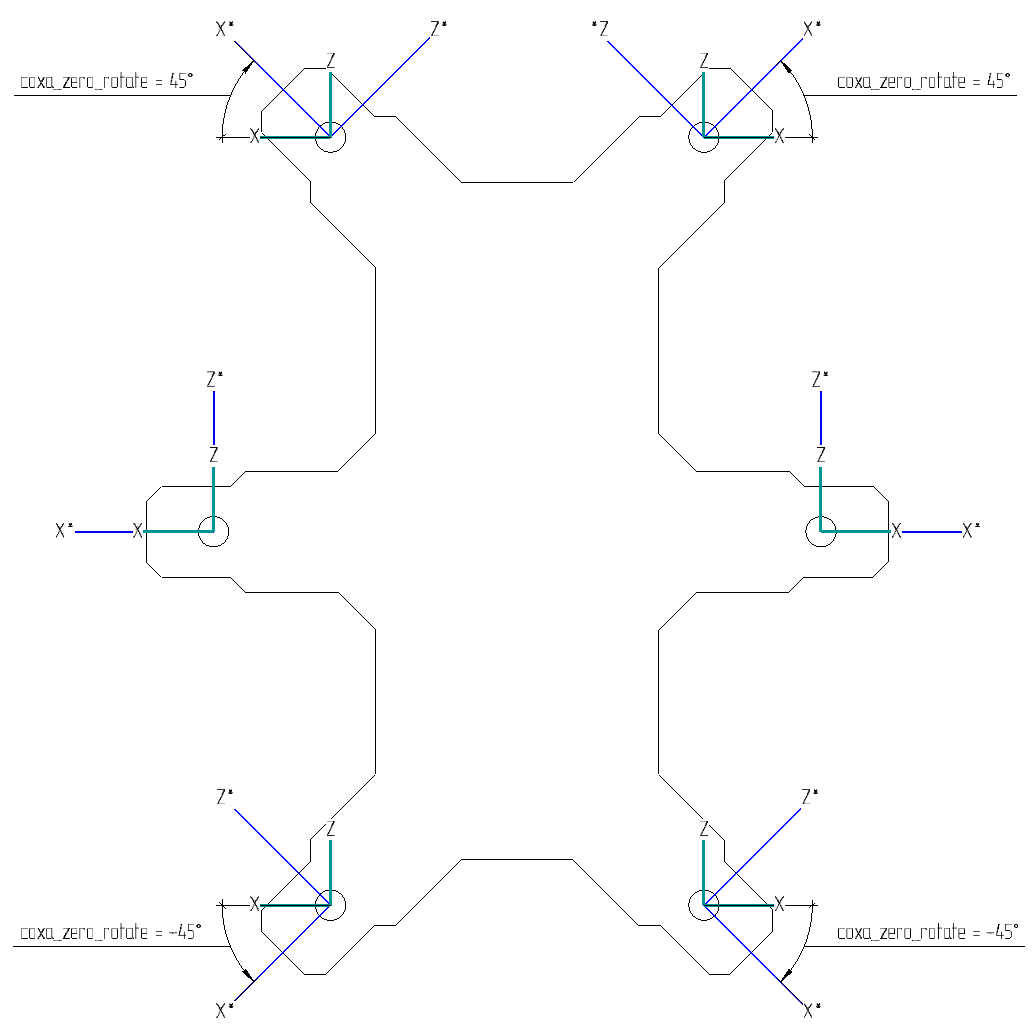
Как вы уже наверно заметили, системы координат на левой и правой сторонах расположены симметрично относительно центра ко��пуса. Мне показалось, что так будет проще.

Координаты каждой точки задаются относительно той конечности, для которой эта точка предназначена. Такой подход позволит безболезненно перемещать конечность куда угодно не вмешиваясь в конфигурацию.

А вот так они расположены относительно конечности:


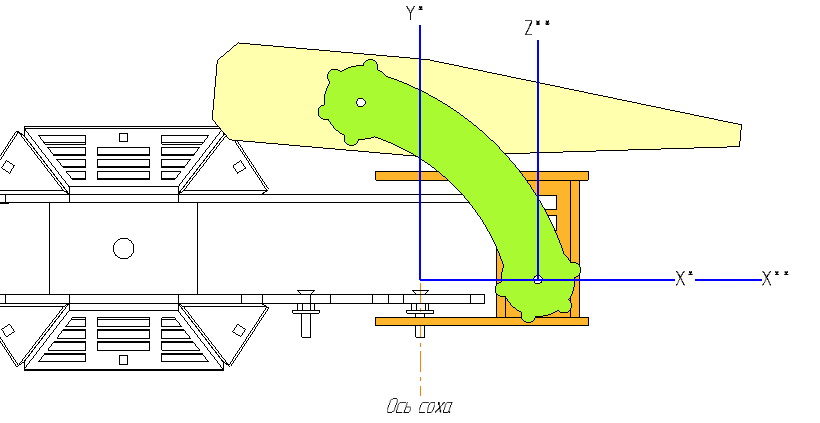
Координаты целевой точки задаются относительно MAIN COORDINATE SYSTEM. Изначально я хотел задавать координаты относительно центра корпуса, но это оказалось не очень удобно и требовало хранения ряда дополнительных параметров.

Далее по тексту обозначения X*, X** и т.д. будут заменены на X′, X′′.

Решение обратной задачи кинематики


Начнем с самого сложного и интересного для меня момента — кинематики. Алгоритм я придумывал сам, иногда поглядывая на свойства треугольника и тригонометрические функции. С механикой у меня тяжко, а с тригонометрией еще хуже, так что возможно я где-то что-то мог не учесть, но этот алгоритм работает (видео в конце).

1. Постановка задачи


Допустим нам нужно, чтобы передняя правая конечность дотянулась до точки А с координатами (150; -20; 100). Так же известно, что конечность повернута относительно корпуса на 45 градусов (параметр coxa_zero_rotate):


Сама конечность имеет следующие параметры:


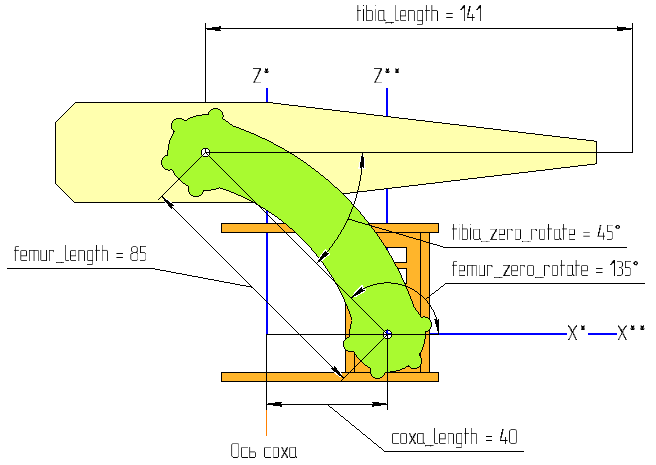
Я думаю не нужно описывать что эти параметры значат, названия говорят сами за себя. Можно добавить только то, что эти все параметры определяются конфигурацией корпуса, являются постоянными и хранятся во FLASH памяти с возможностью редактирования из вне (для гибкости).

Вот зачем это нужно

На картинке представлены различные вариации корпусов и расположения ног гексапода. Сейчас он соответствует конфигурации ARACNID. Предположим мне в голову стукнуло поменять корпус на REPTILES и для этого будет достаточно просто поменять значения параметров без измерения в самой программе, даже целевые точки менять не придется (если конечно грамотно подойти к этому).

Всех представленных выше параметров достаточно для решения поставленной задачи.

2. Решение задачи


2.1 Нахождение угла поворота COXA

Данный этап является самым простым. Для начала необходимо пересчитать координаты точки А относительно LIMB COORDINATE SYSTEM. Очевидно, что нужно выполнить поворот на угол coxa_zero_rotate, сделать это можно используя следующие формулы:

$x′ = x ⋅ cos(α) + z ⋅ sin(α) = 150 ⋅ cos(45) + 100 ⋅ sin(45) = 176.78$


$y′ = y = -20$


$z′ = -x ⋅ sin(α) + z ⋅ cos(α) = -150 ⋅ sin(45) + 100 ⋅ cos(45) = -35.36$


Таким образом мы получили координаты целевой точки А (176.78; -20; -35.36) относительно LIMB COORDINATE SYSTEM.

Теперь можно найти угол COXA используя функцию atan2:

$COXA = atan2(z′, x′) = atan2(-35.36, 176.78) = -11.30°$


И так, мы получили угол, на который нужно повернуть сервопривод COXA, чтобы точка А находилась в плоскости X′Y′. Давайте теперь проверим наши расчеты в КОМПАС 3D:


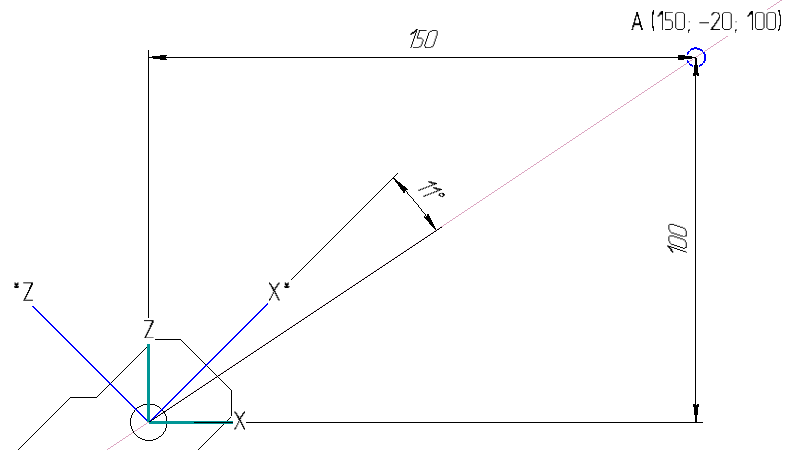
Все верно.

2.2 Нахождение угла поворота FEMUR и TIBIA
Для нахождения этих углов необходимо перейти к плоскости X′Y′. Для перехода к плоскости нужно выполнить поворот точки на угол COXA, который мы уже рассчитали ранее.

$x′ = x′ ⋅ cos(α) + y′ ⋅ sin(α) = 176.78 ⋅ cos(-11) + -20 ⋅ sin(-11) = 180.28$


$y′ = y = -20$


Координата y′ не меняется, так как мы выполняем поворот по оси Y′.

Дальше нужно убрать из расчета длину COXA, т.е. перейдем к плоскости X′′Y′′, для этого выполним сдвиг координаты x′ точки на длину COXA:

$x′′ = x′ - coxaLength = 180.28 - 40 = 140.28$


$y′′ = y′$


После всех этих манипуляций дальнейшее решение задачи сводится к нахождению углов a и b треугольника:


Перед нахождением углов необходи��о найти третью сторону C этого треугольника. Это расстояние ни что иное как длина вектора и рассчитывается по формуле:

$C = \sqrt{x′′^2 + y′′^2} = \sqrt{140.28^2 + (-20)^2} = 141.70$


Теперь необходимо выполнить проверку, сможет ли конечность дотянуться до этой точки. Если С больше чем сумма длин FEMUR и TIBIA, то точка является не достижимой. В нашем случае 141.70 < 141 + 85 — точка достижима.

Теперь нам известны все стороны треугольника и можно найти нужные нам углы a и b используя теорему косинусов:

$a = acos ({ A^2 + C^2 - B^2 \over 2AC}) = 72.05°$


$b = acos ({ B^2 + A^2 - C^2 \over 2BA}) = 72.95°$


Полученные углы не применимы для скармливания их сервоприводам, так как тут не учитывается начальное положение и угол наклона прямой С к оси X. Если начальные углы FEMUR и TIBIA нам известны (135° и 45°), то угол наклона C к оси X нам не известен. Найти его можно используя функцию atan2(y′′, x′′):

$φ = atan2(y′′, x′′) = atan2(-20, 140.28) = -8.11°$


Наконец-то можно рассчитать угол поворота сервоприводов FEMUR и TIBIA:

$FEMUR = femurZeroRotate - a - φ = 135 - 72.05 + 8.11 = 71.06°$


$FEMUR = b - tibiaZeroRotate = 45 - 72.95 = 27.95°$



Давайте проверим наши расчеты:


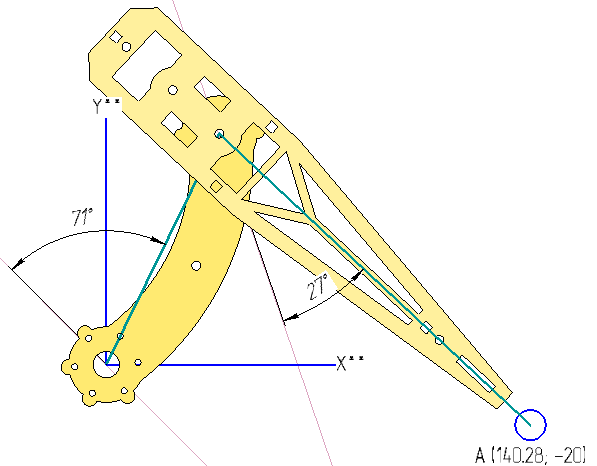
Вроде похоже на правду.

Итог


Рассчитанные углы COXA, FEMUR и TIBIA пригодны для скармливания их сервоприводам. Можно заметить, что угол COXA отрицательный и соответственно возникает вопрос: «А как повернуть привод на -11.3 градуса?». Хитрость состоит в том, что я использую нейтральное положение сервопривода COXA в качестве логического нуля, это позволяет вращать привод как на положительные углы, так и на отрицательные. Это конечно очевидно, но я думаю будет не лишним об этом упомянуть. Более подробно расскажу об этом в следующих статьях, когда буду рассказывать о реализации всего выше упомянутого.

Исходники


Хватит слов, дай гляну код 
#define RAD_TO_DEG(rad)                ((rad) * 180.0 / M_PI)
#define DEG_TO_RAD(deg)                ((deg) * M_PI / 180.0)

typedef enum {
    LINK_COXA,
    LINK_FEMUR,
    LINK_TIBIA
} link_id_t;

typedef struct {
    
    // Current link state
    float angle;
    
    // Link configuration
    uint32_t length;
    int32_t  zero_rotate;
    int32_t  min_angle;
    int32_t  max_angle;
    
} link_info_t;

typedef struct {
    
    point_3d_t position;
    path_3d_t  movement_path;
    
    link_info_t links[3];
    
} limb_info_t;

//  ***************************************************************************
/// @brief  Calculate angles
/// @param  info: limb info @ref limb_info_t
/// @return true - calculation success, false - no
//  ***************************************************************************
static bool kinematic_calculate_angles(limb_info_t* info) {

    int32_t coxa_zero_rotate_deg = info->links[LINK_COXA].zero_rotate;
    int32_t femur_zero_rotate_deg = info->links[LINK_FEMUR].zero_rotate;
    int32_t tibia_zero_rotate_deg = info->links[LINK_TIBIA].zero_rotate;
    uint32_t coxa_length = info->links[LINK_COXA].length;
    uint32_t femur_length = info->links[LINK_FEMUR].length;
    uint32_t tibia_length = info->links[LINK_TIBIA].length;
    
    float x = info->position.x;
    float y = info->position.y;
    float z = info->position.z;
    
    
    // Move to (X*, Y*, Z*) coordinate system - rotate
    float coxa_zero_rotate_rad = DEG_TO_RAD(coxa_zero_rotate_deg);
    float x1 = x * cos(coxa_zero_rotate_rad) + z * sin(coxa_zero_rotate_rad);
    float y1 = y;
    float z1 = -x * sin(coxa_zero_rotate_rad) + z * cos(coxa_zero_rotate_rad);


    //
    // Calculate COXA angle
    //
    float coxa_angle_rad = atan2(z1, x1);
    info->links[LINK_COXA].angle = RAD_TO_DEG(coxa_angle_rad);


    //
    // Prepare for calculation FEMUR and TIBIA angles
    //
    // Move to (X*, Y*) coordinate system (rotate on axis Y)
    x1 = x1 * cos(coxa_angle_rad) + z1 * sin(coxa_angle_rad);

    // Move to (X**, Y**) coordinate system (remove coxa from calculations)
    x1 = x1 - coxa_length;
    
    // Calculate angle between axis X and destination point
    float fi = atan2(y1, x1);

    // Calculate distance to destination point
    float d = sqrt(x1 * x1 + y1 * y1);
    if (d > femur_length + tibia_length) {
        return false; // Point not attainable
    }
    
    
    //
    // Calculate triangle angles
    //
    float a = tibia_length;
    float b = femur_length;
    float c = d;

    float alpha = acos( (b * b + c * c - a * a) / (2 * b * c) );
    float gamma = acos( (a * a + b * b - c * c) / (2 * a * b) );


    //
    // Calculate FEMUR and TIBIA angle
    //
    info->links[LINK_FEMUR].angle = femur_zero_rotate_deg - RAD_TO_DEG(alpha) - RAD_TO_DEG(fi);
    info->links[LINK_TIBIA].angle = RAD_TO_DEG(gamma) - tibia_zero_rotate_deg;
    
    //
    // Check angles
    //
    if (info->links[LINK_COXA].angle < info->links[LINK_COXA].min_angle || info->links[LINK_COXA].angle > info->links[LINK_COXA].max_angle) {
        return false;
    }
    if (info->links[LINK_FEMUR].angle < info->links[LINK_FEMUR].min_angle || info->links[LINK_FEMUR].angle > info->links[LINK_FEMUR].max_angle) {
        return false;
    }
    if (info->links[LINK_TIBIA].angle < info->links[LINK_TIBIA].min_angle || info->links[LINK_TIBIA].angle > info->links[LINK_TIBIA].max_angle) {
        return false;
    }

    return true;
}


Алгоритм в действии



Тут случайно получилась последовательность, чем-то напоминающая танец


P.S.


Буду рад если кто-нибудь сможет упростить этот алгоритм. Я делал его таким, чтобы понять его спустя, допустим, пол года.