Прелюдия
Численное решение линейных систем уравнений является незаменимым шагом во многих сферах прикладной математики, инженерии и IT-индустрии, будь то работа с графикой, расчёт аэродинамики какого-нибудь самолёта или оптимизация логистики. Модная нынче «машинка» без этого тоже не особо бы продвинулась. Причём решение линейных систем, как правило, сжирает наибольший процент из всех вычислительных затрат. Понятно, что эта критическая составляющая требует максимальной оптимизации по скорости.
Часто работают с т.н. разреженными матрицами — теми, у которых нулей на порядки больше остальных значений. Такое, например, неизбежно, если имеешь дело с уравнениями в частных производных или с какими-нибудь другими процессами, в которых возникающие элементы в определяющих линейных соотношениях связаны лишь с «соседями». Вот возможный пример разреженной матрицы для известного в классической физике одномерного уравнения Пуассона
Противоположные им матрицы — те, в которых на количество нулей не обращают внимания и учитывают все компоненты без исключения, — называют плотными.
Разреженные матрицы часто, из разнообразных соображений, представляют в сжато-столбцовом формате — Compressed Sparse Column (CSC). При таком описании используются два целочисленных массива и один с плавающей точкой. Пусть у матрицы всего
массивы будут
Методы решения линейных систем делятся на два больших класса — прямые и итерационные. Прямые основаны на возможности представить матрицу в виде произведения двух более простых матриц, чтобы затем расщепить решение на два простых этапа. Итерационные используют уникальные свойства линейных пространств и работают на древнем как мир способе последовательного приближения неизвестных к искомому решению, причём в самом процессе сходимости матрицы используются, как правило, только для умножения их на векторы. Итерационные методы гораздо дешевле прямых, но вяло работают на плохо обусловленных матрицах. Когда важна железобетонная надёжность — используют прямые. Вот их я тут и хочу немного затронуть.
Допустим, для квадратной матрицы
Как в этом случае решать систему уравнений
Центральная идея состоит в том, что, по нахождении
Второй этап — обратный ход (backward solve = backward substitution). Имея найденный вектор
и наше решение будет
Если матрица плотная, то есть полностью представлена в виде какого-то массива, одномерного или двумерного, и доступ к конкретному элементу в ней совершается за время
Алгоритм 1:
void forward_solve (const std::vector<size_t>& iA, const std::vector<size_t>& jA, const std::vector<double>& vA, std::vector<double>& x)
{
size_t j, p, n = x.size();
for (j = 0; j < n; j++) // цикл по столбцам
{
x[j] /= vA[jA[j]];
for (p = jA[j]+1; p < jA[j+1]; p++)
x[iA[p]] -= vA[p] * x[j] ;
}
}
Всё дальнейшее обсуждение будет касаться только прямого хода для решения нижнетреугольной системы
Завязка
А что если правая часть, т.е. вектор справа от знака равенства
Алгоритм 2:
void fake_sparse_forward_solve (const std::vector<size_t>& iA, const std::vector<size_t>& jA, const std::vector<double>& vA, std::vector<double>& x)
{
size_t j, p, n = x.size();
for (j = 0; j < n; j++) // цикл по столбцам
{
if(x[j])
{
x[j] /= vA[jA [j]];
for (p = jA[j]+1; p < jA[j+1]; p++)
x[iA[p]] -= vA[p] * x[j];
}
}
}
Единственное, что мы добавили — это оператор
if, целью которого является сокращение количества арифметических действий до их фактического числа. Если, например, вся правая часть состоит из нулей, то и считать ничего не надо: решение и будет правой частью. Всё выглядит здорово и конечно же будет работать, но тут, после долгой прелюдии, наконец-то видна проблема — асимптотически низкая производительность данного решателя в случае больших систем. А всё из-за самого факта наличия цикла
for. В чём же проблема? Даже если условие внутри if оказывается истинным крайне редко, от самого цикла никуда не деться, и это порождает сложность алгоритма Ну хорошо, допустим. Даже если так, почему нельзя просто стерпеть прогон
for в холостую, ведь реальных вычислений с вещественными числами, т.е. тех, что попадают под if, всё равно будет мало? А дело в том, что данная процедура прямого хода с разреженной правой частью сама часто используется во внешних циклах и лежит в основе разложения Холецкого Теорема. Если матрица симметричная положительно-определённая (SPD), то её можно представить в виде
Для сильно разреженных SPD матриц используют верхнестороннее (up-looking) разложение Холецкого. Схематически представляя разложение в матрично-блочном виде
весь процесс факторизации можно логически разбить всего на три шага.
Алгоритм 3:
- верхний метод разложения Холецкого меньшей размерности
(рекурсия!)
- нижнетреугольная система с разреженной правой частью
(вот оно!)
- вычисление
(тривиальная операция)
На практике это реализуется так, что в одном большом цикле совершаются шаги 3 и 2, причём именно в этом порядке. Таким образом, осуществляется прогон матрицы по диагонали сверху вниз, увеличивающий матрицу
Если в подобном аглоритме сложность прямого хода в шаге 2 будет
State of the art
Многие алгоритмы так или иначе основаны на мимикрировании человеческих действий при решении проблем. Если дать человеку нижнетреугольную линейную систему с правой частью, в которой только 1-2 ненуля, то он сначала, конечно, пробежит вектор правой части глазами сверху вниз ( тот проклятый цикл сложности
// если столбец с индексом j, то пробегаем только ненулевые элементы:
for (size_t p = jA[j]; p < jA[j+1]; p++)
// получаем ненулевой элемент vA[p] матрицы на пересечении строки iA[p] и столбца j
Сложность такого доступа —
В таком случае, мы можем уловить самую суть происходящего при решении методом прямого хода
Определим для нижнетреугольной матрицы, у которой отсутствуют нули на диагонали, граф связности. Будем считать, что нумерация строк и столбцов начинается с нуля.
Определение. Графом связности для нижнетреугольной матрицы
Вот, например, как выглядит граф связности для нижнетреугольной матрицы

в которой цифры просто соответствуют порядковому номеру диагонального элемента, а точки обозначают ненулевые компоненты ниже диагонали:
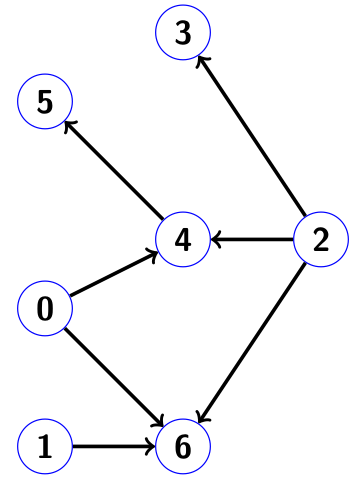
Определение. Достижимостью ориентированного графа
Пример: для графа с картинки
Если представить каждый узел графа как номер столбца породившей его матрицы, то соседние узлы, в которые направлены его рёбра, соответствуют номерам строк ненулевых компонент в этом столбце.
Пусть
Теорема Гильберта (нет, не того, чьим именем названы пространства) Множество
Добавочка от себя: в теореме мы не учитываем маловероятную возможноть того, что ненулевые числа в правой части, при уничтожении стобцов, могут сократиться в ноль, например, 3 — 3 = 0. Этот эффект называется numerical cancellation. Учитывать такие спонтанно возникающие нули бессмысленная трата времени, и они воспринимаются как и все остальные числа в ненулевых позициях.
Эффективный метод проведения прямого хода с заданной разреженной правой частью, в предположении, что мы имеем прямой доступ к ненулевым её компонентам по индексам, заключается в следующем.
- Пробегаем граф методом "поиск в глубину" (depth first search), последовательно стартуя от индекса
каждой ненулевой компоненты правой части. Запись найденных узлов в массив
при этом совершаем в том порядке, в котором мы возвращаемся по графу назад! По аналогии с армией захватчиков: оккупируем страну без жестокости, но когда нас стали гнать обратно, мы, разозлённые, уничтожаем всё на своём пути.
Стоит отметить, что абсолютно не обязательно, чтобы список индексовбыл отсортирован по возврастанию при подаче его на вход алгоритму «поиск в глубину». Стартовать можно в любом порядке на множестве
. Различный порядок следования принадлежащих множеству
индексов не влияет на итоговое решение, как мы увидим на примере.
Этот шаг не требует вообще никаких знаний о вещественночисленном массиве! Добро пожаловать в мир символьного анализа при работе с прямыми разреженными решателями!
- Переходим уже к самому решению, имея в собственном распоряжении массив
с предыдущего шага. Столбцы уничтожаем в порядке, обратном порядку записи этого массива. Вуаля!
Пример
Рассмотрим пример, на котором оба шага детально продемонстрированы. Пусть у нас есть матрица размера 12 x 12 следующего вида:

Соответствующий ей граф связности имеет вид:
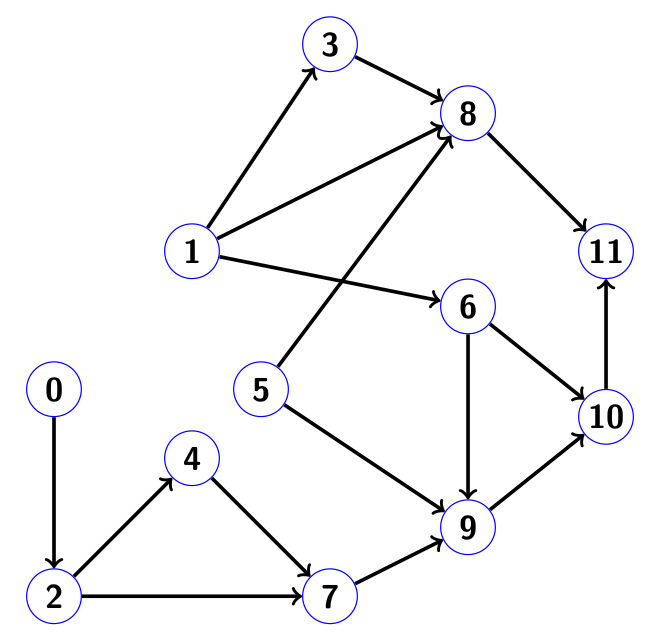
Пусть в правой части ненули находятся только на позициях 3 и 5, то есть

При возвращении назад, заносим индексы в наш массив индексов ненулевых компонент решения

Мутно-зелёные узлы 8 и 11 — те, которые мы хотели посетить во время второго пробега, но не смогли, т.к. уже посетили во время первого.
Таким образом, массив

Обратим внимание: в таком порядке уничтожения столбцов номер 3 встретится позже номеров 5, 9 и 10! Столбцы уничтожаются не в отсортированном по возрастанию порядке, что было бы ошибкой для плотных, т.е. неразреженных матриц. Но для разреженных матриц подобное в порядке вещей. Как видно из ненулевой структуры матрицы в данном примере, использование столбцов 5, 9 и 10 до столбца 3 не исказит в ответе компоненты
Если же мы будем делать обход графа сначала с индекса 5, а потом с индекса 3, то наш массив получится
Сложность всех наших операций масштабируется по количеству фактических арифметических операций и количеству ненулевых компонент в правой части, но никак не по размеру матрицы! Мы добились своего.
Критика
ОДНАКО! Критически настроенный читатель заметит, что само предположение в начале, будто у нас есть «прямой доступ к ненулевым компонентам правой части по индексам», уже означает, что когда-то ранее мы пробежали правую часть сверху вниз, чтобы найти эти самые индексы и организовать их в массиве
А ведь действительно, для разового решения разреженной нижнетреугольной системы с разреженной же правой частью, изначально заданной в виде плотного вектора, нет смысла тратить время разработчика на все упомянутые выше алгоритмы. Они могут оказаться даже медленнее метода в лоб, представленного алгоритмом 2 выше. Но, как уже было сказано ранее, этот аппарат незаменим при факторизациях Холецкого, поэтому помидорами в меня кидаться не стоит. Действительно, перед запуском алгоритма 3, вся необходимая память максимальной длины выделяется сразу и требует
Реализация на C++
Сам граф как структуру данных в коде строить не обязательно. Достаточно его использовать неявно при работе с матрицей напрямую. Вся требуемая связность будет учитываться алгоритмом. Поиск в глубину конечно же удобно реализовать с помощью банальной рекурсии. Вот, например, как выглядит рекурсивный поиск в глубину на базе одного стартового индекса:
/*
j - стартовый индекс
iA, jA - целочисленные массивы нижнетреугольной матрицы, представленной в формате CSC
top - значение текущей глубины массива nnz(x); в самом начале передаём 0
result - массив длины N, на выходе содержит nnz(x) с индекса 0 до top-1 включительно
marked - массив меток длины N; на вход подаём заполненным нулями
*/
void DepthFirstSearch(size_t j, const std::vector<size_t>& iA, const std::vector<size_t>& jA, size_t& top, std::vector<size_t>& result, std::vector<int>& marked)
{
size_t p;
marked[j] = 1; // помечаем узел j как посещённый
for (p = jA[j]; p < jA[j+1]; p++) // для каждого ненулевого элемента в столбце j
{
if (!marked[iA[p]]) // если iA[p] не помечен
{
DepthFirstSearch(iA[p], iA, jA, top, result, marked); // Поиск в глубину на индексе iA[p]
}
}
result[top++] = j; // записываем j в массив nnz(x)
}Если в самом первом вызове
DepthFirstSearch передать переменную top равную нулю, то после завершения всей рекурсивной процедуры переменная top будет равняться количеству найденных индексов в массиве result. Домашнее задание: напишите ещё одну функцию, которая принимает массив индексов ненулевых компонент в правой части и последовательно передаёт их функции DepthFirstSearch. Без этого алогоритм не полный. Обратите внимание: массив вещественных чисел Несмотря на простоту, дефект реализации очевиден: для больших систем переполнение стека не за горами. Ну тогда есть вариант, основанный на цикле вместо рекурсии. Он посложнее для понимания, но уже годен на все случаи жизни:
/*
j - стартовый индекс
N - размер матрицы
iA, jA - целочисленные массивы нижнетреугольной матрицы, представленной в формате CSC
top - значение текущей глубины массива nnz(x)
result - массив длины N, на выходе содержит часть nnz(x) с индексов top до ret-1 включительно, где ret - возвращаемое значение функции
marked - массив меток длины N
work_stack - вспомогательный рабочий массив длины N
*/
size_t DepthFirstSearch(size_t j, size_t N, const std::vector<size_t>& iA, const std::vector<size_t>& jA, size_t top, std::vector<size_t>& result, std::vector<int>& marked, std::vector<size_t>& work_stack)
{
size_t p, head = N - 1;
int done;
result[N - 1] = j; // инициализируем рекурсионный стек
while (head < N)
{
j = result[head]; // получаем j с верхушки рекурсионного стека
if (!marked[j])
{
marked[j] = 1; // помечаем узел j как посещённый
work_stack[head] = jA[j];
}
done = 1; // покончили с узлом j в случае отсутствия непосещённых соседей
for (p = work_stack[head] + 1; p < jA[j+1]; p++) // исследуем всех соседей j
{
// работаем с cоседом с номером iA[p]
if (marked[iA[p]]) continue; // узел iA[p] посетили раньше, поэтому пропускаем
work_stack[head] = p; // ставим на паузу поиск по узлу j
result[--head] = iA[p]; // запускаем поиск в глубину на узле iA[p]
done = 0; // с узлом j ещё не покончили
break;
}
if (done) // поиск в глубину на узле j закончен
{
head++; // удаляем j из рекурсионного стека
result[top++] = j; // помещаем j в выходной массив
}
}
return (top);
}А вот так уже выглядит сам генератор ненулевой структуры вектора решения
/*
iA, jA - целочисленные массивы матрицы, представленной в формате CSC
iF - массив индексов ненулевых компонент вектора правой части f
nnzf - количество ненулей в правой части f
result - массив длины N, на выходе содержит nnz(x) с индексов 0 до ret-1 включительно, где ret - возвращаемое значение функции
marked - массив меток длины N, передаём заполненным нулями
work_stack - вспомогательный рабочий массив длины N
*/
size_t NnzX(const std::vector<size_t>& iA, const std::vector<size_t>& jA, const std::vector<size_t>& iF, size_t nnzf, std::vector<size_t>& result, std::vector<int>& marked, std::vector<size_t>& work_stack)
{
size_t p, N, top;
N = jA.size() - 1;
top = 0;
for (p = 0; p < nnzf; p++)
if (!marked[iF[p]]) // начинаем поиск в глубину на непомеченном узле
top = DepthFirstSearch(iF[p], N, iA, jA, vA, top, result, marked, work_stack);
for (p = 0; p < top; p++)
marked[result[p]] = 0; // очищаем метки
return (top);
}Наконец, объединяя всё во едино, пишем сам нижнетреугольный решатель для случая разреженной правой части:
/*
iA, jA, vA - массивы матрицы, представленной в формате CSC
iF - массив индексов ненулевых компонент вектора правой части f
nnzf - количество ненулей в правой части f
vF - массив ненулевых компонент вектора правой части f
result - массив длины N, на выходе содержит nnz(x) с индексов 0 до ret-1 включительно, где ret - возвращаемое значение функции
marked - массив меток длины N, передаём заполненным нулями
work_stack - вспомогательный рабочий массив длины N
x - вектор решения длины N, которое получим на выходе; на входе заполнен нулями
*/
size_t lower_triangular_solve (const std::vector<size_t>& iA, const std::vector<size_t>& jA, const std::vector<double>& vA, const std::vector<size_t>& iF, size_t nnzf, const std::vector<double>& vF, std::vector<size_t>& result, std::vector<int>& marked, std::vector<size_t>& work_stack, std::vector<double>& x)
{
size_t top, p, j;
ptrdiff_t px;
top = NnzX(iA, jA, iF, nnzf, result, marked, work_stack);
for (p = 0; p < nnzf; p++) x[iF[p]] = vF[p]; // заполняем плотный вектор
for (px = top; px > -1; px--) // прогон в обратном порядке
{
j = result[px]; // x(j) будет ненулём
x [j] /= vA[jA[j]]; // мгновенное нахождение x(j)
for (p = jA[j]+1; p < jA[j+1]; p++)
{
x[iA[p]] -= vA[p]*x[j]; // уничтожение j-ого столбца
}
}
return (top) ;
}
Видим, что цикл наш пробегает только по индексам массива
Cуществует реализация, которая не использует массив меток
marked с целью экономии памяти. Вместо этого, используется дополнительное множество индексов В качестве заключения
Процесс решения разреженной системы линейных уравнений прямым методом, как правило, разбивается на три этапа:
- Символьный анализ
- Численная факторизация на основе данных сивольного анализа
- Решение полученных треугольных систем с плотной правой частью
Второй шаг — численная факторизация — наиболее ресурсозатратная часть и пожирает большую часть (>90%) расчётного времени. Цель первого шага — понизить дороговизну второго. Пример символьного анализа и был представлен в данном посте. Однако именно первый шаг требует самого длительного времени разработки и максимальных умственных затрат со стороны разработчика. Хороший символьный анализ требует знания теории графов и деревьев и владения «алгоритмическим чутьём». Второй шаг несоизмеримо проще в реализации.
Ну а третий шаг и по реализации, и по расчётному времени в большинстве случаев самый непритязательный.
Хорошее введение в прямые методы для разреженных систем есть в книге профессора факультета компьютерных наук университета Texas A&M Тима Девиса под названием "Direct Methods for Sparse Linear Systems". Там и описан показанный выше алгоритм. С самим Девисом я не знаком, хотя в своё время сам работал в том же университете (правда, на другом факультете). Если не ошибаюсь, Девис сам участвовал в разработке решателей, используемых в Матлабе(!). Более того, он причастен даже к генераторам картинок в Google Street View (метод наименьших квадратов). Кстати, на том же факультете числится никто иной как сам Бьёрн Страуструп — создатель языка C++.
Возможно, когда-нибудь напишу ещё что-нибудь на тему разреженных матриц или численных методов вообще. Всем добра!