SciPy, оптимизация / Habr

SciPy (произносится как сай пай) — это пакет прикладных математических процедур, основанный на расширении Numpy Python. С SciPy интерактивный сеанс Python превращается в такую же полноценную среду обработки данных и прототипирования сложных систем, как MATLAB, IDL, Octave, R-Lab и SciLab. Сегодня я хочу коротко рассказать о том, как следует применять некоторые известные алгоритмы оптимизации в пакете scipy.optimize. Более подробную и актуальную справку по применению функций всегда можно получить с помощью команды help() или с помощью Shift+Tab.

Введение

Дабы избавить самого себя и читателей от поиска и чтения первоисточников, ссылки на описания методов будут в основном на википедию. Как правило, этой информации достаточно для понимания методов в общих чертах и условий их применения. Для понимания сути математических методов идем по ссылкам на более авторитетные публикации, которые можно найти в конце каждой статьи или в любимой поисковой системе.

Итак, модуль scipy.optimize включает в себя реализацию следующих процедур:

Условной и безусловной минимизации скалярных функций нескольких переменных (minim) с помощью различных алгоритмов (симплекс Нелдера-Мида, BFGS, сопряженных градиентов Ньютона, COBYLA и SLSQP)
Глобальной оптимизации (например: basinhopping, diff_evolution)
Минимизация остатков МНК (least_squares) и алгоритмы подгонки кривых нелинейным МНК (curve_fit)
Минимизации скалярной функций одной переменной (minim_scalar) и поиска корней (root_scalar)
Многомерные решатели системы уравнений (root) с использованием различных алгоритмов (гибридный Пауэлла, Левенберг-Марквардт или крупномасштабные методы, такие как Ньютона-Крылова).

В этой статье мы рассмотрим только первый пункт из всего этого списка.

Безусловная минимизация скалярной функции нескольких переменных

Функция minim из пакета scipy.optimize предоставляет общий интерфейс для решения задач условной и безусловной минимизации скалярных функций нескольких переменных. Чтобы продемонстрировать ее работу, нам понадобится подходящая функция нескольких переменных, которую мы будем по-разному минимизировать.

Для этих целей прекрасно подойдет функция Розенброка от N переменных, которая имеет вид:

$f\left(\mathbf{x}\right)=\sum_{i=1}^{N-1}[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}]$

Несмотря на то, что функция Розенброка и ее матрицы Якоби и Гессе (первой и второй производной соответственно) уже определены в пакете scipy.optimize, определим ее самостоятельно.

import numpy as np

def rosen(x):
    """The Rosenbrock function"""
    return np.sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0, axis=0)

Для наглядности отрисуем в 3D значения функции Розенброка от двух переменных.

Код для отрисовки

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter

# Настраиваем 3D график
fig = plt.figure(figsize=[15, 10])
ax = fig.gca(projection='3d')

# Задаем угол обзора
ax.view_init(45, 30)

# Создаем данные для графика
X = np.arange(-2, 2, 0.1)
Y = np.arange(-1, 3, 0.1)
X, Y = np.meshgrid(X, Y)
Z = rosen(np.array([X,Y]))

# Рисуем поверхность
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm)
plt.show()

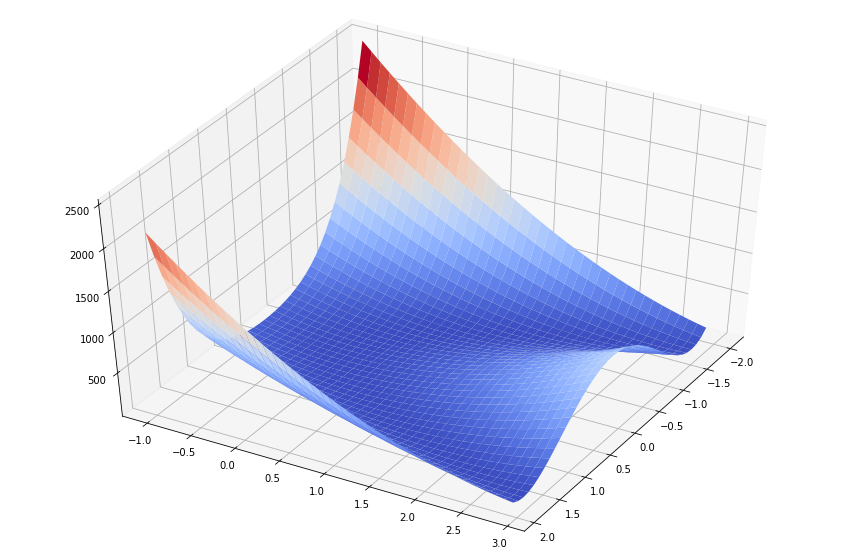
Зная заранее, что минимум равен 0 при $inline$ , рассмотрим примеры того, как определить минимальное значение функции Розенброка с помощью различных процедур scipy.optimize.

Симплекс-метод Нелдера-Мида (Nelder-Mead)

Пусть имеется начальная точка x0 в 5-мерном пространстве. Найдем ближайшую к ней точку минимума функции Розенброка с помощью алгоритма симплекса Nelder-Mead (алгоритм указан в качестве значения параметра method):

from scipy.optimize import minimize
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead',
    options={'xtol': 1e-8, 'disp': True})
print(res.x)

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 339
         Function evaluations: 571
[1. 1. 1. 1. 1.]

Симплекс-метод является самым простым способом свести к минимуму явно определенную и довольно гладкую функцию. Он не требует вычисления производных функции, достаточно задать только ее значения. Метод Нелдера-Мида является хорошим выбором для простых задач минимизации. Однако, поскольку он не использует оценки градиента, для поиска минимума может потребоваться больше времени.

Метод Пауэлла

Другим алгоритмом оптимизации, в котором вычисляются только значения ��ункций, является метод Пауэлла. Чтобы использовать его, нужно установить method = 'powell' в функции minim.

x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='powell',
    options={'xtol': 1e-8, 'disp': True})
print(res.x)

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19
         Function evaluations: 1622
[1. 1. 1. 1. 1.]

Алгоритм Бройдена-Флетчера-Голдфарба-Шанно (BFGS)

Для получения более быстрой сходимости к решению, процедура BFGS использует градиент целевой функции. Градиент может быть задан в виде функции или вычисляться с помощью разностей первого порядка. В любом случае, обычно метод BFGS требует меньше вызовов функций, чем симплекс-метод.

Найдем производную от функции Розенброка в аналитическом виде:

$\frac{\partial f }{\partial x_j} = \sum\limits_{i=1}^N 200(x_i - x_{i-1}^2)(\delta_{i,j} - 2x_{i-1, j}) - 2(1 - x_{i-1}) \delta_{i-1,j} =$

$= 200(x_j - x_{j-1}^2) - 400x_j(x_{j+1} - x_j^2) - 2(1-x_j)$

Это выражение справедливо для производных всех переменных, кроме первой и последней, которые определяются как:

$\frac{\partial f }{\partial x_0} = -400 x_0(x_1 - x_0^2) - 2(1 - x_0),$

$\frac{\partial f }{\partial x_{N-1}} = 200(x_{N-1} - x_{N-2}^2).$

Посмотрим на функцию Python, которая вычисляет этот градиент:

def rosen_der (x):
    xm = x [1: -1]
    xm_m1 = x [: - 2]
    xm_p1 = x [2:]
    der = np.zeros_like (x)
    der [1: -1] = 200 * (xm-xm_m1 ** 2) - 400 * (xm_p1 - xm ** 2) * xm - 2 * (1-xm)
    der [0] = -400 * x [0] * (x [1] -x [0] ** 2) - 2 * (1-x [0])
    der [-1] = 200 * (x [-1] -x [-2] ** 2)
    return der

Функция вычисления градиента указывается в качестве значения параметра jac функции minim, как показано ниже.

res = minimize(rosen, x0, method='BFGS', jac=rosen_der, options={'disp': True})
print(res.x)

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 25
         Function evaluations: 30
         Gradient evaluations: 30
[1.00000004 1.0000001  1.00000021 1.00000044 1.00000092]

Алгоритм сопряженных градиентов (Ньютона)

Алгоритм сопряженных градиентов Ньютона является модифицированным методом Ньютона.
Метод Ньютона основан на аппроксимации функции в локальной области полиномом второй степени:

$f\left(\mathbf{x}\right)\approx f\left(\mathbf{x}_{0}\right)+\nabla f\left(\mathbf{x}_{0}\right)\cdot\left(\mathbf{x}-\mathbf{x}_{0}\right)+\frac{1}{2}\left(\mathbf{x}-\mathbf{x}_{0}\right)^{T}\mathbf{H}\left(\mathbf{x}_{0}\right)\left(\mathbf{x}-\mathbf{x}_{0}\right)$

где $\mathbf{H}\left(\mathbf{x}_{0}\right)$ является матрицей вторых производных (матрица Гессе, гессиан).
Если гессиан положительно определен, то локальный минимум этой функции можно найти, приравняв нулевой градиент квадратичной формы к нулю. В результате получится выражение:

$\mathbf{x}_{\textrm{opt}}=\mathbf{x}_{0}-\mathbf{H}^{-1}\nabla f$

Обратный гессиан вычисляется с помощью метода сопряженных градиентов. Пример использования этого метода для минимизации функции Розенброка приведен ниже. Чтобы использовать метод Newton-CG, необходимо задать функцию, которая вычисляет гессиан.
Гессиан функции Розенброка в аналитическом виде равен:

$H_{i,j} = \frac{\partial^2 f }{\partial x_i x_j} = 200(\delta_{i,j} - 2x_{i-1} \delta{i-1,j} - 400x_i(\delta_{i+1,j} - 2x_i \delta{i,j}) - 400 \delta_{i,j} (x_{i+1} - x_i^2) + 2\delta_{i,j} =$

$= (202 + 1200x_i^2 - 400x_{i+1})\delta_{i,j} - 400x_i \delta_{i+1,j} - 400x_{i-1}\delta_{i-1,j}$

где $i, j \in \left[ 1, N-2 \right]$ и $i, j \in \left [0, N-1 \right]$ , определяют матрицу $N \times N$ .

Остальные ненулевые элементы матрицы равны:

$\frac{\partial^2 f }{\partial x_0^2} = 1200x_0^2 - 400x_1 +2$

$\frac{\partial^2 f }{\partial x_0 x_1} = \frac{\partial^2 f }{\partial x_1 x_0} = -400x_0$

$\frac{\partial^2 f }{\partial x_{N-1} x_{N-2}} = \frac{\partial^2 f }{\partial x_{N-2} x_{N-1}} = -400x_{N-2}$

$\frac{\partial^2 f }{\partial x_{N-1}^2} = 200x$

Например, в пятимерном пространстве N = 5, матрица Гессе для функции Розенброка имеет ленточный вид:

$\tiny \mathbf{H}=\begin{bmatrix} 1200x_{0}^{2}-400x_{1}+2 & -400x_{0} & 0 & 0 & 0\\ -400x_{0} & 202+1200x_{1}^{2}-400x_{2} & -400x_{1} & 0 & 0\\ 0 & -400x_{1} & 202+1200x_{2}^{2}-400x_{3} & -400x_{2} & 0\\ 0 & & -400x_{2} & 202+1200x_{3}^{2}-400x_{4} & -400x_{3}\\ 0 & 0 & 0 & -400x_{3} & 200\end{bmatrix}$

Код, который вычисляет этот гессиан вместе с кодом для минимизации функции Розенброка с помощью метода сопряженных градиентов (Ньютона):

def rosen_hess(x):
    x = np.asarray(x)
    H = np.diag(-400*x[:-1],1) - np.diag(400*x[:-1],-1)
    diagonal = np.zeros_like(x)
    diagonal[0] = 1200*x[0]**2-400*x[1]+2
    diagonal[-1] = 200
    diagonal[1:-1] = 202 + 1200*x[1:-1]**2 - 400*x[2:]
    H = H + np.diag(diagonal)
    return H

res = minimize(rosen, x0, method='Newton-CG', 
               jac=rosen_der, hess=rosen_hess,
               options={'xtol': 1e-8, 'disp': True})
print(res.x)

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 24
         Function evaluations: 33
         Gradient evaluations: 56
         Hessian evaluations: 24
[1.         1.         1.         0.99999999 0.99999999]

Пример с определением функции произведения гессиана и произвольного вектора

В реальных задачах вычисление и хранение всей матрицы Гессе может потребовать значительных ресурсов времени и памяти. При этом фактически нет н��обходимости задавать саму матрицу Гессе, т.к. для процедуры минимизации нужен только вектор, равный произведению гессиана с другим произвольным вектором. Таким образом, с вычислительной точки зрения намного предпочтительней сразу определить функцию, которая возвращает результат произведения гессиана с произвольным вектором.

Рассмотрим функцию hess, которая принимает вектор минимизации в качестве первого аргумента, а произвольный вектор — как второй аргумент (наряду с другими аргументами минимизируемой функции). В нашем случае вычислить произведение гессиана функции Розенброка с произвольным вектором не очень сложно. Если p — произвольный вектор, то произведение $H(x) \cdot p$ имеет вид:

$\mathbf{H}\left(\mathbf{x}\right)\mathbf{p}=\begin{bmatrix} \left(1200x_{0}^{2}-400x_{1}+2\right)p_{0}-400x_{0}p_{1}\\ \vdots\\ -400x_{i-1}p_{i-1}+\left(202+1200x_{i}^{2}-400x_{i+1}\right)p_{i}-400x_{i}p_{i+1}\\ \vdots\\ -400x_{N-2}p_{N-2}+200p_{N-1}\end{bmatrix}.$

Функция, вычисляющая произведение гессиана и произвольного вектора, передается как значение аргумента hessp функции minimize:

def rosen_hess_p(x, p):
    x = np.asarray(x)
    Hp = np.zeros_like(x)
    Hp[0] = (1200*x[0]**2 - 400*x[1] + 2)*p[0] - 400*x[0]*p[1]
    Hp[1:-1] = -400*x[:-2]*p[:-2]+(202+1200*x[1:-1]**2-400*x[2:])*p[1:-1] \
    -400*x[1:-1]*p[2:]
    Hp[-1] = -400*x[-2]*p[-2] + 200*p[-1]
    return Hp

res = minimize(rosen, x0, method='Newton-CG',
               jac=rosen_der, hessp=rosen_hess_p,
               options={'xtol': 1e-8, 'disp': True})

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 24
         Function evaluations: 33
         Gradient evaluations: 56
         Hessian evaluations: 66

Алгоритм доверительной области (trust region) сопряженных градиентов (Ньютона)

Плохая обусловленность матрицы Гессе и неверные направления поиска могут привести к тому, что алгоритм сопряженных градиентов Ньютона может быть неэффективным. В таких случаях предпочтение отдается методу доверительной области (trust-region) сопряженных градиентов Ньютона.

Пример с определением матрицы Гессе:

res = minimize(rosen, x0, method='trust-ncg',
               jac=rosen_der, hess=rosen_hess,
               options={'gtol': 1e-8, 'disp': True})
print(res.x)

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20
         Function evaluations: 21
         Gradient evaluations: 20
         Hessian evaluations: 19
[1. 1. 1. 1. 1.]

Пример с функцией произведения гессиана и произвольного вектора:

res = minimize(rosen, x0, method='trust-ncg', 
                jac=rosen_der, hessp=rosen_hess_p, 
                options={'gtol': 1e-8, 'disp': True})
print(res.x)

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20
         Function evaluations: 21
         Gradient evaluations: 20
         Hessian evaluations: 0
[1. 1. 1. 1. 1.]

Методы Крыловского типа

Подобно методу trust-ncg, методы Крыловского типа хорошо подходят для решения крупномасштабных задач, поскольку в них используется только матрично-векторные произведения. Их суть в решении задачи в доверительной области, ограниченной усеченным подпространством Крылова. Для неопределенных задач лучше использовать этот метод, так как он использует меньшее количество нелинейных итераций за счет меньшего количества матрично-векторных произведений на одну подзадачу, по сравнению с методом trust-ncg. Кроме того, решение квадратичной подзадачи находится более точно, чем методом trust-ncg.
Пример с определением матрицы Гессе:

res = minimize(rosen, x0, method='trust-krylov',
               jac=rosen_der, hess=rosen_hess,
               options={'gtol': 1e-8, 'disp': True})

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19
         Function evaluations: 20
         Gradient evaluations: 20
         Hessian evaluations: 18

print(res.x)

    [1. 1. 1. 1. 1.]

Пример с функцией произведения гессиана и произвольного вектора:

res = minimize(rosen, x0, method='trust-krylov',
               jac=rosen_der, hessp=rosen_hess_p,
               options={'gtol': 1e-8, 'disp': True})

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19
         Function evaluations: 20
         Gradient evaluations: 20
         Hessian evaluations: 0

print(res.x)

    [1. 1. 1. 1. 1.]

Алгоритм приближенного решения в доверительной области

Все методы (Newton-CG, trust-ncg и trust-krylov) хорошо подходят для решения крупномасштабных задач (с тысячами переменных). Это связано с тем, что лежащий в их основе алгоритм сопряженных градиентов подразумевает приближенное нахождение обратной матрицы Гессе. Решение находится итеративно, без явного разложения гессиана. Поскольку требуется определить только функцию для произведение гессиана и произвольного вектора, этот алгоритм особенно хорош для работы с разреженными (ленточными диагональными) матрицами. Это обеспечивает низкие затраты памяти и значительную экономию времени.

В задачах среднего размера затраты на хранение и факторизацию гессиана не имеют решающего значения. Это значит, чт�� можно получить решение за меньшее количество итераций, разрешив подзадачи области доверия почти точно. Для этого некоторые нелинейные уравнения решаются итеративно для каждой квадратичной подзадачи. Такое решение требует обычно 3 или 4 разложения Холецкого матрицы Гессе. В результате метод сходится за меньшее количество итераций и требует меньше вычислений целевой функции, чем другие реализованные методы доверительной области. Этот алгоритм подразумевает только определение полной матрицы Гессе и не поддерживает возможность использовать функцию произведения гессиана и произвольного вектора.

Пример с минимизацией функции Розенброка:

res = minimize(rosen, x0, method='trust-exact',
               jac=rosen_der, hess=rosen_hess,
               options={'gtol': 1e-8, 'disp': True})
res.x

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 13
         Function evaluations: 14
         Gradient evaluations: 13
         Hessian evaluations: 14

array([1., 1., 1., 1., 1.])

На этом, пожалуй, остановимся. В следующей статье постараюсь рассказать самое интересное об условной минимизации, приложении минимизации в решении задач аппроксимации, минимизации функции одной переменной, произвольных минимизаторах и поиске корней системы уравнений с помощью пакета scipy.optimize.

Источник: https://docs.scipy.org/doc/scipy/reference/