Доброго времени суток.
Последние несколько лет я посвятил исследованию и созданию различных алгоритмов пространственной обработки сигналов в адаптивных антенных решётках, и продолжаю заниматься этим в рамках своей работы в настоящее время. Здесь я хотел бы поделиться теми знаниями и фишками, которые открыл для себя. Надеюсь, что это будет полезно для людей начинающих изучать эту область обработки сигналов или же просто интересующихся.
Антенная решётка – это набор антенных элементов, некоторым образом размещённых в пространстве. Упрощённо структуру адаптивной антенной решётки, которую мы будем рассматривать, можно представить в следующем виде:
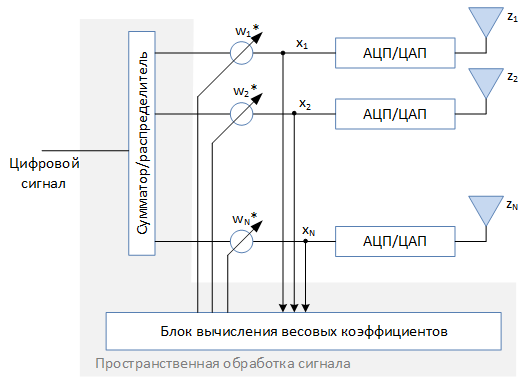
Адаптивные антенные решётки не редко называют «умными» антеннами (Smart antenna). «Умной» антенную решётку делает блок пространственной обработки сигнала и алгоритмы, реализованные в нём. Эти алгоритмы анализируют принимаемый сигнал и формируют набор весовых коэффициентов , которые определяют амплитуду и начальную фазу сигнала для каждого из элементов. Заданное амплитудно-фазовое распределение определяет диаграмму направленности всей решётки в целом. Возможность синтезировать диаграмму направленности необходимой формы и изменять её в процессе обработки сигнала — одна из главных особенностей адаптивных антенных решёток, позволяющая решать широкий спектр задач. Но обо всём по порядку.
, которые определяют амплитуду и начальную фазу сигнала для каждого из элементов. Заданное амплитудно-фазовое распределение определяет диаграмму направленности всей решётки в целом. Возможность синтезировать диаграмму направленности необходимой формы и изменять её в процессе обработки сигнала — одна из главных особенностей адаптивных антенных решёток, позволяющая решать широкий спектр задач. Но обо всём по порядку.
Диаграмма направленности характеризует мощность сигнала, излучаемую в некотором направлении. Для простоты положим элементы решётки изотропными, т.е. для каждого из них мощность излучаемого сигнала не зависит от направления. Усиление или ослабление мощности, излучаемой решёткой в некотором направлении, получается вследствие интерференции ЭМВ, излученных различными элементами антенной решётки. Устойчивая интерференционная картина для ЭМВ возможна только при условии их когерентности, т.е. разность фаз сигналов не должна меняться со временем. В идеальном случае каждый из элементов антенной решётки должен излучать гармонический сигнал на одной и той же несущей частоте . Однако на практике приходится работать с узкополосными сигналами, имеющими спектр конечной ширины
. Однако на практике приходится работать с узкополосными сигналами, имеющими спектр конечной ширины  .
.
Пусть все элементы АР излучают один и тот же сигнал с комплексной амплитудой . Тогда на удаленном приёмнике принятый от n-ного элемента сигнал можно представить в аналитическом виде:
. Тогда на удаленном приёмнике принятый от n-ного элемента сигнал можно представить в аналитическом виде: – задержка в распространении сигнала от антенного элемента до точки приёма.
– задержка в распространении сигнала от антенного элемента до точки приёма.
Такой сигнал является «квазигармоническим», и для выполнения условия когерентности необходимо, чтобы максимальная задержка в распространении ЭМВ между любыми двумя элементами была много меньше характерного времени изменения огибающей сигнала , т.е.
, т.е.  . Таким образом, условие на когерентность узкополосного сигнала можно записать следующим образом:
. Таким образом, условие на когерентность узкополосного сигнала можно записать следующим образом:
 — максимальное расстояние между элементами АР, а
— максимальное расстояние между элементами АР, а  — скорость света.
— скорость света.
При приёме сигнала когерентное суммирование производится в цифровом виде в блоке пространственной обработки. В этом случае комплексное значение цифрового сигнала на выходе этого блока определяется выражением: — операция эрмитового сопряжения.
— операция эрмитового сопряжения.
Векторное представление сигналов является одним из базовых при работе с антенными решётками, т.к. часто позволяет избежать громоздких математических выкладок. Кроме того, отождествление принятого в некоторый момент времени сигнала с вектором часто позволяет абстрагироваться от реальной физической системы и понять, что же именно происходит с точки зрения геометрии.
Чтобы рассчитать диаграмму направленности антенной решётки необходимо мысленно и последовательно «запустить» на неё набор плоских волн со всех возможных направлений. В этом случае значения элементов вектора x можно представить в следующем виде: и
и  – азимутальный угол и угол места, характеризующие направление прихода плоской волны,
– азимутальный угол и угол места, характеризующие направление прихода плоской волны,  – координата антенного элемента,
– координата антенного элемента,  – элемент фазирующего вектора s плоской волны с волновым вектором k (в англоязычной литературе фазирующий вектор называют steerage vector). Зависимость квадрата амплитуды величины y от
– элемент фазирующего вектора s плоской волны с волновым вектором k (в англоязычной литературе фазирующий вектор называют steerage vector). Зависимость квадрата амплитуды величины y от  и
и  определяет диаграмму направленности антенной решётки на приём при заданном векторе весовых коэффициентов w.
определяет диаграмму направленности антенной решётки на приём при заданном векторе весовых коэффициентов w.
Исследовать общие свойства диаграммы направленности антенных решёток удобно на линейной эквидистантной антенной решётке в горизонтально плоскости (т.е. ДН зависит только от азимутального угла ). Удобно с двух точек зрения: аналитических выкладок и визуального представления.
). Удобно с двух точек зрения: аналитических выкладок и визуального представления.
Рассчитаем ДН для единичного весового вектора ( ), следуя описанному выше подходу.
), следуя описанному выше подходу.
В итоге получим:
Полученная диаграмма направленности антенной решётки – периодическая функция от синуса угла. Это значит, что при определённых значениях соотношения d/λ она имеет дифракционные (дополнительные) максимумы.
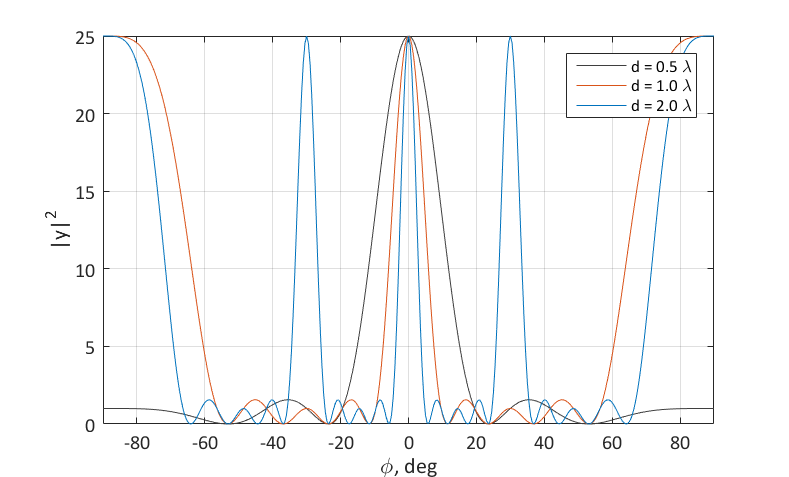 Ненормированная диаграмма направленности антенной решётки для N = 5
Ненормированная диаграмма направленности антенной решётки для N = 5
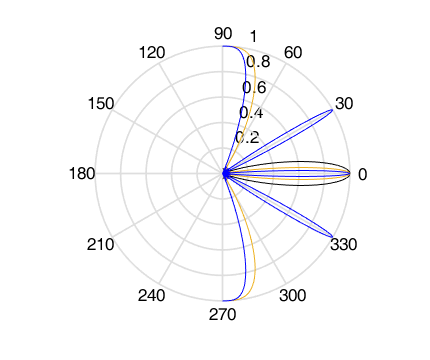 Нормированная диаграмма направленности антенной решётки для N = 5 в полярной системе координат
Нормированная диаграмма направленности антенной решётки для N = 5 в полярной системе координат
Положение «дифракционников» можно посмотреть напрямую из формулы для ДН. Однако мы попробуем понять, откуда они берутся физически и геометрически (в N-мерном пространстве).
Элементы фазирующего вектора s представляют собой комплексные экспоненты , значения которых определяются величиной обобщённого угла
, значения которых определяются величиной обобщённого угла  . Если существуют два обобщённых угла, соответствующих различным направлениям прихода плоской волны, для которых выполняется
. Если существуют два обобщённых угла, соответствующих различным направлениям прихода плоской волны, для которых выполняется  , то это значит две вещи:
, то это значит две вещи:
Связанные подобным образом направления прихода волны являются с точки зрения антенной решётки эквивалентными и не различимы между собой.
Как определить область углов, в которой всегда лежит только один главный максимум ДН? Сделаем это в окрестностях нулевого азимута из следующих соображений: величина набега фаз между двумя соседними элементами должна лежать в интервале от до
до  .
.
Видно, что размер области однозначности по углу зависит от соотношения d/λ. Если d = 0.5λ, то каждое направление прихода сигнала «индивидуально», а область однозначности охватывает полный диапазон углов. Если же d = 2.0λ, то направления 0, ±30, ±90 – эквивалентны. На диаграмме направленности появляются дифракционные лепестки.
Обычно, дифракционные лепестки стремятся подавить с помощью направленных антенных элементов. В этом случае полная диаграмма направленности антенной решётки является произведением ДН одного элемента и решётки изотропных элементов. Параметры ДН одного элемента обычно выбирают исходя из условия на область однозначности антенной решётки.
Широко известна инженерная формула для оценки ширины главного лепестка антенной системы: , где D – характерный размер антенны. Формула используется для различного вида антенн, в том числе зеркальных. Покажем, что она справедлива и для антенных решёток.
, где D – характерный размер антенны. Формула используется для различного вида антенн, в том числе зеркальных. Покажем, что она справедлива и для антенных решёток.
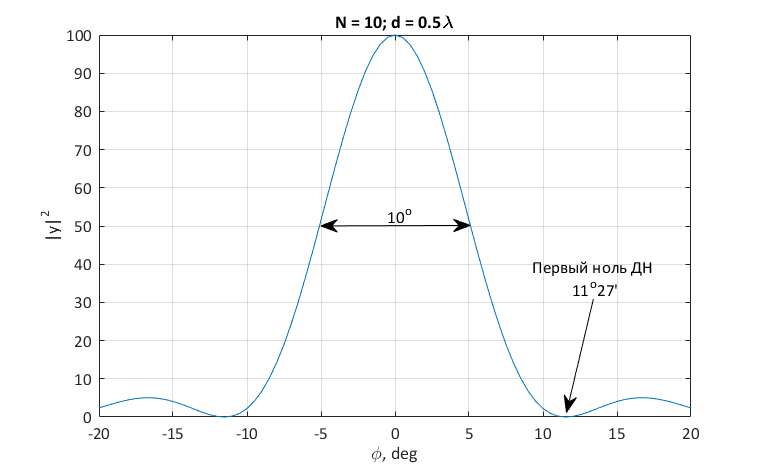
Определим ширину главного лепестка первыми нулями ДН в окрестности главного максимума. Числитель выражения для обращается в ноль при
обращается в ноль при  . Первые нули соответствуют m = ±1. Полагая
. Первые нули соответствуют m = ±1. Полагая  получаем
получаем  .
.
Обычно ширину ДН направленности АР определяют по уровню половинной мощности (-3 дБ). В этом случае используют выражение:
Шириной главного лепестка можно управлять, задавая различные значения амплитуд для весовых коэффициентов антенной решётки. Рассмотрим три распределения:
На рисунке показаны получившиеся нормированные диаграммы направленности в логарифмическом масштабе: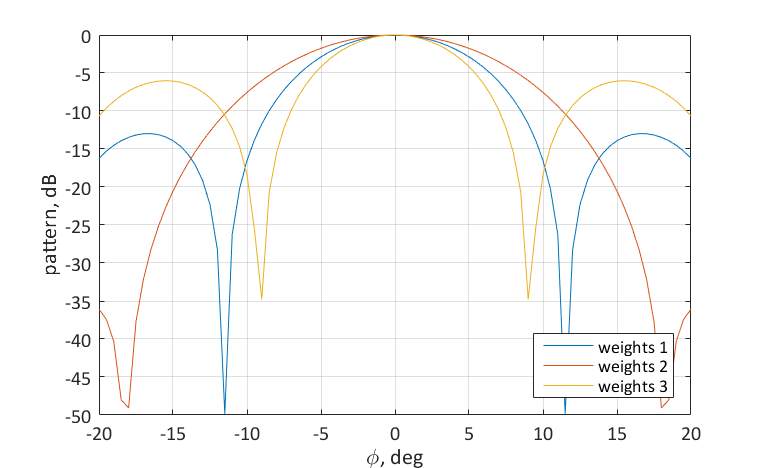
Из рисунка можно проследить следующие тенденции: спадающее к краям решётки распределение амплитуд весовых коэффициентов приводит к уширению главного лепестка ДН, но уменьшению уровня боковых лепестков. Увеличивающиеся к краям антенной решётки значения амплитуд, напротив, приводят к сужению главного лепестка и увеличению уровня боковиков. Здесь удобно рассмотреть предельные случаи:
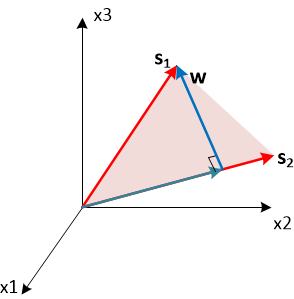
Итак, мы посмотрели, как можно регулировать ширину главного лепестка ДН АР. Теперь посмотрим, как порулить направлением. Вспомним векторное выражение для принятного сигнала. Пусть мы хотим, что бы максимум диаграммы направленности смотрел в некотором направлении . Это значит, что с этого направления должна приниматься максимальная мощность. Данному направлению соответствует фазирующий вектор
. Это значит, что с этого направления должна приниматься максимальная мощность. Данному направлению соответствует фазирующий вектор  в N-мерном векторном пространстве, а принимаемая мощность определяется как квадрат скалярного произведения этого фазирующего вектора на вектор весовых коэффициентов w. Скалярное произведение двух векторов максимально, когда они коллинеарны, т.е.
в N-мерном векторном пространстве, а принимаемая мощность определяется как квадрат скалярного произведения этого фазирующего вектора на вектор весовых коэффициентов w. Скалярное произведение двух векторов максимально, когда они коллинеарны, т.е.  , где β – некоторый нормирующий множит��ль. Таким образом, если мы выберем весовой вектор равным фазирующему для требуемого направления, то повернём максимум диаграммы направленности.
, где β – некоторый нормирующий множит��ль. Таким образом, если мы выберем весовой вектор равным фазирующему для требуемого направления, то повернём максимум диаграммы направленности.
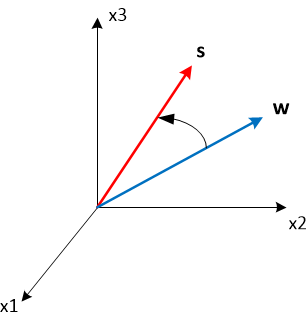
Рассмотрим в качестве примера следующие весовые коэффициенты:
Поставим задачку сформировать два главных максимума диаграммы направленности в направлении: -5° и 10°. Для этого выберем в качестве весового вектора взвешенную сумму фазирующих векторов для соответствующих направлений.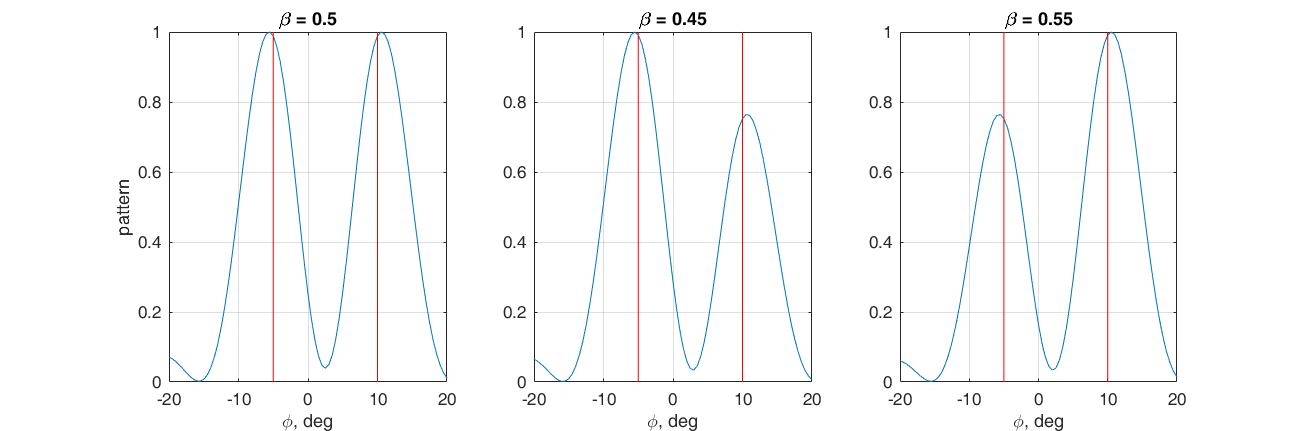 Регулируя коэффициент β можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если β больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
Регулируя коэффициент β можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если β больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
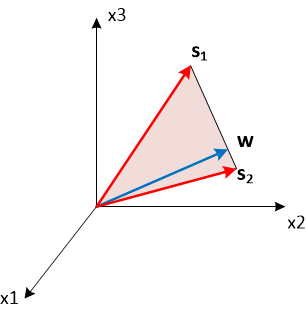
Однако стоит учесть, что оба главных лепестка имеют конечную ширину, и если мы захотим настроиться на два близких направления, то эти лепестки сольются в один, ориентированный на некоторое среднее направление.
Теперь попробуем настроить максимум диаграммы направленности на направление и одновременно подавить сигнал, приходящей с направления
и одновременно подавить сигнал, приходящей с направления  . Для этого необходимо выставить ноль ДН для соответствующего угла. Сделать это можно следующим образом:
. Для этого необходимо выставить ноль ДН для соответствующего угла. Сделать это можно следующим образом:
где , а
, а  .
.
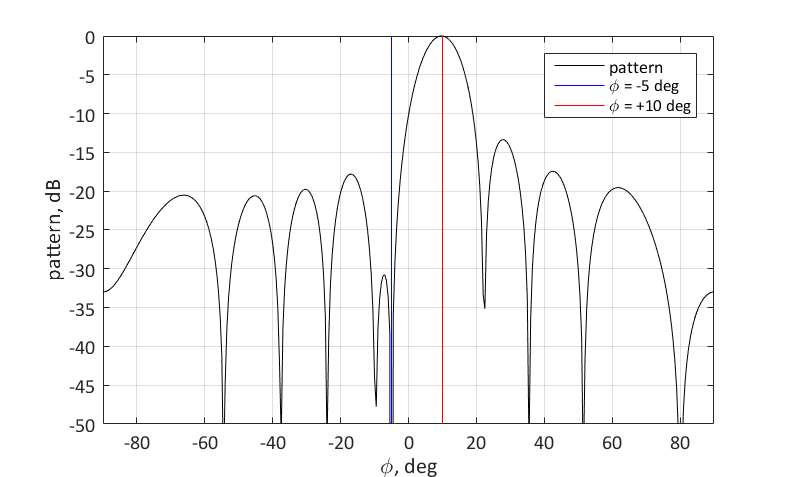
Геометрический смысл выбора весового вектора следующий. Мы хотим, что бы этот вектор w имел максимальную проекцию на и при этом был ортогонален вектору
и при этом был ортогонален вектору  . Вектор
. Вектор  можно представить в виде двух слагаемых: вектора коллинеарного
можно представить в виде двух слагаемых: вектора коллинеарного  и вектор ортогонального
и вектор ортогонального  . Чтобы удовлетворить постановке задачи, необходимо выбрать вторую компоненту в качестве вектора весовых коэффициентов w. Рассчитать коллинеарную компоненту можно спроектировав вектор
. Чтобы удовлетворить постановке задачи, необходимо выбрать вторую компоненту в качестве вектора весовых коэффициентов w. Рассчитать коллинеарную компоненту можно спроектировав вектор  на нормированный вектор
на нормированный вектор  с помощью скалярного произведения.
с помощью скалярного произведения. его коллинеарную компоненту, получим искомый весовой вектор.
его коллинеарную компоненту, получим искомый весовой вектор.
Спасибо за внимание
Последние несколько лет я посвятил исследованию и созданию различных алгоритмов пространственной обработки сигналов в адаптивных антенных решётках, и продолжаю заниматься этим в рамках своей работы в настоящее время. Здесь я хотел бы поделиться теми знаниями и фишками, которые открыл для себя. Надеюсь, что это будет полезно для людей начинающих изучать эту область обработки сигналов или же просто интересующихся.
Что такое адаптивная антенная решётка?
Антенная решётка – это набор антенных элементов, некоторым образом размещённых в пространстве. Упрощённо структуру адаптивной антенной решётки, которую мы будем рассматривать, можно представить в следующем виде:

Адаптивные антенные решётки не редко называют «умными» антеннами (Smart antenna). «Умной» антенную решётку делает блок пространственной обработки сигнала и алгоритмы, реализованные в нём. Эти алгоритмы анализируют принимаемый сигнал и формируют набор весовых коэффициентов
Как формируется диаграмма направленности?
Диаграмма направленности характеризует мощность сигнала, излучаемую в некотором направлении. Для простоты положим элементы решётки изотропными, т.е. для каждого из них мощность излучаемого сигнала не зависит от направления. Усиление или ослабление мощности, излучаемой решёткой в некотором направлении, получается вследствие интерференции ЭМВ, излученных различными элементами антенной решётки. Устойчивая интерференционная картина для ЭМВ возможна только при условии их когерентности, т.е. разность фаз сигналов не должна меняться со временем. В идеальном случае каждый из элементов антенной решётки должен излучать гармонический сигнал на одной и той же несущей частоте
Пусть все элементы АР излучают один и тот же сигнал с комплексной амплитудой
Такой сигнал является «квазигармоническим», и для выполнения условия когерентности необходимо, чтобы максимальная задержка в распространении ЭМВ между любыми двумя элементами была много меньше характерного времени изменения огибающей сигнала
При приёме сигнала когерентное суммирование производится в цифровом виде в блоке пространственной обработки. В этом случае комплексное значение цифрового сигнала на выходе этого блока определяется выражением:
Векторное представление сигналов является одним из базовых при работе с антенными решётками, т.к. часто позволяет избежать громоздких математических выкладок. Кроме того, отождествление принятого в некоторый момент времени сигнала с вектором часто позволяет абстрагироваться от реальной физической системы и понять, что же именно происходит с точки зрения геометрии.
Чтобы рассчитать диаграмму направленности антенной решётки необходимо мысленно и последовательно «запустить» на неё набор плоских волн со всех возможных направлений. В этом случае значения элементов вектора x можно представить в следующем виде:
Особенности диаграммы направленности антенной решётки
Исследовать общие свойства диаграммы направленности антенных решёток удобно на линейной эквидистантной антенной решётке в горизонтально плоскости (т.е. ДН зависит только от азимутального угла
Рассчитаем ДН для единичного весового вектора (
Математика тут
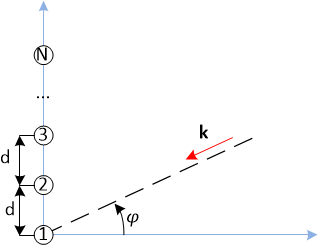
Проекция волнового вектора на вертикальную ось:
Вертикальная координата антенного элемента с индексом n:
Здесь d – период антенной решётки (расстояние между соседними элементами), λ — длина волны. Все иные элементы вектора r равны нулю.
Принимаемый антенной решёткой сигнал записывается в следующем виде:

Проекция волнового вектора на вертикальную ось:
Вертикальная координата антенного элемента с индексом n:
Здесь d – период антенной решётки (расстояние между соседними элементами), λ — длина волны. Все иные элементы вектора r равны нулю.
Принимаемый антенной решёткой сигнал записывается в следующем виде:
В итоге получим:
Периодичность диаграммы направленности
Полученная диаграмма направленности антенной решётки – периодическая функция от синуса угла. Это значит, что при определённых значениях соотношения d/λ она имеет дифракционные (дополнительные) максимумы.


Положение «дифракционников» можно посмотреть напрямую из формулы для ДН. Однако мы попробуем понять, откуда они берутся физически и геометрически (в N-мерном пространстве).
Элементы фазирующего вектора s представляют собой комплексные экспоненты
- Физически: плоские волновые фронты, приходящие с этих направлений, индуцируют на элементах антенной решётки идентичные амплитудно-фазовые распределения электромагнитных колебаний.
- Геометрически: фазирующие вектора для этих двух направлений совпадают.
Связанные подобным образом направления прихода волны являются с точки зрения антенной решётки эквивалентными и не различимы между собой.
Как определить область углов, в которой всегда лежит только один главный максимум ДН? Сделаем это в окрестностях нулевого азимута из следующих соображений: величина набега фаз между двумя соседними элементами должна лежать в интервале от
Видно, что размер области однозначности по углу зависит от соотношения d/λ. Если d = 0.5λ, то каждое направление прихода сигнала «индивидуально», а область однозначности охватывает полный диапазон углов. Если же d = 2.0λ, то направления 0, ±30, ±90 – эквивалентны. На диаграмме направленности появляются дифракционные лепестки.
Обычно, дифракционные лепестки стремятся подавить с помощью направленных антенных элементов. В этом случае полная диаграмма направленности антенной решётки является произведением ДН одного элемента и решётки изотропных элементов. Параметры ДН одного элемента обычно выбирают исходя из условия на область однозначности антенной решётки.
Ширина главного лепестка
Широко известна инженерная формула для оценки ширины главного лепестка антенной системы:
Определим ширину главного лепестка первыми нулями ДН в окрестности главного максимума. Числитель выражения для
Обычно ширину ДН направленности АР определяют по уровню половинной мощности (-3 дБ). В этом случае используют выражение:
Пример

Шириной главного лепестка можно управлять, задавая различные значения амплитуд для весовых коэффициентов антенной решётки. Рассмотрим три распределения:
- Равномерное распределение амплитуды (weights 1):
.
- Спадающее к краям решётки значения амплитуды (weights 2):
- Увеличивающиеся к краям решётки значения амплитуды(weights 3):
На рисунке показаны получившиеся нормированные диаграммы направленности в логарифмическом масштабе:

Из рисунка можно проследить следующие тенденции: спадающее к краям решётки распределение амплитуд весовых коэффициентов приводит к уширению главного лепестка ДН, но уменьшению уровня боковых лепестков. Увеличивающиеся к краям антенной решётки значения амплитуд, напротив, приводят к сужению главного лепестка и увеличению уровня боковиков. Здесь удобно рассмотреть предельные случаи:
- Амплитуды весовых коэффициентов всех элементов, кроме крайних, равны нулю. Веса для крайних элементов равны единице. В этом случае решётка становится эквивалентна двухэлементной АР с периодом D = (N-1)d. Не трудно прикинуть по представленной выше формуле ширину главного лепестка. При этом боковики превратятся в дифракционные максимумы и выровнятся по уровню с главным максимумом.
- Вес центрального элемента равен единице, а всех остальных – нулю. В этом случае мы получили по сути одну антенну с изотропной диаграммой направленности.
Направление главного максимума
Итак, мы посмотрели, как можно регулировать ширину главного лепестка ДН АР. Теперь посмотрим, как порулить направлением. Вспомним векторное выражение для принятного сигнала. Пусть мы хотим, что бы максимум диаграммы направленности смотрел в некотором направлении

Рассмотрим в качестве примера следующие весовые коэффициенты:
Поиграем с диаграммой направленности
Несколько максимумов
Поставим задачку сформировать два главных максимума диаграммы направленности в направлении: -5° и 10°. Для этого выберем в качестве весового вектора взвешенную сумму фазирующих векторов для соответствующих направлений.
 Регулируя коэффициент β можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если β больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
Регулируя коэффициент β можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если β больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
Однако стоит учесть, что оба главных лепестка имеют конечную ширину, и если мы захотим настроиться на два близких направления, то эти лепестки сольются в один, ориентированный на некоторое среднее направление.
Один максимум и ноль
Теперь попробуем настроить максимум диаграммы направленности на направление
где

Геометрический смысл выбора весового вектора следующий. Мы хотим, что бы этот вектор w имел максимальную проекцию на

Некоторые дополнительные замечания
- Везде выше я опустил вопрос нормировки весового вектора, т.е. его длины. Так вот, нормировка весового вектора не влияет на характеристики диаграммы направленности антенной решётки: направление главного максима, ширину главного лепестка и т.п. Можно также показать, что эта нормировка не влияет и на ОСШ на выходе блока пространственной обработки. В связи с этим при рассмотре��ии алгоритмов пространственной обработки сигнала обычно принимаю единичную нормировку весового вектора, т.е.
- Возможности по формированию ДН антенной решётки определяются количеством элементов N. Чем больше элементов, тем шире возможности. Тем больше степеней свободы при осуществлении пространственной весовой обработки, больше вариантов как «покрутить» весовым вектором в N-мерном пространстве.
- При осуществлении приёма ДН антенной решётки физически не существует, а все это существует лишь в «воображении» вычислительного блока, осуществляющего обработку сигнала. Это значит, что в один и тот же момент времени можно синтезировать несколько ДН и вести независимо обработку сигналов приходящих с различных направлений. В случае с передачей все несколько сложнее, однако также существует возможность синтезировать несколько ДН для передачи различных потоков данных. Такая технология в системах связи получила название MIMO.
- С помощью представленного matlab кода можно самостоятельно поиграться с ДН
Код% antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]);
Какие задачи можно решать с помощью адаптивной антенной решётки?
Оптимальный приём неизвестного сигнала
Если направление приход сигнала неизвестно (а если канал связи многолучевой, направлений вообще несколько), то проанализировав принимаемый антенной решёткой сигнал, можно сформировать оптимальный весовой вектор w так, что ОСШ на выходе блока пространственной обработки будет максимальным.
Оптимальный приём сигнала на фоне помех
Здесь задача ставится следующим образом: пространственные параметры ожидаемого полезного сигнала известны, однако во внешней среде существуют источники помех. Необходимо максимизировать ОСШП на выходе АР, максимально понизив влияние помех на приём сигнала.
Оптимальная переда сигнала пользователю
Данная задача решается в системах мобильной связи (4G, 5G), а также в Wi-Fi. Смысл прост: c помощью специальных пилотных сигналов в канале обратной связи пользователя производится оценка пространственных характеристик канала связи, и на её основе выбирается оптимальный для передачи вектор весовых коэффициентов.
Пространственное мультиплексирование потоков данных
Адаптивные антенные решётки позволяют вести передачу данных нескольким пользователям в одно и то же время на одной и той же частоте, сформировав для каждого из них индивидуальную ДН. Данная технология называется MU-MIMO и в настоящее время активно внедряется (а где-то уже) в системы связи. Возможность пространственного мультиплексирования предусмотрена, например, в стандарте мобильной связи 4G LTE, Wi-Fi стандарте IEEE802.11ay, стандартах мобильной связи 5G.
Виртуальные антенные массивы для радаров
Цифровые антенные решётки позволяют с помощью нескольких передащих антенных элементов сформировать для обработки сигнала виртуальную антенную решётку существенно больших размеров. Виртуальная решётка имеет все характеристики реаль��ой, однако для своей реализации требует меньших аппаратных затрат.
Оценка параметров источников излучения
Адаптивные антенные решётки позволяют решать задачу оценки числа, мощности, угловых координат источников радиоизлучения, устанавливать статистическую связь между сигналами различных источников. Главным достоинством адаптивных антенных решёток в этом вопросе является способность к сверхразрешению близкорасположенных источников излучения. Источников, угловое расстояние между которыми меньше ширины главного лепестка диаграммы направленности антенной решётки (предел разрешения Релея). Главным образом это становится возможным за счёт векторного представления сигнала, известной сигнальной модели, а также аппарата линейной математики.
Спасибо за внимание