Comments 101
Когнитивная психология давно исследует проблему происхождения чисел, счета и математики в целом, и установила, что их общим основаниям является чувство численности, кот. имеется уже у животных. В последние годы к этому добавились нейрофизиологические поиски нейронного коррелята этого чувства, кот. увенчались открытием «нейронов числа» в мозге. В дополнении к этому было произведено нейросетевое моделирование процесса возникновения чувства числа, как было установлено оно возникает спонтанно в результате обучения распознаванию зрительных сцен. Подробности можно посмотреть в этой статье, там имеются ссылки на оригинальные исследования. Можно утверждать, что результаты этих исследований (имеются и другие) являются аргументом в поддержку теоретико-множественного основания математики, хотя бы в наивной форме. Конечно требуется произвести подобные исследования, и нейросетевое моделирование, для понимания происхождения арифметических операций, геометрических примитивов и тд, и только тогда можно пытаться понять, как возникла абстрактная математика, основанная на обобщении этих базовых сенсорных примитивов.
Вы не исключаете сравнение, как важную, познавательную операцию мозга, на основе которой происходят математические вычисления?
Вы не исключаете сравнение, как важную, познавательную операцию мозга, на основе которой происходят математические вычисления?Да, конечно, если иметь в виду абстрактное мышление, вероятно, это одна из первых категорий, кот. появилась. Но основывается она на интуитивном понимании, механизм которого кроется в чувстве численности (в этой, несколько устаревшей, презентации можно посмотреть о чем речь). Оно присуще и животным, и детям, кот. не знают, что такое число, счет, и не могут, в общем случае, произвести точное сравнение двух совокупностей. В исследовании, ссылку на кот. давал, дополнительно установили, что это чувство подчиняется психофизическому закону Вебера-Фехнера (на wiki), кот. описывает связь интенсивности ощущений (проявлений чувства определенной модальности, это субъективные состояния, т.е. оно дано вам непосредственно в восприятии) с величиной физического воздействия. Эта связь нелинейная — логарифмическая, в реальности дискретная, разбитая порогами различения на отдельные интервалы, в кот. интенсивность ощущения не меняются. Как это проявляется? Дети, кот. не имеют понятия о счете, если им показать кучи из 2-х и 3-х конфет, и попросить выбрать, то они выберут, как правило, большую кучу. Но если им показать кучу из 9-ти и 10-ти конфет, то они выберут практически равновероятно. Этот свойство психики давно известно маркетологам, они используют его при повышении цен. Как правило увеличение цены до 10% не вызывает у большинства людей отказ от покупки товара, т.к. часто они даже не замечают его. Чувство численности связано с нейронами числа, обнаруженными у животных и людей, активность кот. имеет вероятностное распределение с максимумом при определенном числе объектов в наборах, и чем это число больше, тем максимум активности меньше, а распределение более пологое. Наиболее статистически достоверная аппроксимация этой активности также соотв. закону В-Ф. То есть субъективные ощущения не расходятся с соответствующей нейронной активностью, и возможно напрямую определяются ей. Это также подтвердилось моделирование нейросетями. Возможно на животных можно произвести эксперименты, действуя напрямую на активность этих нейронов, и заставлять их, например, делать выбор маленькой кучи приманки, а не большой, в противоречии с обычным поведением)
Откуда следует, что при делении на нуль «уничтожается мера»? До этого момента в рассуждении было нечто похожее на логику, но этот тезис взялся совершенно ниоткуда.
Из расчёта на то, что существует сама по себе операция деления, которая при сопоставлении делителя и делимого меняет представление в результате.
Это предложение синтаксически корректно, но смысл его от меня ускользает. Что значит «сама по себе»? Вначале было слово, и слово было «операция деления»? И что значит «меняет представление о результате»? Меняет относительно чего? У нас уже было какое-то представление о результате, а потом появилось деление и этот смысл изменило?
Конечно. Представим, что мы делим тот самый слиток на половину. Получаем в результате половину слитка. Суммируя половину слитка с полноценной, единственной копией того самого получим, как бы, полтора слитка (в качестве меры — единственный слиток). Меняем представление. Представляем расчёт в половинах того слитка: получаем 3 половины слитка в результате. Сама операция деления подразумевает сравнение (во сколько раз). На основании такого сравнения деление числа на ноль уничтожает меру, ведь сравнения нет самого по себе. Точнее, сравнение с пустотой подразумевает отсутствие сравнения, то есть уничтожение меры (которая появляется благодаря сравнению).
Но мера — это не свойство объекта. Это свойство нашего представления об объекте. С этой точки зрения пустота «типизирована», и отсутствие серебряного слитка не тождественно отсутствию, скажем, совести. Если у нас в какой-нибудь физической формуле вылезет нуль, это не значит, что джоули могут внезапно превратиться в килограммы.
Если мера не является свойством объекта, то почему вы не можете сопоставить вообще все объекты друг с другом по любому параметру? Почему они не однородны, как при сложении обычных чисел без мер? Отсутствие серебряного слитка не тождественно отсутствию, скажем, совести. Это так. Но это же выступает и за принадлежность конкретной меры конкретному объекту. А вот переход энергии в массу уже не кажется таким уж невероятным явлением сейчас. Вообще говоря, масса является ключевым параметром всех осязаемых тел. Другое дело, что она в разных условиях разная. Вы же не станете отрицать гравитационную постоянную и её значения на разных планетах (а уж тем более изменение)?
О, вы вернулись. Отлично. Я как раз заготовил пример, боялся, что он пропадёт зря.
Один и тот же серебряный слиток может являться мерой веса, мерой длины, мерой электрического сопротивления или мерой стоимости. В нём самом не содержится информации о том, в каком именно качестве он будет использоваться в нашем измерении, эта информация есть только в голове у измеряющего.
Один и тот же серебряный слиток может являться мерой веса, мерой длины, мерой электрического сопротивления или мерой стоимости. В нём самом не содержится информации о том, в каком именно качестве он будет использоваться в нашем измерении, эта информация есть только в голове у измеряющего.
Вспомнился Маркс. Тем не менее, нельзя, видимо, отделять информацию от самого материального объекта. Они друг друга дополняют. Прочтите Лоренца. Он прекрасно сопоставляет «чистый разум» и «опытное познание», ведь сам разум формируется под влиянием среды, в которой фиксируются объекты познания. Потому идея (информация) и сама материя неразрывны.
Почему же нельзя? Можно и нужно. Современная система мер физических величин как раз и есть результат такого отделения. Ну, то есть, понятно, что эти меры так или иначе относятся к объектам реального мира. Но — не к какому-то конкретному объекту (это особенно верно сейчас, когда упразднены эталоны из палаты мер и весов).
Соответственно, когда исчезает объект, мера не исчезает следом за ним. Соответственно, никакого исчезновения меры при делении на нуль не происходит.
Соответственно, когда исчезает объект, мера не исчезает следом за ним. Соответственно, никакого исчезновения меры при делении на нуль не происходит.
Вы сами же писали о противоречии и теперь в самом сообщении допускаете противоречие себе же. Вроде как можно отделить, но понятно что нельзя полностью. Прекрасно. Допустим я уничтожил эталон в Париже. Что будет новым эталоном? Схожий объект, но не тот. Я напоминаю что с абсолютной точностью, которую ни один математик в глаза не видел в действительности, нельзя сравнить два объекта. А вы думали ради чего проводились расчёты изменения эталона массы, которая, благодаря возгонке, уменьшается (у эталона)?
Вы сами же писали о противоречии и теперь в самом сообщении допускаете противоречие себе же.
Где именно я писал о противоречии? Ссылочку, пожалуйста.
Допустим я уничтожил эталон в Париже. Что будет новым эталоном?Вы точно со мной спорите? Я как раз писал о том, что сейчас эталоны в Париже стали не нужны. Все основные единицы измерения выражены тем или иным образом через физические константы. Вот, например, текущее определение килограмма.
Да. Ошибся. Тем не менее, противоречие в том, что вы не можете полностью избавиться от информации в содержании объекта. Вообще. Иначе, все объекты воспринимались бы однородно и были бы однородны (или вообще не воспринимались бы), ведь восприятие человека сформировано средой при отборе, с ориентиром на саму среду. А она ведь не однородна в восприятии.
Откуда взята постоянная? Разве не привязана к первому объекту выбора? Нет?
Это я ещё не спрашиваю вас про способ хранения «константы», который может быть подвержен износу (то есть изменяться).
Ну, то есть, понятно, что эти меры так или иначе относятся к объектам реального мира. Но — не к какому-то конкретному объекту.
Откуда взята постоянная? Разве не привязана к первому объекту выбора? Нет?
Это я ещё не спрашиваю вас про способ хранения «константы», который может быть подвержен износу (то есть изменяться).
Все ключевые физические величины сейчас определены не с помощью каких-то объектов, а с помощью экспериментов, которые можно провести где угодно
Все ключевые физические величины сейчас определены не с помощью каких-то объектов
Эксперименты на основе чего? Совсем без объектов? Что же это за эксперименты такие? Мысленные?
Не с помощью свойств конкретных объектов, как было с эталонами, а с помощью свойств объектов определенного класса, доступных теоритически в любой точке Вселенной. Вот надо измерить длину объекта — измеряем за сколько периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 свет вдоль этого объекта проходит в вакууме, делим на 9 192 631 770 и умножаем на 299 792 458 — получаем длину в метрах. И не нужны никакие конкретные эталоны.
основного состояния атома цезия-133 свет вдоль этого объекта
Значит объекты есть. Более того, измерение точное лишь в определённой степени.
Классы сами по себе не появились из неоткуда, а являются лишь абстракцией действительности, при поставленном условии. Пожалуйста, сообщите как получают в современности меру массы?
Точных измерений не бывает. Это я как (почти) инженер по измерительной технике знаю.
Суть революции измерений, проходящей сейчас, в том, что вместо конкретных объектов-эталонов используется любой объект определённого класса. Любой атом цезия-133 является эталоном, любой свет в вакууме, если мыслить терминами эталонов.
Килограмм пока тот же, что с 1889 года, но Международный комитет мер и весов рекомендовал заменить его на "эталон", основанный на фундаментальных свойствах материи.
Прекрасно. Буду ждать их попыток обойти свои мутные положения. Благодарю вас.
Нет, и килограмм уже не тот.
XXVI Генеральная конференция по мерам и весам (13—16 ноября 2018 года) одобрила определение килограмма, основанное на фиксации численного значения постоянной Планка. Решение вступило в силу 20 мая 2019 года.
Пропустил… Спасибо
Прекрасно. Благодарю. «Эталон» был, есть и будет.
Какой?) Что вы понимаете под эталоном?
P. S. Никто здесь (в этой ветке и ветках рядом) не отрицает существование единиц измерения и их пользы. Работа с ними тривиальна и почти не отличается от работы с обычными числами. Каких-то специальных теорий для этого не нужно.
P. S. Никто здесь (в этой ветке и ветках рядом) не отрицает существование единиц измерения и их пользы. Работа с ними тривиальна и почти не отличается от работы с обычными числами. Каких-то специальных теорий для этого не нужно.
Какой?)
Разумный.)
Что вы понимаете под эталоном?
Выбранный объект для измерения и сопоставления.
А вы что?
Каких-то специальных теорий для этого не нужно.
А вы откуда знаете? Математики, например, во времена Лобачевского не знали, когда понадобится его теория. Или понадобится она вообще.
Но его теория была проработанной.
Конечно всегда есть инструмент, которым непосредственно измеряют. Но при этом теперь (с весны этого года, когда стандартизировали килограмм) настройка этого инструмента не зависит от свойств какого-то материального объекта. Только от фундаментальных постоянных. Сегодняшняя наука признаёт их равными и постоянными во всей Вселенной. Предыдущее предложение означает не просто наличие такого мнения, но и проведённые эксперименты, которые с достаточной степенью уверенности подтверждают это.
Мне кажется, что ни один из комментаторов просто не понял, как пользоваться вашими скобками (да и вы сами ошибались). О чём можно говорить дальше — совершенно непонятно. Вы придумали что-то, но при этом не можете понятно объяснить что это и как этим пользоваться другим.
Лично мне непонятно следующее (кроме правил использования скобок) — вы говорите в тексте статьи о «мере», но представляете эту меру числами. Почему? Мера это ведь не про то, что в 1 м ровно 100 см. Это про единицы измерения. Как их можно у вас отличить?
Плюс к этому, вам уже отмечали, что используя вашу теорию получаются противоречивые результаты. Разве так можно?
Конечно всегда есть инструмент, которым непосредственно измеряют. Но при этом теперь (с весны этого года, когда стандартизировали килограмм) настройка этого инструмента не зависит от свойств какого-то материального объекта. Только от фундаментальных постоянных. Сегодняшняя наука признаёт их равными и постоянными во всей Вселенной. Предыдущее предложение означает не просто наличие такого мнения, но и проведённые эксперименты, которые с достаточной степенью уверенности подтверждают это.
Мне кажется, что ни один из комментаторов просто не понял, как пользоваться вашими скобками (да и вы сами ошибались). О чём можно говорить дальше — совершенно непонятно. Вы придумали что-то, но при этом не можете понятно объяснить что это и как этим пользоваться другим.
Лично мне непонятно следующее (кроме правил использования скобок) — вы говорите в тексте статьи о «мере», но представляете эту меру числами. Почему? Мера это ведь не про то, что в 1 м ровно 100 см. Это про единицы измерения. Как их можно у вас отличить?
Плюс к этому, вам уже отмечали, что используя вашу теорию получаются противоречивые результаты. Разве так можно?
Но его теория была проработанной.
Остроградский так не считал.
Предыдущее предложение означает не просто наличие такого метода, но и проведённые эксперименты, которые с достаточной степенью уверенности подтверждают это.
И это не исключает, по-прежнему, «выбранной единицы» измерения.
Лично мне непонятно следующее (кроме правил использования скобок) — вы говорите в тексте статьи о «мере», но представляете эту меру числами. Почему?
Потому что у мер есть масштаб (вы же выделяете в килограмме граммы). Разве вы можете сравнивать неоднородные меры (массу и протяжённость) друг с другом? Но я и не исключаю наличия в тех же скобках, собственно, самой меры (сущности, как кто-то отметил). Есть теория, что материя переходит в энергию. Так как разбор проходил над неотрицательными, действительными числами, то и необходимости касаться остального не было.
Плюс к этому, вам уже отмечали, что используя вашу теорию получаются противоречивые результаты.
Спрашивал, а в ответ, как правило, лишь вопросы. Так какие противоречивые результаты?
Я, правда, надеюсь, что у вас нет проблем со зрением. Вот этот комментарий 
А в чём проблема с единицами измерения? Они действительно нужны, но их выбор ни на что не влияет. Скорость всегда будет измеряться в единицах длины, делённых на единицы времени.
И понятно, что чтобы работать с величинами их приводят к одинаковым единицам измерения. Так в чём новшество вашей теории? Что она даёт полезного?
А в чём проблема с единицами измерения? Они действительно нужны, но их выбор ни на что не влияет. Скорость всегда будет измеряться в единицах длины, делённых на единицы времени.
И понятно, что чтобы работать с величинами их приводят к одинаковым единицам измерения. Так в чём новшество вашей теории? Что она даёт полезного?
Вот этот комментарий
После данного комментария что было написано в ответ мной? И это «противоречие»? Удивительно.
Так в чём новшество вашей теории? Что она даёт полезного?
Это не «Моя Теория» (каждый второй любит громкие слова). Вывожу взаимосвязь между мерой и величиной. Вывожу основу в виде сравнения, через которую происходит счёт и арифметика. Исходя из этого, делаю определённые выводы.
А в чём проблема с единицами измерения? Они действительно нужны
Какое тонкое наблюдение.
но их выбор ни на что не влияет.
Влияет на представление и вывод величин. Вот даже представим, в идеальном случае, что фрукт содержит в себе пять абсолютно одинаковых долек (более ничего нет). Предложение измерять фрукт в дольках даёт одни величины, предложение измерять фрукт в половинах долек (симметричных) даст другие. А вот предложение поделить фрукт на семь равных частей создаёт уже проблемы в представлении (и точности). Более того, с чего бы подчинять определённые меры исключительно десятичной системе счисления, ведь они для разных объектов могут иметь более удобные представления?
Все, конечно, привыкли к текущим установка, но кто решил, что это не вредит даже самой точности (измерениям)? А ведь по мере накопления научного материала погрешность может расти. Как бы учёные далее не подбирали постоянные, их могут привести в тупик накопленные установки прошлого. Но это так, мысленный вариант.
Скорость всегда будет измеряться в единицах длины, делённых на единицы времени
С фундаментальными "эталонами" могут получиться интересные эффекты с размерностями, грубо говоря, поделив метры на секунды, получим отношение числа Планка к гравитационной постоянной с каким-то коэффициентом
Вот к чему приводит ситуация, когда мозг работает, а знания в него не поступают или поступают в недостаточном количестве.
Подобно тому, как в какое-то время люди решили ввести комплексные числа, для решения кубических уравнений
Ну вы так-то и квадратное уравнение без комплексных чисел не решите...
С чего бы? Прекрасно решается квадратное уравнение над полем вещественных чисел.
А что корней может быть меньше двух – что такого? Над множеством кватерниов, например, у того же уравнения может быть бесконечное множество решений – так что теперь, считать, что два комплексных корня – мало?
Я согласен, но я имел ввиду, что в простейшей ситуации хотелось бы, чтобы полиномы степени n над полем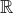 
имели ровно n корней (учитвая кратность). Для этого вам нужно искать и комплексные корни начиная уже с n = 2, даже если исторически впервые комлексные числа потребовались для решения кубических уравнений.
Насколько я помню историю математики, появление комплексных чисел было мотивировано кубическими уравнениями. А именно: при решении по формуле Кардано в промежуточных вычислениях могли появляться корни из отрицательных чисел. Но если с ними обращаться как с «нормальными числами», после сокращения они давали вполне себе действительные решения. И тут все задумались.
Слышал убедительную версию (аргументов не вспомню), что умножение появилось не как множественное сложение, а как площадь прямоугольника. Настоящая таблица Пифагора начинается с 1, а не с 2. Умножение на 1 как-то практически бессмысленно, а вот получение площади прямоугольника одна из сторон которого равна 1 единице — нет.
Исходя из этого, деление скорее всего появилось гораздо раньше. Собственно даже животные занимаются делением, когда, например, нужно накормить нескольких детёнышей. Понятно, что они не считают в нашем понимании, но фактически делят.
С таким подходом к делению деление на ноль уничтожает не "переменную", а необходимость её существования, необходимость всех предшествующих операций — незачем добывать, тащить добычу к детёнышам и делить, если детёнышей нет.
Да. Потому, исходя из невозможности сравнения, отсутствует сама по себе мера, но для наличия результата, при обратной операции, я сохранял в квадратной скобке величину.
Вот за последний абзац так чётко "приземляющий" математику, что так ценно в её объяснении людям не искушенным, хотел поставить +1, но не имею такой возможности… тоже своего рода деление на ноль, произведённое некогдА Хабром над созданным логином :)
можно ввести особую разновидность чисел для решения проблемы возврата значения при делении и умножении на ноль
Чем тут не подходят бесконечно малые? Нужно же отличать ноль как литерал от "актуального нуля" — величины, которая при добавлении к другой её не меняет, но не является литеральным нулём. Бесконечно малые типа dx — и есть актуальные нули.
Делить на литеральный ноль — нельзя и точка. Делить на актуальный ноль — можно, по правилам дифференциального исчисления.
Нужно заметить, что бесконечно малые в классическом анализе — вообще не числа. А "дэ икс" в, например, известном "дэ игрик по дэ икс" — так даже и не бесконечно малая.
(Есть, правда, нестандартный анализ, где бесконечно малые действительно числа, но он хоть и может показаться на первый взгляд простым и интуитивно понятным, на самом деле очень сложная конструкция. Лучше без необходимости её не привлекать.)
Вообще не спорю.
Именно что мне кажется, что автор предлагает "ad hoc, informally-specified and bug-ridden implementation" каких-то базовых дифференциалов. А проблема в дифференциальном исчислении решена для гораздо более общего случая, только в школе это не преподают — потому что когда по роду деятельности не нужно регулярно делить и умножать на ноль, то правило "на ноль делить нельзя" совершенно достаточно.
Проблема в пределах, которые устанавливают вместе с собой неопределённость. О неопределённости сообщил в концовке, для полноты.
Пределы как раз говорят, что делать с этой неопределённостью.
Вот у вас — 0/0 эквивалентно sin(15x)/(cos(x) — 1) при x=0? А почему?
И при этом возникает вопрос достижения самих значений (если опираться на определение того же Коши, то разница по модулю между значениями сама по себе не определена (есть условие, но нет значения)).
Тригонометрических величин не касался. Касался лишь целых, положительных чисел. Причины в публикации.
Тригонометрических величин не касался. Касался лишь целых, положительных чисел. Причины в публикации.
А у вас не возникает вопрос достижения самих значений? 5*0 или 3*0 — у вас тоже разные нули, почему они более систематически отражают действительность, чем 5dx и 3dy?
Если бы человек каждый раз пытался «достигать» простейших значений, при подсчёте мешков зерна, то он бы, очевидно, умер с голоду.
Нули разные при различных условиях. При 5 * dx, dx != 0. В ряде натуральных чисел 0 имеет чёткое место, а в пределе к нему лишь «стремятся» (ориентация на значение, которое к нему приближается, а не на сам 0).
Нули разные при различных условиях. При 5 * dx, dx != 0. В ряде натуральных чисел 0 имеет чёткое место, а в пределе к нему лишь «стремятся» (ориентация на значение, которое к нему приближается, а не на сам 0).
Ну, насчёт бесконечности вы правы, а вот с нулём загнули. Утверждение «в моей крови нулевое содержание ТГК» имеет смысл, и, используя терминологию автора, единицы измерения важна — нельзя просто сказать «в моей крови нулевое содержание».
Когда-то математики "оцифровали" нулём понятие — констатацию отсутствия чего-либо, но потом пришлось уточнять, что отсутствия не абсолютного, но в части какого-то параметра, измеряемого одной из Единиц Системы Мер.
Вот теперь ещё и пытаются вспомнить что именно отсутствовало первоначально ;))
>> Имея наблюдаемый пример, в котором мы позволяем себе поделить на ноль какое-то слагаемое, мы просто избавляем пример от этого слагаемого
Не совсем понятно. Умножая на ноль, мы действительно избавляемся от чего-нибудь. А вот когда делим…
Деление даёт соотношение, то есть чистое число, без меры, но это если мы делим на такую же сущность. Так же мы можем делить на число, то есть на меру, и тогда опять получаем сущность, а не число. Умножение даёт новую сущность с той же мерой, что и у старой, хотя и здесь можно вспомнить, например, возведение в квадрат, когда мы сущность умножаем на сущность и получаем… непонятно что.
Но деление на ноль должно давать некое число, если 0 — сущность, и давать некую сущность, если 0 — число, но оно никак не может приводить к избавлению от числа либо сущности.
Так же стоит заметить, что математика часто избавляется от полезной информации (то есть не только при умножении на ноль). При целочисленном делении получаем a/b=c+r, то есть результат содержит два числа — частное и остаток. Точно так же могло бы быть при умножении на ноль — a*0=0\a, где \a есть указание на информацию о начальном состоянии данного нуля (до умножения). Ещё пример — при возведении -1 в степень мы теряем количество умножений, а вместе с ним и знак после выполнения обратной операции, хотя если бы информацию сохраняли, то могло бы быть что-то вроде такого: -1^2=1\-2, где минус и двойка показывают знак перед возведением и количество умножений. Аналогично синус от x+360 стирает информацию о начальном угле, которая так же могла бы помочь при вычислении арксинусов. То есть проблема потери информации повсеместна в математике, а отсюда следует множество усложнений, вроде комплексных чисел, которые призваны устранять неопределённость, цепляя к результату все возможные состояния числа до выполнения операции. Хотя с другой стороны, часто просто нет возможности получить информацию о начальном состоянии, например принимая некий сигнал от звёзд, мы вряд ли сможем слетать и проверить, сколько раз ихний синус был обёрнут вокруг 360 градусов. Но в некоторых случаях информация всё же есть, а потому есть и смысл в её сохранении с целью устранения неоднозначности после выполнения обратных операций. К сожалению, эту тему (по полноте сохранения информации) в математике полностью игнорируют. Хотя в приложениях математики вполне можно встретить что-то вроде «здесь была минус единица, значит после такого преобразования будет не плюс-минус, а строго один знак». Но это всё несистемно, без теоретической базы, чисто на глаз, кому как взбредёт в голову.
Не совсем понятно. Умножая на ноль, мы действительно избавляемся от чего-нибудь. А вот когда делим…
Деление даёт соотношение, то есть чистое число, без меры, но это если мы делим на такую же сущность. Так же мы можем делить на число, то есть на меру, и тогда опять получаем сущность, а не число. Умножение даёт новую сущность с той же мерой, что и у старой, хотя и здесь можно вспомнить, например, возведение в квадрат, когда мы сущность умножаем на сущность и получаем… непонятно что.
Но деление на ноль должно давать некое число, если 0 — сущность, и давать некую сущность, если 0 — число, но оно никак не может приводить к избавлению от числа либо сущности.
Так же стоит заметить, что математика часто избавляется от полезной информации (то есть не только при умножении на ноль). При целочисленном делении получаем a/b=c+r, то есть результат содержит два числа — частное и остаток. Точно так же могло бы быть при умножении на ноль — a*0=0\a, где \a есть указание на информацию о начальном состоянии данного нуля (до умножения). Ещё пример — при возведении -1 в степень мы теряем количество умножений, а вместе с ним и знак после выполнения обратной операции, хотя если бы информацию сохраняли, то могло бы быть что-то вроде такого: -1^2=1\-2, где минус и двойка показывают знак перед возведением и количество умножений. Аналогично синус от x+360 стирает информацию о начальном угле, которая так же могла бы помочь при вычислении арксинусов. То есть проблема потери информации повсеместна в математике, а отсюда следует множество усложнений, вроде комплексных чисел, которые призваны устранять неопределённость, цепляя к результату все возможные состояния числа до выполнения операции. Хотя с другой стороны, часто просто нет возможности получить информацию о начальном состоянии, например принимая некий сигнал от звёзд, мы вряд ли сможем слетать и проверить, сколько раз ихний синус был обёрнут вокруг 360 градусов. Но в некоторых случаях информация всё же есть, а потому есть и смысл в её сохранении с целью устранения неоднозначности после выполнения обратных операций. К сожалению, эту тему (по полноте сохранения информации) в математике полностью игнорируют. Хотя в приложениях математики вполне можно встретить что-то вроде «здесь была минус единица, значит после такого преобразования будет не плюс-минус, а строго один знак». Но это всё несистемно, без теоретической базы, чисто на глаз, кому как взбредёт в голову.
Получающиеся «памятные числа» не могут взаимодействовать с другими числами посредством арифметики, хотя должны взаимодействовать друг с другом, в силу наличия одинаковых мер, но это уже устанавливает сам вычисляющий. … Другое дело, что числа одномерны, при использовании сами по себе.
Вот в связи с этим возникает вопрос — что делать при более сложных вычислениях? Работает ли для ваших чисел ассоциативность (сложения и умножения), коммутативность, дистрибутивность?
Ну то есть из последнего предложения следует, что можно взять вещественные числа, заключить их в скобки, добавив к ним меру 1, и использовать как «памятные». Особенно интересны нетривиальные примеры, в которых будет использоваться деление и умножение на ноль.
Это должно зависеть от сопоставления мер. Рассмотрим нашу реальность. Нам ничто не мешает умножать литры на кубические метры. И вот тут возникает вопрос — в чём целесообразность? Потому возможность ассоциативности (сложения и умножения), коммутативности, дистрибутивности отвергается или принимается исходя из наблюдаемого опыта. Сама математика — это результат наблюдаемого опыта, который обработан мозгом. Определение условий восприятия напрямую влияет лишь на форму, но не содержание результата. Благодаря подобному «2 * 2 != 4 в поле вычетов по модулю три» («Кризис научного познания» Сарданашвили).
Подождите, я говорю об одной мере у всех чисел. А вы зачем-то предлагаете складывать литры и метры. Кроме внутренней противоречивости, которую отметили ниже, наверняка есть ещё куча проблем. То есть зачем обычно создают новый мат аппарат? Чтобы упростить вычисления. А что можно вычислить с помощью вашей системы, кроме каких-то простых примеров. В половине которых получается тот результат, который приятен вам.
В поле вычетов по модулю три 4 = 1, как и результат 2 * 2. Там всё в порядке.
В поле вычетов по модулю три 4 = 1, как и результат 2 * 2. Там всё в порядке.
А в чём внутренняя противоречивость?
Я не предлагал складывать, а лишь указал на возможность этого. Это была аналогия на ваши предыдущие вопросы.
С помощью «Моей Системы» (слишком громкие слова для какого-то пользователя сети (меня)), можно попробовать посмотреть на данную проблему с определённой точки зрения. Вам решать как к этому относиться.
Я не предлагал складывать, а лишь указал на возможность этого. Это была аналогия на ваши предыдущие вопросы.
С помощью «Моей Системы» (слишком громкие слова для какого-то пользователя сети (меня)), можно попробовать посмотреть на данную проблему с определённой точки зрения. Вам решать как к этому относиться.
Вы могли бы показать практический пример, когда такой подход упрощает жизнь.
Есть мнение, что это может найти применение в теории систем и измерений, о которых автор имеет некоторое представление, но чтобы не ошибиться, лучше промолчать.
В начале поста вы жаловались на то, что математика, дескать, оторвана от реальности. Однако она приносит пользу. Если ваш подход не приносит пользу (по крайней мере, нет свидетельств в пользу этого) — возможно, он ещё больше оторван от реальности?
Не надо выставлять желаемое за действительное. Это не жалоба, а факт. Если вы в состоянии математически вывести общее уравнение жидкости, то прошу вас. Польза в том, что при изменении условий системы её отдельные элементы могут складываться (вычитаться, умножаться или делиться). Условие является той самой мерой, по которой происходит сравнение. В самом примитивном представлении те же подключаемые элементы меняют общие параметры электрической сети, к которой они подключаются (или из которой отключаются).
1. Верно ли, что всё, с помощью чего нельзя вывести «общее уравнение жидкости» (я не знаю, что это, но ладно), оторвано от реальности?
2. Ваша теория позволяет вывести общее уравнение жидкости?
3. Покажите, какую пользу ваша теория может принести электрическим сетям. Какой-нибудь практический пример.
4. Кстати, я не помню, писал тут кто-то уже или нет, но ваши «числа с памятью» — плохо продуманный аналог гипервещественных чисел. Которые лишь чуть моложе моей бабушки, но до сих пор никому особо не пригодились.
2. Ваша теория позволяет вывести общее уравнение жидкости?
3. Покажите, какую пользу ваша теория может принести электрическим сетям. Какой-нибудь практический пример.
4. Кстати, я не помню, писал тут кто-то уже или нет, но ваши «числа с памятью» — плохо продуманный аналог гипервещественных чисел. Которые лишь чуть моложе моей бабушки, но до сих пор никому особо не пригодились.
1. Нет.
ru.wikipedia.org/wiki/Уравнение_Эйлера
И таких, различных уравнений несколько. Надо бы универсальное иметь. Общее.
2. Не знаю.
3. Сети могут обойтись простым расчётом суммы сопротивлений каждого проводника без «моей теории». И вы всё равно опираетесь на одинаковую меру (сопротивление в определённом исчислении (Ом)).
Могу намекнуть на использовании в программировании. Например, арифметика объектов лишь определённых, общих статусов (мер, положений) в зависимости от определяемых условий (опять же расчёт систем).
4. Рад за вашу бабушку. Когда-то и отрицательные числа никому были не нужны.
ru.wikipedia.org/wiki/Уравнение_Эйлера
И таких, различных уравнений несколько. Надо бы универсальное иметь. Общее.
2. Не знаю.
3. Сети могут обойтись простым расчётом суммы сопротивлений каждого проводника без «моей теории». И вы всё равно опираетесь на одинаковую меру (сопротивление в определённом исчислении (Ом)).
Могу намекнуть на использовании в программировании. Например, арифметика объектов лишь определённых, общих статусов (мер, положений) в зависимости от определяемых условий (опять же расчёт систем).
4. Рад за вашу бабушку. Когда-то и отрицательные числа никому были не нужны.
Намёк имеет смысл лишь при условии уверенности, что намекающий что-то знает. Я полагаю, что вы не знаете, как применить ваши чудо-числа в народном хозяйстве. Я полагаю, что так же полагает большинство читателей поста. Можете попробовать разубедить. Но если не захотите — не страшно.
Придумывать числовые системы легко. Мы с соседями по мехматовской общаге только за первый курс придумали штуки три. Вопрос именно в практической применимости. Пассы руками и околофилософские аргументы в этом плане не работают примерно со времён Пифагора.
Придумывать числовые системы легко. Мы с соседями по мехматовской общаге только за первый курс придумали штуки три. Вопрос именно в практической применимости. Пассы руками и околофилософские аргументы в этом плане не работают примерно со времён Пифагора.
Сдаётся мне, что вы тут под каждым ответом пытаетесь самоутвердиться. Только вот в чём проблема. Вы можете придумывать числовые системы с кем угодно и делать ставку на это, но в статье указывается на другое основание рассмотрения данного вопроса. А «чудо-числа» в хозяйстве применяются на автомате уже при том случае, когда сопоставляются разные величины разных мер (например килограммы и граммы). Вспомните понятие неправильной дроби. Для сопоставления дробей с разными знаменателями вы приводите их к общему. Если я сопоставляю дроби (хочу сложить, или вычесть) разных масс и с разными знаменателями, то я их подгоняю ведь под одну меру (и общий знаменатель), верно? Как с этим очевидным случаем поспорите? Что же я меняю, когда привожу к общему знаменателю, как не меру, сводя её к общей?
Давайте вы не будете строить догадки о моих мотивах. Иначе мы скоро придём к постановке диагноза по никнейму. Этот стиль ведения дискуссии не приличествует Хабру.
Килограммы с граммами прекрасно сопоставлялись и до появления вашего поста. Вообще, у меня довольно простой критерий «близости к реальности», и это — польза. Если некая мысленная конструкция пользу приносит, то она отражает какие-то важные свойства реальности. В противном случае это подсчёт ангелов на острие иглы. Какую пользу принесёт ваше понимание? Вы сначала говорили про электрические сети, затем про программирование. Ни там, ни там вы мне не дали конкретики. Теперь вы говорите, что весь мир и так пользуется вашей теорией, просто сам ещё этого не понял. Но если всё и так работает, опять же, в чём польза вашей теории?
Да, и вы так и не дали какого-то содержательного комментария по поводу сравнения с гипервещественными числами. Вам не кажется, что ваши «числа с памятью» — просто плохо продуманная версия гипервещественных чисел? Если так, не стоит ли признать, что вы изобрели колесо от велосипеда? Если не так, то чем ваши числа лучше?
Килограммы с граммами прекрасно сопоставлялись и до появления вашего поста. Вообще, у меня довольно простой критерий «близости к реальности», и это — польза. Если некая мысленная конструкция пользу приносит, то она отражает какие-то важные свойства реальности. В противном случае это подсчёт ангелов на острие иглы. Какую пользу принесёт ваше понимание? Вы сначала говорили про электрические сети, затем про программирование. Ни там, ни там вы мне не дали конкретики. Теперь вы говорите, что весь мир и так пользуется вашей теорией, просто сам ещё этого не понял. Но если всё и так работает, опять же, в чём польза вашей теории?
Да, и вы так и не дали какого-то содержательного комментария по поводу сравнения с гипервещественными числами. Вам не кажется, что ваши «числа с памятью» — просто плохо продуманная версия гипервещественных чисел? Если так, не стоит ли признать, что вы изобрели колесо от велосипеда? Если не так, то чем ваши числа лучше?
Давайте вы не будете строить догадки о моих мотивах.
Давайте не давайте. К чему была тогда биография? Мы её тут не касаемся.
Но если всё и так работает, опять же, в чём польза вашей теории?
Это не «моя теория». Это просто вывод на основании информации и сопоставления. Пользу ищет каждый сам.
Да, и вы так и не дали какого-то содержательного комментария по поводу сравнения с гипервещественными числами. Вам не кажется, что ваши «числа с памятью» — просто плохо продуманная версия гипервещественных чисел?
Их вообще не рассматривал и не ориентировался на пользу саму по себе. Сделал предположение, которое очевидно и исходит из очевидного. Возвращаясь к своим вопросам.
Если я сопоставляю дроби (хочу сложить, или вычесть) разных масс и с разными знаменателями, то я их подгоняю ведь под одну меру (и общий знаменатель), верно?
Значит, вы не можете обосновать пользу. И даже поленились ознакомиться с существующим решением, которое вам поднесли на блюдечке. Я услышал достаточно, спасибо за беседу.
Значит, вы не можете обосновать пользу.
Не согласен.
Я услышал достаточно, спасибо за беседу.
Вы прочли. Благодарю.
А ещё не ответили на последний вопрос. Вас что-то смутило? Почему?
Не согласен.Ваше несогласие не является аргументом. Обоснование являлось бы, но, полагаю, я его не услышу.
А ещё не ответили на последний вопрос.А что именно я должен на него ответить? В первой части статьи вы говорите правильные вещи. Правильные, потому что очевидные, просто сформулированные странным языком. Утверждение про «потерю меры» — это схоластика. «Числа с памятью» и далее — слабая попытка изобрести заново кусок существующего матана. Мой ответ достаточно полон?
Я не спрашиваю про части статьи.
В своих сопоставлениях, при том вопросе, я меняю меру (представление), чтобы провести действие с дробями? Да или нет?
В своих сопоставлениях, при том вопросе, я меняю меру (представление), чтобы провести действие с дробями? Да или нет?
Вы — наверное, меняете. Если вам удобнее представлять 3/5 как тройку, измеренную в пятёрках — кто я такой, чтобы вам запрещать?
Вы меняете тоже, только вам, видимо, нужна памятка из системы СИ, чтобы ориентироваться на принятые меры и безмерные величины.
Я — ни в коем случае. Я оперирую числами как формальной системой, одной из. Вы можете придать этому смысл манипуляции с мерами. Какой-нибудь гипотетический нумеролог может сказать, что я таким образом поклоняюсь, не знаю, Сатурну. Со своих точек зрения вы будете одинаково правы.
Но то, что вы написали, — ваша точка зрения. Значит, вы так же не далеки от указанного фанатика. Странно получается.
Ну вы тут какое-то ток-шоу устроили. Куда приглашают биохимика и гомеопата, а затем стараются выставить всё так, будто у них две равноправных точки зрения, а зрителю надо быть умнее и выше этого. Диалектически подходить к вопросу, так сказать.
Точки зрения не равноправны. Одни парадигмы продуктивны, другие нет. Парадигма, в которой воспитан я, доказала свою продуктивность.
Точки зрения не равноправны. Одни парадигмы продуктивны, другие нет. Парадигма, в которой воспитан я, доказала свою продуктивность.
Точки зрения не равноправны.
Это тоже мнение.
Веет каким-то догматом.
Парадигма, в которой воспитан я, доказала свою продуктивность.
Опять биографию включаете? Много «я».
ток-шоу
Разговорный показ? Странно получается.
Это тоже мнение.Ну, как говаривал товарищ Бэкон, опыт — критерий истины. С точки зрения голой логики механика Аристотеля не лучше и не хуже механики Ньютона.
Веет каким-то догматом.
Опять биографию включаете? Много «я».Отчего у вас такая болезненная на это реакция?
Разговорный показ? Странно получается.Вы никогда не слышали слово «ток-шоу»?
Ну, как говаривал товарищ Бэкон, опыт — критерий истины.
И он прав, только в его высказывании нет ничего о мнении. Вам подойдёт Гоббс. Цитату приводить не буду, ведь ваша установка
Отчего у вас такая болезненная на это реакция?
Не согласен. Мы же не вас обсуждаем.
Вы никогда не слышали слово «ток-шоу»?
Сочетание двух неоправданных, английских слов (у которых в русском есть переводы), написанных на кириллице, словом быть не может. Вы писали про пользу и даже тут себе же противоречите. Странно получается. Ну ладно. Я достаточно от вас (и о вас) узнал. Теперь моя очередь прощаться. Всего хорошего вам. А мне нужно продолжать убивать «чудовищ» (а не «драконов»).
И он прав, только в его высказывании нет ничего о мнении.Это только ваше мнение =)
Сочетание двух неоправданных, английских слов (у которых в русском есть переводы), написанных на кириллице, словом быть не может.Если вы такой знаток русского языка, то должны знать, что запятыми разделяются только однородные определения. А также — что язык динамичен, и его развитие не зависит от вашего представления о том, каким он быть должен. А ещё — что до правильности речи начинают докапываться тогда, когда нечего сказать по существу.
Всего хорошего вам. А мне нужно продолжать убивать «чудовищ» (а не «драконов»).Ну не обманывайте себя. Вы убиваете только время. А оно — вас. Всего хорошего. Можете ещё что-нибудь ответить, если вам критически важно оставить за собой последнее слово.
Это только ваше мнение =)
Это только факт. До меня это доказали уже Кант, Лоренц, ещё пару десятков нобелевских лауреатов, а так же сама действительность. Опровергните.
Если вы такой знаток русского языка, то должны знать, что запятыми разделяются только однородные определения. А также — что язык динамичен, и его развитие не зависит от вашего представления о том, каким он быть должен.
Как «знаток» русского языка, напоминаю про авторскую пунктуацию, дополнения и единую систему языка в которой, посредством однокоренных слов, формируется понимание их значений, что сразу создаёт ПОЛЬЗУ в экономии числа корней и их восприятии через ассоциативную связь.
Можете ещё что-нибудь ответить, если вам критически важно оставить за собой последнее слово.
Как бы я без вашего разрешения смог? Диво дивное.
К сожалению, автор попадает в ловушку "убийства дракона": пытаясь победить формализм исходя из соображений "реальности" и "практической полезности", он теперь вынужден создать новый формализм, причем по всем правилам. Без четкой аксиоматики, без доказательства того, что новая система является полем, использовать её наряду с числами нельзя. Кроме того, похоже, что в этой системе есть нетривиальные делители нуля, а значит, она полем не является, значит неизбежны проблемы с единственностью разложения на множители и сокращениями при делении. Самое же главное, дракон, с которым сражается автор, столь же нереален и далёк от практики, как и указанная в самом начале "проблема формальной математики". Даже сугубо реалистичной инженерной физике никогда не мешали ограничения, накладываемые на операции с числами теорией полей, а, напротив, помогали познавать и моделировать сущности. Анализ размерности — прекрасный инструмент инженера, теория групп — инструмент теорфизика, теория конечных полей, типов и категорий — инструмент программиста. Возможно, предлагаемый здесь формализм может стать одним из таких инструментов, но пока я вижу в нём больше противоречий (указанных уже комментаторами выше), чем может позволить себе теория.
К слову, если статья на математическую тему начинается с упоминания теоремы Гёделя о полноте, это сильный признак её нематематичности. А если она, к тому же, переключается на вопросы "практичности" математики, то материал, скорее всего, не интересен и не полезен.
Лучше оставить в покое Гёделя, и построить стройную непротиворечивую аксиоматику, с выводом основных положений, типа теоремы Безу, основной теоремы арифметики и т.п. А если уж так хочется "полезности", показать пример приложения новой системы за пределами возможностей уже известных.
Вы указали на противоречие, но не уточнили его. Какое именно?
К слову, о Гёделе упоминается ради указания на опытное начало любой аксиоматики. Само деление (да даже умножение) на ноль — это всё же положение взятое из опыта. Если вы вывели как-то умножение и деление на ноль исходя из каких-то других, опосредованных положений вашей (любой чужой) аксиоматики, то будет очень интересно увидеть это. Прошу. Заранее благодарю — тут к высказыванию Ницше никто не стремился.
К слову, о Гёделе упоминается ради указания на опытное начало любой аксиоматики. Само деление (да даже умножение) на ноль — это всё же положение взятое из опыта. Если вы вывели как-то умножение и деление на ноль исходя из каких-то других, опосредованных положений вашей (любой чужой) аксиоматики, то будет очень интересно увидеть это. Прошу. Заранее благодарю — тут к высказыванию Ницше никто не стремился.
Почему-то до 19 века математики прекрасно разрабатывали теорию без аксиом. Если вы не можете выделить понятие меры, которое не обязательно имеет математическую сущность, то это довольно странно.
Я не продвигаю, а вывожу взаимосвязь между мерой и величиной. Вывожу основу в виде сравнения, через которую происходит счёт и арифметика. Исходя из этого, делаю определённые выводы.
Ваши требования не будут удовлетворены уже по причине того, что сама математика (на текущее время) не может учесть всех проявлений действительности.
Ваши требования не будут удовлетворены уже по причине того, что сама математика (на текущее время) не может учесть всех проявлений действительности.
Более автор не будет иметь возможности отвечать на комментарии публикации. Тяжело бороться с «драконами» и выискивать «противоречия». Благодарю за комментарии. Задача выполнена, а это главное.
…Аркадий и Борис Стругацкие, «Понедельник начинается в субботу. Сказка для научных работников младшего возраста.»
Поэтому одни сотрудники все время занимались делением нуля на нуль на настольных «мерседесах», а другие отпрашивались в командировки на бесконечность. Из командировок они возвращались бодрые, отъевшиеся и сразу брали отпуск по состоянию здоровья. В промежутках между командировками они ходили из отдела в отдел, присаживались с дымящимися сигаретками на рабочие столы и рассказывали анекдоты о раскрытии неопределенностей методом Лопиталя. Их легко узнавали по пустому взору и по исцарапанным от непрерывного бритья ушам. За полгода моего пребывания в институте они дали «Алдану» всего одну задачу, которая сводилась все к тому же делению нуля на нуль и не содержала никакой абсолютной истины. Может быть, кто-нибудь из них и занимался настоящим делом, но я об этом ничего не знал.
представьте себе сейф с деньгами. Потом сейф без денег, пустой сейф. Имеет ли право на существование пустой сейф? Разве что как олицетворение понятия "деньги" как некий контейнер способный содержать и хранить в себе некоторое их количество ;)
Sign up to leave a comment.
Философия деления на… или исповедь сумасшедшего