Мы измерили вибрации маленького маятника на уровне одного нанометра. А потом засунули его в холодильник и охладили его до -250°C. А потом использовали квантовые корреляции, чтобы уменьшить шумы в системе и получше наблюдать сигнал.

Квантовые технологии помогают нам в самых разных областях. Например, когда нам нужно измерить очень слабый сигнал, а квантовые шумы в системе очень мешают. Это традиционная проблема, например, в гравитационно-волновых детекторах, в которых квантовые ф��уктуации в амплитуде и фазе лазера, используемого для измерения положения зеркал, мешают наблюдению гравитационных волн. Я об этом рассказывал в своей статье про детектор Einstein Telescope, который появится в Европе в недалеком будущем.
У нас в эксперименте получился маленький прототип этого детектора. Наша статья об этом эксперименте была опубликована в Physical Review Letters,
а препринт тут: Squeezed-light interferometry on a cryogenically-cooled micro-mechanical membrane.
В природе множество слабых сил, которые ученым очень хотелось бы изучить.
Проблема в том, что измерить силу напрямую мы не можем, а можем только наблюдать ее эффект на разные тела.
Самый простой и эффективный способ измерить силу — использовать маятник. Сила смещает маятник, и мы измеряем это смещение. Когда частота силы близка к резонансной частоте маятника, смещение оказывается значительно усиленным, и мы можем наблюдать хороший сигнал.
Чтобы измерять смещение маятника, удобно использовать свет. Когда мы светим лазером на маятник, покрытый отражающим веществом, фаза отраженного света содержит информацию о смещении маятника.
Фазу света напрямую мы наблюдать не можем, для этого нужен интерферометр.
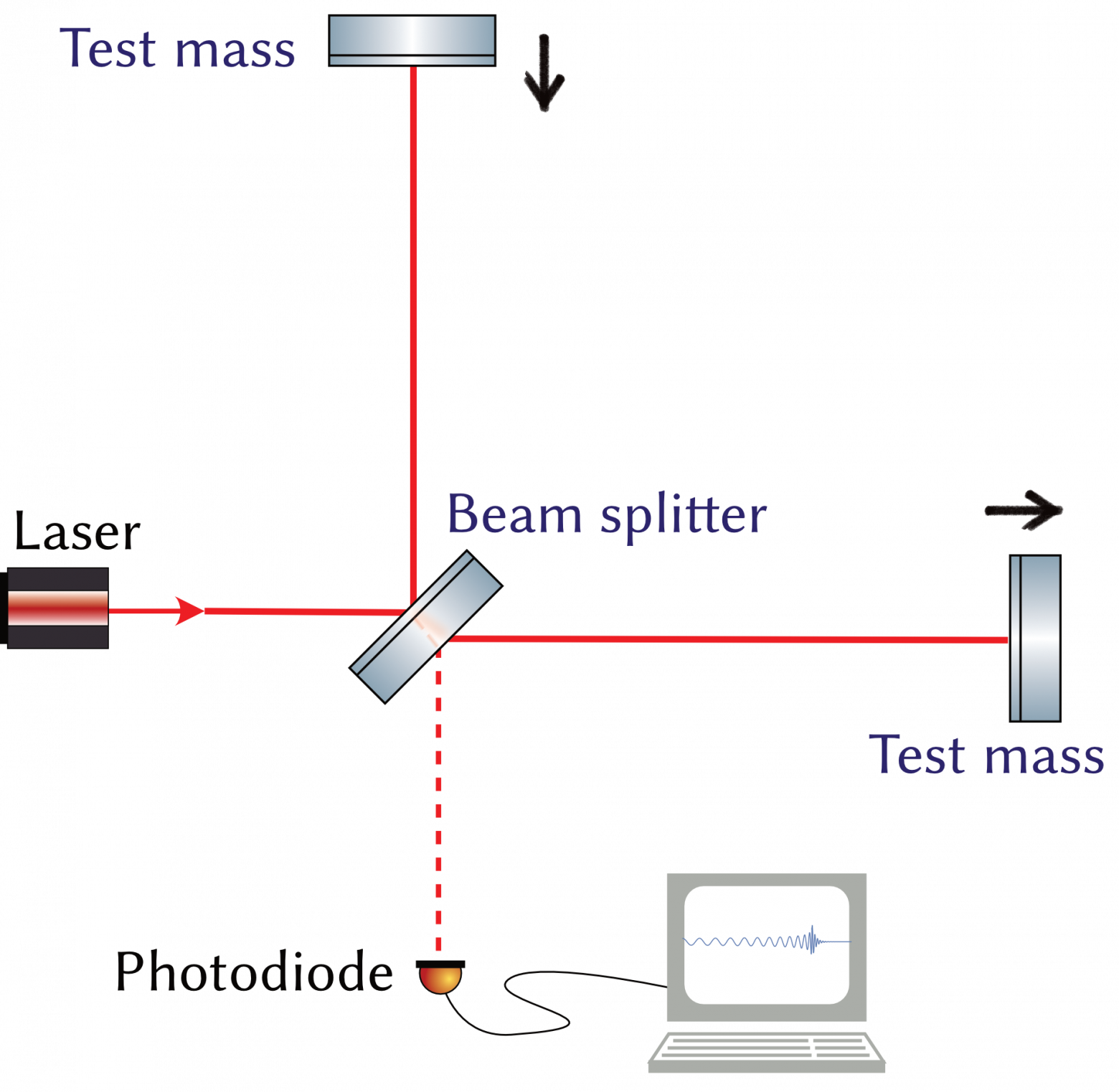
Интерферометр Майкельсона: лазерный луч делится два две равных части на делителе луча (beam splitter), отражается от подвижных зеркал, где приобретает фазу с информацией об их смещении. После возвращения на делитель луча, разные фазы луча интерферируют (амплитуды складываются или вычитаются), и на выходе мы видим сигнал, пропорциональный смещению зеркал.
На этом принципе работают не только детекторы гравитационных волн, но и большая часть сенсоров.
К сожалению, кроме сигнала в таком детекторе будет еще множество разных источников шума.
Про некоторые я писал в своей статье про детектор Einstein Telescope, а здесь ограничусь только двумя.
Представим маятник как зеркальце, подвешенное на нитке.
Тепловое броуновское движение молекул в этой нитке приводит возбуждает колебания зеркала. Это движение в принципе случайное и может быть представлено как сила действующая на зеркало на разных частотах. На частотах близких к резонансу маятника, эта сила приводит к резонансному увеличению смещения зеркала. И хотя спектр тепловой силы белый (т.е. сила одинаковая на всех частотах), при измерении спектра движения зеркала мы увидим характерный пик на резонансной частоте.
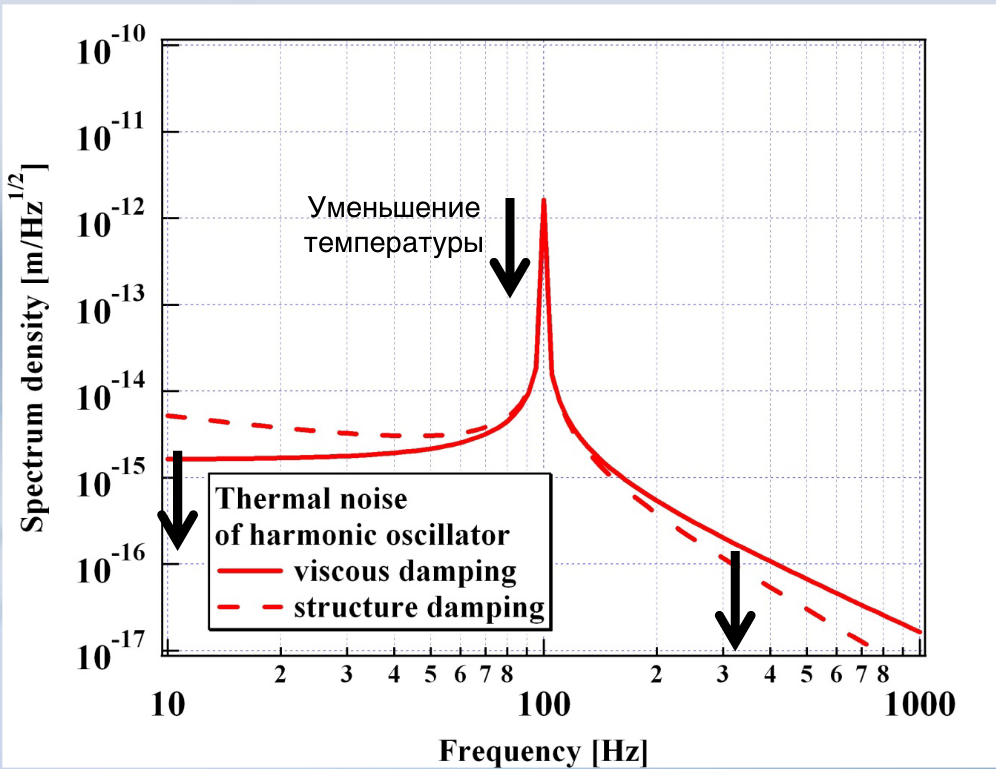
Спектр теплового шума: смещение маятника под действием теплового шума на разных частотах. Чем меньше температура, тем меньше шум. Украдено отсюда.
Тепловой шум зависит от температуры (чем ниже, тем меньше шум) и от качества нитки (количества потерь). Строго говоря, есть флуктуационно-диссипационная теорема, которая связывает наблюдаемый шум с диссипацией в системе.
Соответственно, в будущих детекторах гравитационных волн с этим шумом будут бороться двумя путями: охлаждением подвесов (и зеркал) и увеличением их качества. В нашем эксперименте мы наблюдали спектр теплового шума и уменьшали его с помощью охлаждения, но об этом ниже.
свет имеет квантовую природу, отдельные фотоны летят с разной случайной задержкой. Другими словами, фаза луча света оказывается случайной.
Когда мы пытаемся измерить фазовый сигнал от внешней силы, он оказывается ограничен этой фазовой неопределенностью. На детекторе мы видим шум белого спектра, который оказывается фундаментальным ограничением в точности измерений. Все детекторы ограничены дробовым шумом. Несмотря на его фундаментальность, можно использовать квантовые корреляции, чтобы снизить уровень этого шума.
Для этого нужно вспомнить немного квантовой механики. Неопределенность в фазе и неопределенность в амплитуде лазера связаны соотношением Гейзенберга:
В обычном лазерном луче эти неопределенности равны. Однако, можно сжать неопределенность в фазе за счет увеличения неопределенности амплитуды — главное, чтобы их произведение удовлетворяло соотношению неопределенности. Такой свет называется сжатым со степенью G:
Мы воспользуемся как раз таким трюком, и сожмем неопределенность в фазе, позволив улучшить наблюдение сигнала. Кстати, гравитационно-волновые детекторы уже используют сжатый свет для всех последних наблюдений. Мы еще недавно делали эксперимент, где игрались с этим сжатым светом, и я писал об этом на Хабре.
Итак, разобравшись с основами, перейду к эксперименту.
В нашем эксперименте мы использовали в качестве маятника маленькую мембрану со стороной в 1мм и толщиной в��его 50нм.

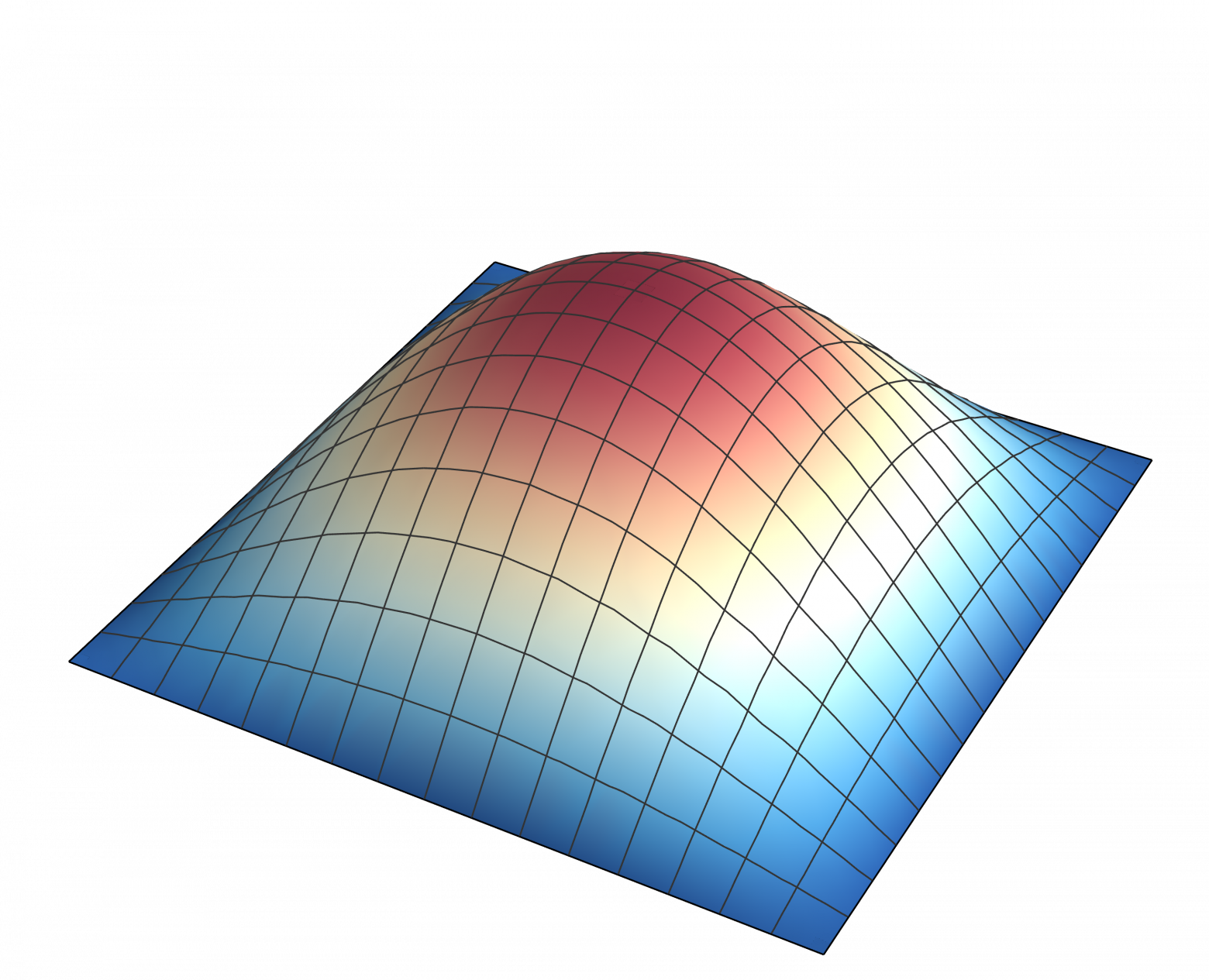
Слева: фотография мембраны (маленькое окошко в центре серой рамки). Мембрана натянута как барабан на рамку, и колеблется внутри. Справа: иллюстрация смещения мембраны.
Такая мембрана колеблется на частоте около 400кГц, и ее добротность (количество осцилляций до потери половины энергии) составляет порядка 105. Для этого, правда, приходится ее поместить в вакуум, иначе воздух давит на нее слишком сильно, и она не колеблется.
А еще она достаточно прозрачная: ее коэффициент отражения составляет всего 20%.
Это не очень удобно, потому что если использовать такую мембрану в интерферометре Майкельсона, большая часть сигнала будет потеряна. Хуже того, когда мы захотим использовать сжатый свет, эти квантовые корреляции тоже потеряются, а они особенно чувствительны к потерям. Так что мы решили использовать другую конфигурацию интерферометра, «сложив» два плеча интерферометра Майкельсона так, что два зеркала оказались одним — нашей мембраной.
В таком интерферометре есть две моды: часть света проходит сквозь мембрану, и просто выходит из интерферометра, не неся никакого сигнала (это мода Саньяка). Другая часть отражается и приобретает фазу, пропорциональную смещению мембраны, и мы получаем сигнал на выходе интерферометра.
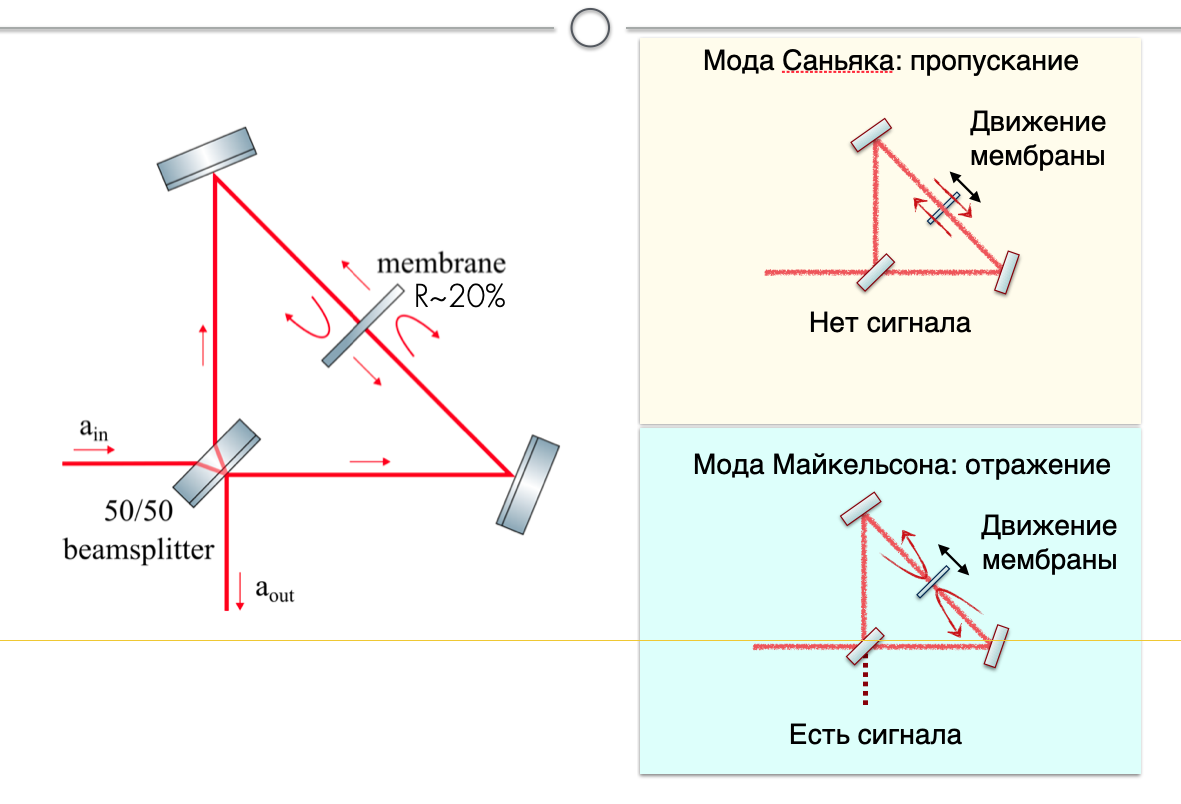
Интерферометр Майкельсона-Саньяка
Одной из главных сложностей интерферометра оказывается его настройка: свет должен идеально перекрываться на центральном делителе луча, иначе интерференции не случается, и мы теряем в чувствительности и в сжатом свете. Особенно это сложно, когда интерферометр находится внутри вакуумной камеры или криостата. Чтобы сделать интерферометр как можно более стабильным, мы сделали его из единого блока материала с низким коэффициентом температурного расширения, оптимизировав его форму так, что он не искривлялся при охлаждении. А еще он был покрыт золотым напылением, чтобы максимально изолировать его от теплового излучения извне. Этот блок мы засунули в криостат, который мог охладить его до 20К (-253С).
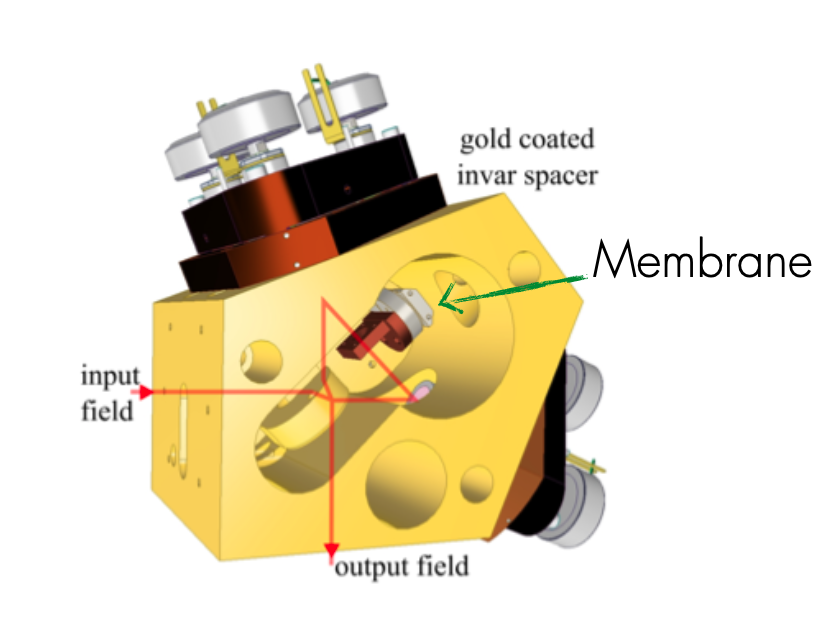
Схематическое представление интерферометра

Фотография интерферометра в разобранном виде: слева — интерферометр и пьезомоторы, смещающие зеркала при низких температурах. Справа — мембрана в держателе.
Рекомендую почитать статью на Хабре, которая является отличным введением в сжатые состояния света.
Сжатый свет можно создавать по-разному, и мы используем нелинейный кристалл.
Когда кристалл накачивают фотонами, нелинейный процесс приводит к созданию из одного фотона накачки двух фотонов с половиной энергии (частоты) фотона накачки. Эти фотоны оказываются в квантово-запутанном состоянии . Поток таких парных фотонов оказывается более упорядоченным, ��ем поток обычного света, т.к. дробовой шум оказывается снижен — эффект сжатия.
При этом неопределенность фазы будет снижена, в пределе до нуля, за счет увеличения неопределенности амплитуды. Можно сделать и наоборот, уменьшить неопределенность амплитуды. В наших экспериментах мы сжимаем не сам свет, а квантовые флуктуации нулевого состояния поля (т.е. то, что называется вакуумными флуктуациями). У такого сжатого вакуума средняя амплитуда равна нулю и есть только неопределенность фазы и амплитуды.

Принцип работы сжатого света в нелинейном кристалле. Красная линия сверху слева показывает преобразование входного света в выходной в зависимости от амплитуды. Снизу фиолетовая синусоида показывает сумму волны накачки (зеленая) и вакуумных флуктуаций основного света (красное). После нелинейного кристалла (справа) разные части этой волны получают разное усиление: одни усиливаются, другие подавляются. Шум при этом оказывается уменьшен в одни моменты времени и увеличен в другие (справа красный). Это эффект сжатия.
В эксперименте мы сначала используем нелинейный процесс для создания луча накачки, уменьшив длину волны с 1550нм до 775нм (SHG), а потом используем эту накачку для сжатия вакуумных флуктуаций на длине волны в 1550нм. Потом мы измеряем получившийся свет в интерферометре, совмещая его с лазерным лучом на делителе. Такой подход называется гомодинным детектированием.
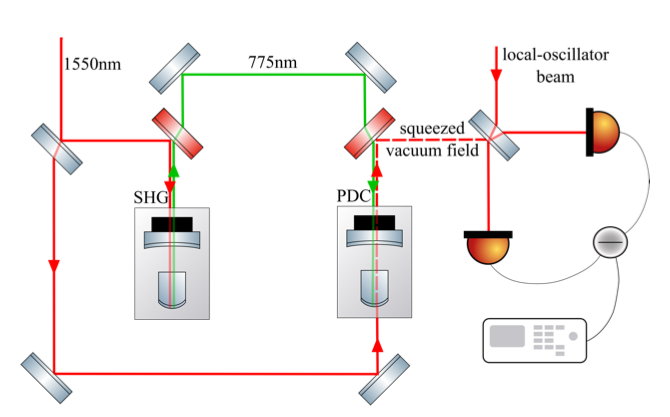
В этом эксперименте у нас было около 8.7 дБ сжатия на входе в интерферометр (снижение шума в 7.5 раз), но вообще мы умеем делать гораздо более сильное сжатие теперь — до 30 раз (15 дБ). Как я писал выше, сжатый свет очень сильно подвержен оптическим потерям, и улучшение чувствительности у нас было не таким значительным (4.8дБ).
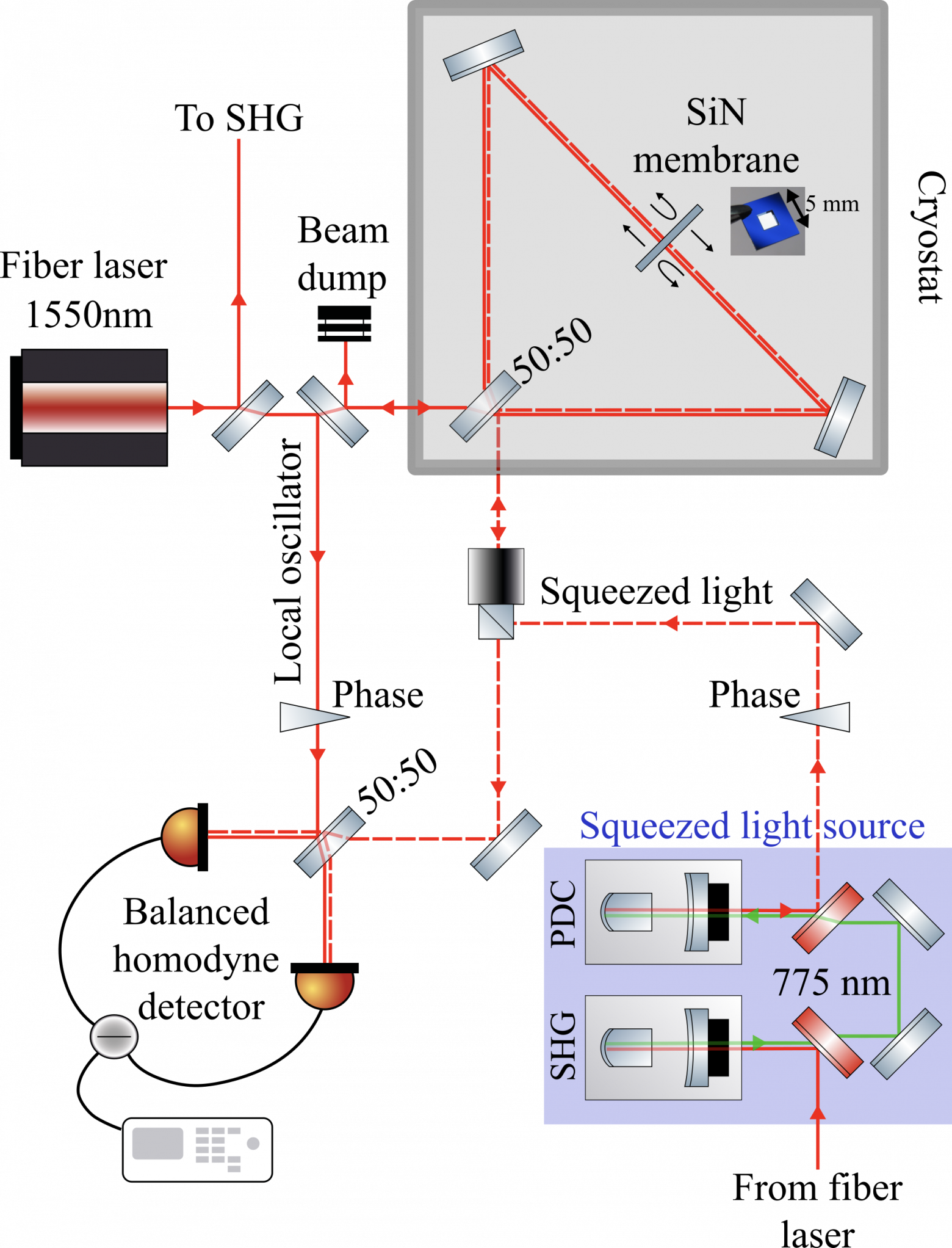
Сжатый свет мы направляем в интерферометр с сигнального порта. Он проходит через интерферометр, и выходит обратно вместе с сигналом от движения мембраны. Оба они направляются на гомодинный детектор.
Все фазы света нужно контролировать: резонаторы должны оставаться в резонансе с основным лучом, фазы сжатого света должны совпадать с фазами сигнала, интерферометр должен оставаться правильно настроенным, гомодинный детектор должен измерять правильную фазу.
В итоге все вместе это занимает большую комнату:

В результате, мы смогли наблюдать тепловое движение нашей мембраны и охладить ее до 100К и до 20К. Это охлаждение напрямую можно было наблюдать в спектре ее движения: с уменьшением температуры уменьшился и шум. С другой стороны, мы используем сжатый свет и подавляем дробовой шум в три раза. В результате, получается такой прототип гравитационно-волнового детектора, в котором мы впервые совмещаем охлажденный интерферометр с квантовым сжатием.

Самое главное, мы демонстрируем, что возможно поддерживать настройку интерферометра при охлаждении до низких температур и не вносить потерь, которые бы уменьшали степень квантовых корреляций в системе.
Основная часть работы была проделана аспиранткой в нашей лаборатории (картинки по большей части взяты из ее диссертации). До этого результата мы шли больше 6 лет, и все умещается на 4 страницах статьи. Вот так мы проводим время в лабораториях квантовой оптики. В следующий раз расскажу про другой эксперимент и покажу больше внутренностей оптики и всякий гикпорн.
Squeezed-light interferometry on a cryogenically-cooled micro-mechanical membrane

Квантовые технологии помогают нам в самых разных областях. Например, когда нам нужно измерить очень слабый сигнал, а квантовые шумы в системе очень мешают. Это традиционная проблема, например, в гравитационно-волновых детекторах, в которых квантовые ф��уктуации в амплитуде и фазе лазера, используемого для измерения положения зеркал, мешают наблюдению гравитационных волн. Я об этом рассказывал в своей статье про детектор Einstein Telescope, который появится в Европе в недалеком будущем.
У нас в эксперименте получился маленький прототип этого детектора. Наша статья об этом эксперименте была опубликована в Physical Review Letters,
а препринт тут: Squeezed-light interferometry on a cryogenically-cooled micro-mechanical membrane.
1. Краткое введение
В природе множество слабых сил, которые ученым очень хотелось бы изучить.
Проблема в том, что измерить силу напрямую мы не можем, а можем только наблюдать ее эффект на разные тела.
Самый простой и эффективный способ измерить силу — использовать маятник. Сила смещает маятник, и мы измеряем это смещение. Когда частота силы близка к резонансной частоте маятника, смещение оказывается значительно усиленным, и мы можем наблюдать хороший сигнал.
Чтобы измерять смещение маятника, удобно использовать свет. Когда мы светим лазером на маятник, покрытый отражающим веществом, фаза отраженного света содержит информацию о смещении маятника.
Фазу света напрямую мы наблюдать не можем, для этого нужен интерферометр.

Интерферометр Майкельсона: лазерный луч делится два две равных части на делителе луча (beam splitter), отражается от подвижных зеркал, где приобретает фазу с информацией об их смещении. После возвращения на делитель луча, разные фазы луча интерферируют (амплитуды складываются или вычитаются), и на выходе мы видим сигнал, пропорциональный смещению зеркал.
На этом принципе работают не только детекторы гравитационных волн, но и большая часть сенсоров.
К сожалению, кроме сигнала в таком детекторе будет еще множество разных источников шума.
Про некоторые я писал в своей статье про детектор Einstein Telescope, а здесь ограничусь только двумя.
1. Тепловой шум
Представим маятник как зеркальце, подвешенное на нитке.
Тепловое броуновское движение молекул в этой нитке приводит возбуждает колебания зеркала. Это движение в принципе случайное и может быть представлено как сила действующая на зеркало на разных частотах. На частотах близких к резонансу маятника, эта сила приводит к резонансному увеличению смещения зеркала. И хотя спектр тепловой силы белый (т.е. сила одинаковая на всех частотах), при измерении спектра движения зеркала мы увидим характерный пик на резонансной частоте.

Спектр теплового шума: смещение маятника под действием теплового шума на разных частотах. Чем меньше температура, тем меньше шум. Украдено отсюда.
Тепловой шум зависит от температуры (чем ниже, тем меньше шум) и от качества нитки (количества потерь). Строго говоря, есть флуктуационно-диссипационная теорема, которая связывает наблюдаемый шум с диссипацией в системе.
Соответственно, в будущих детекторах гравитационных волн с этим шумом будут бороться двумя путями: охлаждением подвесов (и зеркал) и увеличением их качества. В нашем эксперименте мы наблюдали спектр теплового шума и уменьшали его с помощью охлаждения, но об этом ниже.
2. Квантовый дробовой шум
свет имеет квантовую природу, отдельные фотоны летят с разной случайной задержкой. Другими словами, фаза луча света оказывается случайной.
Когда мы пытаемся измерить фазовый сигнал от внешней силы, он оказывается ограничен этой фазовой неопределенностью. На детекторе мы видим шум белого спектра, который оказывается фундаментальным ограничением в точности измерений. Все детекторы ограничены дробовым шумом. Несмотря на его фундаментальность, можно использовать квантовые корреляции, чтобы снизить уровень этого шума.
Для этого нужно вспомнить немного квантовой механики. Неопределенность в фазе и неопределенность в амплитуде лазера связаны соотношением Гейзенберга:
В обычном лазерном луче эти неопределенности равны. Однако, можно сжать неопределенность в фазе за счет увеличения неопределенности амплитуды — главное, чтобы их произведение удовлетворяло соотношению неопределенности. Такой свет называется сжатым со степенью G:
Мы воспользуемся как раз таким трюком, и сожмем неопределенность в фазе, позволив улучшить наблюдение сигнала. Кстати, гравитационно-волновые детекторы уже используют сжатый свет для всех последних наблюдений. Мы еще недавно делали эксперимент, где игрались с этим сжатым светом, и я писал об этом на Хабре.
Итак, разобравшись с основами, перейду к эксперименту.
2. Наш интерферометр
В нашем эксперименте мы использовали в качестве маятника маленькую мембрану со стороной в 1мм и толщиной в��его 50нм.


Слева: фотография мембраны (маленькое окошко в центре серой рамки). Мембрана натянута как барабан на рамку, и колеблется внутри. Справа: иллюстрация смещения мембраны.
Такая мембрана колеблется на частоте около 400кГц, и ее добротность (количество осцилляций до потери половины энергии) составляет порядка 105. Для этого, правда, приходится ее поместить в вакуум, иначе воздух давит на нее слишком сильно, и она не колеблется.
А еще она достаточно прозрачная: ее коэффициент отражения составляет всего 20%.
Это не очень удобно, потому что если использовать такую мембрану в интерферометре Майкельсона, большая часть сигнала будет потеряна. Хуже того, когда мы захотим использовать сжатый свет, эти квантовые корреляции тоже потеряются, а они особенно чувствительны к потерям. Так что мы решили использовать другую конфигурацию интерферометра, «сложив» два плеча интерферометра Майкельсона так, что два зеркала оказались одним — нашей мембраной.
В таком интерферометре есть две моды: часть света проходит сквозь мембрану, и просто выходит из интерферометра, не неся никакого сигнала (это мода Саньяка). Другая часть отражается и приобретает фазу, пропорциональную смещению мембраны, и мы получаем сигнал на выходе интерферометра.

Интерферометр Майкельсона-Саньяка
Одной из главных сложностей интерферометра оказывается его настройка: свет должен идеально перекрываться на центральном делителе луча, иначе интерференции не случается, и мы теряем в чувствительности и в сжатом свете. Особенно это сложно, когда интерферометр находится внутри вакуумной камеры или криостата. Чтобы сделать интерферометр как можно более стабильным, мы сделали его из единого блока материала с низким коэффициентом температурного расширения, оптимизировав его форму так, что он не искривлялся при охлаждении. А еще он был покрыт золотым напылением, чтобы максимально изолировать его от теплового излучения извне. Этот блок мы засунули в криостат, который мог охладить его до 20К (-253С).

Схематическое представление интерферометра

Фотография интерферометра в разобранном виде: слева — интерферометр и пьезомоторы, смещающие зеркала при низких температурах. Справа — мембрана в держателе.
3. Сжатый свет
Рекомендую почитать статью на Хабре, которая является отличным введением в сжатые состояния света.
Сжатый свет можно создавать по-разному, и мы используем нелинейный кристалл.
Когда кристалл накачивают фотонами, нелинейный процесс приводит к созданию из одного фотона накачки двух фотонов с половиной энергии (частоты) фотона накачки. Эти фотоны оказываются в квантово-запутанном состоянии . Поток таких парных фотонов оказывается более упорядоченным, ��ем поток обычного света, т.к. дробовой шум оказывается снижен — эффект сжатия.
При этом неопределенность фазы будет снижена, в пределе до нуля, за счет увеличения неопределенности амплитуды. Можно сделать и наоборот, уменьшить неопределенность амплитуды. В наших экспериментах мы сжимаем не сам свет, а квантовые флуктуации нулевого состояния поля (т.е. то, что называется вакуумными флуктуациями). У такого сжатого вакуума средняя амплитуда равна нулю и есть только неопределенность фазы и амплитуды.

Принцип работы сжатого света в нелинейном кристалле. Красная линия сверху слева показывает преобразование входного света в выходной в зависимости от амплитуды. Снизу фиолетовая синусоида показывает сумму волны накачки (зеленая) и вакуумных флуктуаций основного света (красное). После нелинейного кристалла (справа) разные части этой волны получают разное усиление: одни усиливаются, другие подавляются. Шум при этом оказывается уменьшен в одни моменты времени и увеличен в другие (справа красный). Это эффект сжатия.
В эксперименте мы сначала используем нелинейный процесс для создания луча накачки, уменьшив длину волны с 1550нм до 775нм (SHG), а потом используем эту накачку для сжатия вакуумных флуктуаций на длине волны в 1550нм. Потом мы измеряем получившийся свет в интерферометре, совмещая его с лазерным лучом на делителе. Такой подход называется гомодинным детектированием.

В этом эксперименте у нас было около 8.7 дБ сжатия на входе в интерферометр (снижение шума в 7.5 раз), но вообще мы умеем делать гораздо более сильное сжатие теперь — до 30 раз (15 дБ). Как я писал выше, сжатый свет очень сильно подвержен оптическим потерям, и улучшение чувствительности у нас было не таким значительным (4.8дБ).
Пример данных

Фаза гомодинного детектора меняется периодически так, что мы наблюдаем сжатый и анти-сжатый свет, что видно на зеленой кривой. Фиолетовая прямая — уровень дробового шума вакуумного состояния света.

Фаза гомодинного детектора меняется периодически так, что мы наблюдаем сжатый и анти-сжатый свет, что видно на зеленой кривой. Фиолетовая прямая — уровень дробового шума вакуумного состояния света.
4. Совмещаем все вместе

Сжатый свет мы направляем в интерферометр с сигнального порта. Он проходит через интерферометр, и выходит обратно вместе с сигналом от движения мембраны. Оба они направляются на гомодинный детектор.
Все фазы света нужно контролировать: резонаторы должны оставаться в резонансе с основным лучом, фазы сжатого света должны совпадать с фазами сигнала, интерферометр должен оставаться правильно настроенным, гомодинный детектор должен измерять правильную фазу.
В итоге все вместе это занимает большую комнату:

Еще картинки




В результате, мы смогли наблюдать тепловое движение нашей мембраны и охладить ее до 100К и до 20К. Это охлаждение напрямую можно было наблюдать в спектре ее движения: с уменьшением температуры уменьшился и шум. С другой стороны, мы используем сжатый свет и подавляем дробовой шум в три раза. В результате, получается такой прототип гравитационно-волнового детектора, в котором мы впервые совмещаем охлажденный интерферометр с квантовым сжатием.

Самое главное, мы демонстрируем, что возможно поддерживать настройку интерферометра при охлаждении до низких температур и не вносить потерь, которые бы уменьшали степень квантовых корреляций в системе.
Основная часть работы была проделана аспиранткой в нашей лаборатории (картинки по большей части взяты из ее диссертации). До этого результата мы шли больше 6 лет, и все умещается на 4 страницах статьи. Вот так мы проводим время в лабораториях квантовой оптики. В следующий раз расскажу про другой эксперимент и покажу больше внутренностей оптики и всякий гикпорн.
Squeezed-light interferometry on a cryogenically-cooled micro-mechanical membrane
И напоследок: если хотите понаблюдать за моими попытками разобраться в том, как вести научный твиттер на английском языке, добро пожаловать: @hbar_universe.