Все мы знаем, что если надуть пластиковую бутылку горячим воздухом, крепко-накрепко закрыть крышкой, а потом охладить, то бутылка сожмётся. Причина этого лежит в физике 8-го класса, или, если точнее, в законе Гей-Люссака, утверждающем, что отношение объёмов при разных температурах равно отношению абсолютных температур. То есть ещё со школьных времён (а может и раньше) нам всем известно, что при нагревании некоторого количества газа его объём увеличивается, а при охлаждении — уменьшается.
А что насчёт того, из чего этот газ состоит? Увеличивается ли объём самих частичек газа, то есть размер атомов и молекул? Банальный ответ на этот банальный вопрос под катом.
Ответ на этот вопрос весьма прост: как мы определимобъём размер частиц (что такое размер атома/молекулы в зависимости от температуры), такой ответ мы и получим. Поскольку атомы по-своей сути — это одноатомные молекулы, то дальше мы будем называть все эти частицы единым термином "молекула".
Если взять бутылку с газом, и из этой бутылки взять одну единственную молекулу, то окажется, что для неё не возможно (по-честному) даже принципиально измерить температуру. Частица находится в каком-то конкретном (квантовом) состоянии, которое мы можем определить и измерить, но при этом мы не сможем засунутьей в в неё термометр и узнать сколько там у неё градусов. Связанно это с тем, что «температура» — это свойство макроскопических (т.е. больших) систем, состоящих из большого числа частиц. А значит если молекул в системе мало, то и измерять у этой системы нечего. «Большое число частиц», конечно, это плавающее понятие, но обычно оно измеряется в молях, или в числах Авогадро (
), поэтому очевидно, что одна молекула горааааздо меньше этого порядка величин, а значит само понятие температуры не применимо к одной, двум, да даже десяти молекулам.
Но что вообще такое температура? Ещё со школы мы знаем, что есть т.н. абсолютная температура T, измеряемая в градусах Кельвина. Именно она стоит во всех газовых законах, в частности в уравнении Менделеева-Клайперона.
Абсолютная температура связанна с относительной температурой t, измеряемой в градусах Цельсия, как
, и абсолютный ноль (T=0, или же 
) — это недостижимая величина. Ещё всем в голову вбивают мантру:
Но эта мантра не объясняет, что же именно из себя представляет температура.
Попробуем разобраться. Начнём с простого примера. Закроем глаза и представим себе Африку: жаркую, солнечную, заполненную равнинными саваннами, и с горой Килиманджаро торчащей посередине. А ещё там есть слоны.
Каждый слон имеет определённую (большую) массу, и поэтому любое поднятие своей туши из равнинной местности в горную — это большая затрата энергии.
Представим, что слоны голодные, поэтому энергии у них мало. Будучи слоном, я бы в таком состоянии не попёрся бы в гору, а тусовался бы в саванне. В горы бы я ходил только по очень-очень большой нужде. В результате, если бы мы сняли фотографию Африки со спутника, она бы выглядела примерно так, как показано на картинке ниже: много-много слонов на равнине, и очень мало смелых и отчаянных в горах, причём, чем выше — меньше вероятность найти слона.
А теперь представим, что слоны хорошенько поели, да ещё какой-нибудь [Роскомнадзор] ещё для скорости им в еду подсыпали, так что энергии у слонов много. В этом случае, что равнина, что гора, слоны будут туда переться без особой устали, поэтому теперь вероятность отыскать слона на равнине и в горах будет отличаться уже меньше, чем в предыдущем примере (см. картинку ниже), хотя всё ещё будет сохраняться правило: чем выше на гору — тем меньше слонов.
Эти два примера весьма точно иллюстрируют случаи газа с низкой (первый) и высокой (второй) температурой. У каждой молекулы (слона) есть какая-то своя энергия, в нашем примере — это гравитационная энергия
, где m — масса, g = 9.8 м/c2 — ускорение свободного падения, а h — высота над равниной. Из энергии каждой конкретной частицы (места, где нашли слона) мы не можем ничего сказать о том, как всех слонов покормили в целом, но именно то, сколько на всех выделили еды, или другими словами, сколько энергии вкачали в среднем во всю систему, даст нам распределение слонов по ландшафту Африки. Собственно, температура в наших примерах — это общая величина накормленности всех слонов во всей Африке. Именно поэтому мантра из школьного курса физики и оказывается верна — температура — это то, сколько в среднем энергии (причем, как кинетической, так и потенциальной) имеет каждая молекула, или, что в данном случае эквивалентно, какова вероятность найти частицу с очень большой энергией. Но более точно, температура — это параметр распределения Больцмана (или Гиббса) — распределения частиц по состояниям с различной энергией. Это распределение говорит нам, что чем выше температура, тем больше высокоэнергетических молекул относительно числа низкоэнергетических мы имеем.
Теперь, собственно, можно перейти к вопросу: а растут ли, например, атомы при росте температуры. Само собой, каждый конкретный атом находится в каком-то квантовом состоянии, поэтому от температуры его размер не зависит, но вот средний размер всех атомов в сосуде с газом от той самой температуры зависеть уже будет.
Представим себе, например, атом водорода: тяжёлый протон, а вокруг него летает электрон. Поскольку протон положительный, а электрон отрицательный, то один притягивает другой по закону Кулона, который выглядит точно так же как ньютоновская гравитация, поэтому в этом смысле атом вполне себе напоминает, например, Солнце и Землю, летающую вокруг него. Только, как говорит нам (далеко не полностью удачная, см. например, тут) атомная модель Бора, в отличие от системы «звезда + планета», электрон летает вокруг ядра только по орбитам определённого радиуса.
Так или иначе, чем больше энергии мы закачиваем в атом водорода, тем более широкая орбита будет доступна электрону для полёта вокруг ядра. Естественно, если мы возьмём один конкретный атом, мы можем узнать его орбиту, и она ничего нам о температуре всех атомов не скажет. Но вот если мы измерим радиусы у множества атомов, а потом усредним полученные величины, то у нас действительно возникнет зависимость от температуры для этого среднего числа. В результате получится что-то типа такой картинки:
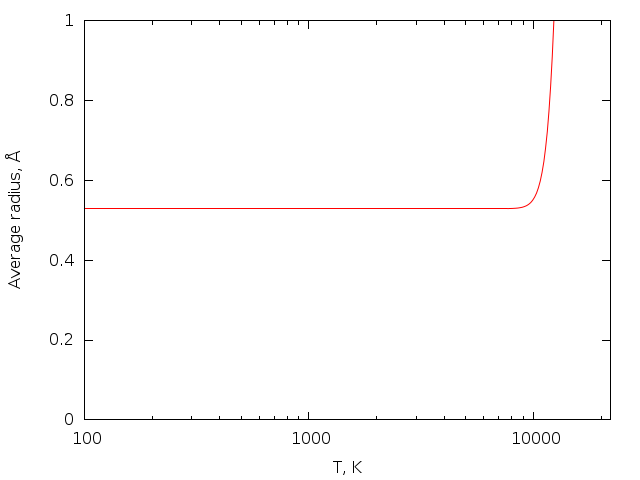
Из неё видно, что чтобы начать замечать хоть какие-то изменения в размере электронной оболочки, нужно ооочень сильно нагреть атом (в данном случае до более 10000 градусов). Это в целом общий тренд.
Иными словами, ответ на вопрос поста: да, при нагревании электронные оболочки атомов (и молекул) в среднем расширяются. Но, это увеличение очень маленькое, и требует нагрева до очень высоких температур, к которым мы в обыденной жизни не привыкли.
Теперь зададимся вопросом: а что если наша молекула составлена не из одного, а из двух, трёх или более атомов? Можем ли мы что-то сказать о межатомных расстояниях в ней, как ведут они себя при повышении температуры? Для простоты, естественно, ограничимся двухатомными молекулами, кои, в частности, составляют как минимум 98.7 % нашей атмосферы (азот и кислород).
У нас есть один атом, у нас есть второй атом: ммммм, и расстояние между ними, обозначим его как R. Как ведёт себя потенциальная энергия взаимодействия этих атомов в зависимости от R?
В итоге мы понимаем, что кривая потенциальной энергии взаимодействия имеет следующий вид:
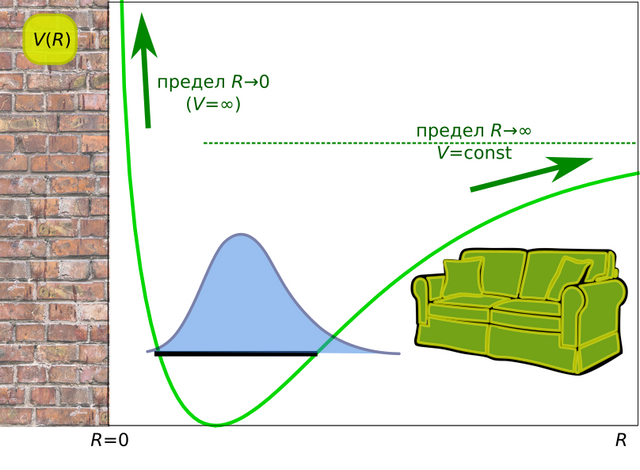
Атомы в молекуле всегда колеблются, даже при абсолютном нуле, когда никакой лишней энергии не осталось. Из-за принципа неопределённости они не могут просто скатиться в минимальную по энергии точку на потенциале исдохнуть лежать, свернувшись калачиком: им приходится совершать т.н. нулевые колебания. Если же энергия у них выше, то и колеблются они с большей амплитудой. Поэтому возникает вопрос: а как конкретно колеблются атомы?
Если бы слева и справа от точки минимума потенциал был одинаков, как, например, в случае закона Гука, то атомы во время колебаний отклонялись бы в область малых значений межатомных расстояний ровно то же количество времени, сколько и в область больших значений. В этом случае бы среднее значение межатомного расстояния при любой температуре было бы равно значению расстояния в точке минимума. Иными словами, если бы мы взяли газ, и в любой момент времени сфоткали все молекулы, а потом посчитали бы среднее значение для всех расстояний между атомами, то в итоге получили бы расстояние в точке минимума.
Но реальность у нас другая: слева от точки минимума (при R → 0) у молекулы стоит жёсткая стенка, а справа (при R → ∞) — мягкий диван. Вопрос: где будет больше времени проводить молекула: долбиться о стенку, или валяться на диване? Правильно: конечно на диване. Иными словами, распределение расстояний в молекуле, что при абсолютном нуле, что при какой-то температуре, будет несимметричным, поэтому среднее значение расстояний будет сдвинуто в сторону больших расстояний относительно минимального. Мало того, при повышении температуры, т.е. когда мы будем закачивать больше кинетической энергии в систему, увеличивая амплитуду колебаний, молекула будет видеть гораздо более жёсткую стенку, и гораздо более мягкий диван. Поэтому среднее значение межатомных расстояний будет расти с ростом температуры, а значит и средний размер молекул, причём всех, не только двухатомных, будет увеличиваться.
К сожалению, чтобы посчитать этот рост среднего расстояния, потребуется много больше усилий, чем в случае атома водорода. Но можно пойти другим путём, и поискать, а не исследовался ли этот вопрос в экспериментах?
И порывшись на просторах этих наших Интернетов, можно набрести на следующую работу: J. Chem. Phys. 79, 170 (1983). В ней делали эксперимент буквально описанный выше:
В результате они, в частности, получили следующую зависимость средней длины двойной связи C=O в молекуле углекислого газа (O=C=O):
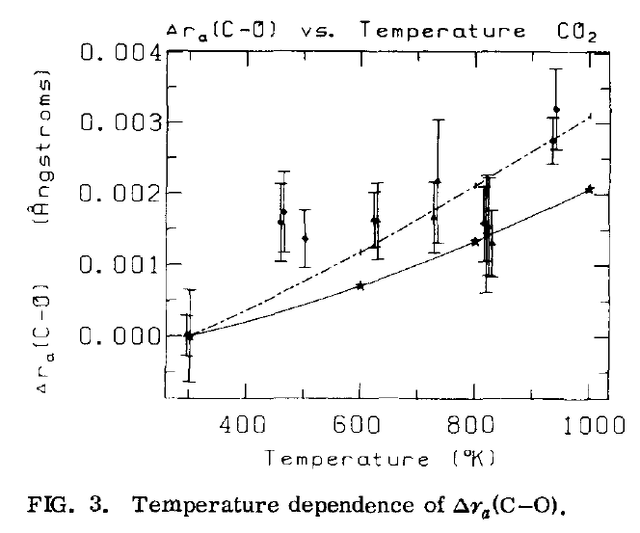
Из графика видно, что при нагреве от комнатной температуры до 1000 градусов К это среднее значение выросло почти на 0.004 Å (1 ангстрем, Å, = 10—10 метров). Конечно, в наших привычных величинах это очень мало, но сама длина связи C=O в этой молекуле составляет 1.2 Å, так что это рост на почти 0.3 %! Вполне себе заметная величина при нагреве, достижимом привычными средствами (например, газовой плитой).
Да хотя бы просто ради любопытства. Разве не прикольно поспорить с коллегой на чашку кофе, что при нагреве контейнера с едой в микроволновке помимо объёма газа увеличится и размер частиц газа? Ну и в практическом смысле это тоже важно. Все эти температурные расширения/уменьшения всяких макроскопических объектов, таких как рельсы, провода линий электропередач, да даже крышки банки под горячей водой, работают ровно по тому же механизму, что и для молекул газа: средние межатомные расстояния увеличиваются, т.к. в систему при увеличении температуры закачивается больше энергии движения частиц. И по-моему, осознание того, что за такими обыденными явлениями стоят такие нетривиальные процессы, вдохновляет на новые подвиги и свершения.
Всех благ, и да пребудет с Вами межатомная сила.
А что насчёт того, из чего этот газ состоит? Увеличивается ли объём самих частичек газа, то есть размер атомов и молекул? Банальный ответ на этот банальный вопрос под катом.
Ха-ха, попались!
Ответ на этот вопрос весьма прост: как мы определим
Если взять бутылку с газом, и из этой бутылки взять одну единственную молекулу, то окажется, что для неё не возможно (по-честному) даже принципиально измерить температуру. Частица находится в каком-то конкретном (квантовом) состоянии, которое мы можем определить и измерить, но при этом мы не сможем засунуть
), поэтому очевидно, что одна молекула горааааздо меньше этого порядка величин, а значит само понятие температуры не применимо к одной, двум, да даже десяти молекулам.Что такое температура?
Но что вообще такое температура? Ещё со школы мы знаем, что есть т.н. абсолютная температура T, измеряемая в градусах Кельвина. Именно она стоит во всех газовых законах, в частности в уравнении Менделеева-Клайперона.
Для забывших, как выглядит уравнение Менделеева-Клайперона
Это уравнение имеет вид 
, где P — давление, V — объём, n — количество вещества (в молях), R = 8.314 Дж/(моль · К) — универсальная газовая постоянная, а T — абсолютная температура в Кельвинах (К).
, где P — давление, V — объём, n — количество вещества (в молях), R = 8.314 Дж/(моль · К) — универсальная газовая постоянная, а T — абсолютная температура в Кельвинах (К).Абсолютная температура связанна с относительной температурой t, измеряемой в градусах Цельсия, как
, и абсолютный ноль (T=0, или же ) — это недостижимая величина. Ещё всем в голову вбивают мантру:абсолютная температура является мерой средней кинетической энергии молекул.
Но эта мантра не объясняет, что же именно из себя представляет температура.
Попробуем разобраться. Начнём с простого примера. Закроем глаза и представим себе Африку: жаркую, солнечную, заполненную равнинными саваннами, и с горой Килиманджаро торчащей посередине. А ещё там есть слоны.
Каждый слон имеет определённую (большую) массу, и поэтому любое поднятие своей туши из равнинной местности в горную — это большая затрата энергии.
Представим, что слоны голодные, поэтому энергии у них мало. Будучи слоном, я бы в таком состоянии не попёрся бы в гору, а тусовался бы в саванне. В горы бы я ходил только по очень-очень большой нужде. В результате, если бы мы сняли фотографию Африки со спутника, она бы выглядела примерно так, как показано на картинке ниже: много-много слонов на равнине, и очень мало смелых и отчаянных в горах, причём, чем выше — меньше вероятность найти слона.
А теперь представим, что слоны хорошенько поели, да ещё какой-нибудь [Роскомнадзор] ещё для скорости им в еду подсыпали, так что энергии у слонов много. В этом случае, что равнина, что гора, слоны будут туда переться без особой устали, поэтому теперь вероятность отыскать слона на равнине и в горах будет отличаться уже меньше, чем в предыдущем примере (см. картинку ниже), хотя всё ещё будет сохраняться правило: чем выше на гору — тем меньше слонов.
Эти два примера весьма точно иллюстрируют случаи газа с низкой (первый) и высокой (второй) температурой. У каждой молекулы (слона) есть какая-то своя энергия, в нашем примере — это гравитационная энергия
, где m — масса, g = 9.8 м/c2 — ускорение свободного падения, а h — высота над равниной. Из энергии каждой конкретной частицы (места, где нашли слона) мы не можем ничего сказать о том, как всех слонов покормили в целом, но именно то, сколько на всех выделили еды, или другими словами, сколько энергии вкачали в среднем во всю систему, даст нам распределение слонов по ландшафту Африки. Собственно, температура в наших примерах — это общая величина накормленности всех слонов во всей Африке. Именно поэтому мантра из школьного курса физики и оказывается верна — температура — это то, сколько в среднем энергии (причем, как кинетической, так и потенциальной) имеет каждая молекула, или, что в данном случае эквивалентно, какова вероятность найти частицу с очень большой энергией. Но более точно, температура — это параметр распределения Больцмана (или Гиббса) — распределения частиц по состояниям с различной энергией. Это распределение говорит нам, что чем выше температура, тем больше высокоэнергетических молекул относительно числа низкоэнергетических мы имеем.
Распределение Больцмана
Собственно, распределение Больцмана имеет вид:
где n(E) — это число частиц с энергией E, R — универсальная газовая постоянная (см. предыдущий спойлер), а T, само собой, температура.
В примере же со слонами мы иллюстрировали т.н. барометрическую формулу: частный случай распределения Больцмана, показывающий как меняется давление газа с увеличением высоты:
где P(h) — это давление на высоте h,
, а M — это молярная масса газа.
где n(E) — это число частиц с энергией E, R — универсальная газовая постоянная (см. предыдущий спойлер), а T, само собой, температура.
В примере же со слонами мы иллюстрировали т.н. барометрическую формулу: частный случай распределения Больцмана, показывающий как меняется давление газа с увеличением высоты:
где P(h) — это давление на высоте h,
, а M — это молярная масса газа.Растут ли атомы от температуры?
Теперь, собственно, можно перейти к вопросу: а растут ли, например, атомы при росте температуры. Само собой, каждый конкретный атом находится в каком-то квантовом состоянии, поэтому от температуры его размер не зависит, но вот средний размер всех атомов в сосуде с газом от той самой температуры зависеть уже будет.
Представим себе, например, атом водорода: тяжёлый протон, а вокруг него летает электрон. Поскольку протон положительный, а электрон отрицательный, то один притягивает другой по закону Кулона, который выглядит точно так же как ньютоновская гравитация, поэтому в этом смысле атом вполне себе напоминает, например, Солнце и Землю, летающую вокруг него. Только, как говорит нам (далеко не полностью удачная, см. например, тут) атомная модель Бора, в отличие от системы «звезда + планета», электрон летает вокруг ядра только по орбитам определённого радиуса.
Так или иначе, чем больше энергии мы закачиваем в атом водорода, тем более широкая орбита будет доступна электрону для полёта вокруг ядра. Естественно, если мы возьмём один конкретный атом, мы можем узнать его орбиту, и она ничего нам о температуре всех атомов не скажет. Но вот если мы измерим радиусы у множества атомов, а потом усредним полученные величины, то у нас действительно возникнет зависимость от температуры для этого среднего числа. В результате получится что-то типа такой картинки:
Из неё видно, что чтобы начать замечать хоть какие-то изменения в размере электронной оболочки, нужно ооочень сильно нагреть атом (в данном случае до более 10000 градусов). Это в целом общий тренд.
Как была посчитана эта зависимость
Подробнее о формулах можно узнать в этом посте.
Если кратко, то радиус орбиты (R) в зависимости от главного квантового числа n=1,2,3… — это
где R0=5.3×10−11 метра − это боровский радиус. Энергия (E) же орбиты имеет вид
где Eh= 4.3597447222071(85)×10−18 Джоулей − это энергия Хартри.
Далее используя распределение Больцмана для одной частицы, мы можем посчитать среднее значение радиуса от температуры как
Знаменатель у нас появляется из-за того, что полная вероятность всех исходов измерений должна быть равна единице.
Если кратко, то радиус орбиты (R) в зависимости от главного квантового числа n=1,2,3… — это
где R0=5.3×10−11 метра − это боровский радиус. Энергия (E) же орбиты имеет вид
где Eh= 4.3597447222071(85)×10−18 Джоулей − это энергия Хартри.
Далее используя распределение Больцмана для одной частицы, мы можем посчитать среднее значение радиуса от температуры как
Знаменатель у нас появляется из-за того, что полная вероятность всех исходов измерений должна быть равна единице.
Иными словами, ответ на вопрос поста: да, при нагревании электронные оболочки атомов (и молекул) в среднем расширяются. Но, это увеличение очень маленькое, и требует нагрева до очень высоких температур, к которым мы в обыденной жизни не привыкли.
Растут ли молекулы от температуры?
Теперь зададимся вопросом: а что если наша молекула составлена не из одного, а из двух, трёх или более атомов? Можем ли мы что-то сказать о межатомных расстояниях в ней, как ведут они себя при повышении температуры? Для простоты, естественно, ограничимся двухатомными молекулами, кои, в частности, составляют как минимум 98.7 % нашей атмосферы (азот и кислород).
У нас есть один атом, у нас есть второй атом: ммммм, и расстояние между ними, обозначим его как R. Как ведёт себя потенциальная энергия взаимодействия этих атомов в зависимости от R?
- Если мы разведём атомы оооочень далеко друг от др��га, то химическая связь между ними давно будет разорвана. Поэтому особой разницы от того, что расстояние мы увеличим от «очень много» до «очень много и ещё чуть-чуть», мы не заметим. Иными словами при R → ∞ у нас должна быть горизонтальная асимптота.
- Если же, наоборот, мы будем пытаться впихнуть один атом в другой (R → 0), то в какой-то момент мы выгоним из пространства между этими атомами все электроны, ибо те не идиоты, чтобы тусоваться в токсичной высокоэнергетической атмосфере, и у нас останутся два голых положительно заряженных ядра, отталкивающиеся друг от друга через Кулоновскую силу. Т.е. при R → 0 у нас будет вертикальная асимптота, стремящая потенциальную энергию взаимодействия атомов в высокоэнергетическую бесконечность.
- Ну и, логично, что не будь какого-то минимума на этой потенциальной кривой между R=0 и R → ∞, то самих молекул о которых мы говорим, не существовало бы.
В итоге мы понимаем, что кривая потенциальной энергии взаимодействия имеет следующий вид:
Атомы в молекуле всегда колеблются, даже при абсолютном нуле, когда никакой лишней энергии не осталось. Из-за принципа неопределённости они не могут просто скатиться в минимальную по энергии точку на потенциале и
Если бы слева и справа от точки минимума потенциал был одинаков, как, например, в случае закона Гука, то атомы во время колебаний отклонялись бы в область малых значений межатомных расстояний ровно то же количество времени, сколько и в область больших значений. В этом случае бы среднее значение межатомного расстояния при любой температуре было бы равно значению расстояния в точке минимума. Иными словами, если бы мы взяли газ, и в любой момент времени сфоткали все молекулы, а потом посчитали бы среднее значение для всех расстояний между атомами, то в итоге получили бы расстояние в точке минимума.
Но реальность у нас другая: слева от точки минимума (при R → 0) у молекулы стоит жёсткая стенка, а справа (при R → ∞) — мягкий диван. Вопрос: где будет больше времени проводить молекула: долбиться о стенку, или валяться на диване? Правильно: конечно на диване. Иными словами, распределение расстояний в молекуле, что при абсолютном нуле, что при какой-то температуре, будет несимметричным, поэтому среднее значение расстояний будет сдвинуто в сторону больших расстояний относительно минимального. Мало того, при повышении температуры, т.е. когда мы будем закачивать больше кинетической энергии в систему, увеличивая амплитуду колебаний, молекула будет видеть гораздо более жёсткую стенку, и гораздо более мягкий диван. Поэтому среднее значение межатомных расстояний будет расти с ростом температуры, а значит и средний размер молекул, причём всех, не только двухатомных, будет увеличиваться.
К сожалению, чтобы посчитать этот рост среднего расстояния, потребуется много больше усилий, чем в случае атома водорода. Но можно пойти другим путём, и поискать, а не исследовался ли этот вопрос в экспериментах?
И порывшись на просторах этих наших Интернетов, можно набрести на следующую работу: J. Chem. Phys. 79, 170 (1983). В ней делали эксперимент буквально описанный выше:
- брали кучу молекул углекислого газа (CO2) и нагревали их до разных температур, в диапазоне температур от комнатной (300 K ≈ 25oC) до «ай как горячо» (1000 К ≈ 730oC ),
- при каждой выбранной температуре делали «фотку» всех молекул при помощи электронов (этот метод зовётся газовой электронографией, о нём можно немного почитать здесь),
- ну а дальше буквально измеряли средние значения для межатомных расстояний на каждой фотке.
В результате они, в частности, получили следующую зависимость средней длины двойной связи C=O в молекуле углекислого газа (O=C=O):
Из графика видно, что при нагреве от комнатной температуры до 1000 градусов К это среднее значение выросло почти на 0.004 Å (1 ангстрем, Å, = 10—10 метров). Конечно, в наших привычных величинах это очень мало, но сама длина связи C=O в этой молекуле составляет 1.2 Å, так что это рост на почти 0.3 %! Вполне себе заметная величина при нагреве, достижимом привычными средствами (например, газовой плитой).
��ачем это вообще знать?
Да хотя бы просто ради любопытства. Разве не прикольно поспорить с коллегой на чашку кофе, что при нагреве контейнера с едой в микроволновке помимо объёма газа увеличится и размер частиц газа? Ну и в практическом смысле это тоже важно. Все эти температурные расширения/уменьшения всяких макроскопических объектов, таких как рельсы, провода линий электропередач, да даже крышки банки под горячей водой, работают ровно по тому же механизму, что и для молекул газа: средние межатомные расстояния увеличиваются, т.к. в систему при увеличении температуры закачивается больше энергии движения частиц. И по-моему, осознание того, что за такими обыденными явлениями стоят такие нетривиальные процессы, вдохновляет на новые подвиги и свершения.
Всех благ, и да пребудет с Вами межатомная сила.
