Генетический алгоритм vs алгоритм роя частиц

Введение

К задачам поиска лучшего варианта решения (объекта, параметров или других данных) сводятся многие из проблем математики, экономики, статистики и т.д. Эти проблемы возникают, когда приходится строить математическую модель ситуации. При обработке полученной математической модели не всегда является возможным перебрать все данные, предоставленные системой, поэтому возникает потребность в разработке таких алгоритмов, которые могли бы искать оптимальные данные с некоторыми погрешностями, чтобы ограничить зону обработки данных для поиска последующих лучших значений.

В данной статье под задачей оптимизации понимается нахождение экстремума (минимума) некоторой вещественной функции в заданной области. Будут рассмотрены два самых важных алгоритма в оптимизации: генетический алгоритм и алгоритм роя частиц.

Генетический алгоритм

Краткое описание

Первым алгоритмом оптимизации будет генетический алгоритм, который, в свою очередь, является одним из эволюционных алгоритмов, то есть в его основе лежат процессы отбора, мутации и комбинирования (скрещивания). Поскольку мы оптимизируем задачу поиска глобального экстремума функции, то стоит более подробно рассмотреть каждый шаг генетического алгоритма:

Каждая особь популяции будет обладать тремя основными параметрами: положением по оси Х, положением по оси У и значением целевой функции (именно это значение будет выступать в роли основного параметра при селекции).

На первом этапе происходит создание начальной популяции, где каждая особь случайным образом получает свои координаты по Х и У. Эта популяция может быть далека от идеала, но в процессе эволюции алгоритм должен будет исправить это.

Далее идет процесс размножения. Случайным образом выбирается пара родителей, которые производят потомков. Потомки должны наследовать черты родителей. Для того, чтобы не произошло доминирования со стороны одной особи, в размножении участвуют гены обоих родителей.

После размножения отбирается часть особей, которая подвергается случайным мутациям в генах. В случае с поиском экстремума будет меняться положение индивида по координатам Х и У.

В самом конце должен произойти отбор наиболее приспособленных особей. Особи с наименьшим показателем значения целевой функции проходят дальше. Для того, чтобы популяция не росла беспрерывно, её численность регулируется определенным заданным параметром.

Шаги “размножение”, “мутация” и “отбор” повторяются до тех пор, пока не будет достигнута точка Останова. В качестве конца алгоритма зачастую выбирают либо достижение максимального числа итераций алгоритма, либо ….

Иногда добавляют новые правила для изменения популяции, например, добавляют оператор инверсии (в случае с бинарными генами) или ограничивают время жизни каждой особи. Также добавляют условия на поиск пары для скрещивания, где оба родителя будут схожи по каким-либо признакам или наоборот, будут сильно отличаться.

Реализация

Для начала необходимо реализовать класс одной особи, в качестве параметров он будет принимать: пределы области поиска экстремума, количество шагов для мутации и целевую функцию, а также у индивида будет 2 поля, отвечающих за позицию по Х и У координатам, и поле, отвечающее за значение функции в текущей позиции:

class Individ():
    """ Класс одного индивида в популяции"""
    def __init__(self, start, end, mutationSteps, function):
        # пределы поиска минимума
        self.start = start
        self.end = end
        # позиция индивида по Х (первый раз определяется случайно)
        self.x = rnd.triangular(self.start, self.end)
        # позиция индивида по Y (первый раз определяется случайно)
        self.y = rnd.triangular(self.start, self.end)
        # значение функции, которую реализует индивид
        self.score = 0
        # передаем функцию для оптимизации
        self.function = function
        # количество шагов мутации
        self.mutationSteps = mutationSteps
        # считаем сразу значение функции
        self.calculateFunction()

Теперь реализуем функцию мутации в классе самой особи:

def mutate(self):
  """ Функция для мутации индивида"""
  # задаем отклонение по Х
  delta = 0
  for i in range(1, self.mutationSteps+1):
      if rnd.random() < 1 / self.mutationSteps:
          delta += 1 / (2 ** i)
  if rnd.randint(0, 1):
      delta = self.end * delta
  else:
      delta = self.start * delta
  self.x += delta
  # ограничим наших индивидом по Х
  if self.x < 0:
      self.x = max(self.x, self.start)
  else:
      self.x = min(self.x, self.end)
  # отклонение по У
  delta = 0
  for i in range(1, self.mutationSteps+1):
      if rnd.random() < 1 / self.mutationSteps:
          delta += 1 / (2 ** i)
  if rnd.randint(0, 1):
      delta = self.end * delta
  else:
      delta = self.start * delta
  self.y += delta
  # ограничим наших индивидом по У
  if self.y < 0:
      self.y = max(self.y, self.start)
  else:
      self.y = min(self.y, self.end)

Теперь реализуем сам класс для исполнения алгоритма. В качестве параметров в класс будем передавать: размер популяции; процент популяции, который сможет воспроизводить потомство; количество шагов для мутации; шанс мутации особи; количество исполнений алгоритма (количество раз для появления нового потомства), целевую функцию, а также область поиска экстремума. Также в классе будут храниться: наилучшее значение целевой функции для всех итераций и точка (х, у),в которой было получено наилучшее значение:

class Genetic:
    """ Класс, отвечающий за реализацию генетического алгоритма"""
    def __init__(self,
                 numberOfIndividums,
                 crossoverRate,
                 mutationSteps,
                 chanceMutations,
                 numberLives,
                 function,
                 start,
                 end):
        # размер популяции
        self.numberOfIndividums = numberOfIndividums
        # какая часть популяции должна производить потомство (в % соотношении)
        self.crossoverRate = crossoverRate
        # количество шагов мутации
        self.mutationSteps = mutationSteps
        # шанс мутации особи
        self.chanceMutations = chanceMutations
        # сколько раз будет появляться новое поколение (сколько раз будет выполняться алгоритм)
        self.numberLives = numberLives
        # функция для поиска минимума
        self.function = function

        # самое минимальное значение, которое было в нашей популяции
        self.bestScore = float('inf')
        # точка Х, У, где нашли минимальное значение
        self.xy = [float('inf'), float('inf')]
        # область поиска
        self.start = start
        self.end = end

Реализуем функцию кроссовера (скрещивания). Новые координаты по Х будут находиться случайным образом между координатами первого родителя и второго родителя по Х, аналогичным образом определяются координаты потомка по У:

def crossover(self, parent1:Individ, parent2:Individ):
  """ Функция для скрещивания двух родителей

  :return: 2 потомка, полученных путем скрещивания
  """
  # создаем 2х новых детей
  child1 = Individ(self.start, self.end, self.mutationSteps, self.function)
  child2 = Individ(self.start, self.end, self.mutationSteps, self.function)
  # создаем новые координаты для детей
  alpha = rnd.uniform(0.01, 1)
  child1.x = parent1.x + alpha * (parent2.x - parent1.x)

  alpha = rnd.uniform(0.01, 1)
  child1.y = parent1.y + alpha * (parent2.y - parent1.y)

  alpha = rnd.uniform(0.01, 1)
  child2.x = parent1.x + alpha * (parent1.x - parent2.x)

  alpha = rnd.uniform(0.01, 1)
  child2.y = parent1.y + alpha * (parent1.y - parent2.y)
  return child1, child2

Теперь можно приступать к написанию функции запуска самого генетического алгоритма (назовем её startGenetic в классе Genetic). Сначала необходимо создать стартовую популяцию нашей колонии:

# создаем стартовую популяцию
pack = [self.start, self.end, self.mutationSteps,self.function]
population = [Individ(*pack) for _ in range(self.numberOfIndividums)]

В качестве конца алгоритма будем считать количество итераций, которые пережила колония. В каждой новой итерации сортируем популяцию в порядке убывания (для нахождения минимума функции) и выбираем ту часть популяции, которая будет принимать участие в размножении:

# запускаем алгоритм
for _ in range(self.numberLives):
  # сортируем популяцию по значению score
  population = sorted(population, key=lambda item: item.scor
  # берем ту часть лучших индивидов, которых будем скрещивать между собой
  bestPopulation = population[:int(self.numberOfIndividums*self.crossoverRate)]

И для каждой особи находим случайную пару, с которой она сможет дать потомство:

# теперь проводим скрещивание столько раз, сколько было задано по коэффициенту кроссовера
childs = []
for individ1 in bestPopulation:
    # находим случайную пару для каждого индивида и скрещиваем
    individ2 = rnd.choice(bestPopulation)
    while individ1 == individ2:
        individ2 = rnd.choice(bestPopulation)
    child1, child2 = self.crossover(individ1, individ2)
    childs.append(child1)
    # добавляем всех новых потомков в нашу популяцию
    population.extend(childs)            childs.append(child2)

Проводим мутации над каждой особью и отбираем наиболее приспособленных особей в новой популяции, содержащей детей:

 for individ in population:
      # проводим мутации для каждого индивида
      individ.mutate()
      # пересчитываем значение функции для каждого индивида
      individ.calculateFunction()
  # отбираем лучших индивидов
  population = sorted(population, key=lambda item: item.score)
  population = population[:self.numberOfIndividums]

И в конце каждой итерации проверяем лучшую особь в новой популяции на наилучшее значение целевой функции в течение всего времени:

# теперь проверим значение функции лучшего индивида на наилучшее значение экстремума
if population[0].score < self.bestScore:
  self.bestScore = population[0].score
  self.xy = [population[0].x, population[0].y]

На этом весь алгоритм можно считать завершенным. Запустим и проверим алгоритм на функции сферы (её минимум находится в точке 0,0):

def Sphere(x, y):
    return x**2 + y**2

a = Genetic(numberOfIndividums=500, crossoverRate=0.5, mutationSteps=15, chanceMutations=0.4,
            numberLives=200, function=Sphere, start=-5, end=5)
a.startGenetic()
print("НАЙДЕННОЕ ЗНАЧЕНИЕ:", a.xy, a.bestScore)
>>> НАЙДЕННОЕ ЗНАЧЕНИЕ: [9.900341358415679e-05, -6.0054371129849215e-05] 1.3408203393117267e-08

Как видно, алгоритм смог найти минимум функции с точностью до 5 знаков после запятой, что является очень хорошим результатом.

Алгоритм роя частиц

Немного об алгоритме

Основная идея алгоритма роя частиц заключается в коллективном поведении некоторых агентов, которые могут взаимодействовать друг с другом и с окружающей средой для решения определенной задачи. Благодаря взаимодействию частиц получается успешно решать задачи.

При решении задачи нахождения экстремума функции каждая частица характеризуется тремя параметрами: координатами в пространстве и значением целевой функции. При этом на каждом шаге частицы помнят точку, где значение целевой функции было наилучшим, и пытаются туда вернуться. Каждая частица знает координаты лучшей точки, в которой была любая другая частица. Также на перемещение каждой влияет случайное отклонение и скорость.

В классической реализации алгоритма роя частиц для определения скорости частицы используется формула:

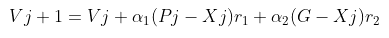
где Vj+1 - определяемая скорость частицы для новой итерации, Vj - текущая скорость частицы, Pj - координаты лучшей точки, в которой была сама частица, Xj - положение частицы на j-ой итерации, G - координаты лучшей точки, найденной всеми частицы, r1 и r2 - случайные величины в интервале от [0,1), a1 - коэффициент, определяющий значимость своего лучшего решения, a2 - коэффициент, определяющий значимость лучшего решения роя.

Однако для улучшения алгоритма можно использовать другие формулы, например

В таком решении Lj - это лучшее значение, которое было найдено среди соседних частиц. Таким образом получаем, что перемещение частицы в пространстве задается формулой:

Реализация алгоритма

Первым делом реализуем класс роя, который на вход будет принимать размер роя, коэффициенты приоритетов смещения частиц к разным точкам, количество итераций алгоритма, целевую функцию и область поиска экстремума:

class Swarm:

    def __init__(self, sizeSwarm,
                 currentVelocityRatio,
                 localVelocityRatio,
                 globalVelocityRatio,
                 numbersOfLife,
                 function,
                 start,
                 end):
        # размер популяции частиц
        self.sizeSwarm = sizeSwarm
        # коэффициенты изменения скорости
        self.currentVelocityRatio = currentVelocityRatio
        self.localVelocityRatio = localVelocityRatio
        self.globalVelocityRatio = globalVelocityRatio
        # количество итераций алгоритма
        self.numbersOfLife = numbersOfLife
        # функция для поиска экстремума
        self.function = function
        # область поиска
        self.start = start
        self.end = end
        # рой частиц
        self.swarm = []
        # данные о лучшей позиции
        self.globalBestPos = []
        self.globalBestScore = float('inf')
        # создаем рой
        self.createSwarm()

Также для реализации необходимо создать класс для одной частицы:

class Unit:

    def __init__(self, start, end, currentVelocityRatio, localVelocityRatio, globalVelocityRatio, function):
        # область поиска
        self.start = start
        self.end = end
        # коэффициенты для изменения скорости
        self.currentVelocityRatio = currentVelocityRatio
        self.localVelocityRatio = localVelocityRatio
        self.globalVelocityRatio = globalVelocityRatio
        # функция
        self.function = function
        # лучшая локальная позиция
        self.localBestPos = self.getFirsPos()
        self.localBestScore = self.function(*self.localBestPos)
        # текущая позиция
        self.currentPos = self.localBestPos[:]
        self.score = self.function(*self.localBestPos)
        # значение глобальной позиции
        self.globalBestPos = []
        # скорость
        self.velocity = self.getFirstVelocity()
        
   def getFirstVelocity(self):
        """ Метод для задания первоначальной скорости"""
        minval = -(self.end - self.start)
        maxval = self.end - self.start
        return [rnd.uniform(minval, maxval), rnd.uniform(minval, maxval)]

    def getFirsPos(self):
        """ Метод для получения начальной позиции"""
        return [rnd.uniform(self.start, self.end), rnd.uniform(self.start, self.end)]

Реализуем логику для расчета новой позиции частицы:

 def nextIteration(self):
        """ Метод для нахождения новой позиции частицы"""
        # случайные данные для изменения скорости
        rndCurrentBestPosition = [rnd.random(), rnd.random()]
        rndGlobalBestPosition = [rnd.random(), rnd.random()]
        # делаем перерасчет скорости частицы исходя из всех введенных параметров
        velocityRatio = self.localVelocityRatio + self.globalVelocityRatio
        commonVelocityRatio = 2 * self.currentVelocityRatio / abs(2-velocityRatio-sqrt(velocityRatio ** 2 - 4 * velocityRatio))
        multLocal = list(map(lambda x: x*commonVelocityRatio * self.localVelocityRatio, rndCurrentBestPosition))
        betweenLocalAndCurPos = [self.localBestPos[0] - self.currentPos[0], self.localBestPos[1] - self.currentPos[1]]
        betweenGlobalAndCurPos = [self.globalBestPos[0] - self.currentPos[0], self.globalBestPos[1] - self.currentPos[1]]
        multGlobal = list(map(lambda x: x*commonVelocityRatio * self.globalVelocityRatio, rndGlobalBestPosition))
        newVelocity1 = list(map(lambda coord: coord * commonVelocityRatio, self.velocity))
        newVelocity2 = [coord1 * coord2 for coord1, coord2 in zip(multLocal, betweenLocalAndCurPos)]
        newVelocity3 = [coord1 * coord2 for coord1, coord2 in zip(multGlobal, betweenGlobalAndCurPos)]
        self.velocity = [coord1 + coord2 + coord3 for coord1, coord2, coord3 in zip(newVelocity1, newVelocity2, newVelocity3)]
        # передвигаем частицу и смотрим, какое значение целевой фунции получается
        self.currentPos = [coord1 + coord2 for coord1, coord2 in zip(self.currentPos, self.velocity)]
        newScore = self.function(*self.currentPos)
        if newScore < self.localBestScore:
            self.localBestPos = self.currentPos[:]
            self.localBestScore = newScore
        return newScore

Теперь создадим метод для реализации алгоритма в классе Swarm и протестируем:

def startSwarm(self):
  """ Метод для запуска алгоритма"""
  for _ in range(self.numbersOfLife):
      for unit in self.swarm:
          unit.globalBestPos = self.globalBestPos
          score = unit.nextIteration()
          if score < self.globalBestScore:
              self.globalBestScore = score
              self.globalBestPos = unit.localBestPos

a = Swarm2(650, 0.1, 1, 5, 200, Sphere, -5, 5)
a.startSwarm()
print("РЕЗУЛЬТАТ:", a.globalBestScore, "В ТОЧКЕ:",a.globalBestPos)
>>> РЕЗУЛЬТАТ: 1.312199609838886e-14 В ТОЧКЕ: [1.0339745628764867e-07, -4.930478812075602e-08]
Алгоритм успешно справился с задачей.

Сравниваем алгоритмы

В википедии есть несколько функций, которые чаще всего используют для проверки алгоритмов оптимизации. Наиболее интересными, на мой взгляд, являются функции Химмельблау и Табличная функция Хольдера, так как они имеют несколько глобальных минимумов. Для того, чтобы посмотреть, как работает алгоритм, можно создать GIF при помощи библиотек matplotlib (для отрисовки графиков) и imageio (для создания GIF). Создадим обе функции:

def Himmelblau(x, y):
    return (x**2+y-11)**2 + (x+y**2-7)**2

def Holder(x, y):
    return -1 * abs(sin(x)*cos(y)*exp(abs(1 - (sqrt(x**2 + y**2))/pi) ))

Запустим по 2 раза каждый алгоритм с целевой функцией Хольдера. Первым проверим, как работает генетический алгоритм:

>>> ОПТИМИЗИРОВАННОЕ ЗНАЧЕНИЕ ФУНКЦИИ: [8.055192789475683, 9.664625935217138] -19.20850227077434
>>> ОПТИМИЗИРОВАННОЕ ЗНАЧЕНИЕ ФУНКЦИИ: [8.054968749727495, -9.664450802831455] -19.208502341200372

Посмотрим, как сходится алгоритм (для первого теста):

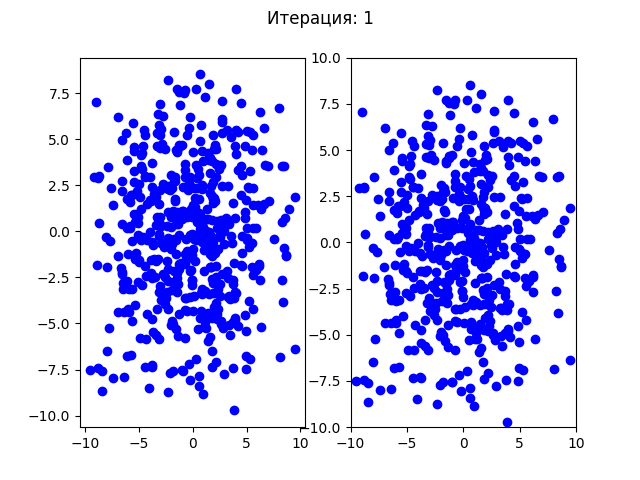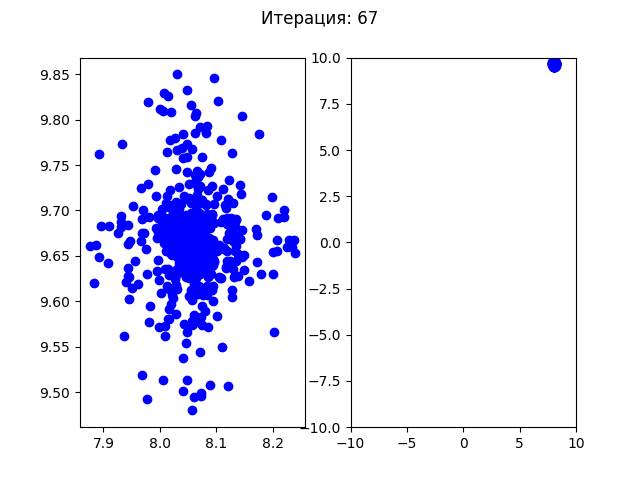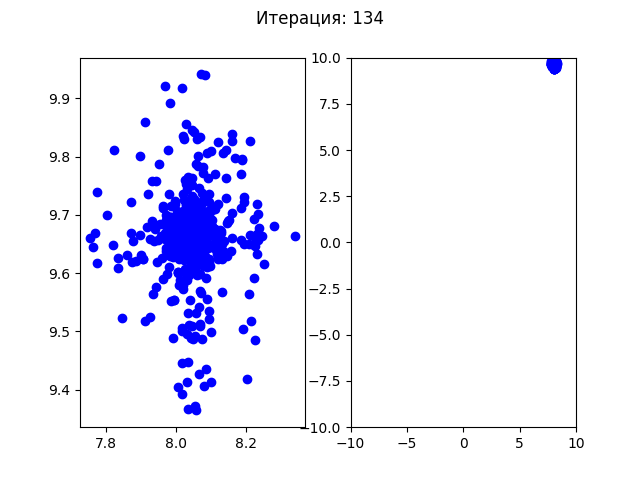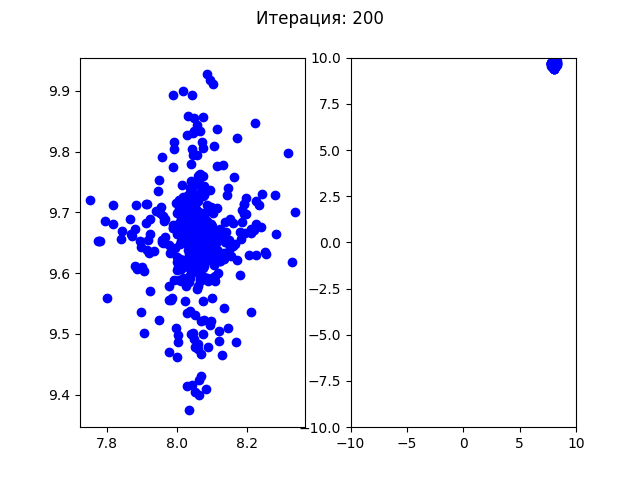
Для второго теста:

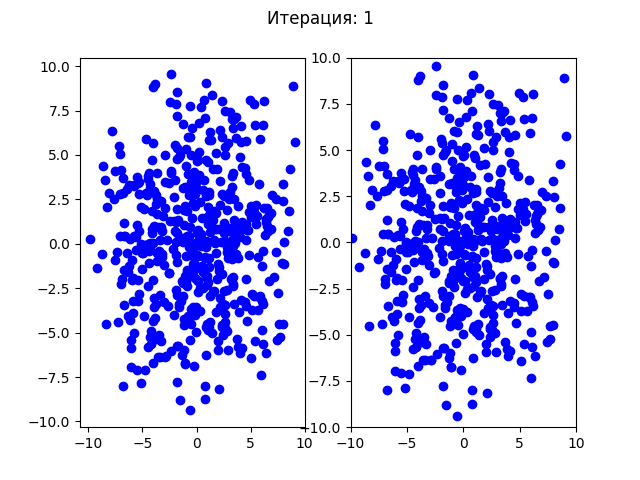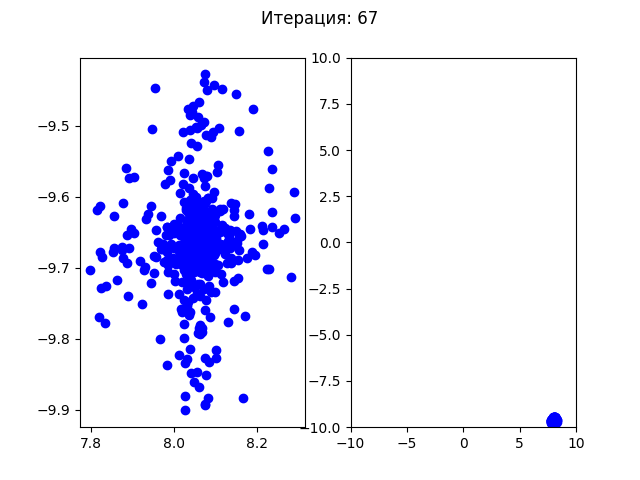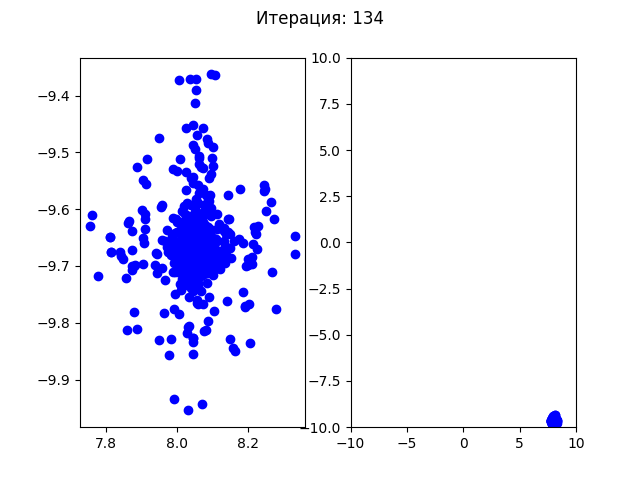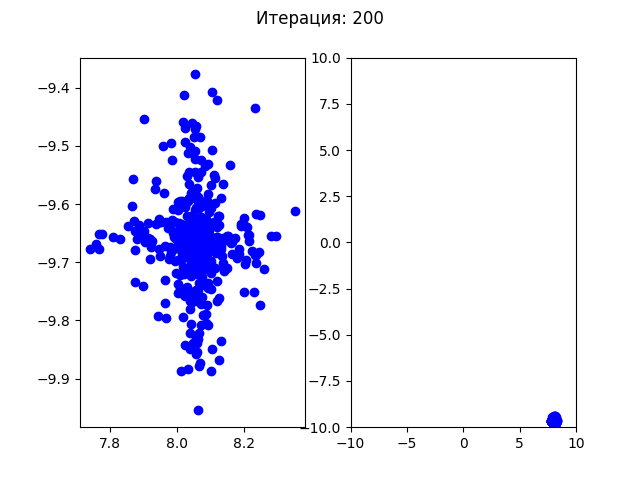
До первых 30 итераций все особи распределялись по первым найденным точкам минимума, но после этого все собираются в одной точке. Так как этот алгоритм подразумевает случайные изменения, то при каждом новом запуске программы в одной из 4х точек минимума может начать доминировать один ген и все будущие поколения будут сходиться в этой одной точке.

Давайте посмотрим, как сработает алгоритм роя частиц:

>>> РЕЗУЛЬТАТ: -19.179380799107413 В ТОЧКЕ: [-8.04199083826373, -9.612324708539033]
>>> РЕЗУЛЬТАТ: -19.20850255479626 В ТОЧКЕ: [8.055014133170205, -9.664555295609443]

Посмотрим на сходимость роя частиц для теста №1:

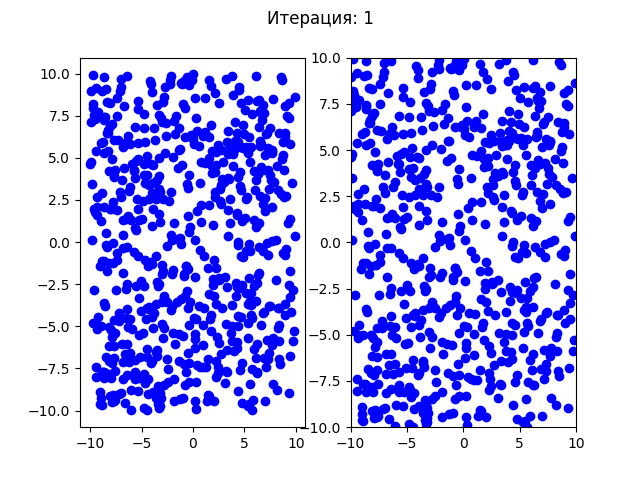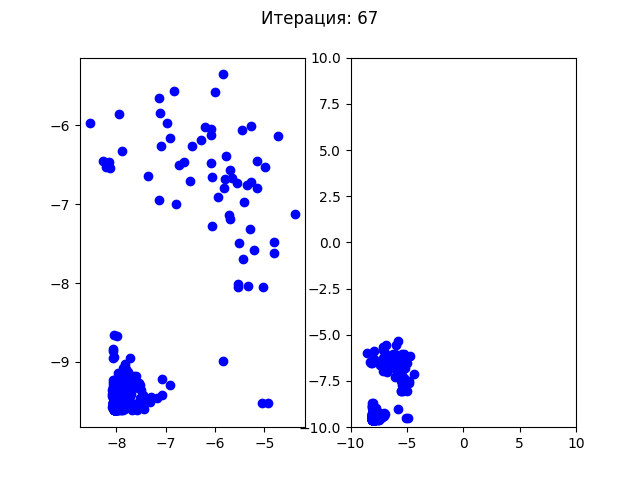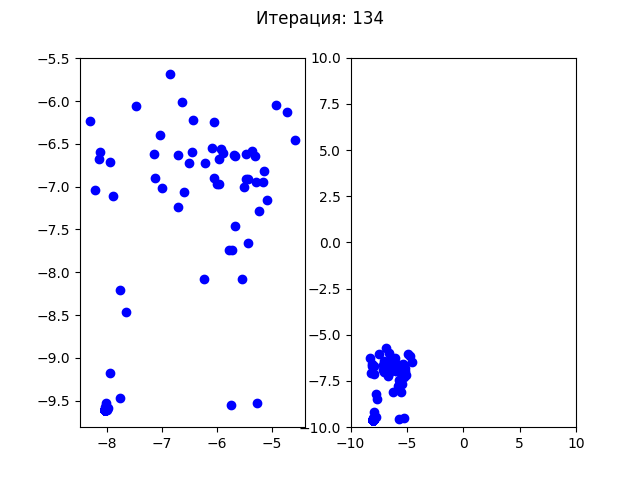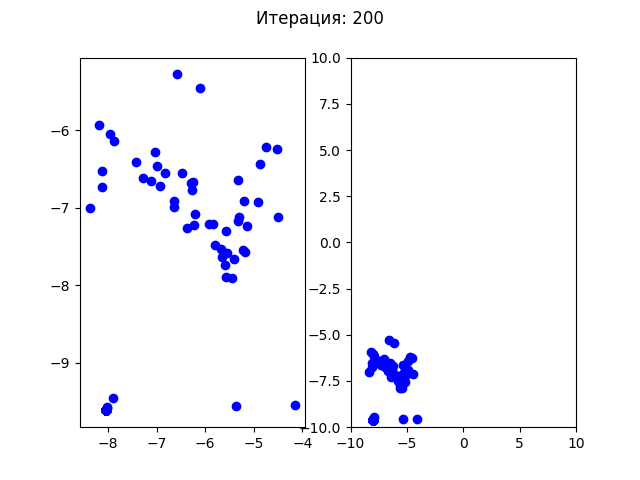
Для теста №2:

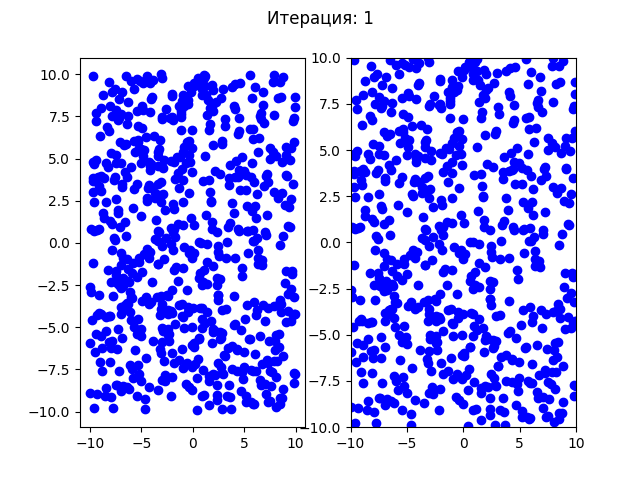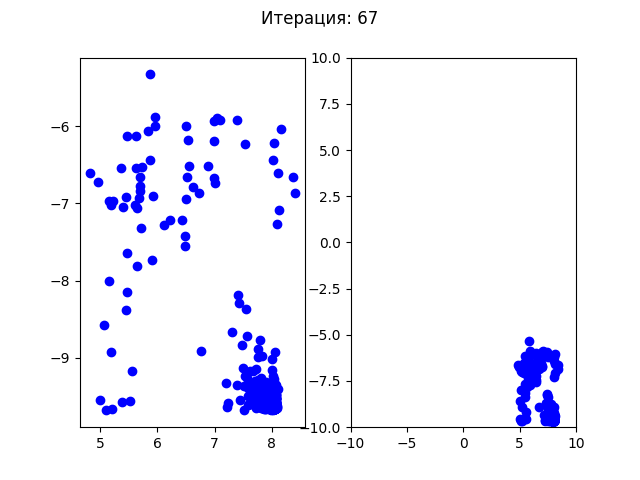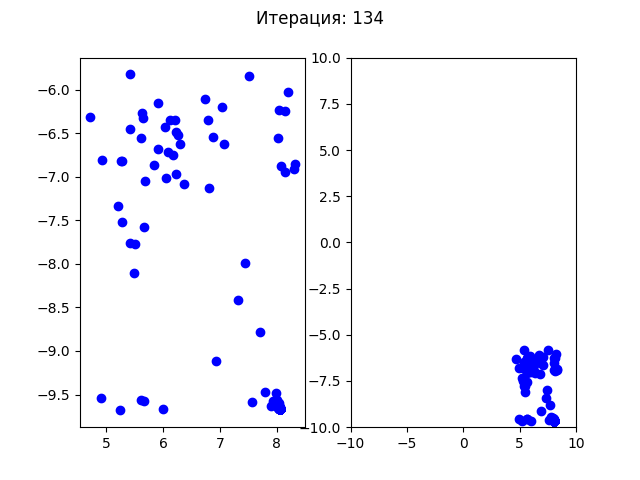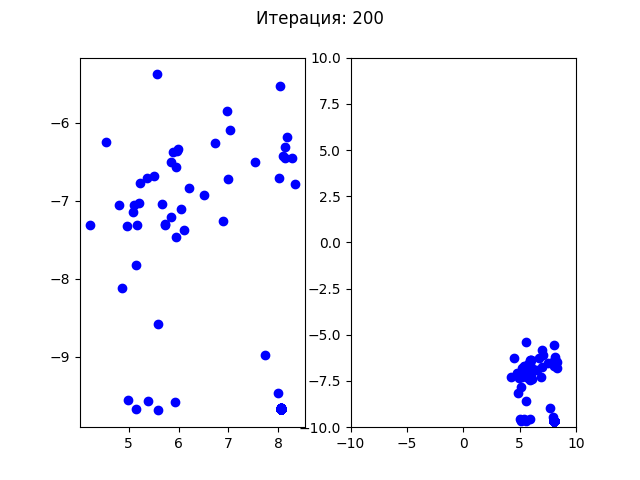
В отличии от генетического алгоритма все частицы начали плавно перемещаться в одну точку. Посмотрим на более простой пример, как сходится генетический алгоритм для функции Экли (у этой функции один минимум в точке (0,0)):

И эта же функция с использованием роя частиц:

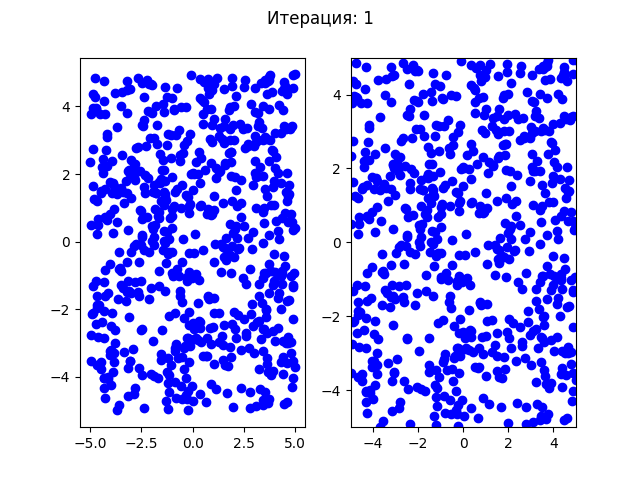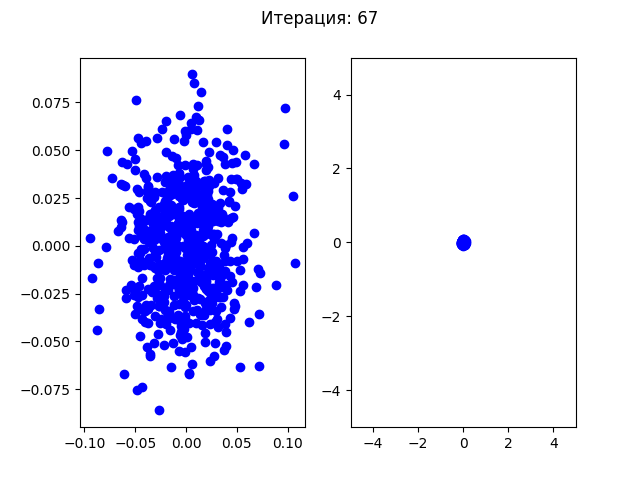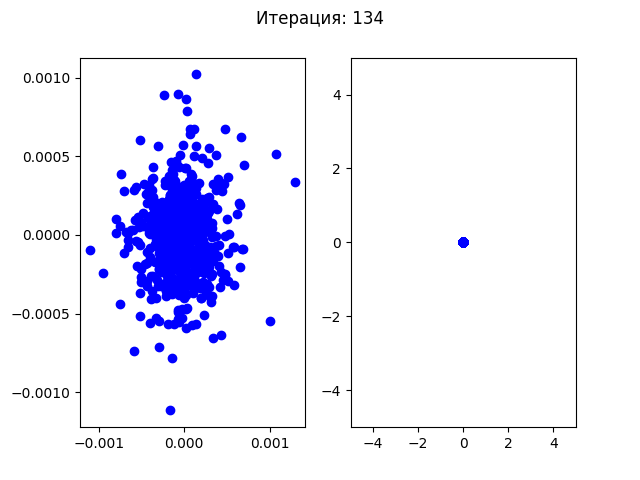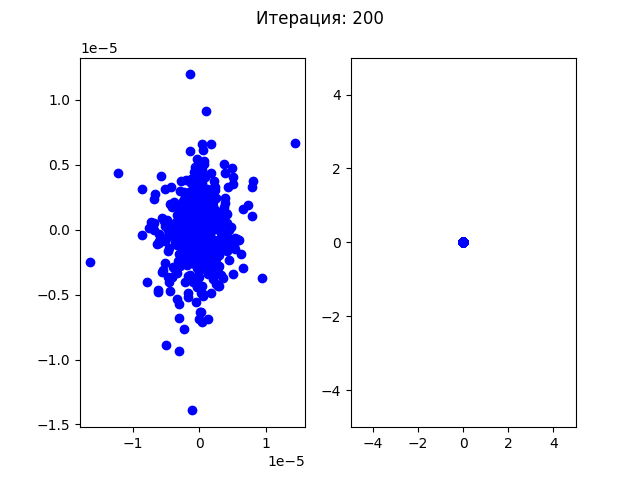
Генетический алгоритм хуже сходится в одну точку, так как каждую новую итерацию в случайной позиции (между родителями) появляется новая особь, а также случайные мутации, которые не всегда могут попадать в нужную точку. Рой частиц плавно приближался к найденному минимуму.

Вывод

Как итог было реализовано и протестировано, как работают два алгоритма оптимизации. Есть еще и другие алгоритмы, например, пчелиный алгоритм, алгоритм иммунной системы и другие. Каждый алгоритм имеет свои плюсы и минусы, некоторые быстрее сходятся в первой найденной точке, другие пытаются найти несколько минимумов и плавно приближаются к каждому из них. Зачастую используют смесь нескольких алгоритмов для того, чтобы избавить один из алгоритмов от имеющихся недочетов.

Ссылочка на гитхаб проекта тут