Заключительный пост №5 для начинающих посвящен сопоставительной визуализации электоральных данных. Предыдущий пост см. здесь.
Сопоставительная визуализация электоральных данных
Теперь рассмотрим набор данных других всеобщих выборов, на этот раз Российских, проходивших в 2011 г. Россия — гораздо более крупная страна, и поэтому данные о проголосовавших на выборах там гораздо объемнее. Для этого мы загрузим в оперативную память один большой TSV-файл с разделением полей данных символом табуляции.
def load_ru():
'''Загрузить данные по России'''
return pd.read_csv('data/ch01/Russia2011.tsv', '\t')Посмотрим, какие имена столбцов имеются в российских данных:
def ex_1_29():
'''Показать список полей электоральных
данных по России'''
return load_ru().columnsБудет выведен следующий список столбцов:
Index(['Код ОИК', 'ОИК №', 'Имя участка',
'Число избирателей, внесенных в список избирателей',
...
'Политическая партия СПРАВЕДЛИВАЯ РОССИЯ',
'Политическая партия ЛДПР - Либерально-демократическая партия России',
'Политическая партия "ПАТРИОТЫ РОССИИ"',
'Политическая партия КОММУНИСТИЧЕСКАЯ ПАРТИЯ КОММУНИСТЫ РОССИИ',
'Политическая партия "Российская объединенная демократическая партия "ЯБЛОКО"',
'Политическая партия "ЕДИНАЯ РОССИЯ"',
'Всероссийская политическая партия "ПАРТИЯ РОСТА"'],
dtype='object')Имена столбцов в российском наборе данных очень описательны, но, пожалуй, длиннее, чем нужно. Также, было бы удобно, если столбцы, представляющие те же самые атрибуты, которые мы уже видели в данных по выборам в Великобритании (к примеру, доля победителя и явка на выборы) были промаркированы одинаковым образом в обоих наборах данных. Переименуем их надлежащим образом.
Наряду с набором данных функция библиотеки pandas rename ожидает словарь, в котором ключам с текущими именами столбцов поставлены в соответствие значения с новыми именами. Если объединить это с данными, которые мы уже рассматривали, то мы получим следующее:
def load_ru_victors():
'''Загрузить данные по России,
выбрать, переименовать и вычислить поля'''
new_cols_dict = {
'Число избирателей, внесенных в список избирателей':'Электорат',
'Число действительных избирательных бюллетеней':
'Действительные бюллетени',
'Политическая партия "ЕДИНАЯ РОССИЯ"':'Победитель'
}
newcols = list(new_cols_dict.values())
df = load_ru().rename( columns=new_cols_dict )[newcols]
df['Доля победителя'] = df['Победитель'] / df['Действительные бюллетени']
df['Явка'] = df['Действительные бюллетени'] / df['Электорат']
return df Библиотека pandas располагает функцией безопасного деления divide, которая идентична операции /, но защищает от деления на ноль. Она вместо пропущенного значения (nan) в одном из полей подставляет значение, передаваемое в именованном аргументе fill_value. Если же оба значения поля равны nan, то результат будет отсутствовать. Поэтому операцию деления можно было бы переписать следующим образом:
df[ 'Доля победителя' ] = \
df[ 'Победитель' ].divide( df[ 'Действительные бюллетени' ], \
fill_value=1 )Визуализация электоральных данных РФ
Мы ранее видели, что гистограмма явки на выборы в Великобритании была приближенно нормально распределенной (хотя и с легкими хвостами). Теперь, когда мы загрузили и преобразовали данные о выборах в России, посмотрим, насколько они сопоставимы:
def ex_1_30():
'''Показать гистограмму
электоральных данных по России'''
load_ru_victors()['Явка'].hist(bins=20)
plt.xlabel('Явка в России')
plt.ylabel('Частота')
plt.show()Приведенный выше пример сгенерирует следующую гистограмму:
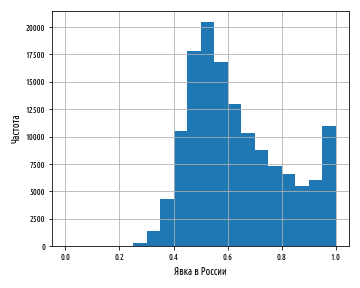
Эта гистограмма совсем не похожа на классические колоколообразные кривые, которые мы видели до сих пор. Имеется явно выраженная положительная асимметрия, и явка избирателей в действительности увеличивается с 80% в сторону 100% — совсем не то, что мы ожидали бы от нормально распределенных данных.
Учитывая ожидания, заданные данными из Британии и центральной предельной теоремой (ЦПТ), такой результат любопытен. Для начала покажем данные на квантильном графике:
def ex_1_31():
'''Показать квантильный график
победителя на выборах в РФ'''
qqplot( load_ru_victors()['Доля победителя'].dropna() )
plt.show()Этот пример вернет следующий график:

На квантильном графике показана линия, которая не является ни прямой, ни одной из S-образных кривых. По существу, квантильный график говорит о наличии легкого хвоста в верхнем конце распределения и тяжелого хвоста в нижнем. Это почти противоположно тому, что мы видим на гистограмме, которая четко указывает на крайне тяжелый правый хвост.
На самом деле, этот квантильный график дезориентирует, и происходит этот именно потому, что хвост очень тяжелый: плотность точек между 0.5 и 1.0 на гистограмме говорит о том, что пик должен составлять порядка 0.7 с последующим правым хвостом за пределами 1.0. Наличие значения, превышающего 100% явно выходит за рамки логики, но квантильный график не объясняет это (он не учитывает, что речь идет о процентах), так что внезапное отсутствие данных за пределами 1.0 интерпретируется как подрезанный правый хвост.
С учетом центральной предельной теоремы и того, что мы наблюдали в данных выборов в Великобритании, тенденция к 100% явке избирателей на выборы выглядит очень любопытно. Давайте выполним параллельный сопоставительный анализ наборов данных по Великобритании и России.
Сравнительная визуализация
Предположим, мы хотели бы сравнить распределение электоральных данных между Великобританией и Россией. Мы уже видели в этой серии постов, как использовать ИФР и коробчатые диаграммы, поэтому теперь займемся исследованием альтернативного варианта, который аналогичен гистограмме.
Мы могли бы попытаться изобразить оба набора данных на гистограмме, но это будет безуспешной затеей, поскольку результаты не поддаются интерпретации по двум следующим причинам:
Размеры избирательных округов, и, следовательно, средних значений распределений сильно отличаются
Абсолютные количества избирательных округов настолько отличаются, что столбцы гистограмм будут иметь разную высоту
Вместо гистограммы альтернативным вариантом, позволяющим решить обе эти задачи, является функция массы вероятности.
Функции массы вероятности
Функция массы вероятности (ФМВ), от англ. Probability Mass Function (PMF), чаще именуемая функцией вероятности дискретной случайной величины, имеет много общего с гистограммой. Однако, вместо того, чтобы показывать количества значений, попадающих в частотные корзины, она показывает вероятность, что взятое из распределения число будет в точности равно заданному значению. Поскольку функция закрепляет вероятность за каждым значением, которое может быть возвращено распределением, и поскольку вероятности измеряются по шкале от 0 до 1, (где 1 соответствует полной определенности), то площадь под функцией массы вероятности равна 1.
Таким образом функция массы вероятности обеспечивает, чтобы площадь под нашими графиками была сопоставимой между наборами данных. Однако у нас все еще имеется одно затруднение — несопоставимость размеров избирательных округов, а значит и средних значений распределений. Это затруднение решается отдельно — при помощи нормализации (или шкалирования).
Существует неисчислимое количество способов нормализации данных, однако один из самых базовых обеспечивает, чтобы каждый числовой ряд находился в интервале от 0 до 1. Ни одно наше значение не находится в отрицательном интервале, поэтому мы можем выполнить нормализацию, попросту разделив каждое индивидуальное значение на самое большое:
def plot_as_pmf(dt, label, ax):
'''График функции вероятности дискретной случайной величины
(или функции массы вероятности)'''
s = pd.cut(dt, bins=40, labels=False) # разбить на 40 корзин
pmf = s.value_counts().sort_index() / len(s) # подсчитать кво в корзинах
newax = pmf.plot(label=label, grid=True, ax=ax)
return newaxИмея в распоряжении приведенную выше функцию, мы теперь можем нормализовать данные по Великобритании и России и изобразить их рядом на тех же осях:
def ex_1_32():
'''Сопоставление данных явки по Великобритании и РФ,
данные нормализованы на основе функции массы вероятностей'''
ax = plot_as_pmf(load_uk_victors()['Явка'], 'Великобритания', None)
plot_as_pmf(load_ru_victors()['Явка'], 'Россия', ax)
plt.xlabel('Интервальные группы явки') # Частотные корзины
plt.ylabel('Вероятность')
plt.legend(loc='best')
plt.show()Приведенный выше пример сгенерирует следующий график:

После нормализации эти два распределения вполне готовы для проведения сопоставительного анализа. Теперь становится совершенно очевидным, каким образом — несмотря на более низкую среднюю явку, чем в Великобритании (0.6366 против 0.6523) — на российских выборах произошел массивный подъем явки близкий к 100%. Поскольку результаты голосования представляют собой объединенный эффект многих независимых волеизъявлений, они ожидаемо будут соответствовать центральной предельной теореме и будут приближенно нормально распределенными. В сущности, за редким исключением, как в Канаде, например, где население имеет гетерогенный характер (там французскоговорящая и англоговорящая группы населения в результате дают бимодальную кривую), результаты выборов по всему миру такому ожиданию обычно соответствуют.
Данные российских выборов показывают чрезвычайно аномальный результат, хотя и не настолько высокий, как модальный пик в центре распределения, который приблизительно соответствует 50% явке. Исследователь Питер Климек (Peter Klimek) и его коллеги в Венском медицинском университете пошли дальше и предположили, что этот результат является явным признаком подтасовки результатов голосования.
Диаграммы рассеяния
Мы обнаружили любопытные результаты, связанные с явкой на ��оссийских выборах и установили, что они имеют сигнатуру, отличающуюся от британских выборов. Теперь посмотрим, каким образом доля голосов за побеждающего кандидата связана с явкой. В конце концов, если неожиданно высокая явка действительно является признаком нечестной игры в пользу действующего президента и правительства, то можно ожидать, что они будут голосовать за себя, а не за кого-либо еще. Таким образом, большинство, если не все, из этих дополнительных голосов ожидаемо будут отданы за итоговых победителей выборов.
Раздел статистики посвященный корреляции довольно подробно рассматривает величины, лежащие в основе взаимосвязи двух переменных, однако на данный момент было бы интересно попросту визуализировать связь между явкой и долей голосов за побеждающую партию.
Заключительный технический прием визуализации, с которым мы познакомим в этом посте, представлен диаграммой рассеяния. Диаграммы рассеяния очень хорошо подходят для визуализации взаимосвязей между двумя переменными: там, где существует линейная взаимосвязь, на графике она будет видна, как диагональная направленность. Библиотека pandas содержит для этого вида графиков функцию scatter с такими же аргументами, что и для функции двумерных графиков plot.
def ex_1_33():
'''Показать диаграмму рассеяния
выборов в Великобритании'''
df = load_uk_victors()[ ['Явка', 'Доля победителей'] ]
df.plot.scatter(0, 1, s=3)
plt.xlabel('Явка')
plt.ylabel('Доля победителя')
plt.show()Приведенный выше пример сгенерирует следующую ниже диаграмму:
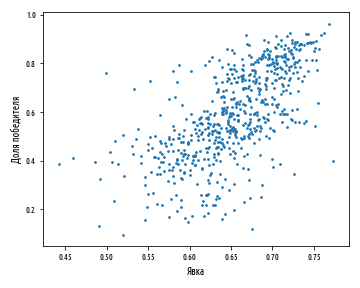
Хотя точки широко разбросаны в виде нечеткого эллипса, четко видна общая диагональная направленность к верхнему правому углу графика рассеяния. Она указывает на интересный результат — явка на выборы коррелирует с долей голосов, отданных за окончательных победителей на выборах, в то время, как ожидалось получить обратный результат: наличия так называемого самодовольства избирателей, которое приводит к более низкой явке в случае, когда победитель гонки очевиден.
Как отмечалось ранее, британские выборы 2010 г. были далеко необычными: они привели к «подвисшему» парламенту и коалиционному правительству. Фактически, «победители» в данном случае представлены обеими сторонами, которые были противниками, вплоть до дня выборов. И поэтому голосование за любую из партий считается как голосование за победителя.
Затем, мы создадим такую же диаграмму рассеяния для выборов в России:
def ex_1_34():
'''Показать диаграмму рассеяния выборов в РФ'''
df = load_ru_victors()[ ['Явка', 'Доля победителя'] ]
df.plot.scatter(0, 1, s=3)
plt.xlabel('Явка')
plt.ylabel('Доля победителя')
plt.show()Этот пример сгенерирует следующую диаграмму:
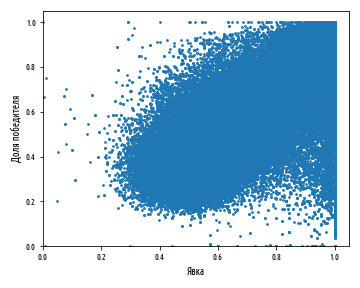
Хотя из расположения точек в данных по России четко прослеживается диагональная направленность, сплошной объем данных затеняет внутреннюю структуру. В последнем разделе этого поста мы покажем простой метод, который позволяет с помощью настройки прозрачности графического изображения вычленять структуру из графиков, подобных этому.
Настройка прозрачности рассеяния
В ситуациях, аналогичных приведенной выше, когда диаграмма рассеяния переполнена точками, можно улучшить визуализацию внутренней структуры данных путем настройки уровня прозрачности. Поскольку наложение полупрозрачных точек будет менее прозрачным, а области с меньшим количеством точек будут более прозрачными, то диаграмма рассеяния с полупрозрачными точками может изобразить плотность данных намного лучше, чем сплошные точки.
Выполнить настройку альфа-канала, регулирующего прозрачность изображаемых на графике pandas точек можно при помощи именованного аргумента alpha в функции scatter в виде числа между 0 и 1, где 1 означает полную непрозрачность, 0 — полную прозрачность.
def ex_1_35():
'''Показать диаграмму рассеяния (с прозрачностью) выборов в РФ'''
df = load_ru_victors()[ ['Явка', 'Доля победителя'] ]
rows = sp.random.choice(df.index.values, 10000)
df.loc[rows].plot.scatter(0, 1, s=3, alpha=0.1)
plt.xlabel('Явка')
plt.ylabel('Доля победителя')
plt.axis([0, 1.05, 0, 1.05])
plt.show()Приведенный выше пример сгенерирует следующую диаграмму:
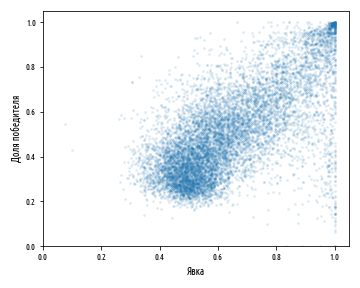
Приведенная выше диаграмма рассеяния показывает общую направленность совместного изменения доли победителя и явки на выборы. Мы видим корреляцию между двумя значениями и «горячую точку» в правом верхнем углу графика, которая соответствует явке близкой к 100% и 100%-ому голосованию в пользу побеждающей стороны. Как раз эта особенность в частности является признаком того, что исследователи из Венского медицинского университета обозначили как сигнатура фальсификации выборов. Этот факт также подтверждается результатами других спорных выборов по всему миру, например, таких как президентские выборы 2011 г. в Уганде.
Результаты многих других выборов по всему миру на уровне округов доступны здесь. На указанном веб-сайте можно получить ссылку на научно-исследовательскую работу и скачать другие наборы данных, на которых можно попрактиковать то, что вы узнали в этой серии постов об очистке и преобразовании реальных данных.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Выводы
Эта серия постов была посвящена сводным статистическим величинам и значениям статистических распределений. Мы увидели, каким образом даже простой анализ может предъявлять свидетельства о потенциальной фальсификационной активности.
В частности, мы познакомились с центральной предельной теоремой и причиной, почему она играет такую важную роль в объяснении широкого применения нормального распределения в исследовании данных. Подходящее статистическое распределение способно всего в нескольких статистиках выразить сущность большой последовательности чисел, некоторые из которых были имплементированы тут на основе встроенных функций языка Python и функций библиотеки scipy. Кроме того, были показаны возможности библиотеки pandas, которая была задействована для загрузки, преобразования и визуального сопоставления нескольких наборов данных. В ходе анализа было обнаружено любопытное расхождение между двумя статистическими распределениями.
Внизу поста можно проголосовать за или против размещения следующей серии постов. Их тема - инференциальная статистика, которая позволяет давать количественную оценку измеренному расхождению между двумя или несколькими статистическими распределениями и принимать решение о статистической значимости этого расхождения. Указанная серия постов также посвящена методам проверки статистических гипотез, которые лежат в основе проведения робастных статистических экспериментов, позволяющих делать выводы на основе имеющихся данных.