
Приглашаю отведать салат из разнородных, но неожиданно связанных друг с другом тем:
Почему нам нравится симметрия и фракталы? И как это влияет на выживаемость?
Как математика связана с эмбриональным развитием?
Сколько старинных программ ещё надо спасти от неумолимого времени?
Конкурс красоты среди фракталов.
А не странно ли, что нам приятно видеть симметричные объекты? Но если симметрии чрезмерно много, то это почему-то начинает раздражать. Возможно, мы найдём в этом смысл, если приблизимся к пониманию вычленяемых мозгом принципов формирования всего вокруг. А для этого мы поиграем с очередным генератором фракталов, в котором удобно творить почти всё: от островов в океане и облаков на небе до кровеносной системы, от галактик до обоев на рабочий стол мельчайших частиц.

Даже в рекомендациях по композиции кадра начинающим фотографам напоминают, что нельзя забывать про симметрию, если хочется сделать приятный снимок. Архитекторы и дизайнеры тоже редко обходятся без симметрии, причём не только из-за физических ограничений мира и требований к оптимальности конструкции, но и ради удовлетворения эстетических предпочтений заказчиков.
А уж если речь заходит о продолжении рода, то большинство почему-то предпочитает людей с симметричными лицами, например. Одно из объяснений этого явления состоит в том, что миллионы лет эволюции научили нас считать несимметричность признаком болезни или опасности. Почему так вышло?
Наш мозг привык легко распознавать правила, по которым построен симметричный объект, поэтому скорее относит его к классу «понятных». Получается, что симметрия — это простота и элегантность, дающие нам экономию усилий. Кроме того, на многих уровнях познания мы видим что-то подобное:

Возможно, миллионы лет естественного отбора научили наш мозг избегать непонятные случайные штуки, из-за чего он и недолюбливает несимметричность. Это могло получиться, потому что в природе кроме беспорядка есть вполне внятные структуры. Соответственно, мы стремимся разглядеть закономерность/симметричность/фрактальность в том, что видим вокруг, чтобы хотя бы мысленно переместиться из реального окружающего нас хаоса во что-то предсказуемое, тем самым почувствовав себя в большей безопасности.

Конечно, маркетологи этим тоже пользуются, см. примеры фотографий с симметричной подачей блюд. Даже немножко раздражает, да?
Почему же мы не любим, когда всё-всё симметрично? Есть предположение, что эволюция и тут всё придумала за нас. Простое объяснение звучит так: в природе мало чрезвычайно симметричных объектов, поэтому мозги к такому просто не привыкли. Соответственно, оказавшись в микрорайоне из одинаковых домиков, мы начинаем паниковать, ведь смотрим на что-то противоестественное.
Другое объяснение можно считать совсем выдуманным из пальца, но какая-то красота и в нём всё же есть. Представьте, как давным-давно неудачники не умели распознавать правила симметрии, поэтому тратили больше ресурсов на понимание простых объектов. Так они проиграли гонку более смышлёным нашим предкам, которые легко видели подобные простые закономерности.
Но далее ситуация продолжила усложняться. Шансы на выживание зависят в том числе и от способности понимать мир. И можно предположить, что те древние люди, которые погрязли в специализации на простейшей симметрии, стали проигрывать нашим предкам, научившимся видеть красоту/смысл/закономерности во фракталах.
Конечно, дело не в распознавании фракталов, а в более развитой способности узнавать и понимать сложные структуры, что критично для выживания. Наши с вами предки видели, что симметрия всё же тривиальна, но они оказались способны разглядеть куда более интересные зависимости. Фракталы, возможно, как раз достигают той самой точки, в которой уже исчезает тривиальность, но ещё сохраняется структура.
Но откуда же кругом в мире симметрия и тем более фракталы?
Для разных объектов есть схожие объяснения. Давайте вникнем в этот вопрос, взглянув через призму крупных пикселей на процесс эмбрионального развития. Заодно лучше прочувствуем, почему кровеносная и нервная системы, а также лёгкие, очень напоминают фракталы. Чтобы ощутить причины самоподобия в организме мы попробуем из одной клеточки восстановить целую Миллу Йовович, как и договаривались в самом начале.
Сразу оговорюсь, что я специально не поставил тэг «Биология», потому что про все эти гомеозисные гены и градиенты концентрации белков-морфогенов понимаю очень поверхностно (желающим погрузиться в этот мир могу рекомендовать «Нужны ли эмбрионам гены?», но начать всё же стоит с Википедии).
Природа не станет зря тратить драгоценные биты на отдельное описание правых и левых конечностей или, например, одинаковых лепестков, поэтому изобрела всякие ловкие механизмы, от которых у специалистов по рефакторингу не только волосы в жилах стынут. Речь о том, что из клетки может развиться многое, но получается мизинец левой ноги, раз уж соседи этой клетки формировали в тот момент именно стопу и именно левой ноги.
Раз так, то давайте поймём, как это всё работает хотя бы в нашей выдуманной модели, а не в настоящем фантастическом фильме.
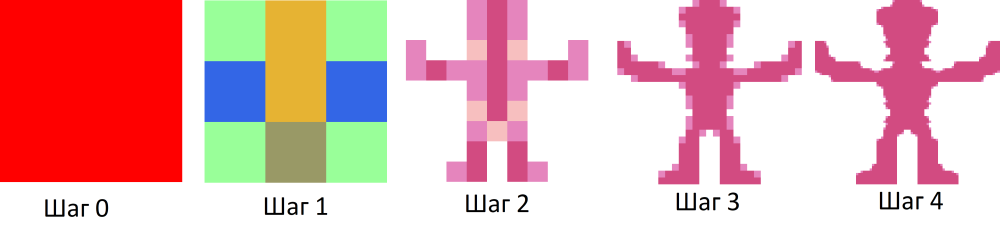
Кстати, поздравляю, мы наконец-то подошли к математике, системам итерируемых функций (про IFS на Хабре ранее было здесь), системам Линденмайера (см. «L-системы и что они себе позволяют» и «L-Systems — математическая красота растений») и всему такому. Ниже ещё будет десяток ссылок для желающих познакомиться ближе, но здесь, чтобы не повторяться, я предлагаю лишь примеры с минимальными пояснениями. Да, у меня нет цели ещё раз изложить многократно описанную теорию. Напротив, мы сейчас занимаемся практикой и построением умеренно корректных аналогий.
Итак, формирование человечка выше выполняется по очень простому принципу — каждая клетка 1x1 заменяется на блок из 3x3 клеток по девяти элементарным правилам:
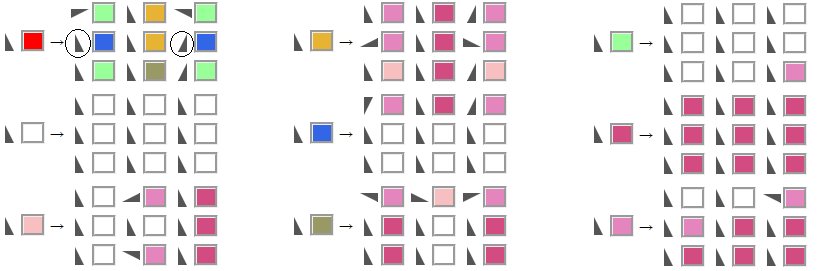
Начинается всё с одной единственной красной клетки, из которой на первом шаге мы получаем две синих (будущие руки), четыре зелёных (будущие кисти и стопы), две жёлтых (голова и туловище) и т.д. Обратите внимание, что рядом с синими квадратиками есть как в зеркало глядящие друг на друга треугольнички (они выделены кружками) — таким образом задаётся ориентация этих двух клеток, чтобы из них в будущем получились симметричные конечности.
Далее это всё продолжает делиться, становясь всё более гладким и человекообразным. Например, на втором шаге синие клетки (будущие руки) по центральному правилу превращаются в последовательность из розовой-красной-розовой клеток, под которыми шесть белых (пустых) ячеек. Затем красные клетки будут оставаться красными навсегда (т.е. заменяться на блок из 3x3 таких же красных клеток). Короче, всё как у людей, только гены заменены на весёлые картинки.
Вместо чтения словесного описания запустите генератор с этими правилами! Просто пройдите по ссылке, чтобы разглядеть процесс развития человечка на всех этапах. Меняя параметр Depth, вы задаёте количество итераций. Слева палитра цветов и ориентаций, а рядом с нею все правила, которые можно свободно менять. И сразу всё станет ясно!
Получается, что этот набор правил можно считать аналогом ДНК, определяющим развитие организма на протяжении произвольного количества итераций. В текстовом виде инструкции для построения человечка записываются также коротко:
{"depth":3,"n":3,"rules":[[106,3,706,4,3,404,6,5,406], [1,1,1,1,1,1,1,1,1], [1,308,7,1,1,7,1,708,7], [8,7,408,308,7,508,2,7,402], [608,7,408,1,1,1,1,1,1], [708,502,108,7,1,7,7,1,7], [1,1,1,1,1,1,1,1,8], [7,7,7,7,7,7,7,7,7],[1,1,708,8,7,7,7,7,7]], "colors":["#ff0000", "#ffffff", "#f7bfbf", "#E6B333", "#3366E6", "#999966", "#99FF99", "#d24b81", "#e585bd"]}
Другой пример перистых облаков устроен ещё проще: всего три правила на матрицах 2x2:

Да, оказалось, что всего трёх простых правил хватает, чтобы построить несимметричную, но вполне регулярную конструкцию, которую глазом легко отличить от хаоса. В окружающем нас мире подобного много, что и неудивительно, учитывая элементарность правил.
Опять же, тут мы имеем очень короткий JSON с текстовым описанием, а поиграть с этим фракталом можно тут:{"depth":10,"n":2,"rules":[[200,1,100,600],[1,102,100,100],[2,102,2,2]],"colors":["#9fbae9","#735cc7","#ffffff"]}
Любители классической математики могут вспомнить общеизвестный ковёр Серпинского (как обычно, по этой ссылке откроется генератор, в котором можно менять все параметры и правила):

Такой ковёр при бесконечном количестве итераций хоть и имеет бесконечный периметр, нулевую площадь, а также дробную размерность (ln 8/ln 3 ~ 1,89), но всё же глазу не кажется особо интересным, поскольку он одинаковый и понятный во все стороны. Как было показано выше, самое разнообразное и красивое происходит, если доворачивать и отражать треугольнички ориентации клеток. Попробуйте! Ещё несколько примеров с пояснениями есть здесь, но я бы рекомендовал сперва попытаться создать свой фрактал, потому что тогда всё сразу гораздо яснее станет.
История генератора фракталов и благодарности
Идея реализовать эту систему возникла после встречи со старинной программой Changer2 (1997 Юрий Хан, лицензия CC0 v.1.0 или старше), которая основана на ещё более давней программе Changer (её найти не удалось, но есть свидетельства, что сделал её Евгений Кашменский). Программа Changer2 реализована больше двух десятилетий назад, так что для её запуска может понадобиться старая версия Windows или эмулятор. Примерно так это всё раньше выглядело (здесь же виден пример симпатичного фрактала):
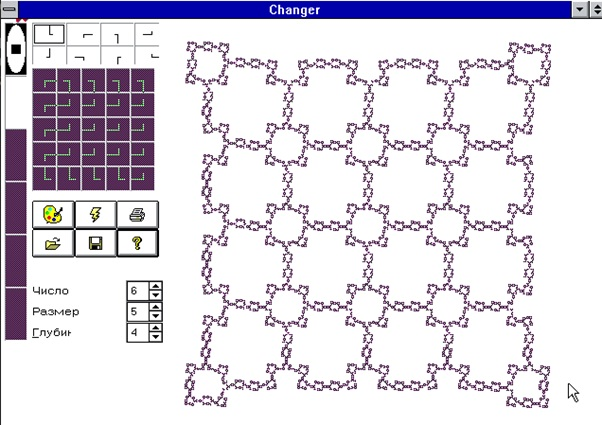
В очередной раз запустив эту чудесную программу, я вспомнил о том, как добрые люди недавно спасли прекрасную японскую игру «Jelly no Puzzle» (выглядела она как-то так). Они перенесли основную логику в браузер. Да, пропала анимация и музыка, но продуманные уровни сохранены, а это важнее.
Увы, многие замечательные программы уходят, потому что, как бы нелепо это ни звучало, современные компьютерные системы для них не подходят. Профессионал запустит что угодно в эмуляторе, но большинство остаётся без древних волшебных программ. Прогресс неумолим, так что нам остаётся только успевать спасать то, что лично нам нравится и кажется правильным. А какую программу из своего детства вы бы хотели воскресить, чтобы поделиться с потомками?

Я постарался повторить Changer2 в браузере, чтобы современные дети от 7 до 107 лет смогли приобщиться к исследованию фракталов ещё и таким образом. Если формулировать мечту совсем серьёзно, то я хотел предложить детям среду для эстетически-математических экспериментов, а через 30-40 лет случайно узнать, что один из нобелевских лауреатов в своей речи вспоминает, как заинтересовался наукой, играя с генератором фракталов с Хабра, но уже не помнит, с каким.
Да, это для детей! И для всех нас. Здесь можно было бы ещё рассказать про борьбу за производительность и JavaScript (изначально генератор строил картинку 1024x1024 несколько секунд, а сейчас работает почти мгновенно даже на телефонах). Но скажем прямо, оптимизации там очевидные, поэтому давайте сразу перейдём к веселью!
Конкурс красоты среди фракталов
Эксперименты на живых людях показали, что в этом генераторе фракталов удаётся строить самые неожиданные конструкции. Поэтому я приглашаю вас попробовать создать что-то предельное: радующее глаз и поражающее простотой правил, но удивляющее замыслом и не дающее покоя.
Делитесь в комментариях ссылками на свои фракталы, а также изображениями с интересными их фрагментами. А ещё, пожалуйста, проголосуйте за понравившиеся фракталы в чужих комментариях, чтобы коллективное и бессознательное Хабра выбрало самый красивый фрактал!
Ссылки
Если вам интересна эта статья, то, вероятно, коллекция ссылок тоже порадует:
Почему просмотр фракталов успокаивает (про картины Поллока и работу глаз);
Кош на комплексной плоскости (дробно-линейные преобразования комплексной плоскости);
Трилогия Фракталы в простых числах, Фракталы в иррациональных числах и Фракталы в иррациональных числах-2;
Ночь фракталов (Random IFS, потом kNN, а затем Escape-Time Algorithm);
Основы фрактального сжатия изображений (наконец-то ответ на вопрос о практической применимости фракталов; впрочем, бывают ещё фрактальные антенны).
Присылайте свои фракталы в комментарии! Полный адрес фрактала можно взять как в адресной строке браузера, так и скопировав его из ссылки «Link to this configuration» на странице генератора. Изображение же проще всего получить, выбрав пункт «Copy image» или «Save image as...» в контекстном меню сгенерированной картинки. Кнопка «Back» браузера работает как «Undo», так что вы всегда сможете откатиться на предыдущее состояние своего набора правил. Если попробуете построить изображение больше, чем 2200x2200 точек, то система переспросит, так как это всё же может быть долго (для работы в таком высоком качестве рекомендую отключить автоматическую перерисовку).