Катран, или морская собака (Squalus acanthias) – достаточно широко распространенная акула, относящаяся к роду колючих акул и семейству Катрановые акулы из отряда Катранообразные. Обитатель умеренных вод бассейнов всех мировых океанов, как правило, встречается на глубине не более 1460 метров. На сегодняшний день максимальной зарегистрированной является длина тела в пределах 160-180 см.
Эта рыбка будет хорошим примером для начала изучения пакета гидродинамического моделирования WaterLily.jl.
В этой заметке будет показано, как создать и запустить модель плывущего катрана, используя язык Julia и пакет WaterLily.jl. Этот пост адаптирован из блокнота Pluto, который вы можете скачать здесь.
using WaterLily, StaticArrays, PlutoUI, Interpolations, Plots, ImagesМы будем использовать простую модель акулы, основанную на новаторской работе Лайтхилла о плавании стройных рыб. При построении модели внимание сосредоточено на "хребте" рыбы, идеализируя форму как распределение толщины относительно оси симметрии, а движение как латеральную ("из стороны в сторону") бегущую волну. Удивительно, но этот простой подход дает представление об огромном диапазоне плавающих животных, как показано на рисунке ниже.
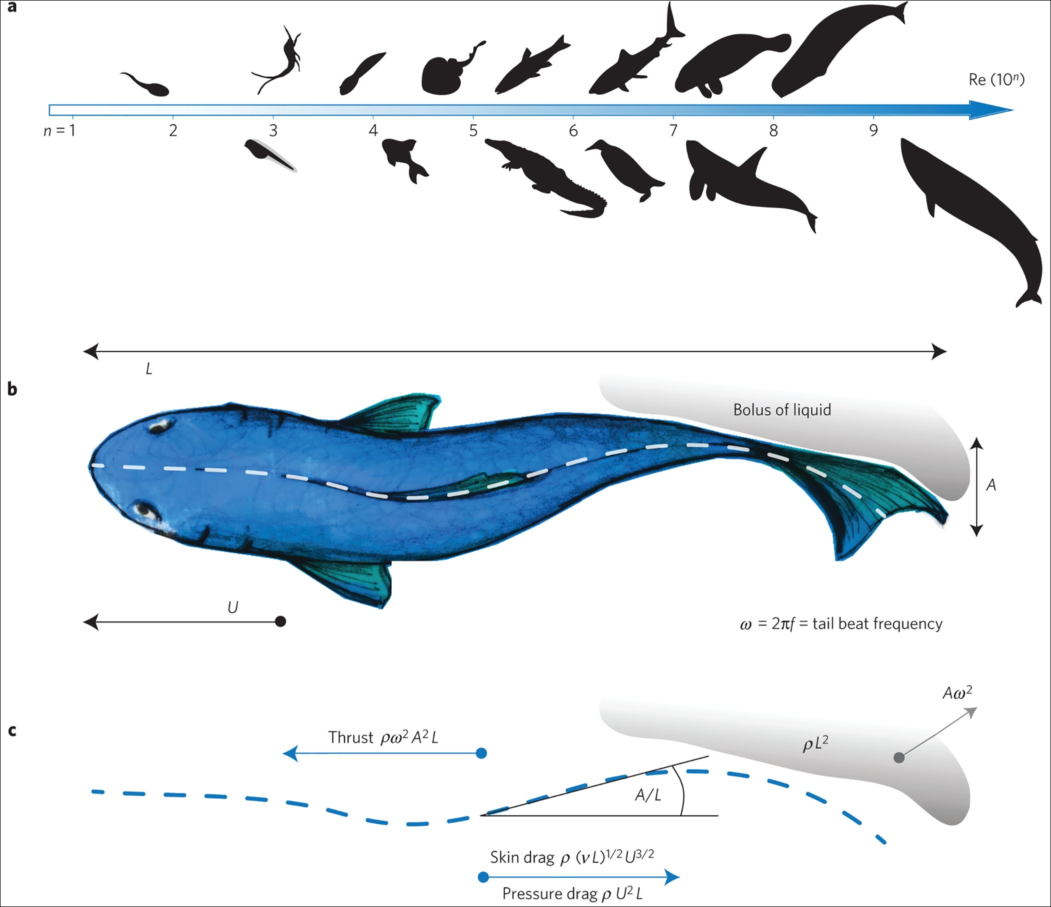
Тело и динамика
Мы определим контур тела (распределение толщины) задав несколько опорных точек и проведя интерполяцию сплайнами.
fit = y -> scale(
interpolate(y, BSpline(Quadratic(Line(OnGrid())))),
range(0,1,length=length(y))
)Скачаем картинку по которой будем создавать модель. Права на изображение принадлежат Shark Trust.
url2="https://pterosaurheresies.files.wordpress.com/2020/01/squalus-acanthias-invivo588.jpg"
filename2 = download(url2)
dogfish = load(filename2)
Чтобы задать функцию распределения толщины thk, определим ширину рыбины в нескольких местах
plot(dogfish)
nose, len = (30,224), 500
width = [0.02, 0.07, 0.06, 0.048, 0.03, 0.019, 0.01]
scatter!(
nose[1] .+ len .* range(0, 1, length=length(width)),
nose[2] .- len .* width, color=:blue, legend=false)
thk = fit(width)
x = 0:0.01:1
plot!(
nose[1] .+ len .* x,
[nose[2] .- len .* thk.(x), nose[2] .+ len .* thk.(x)],
color=:blue)Глядя на видеозаписи плавающих акул-собак, мы можем заметить несколько общих черт:
Движение передней половины тела имеет небольшую амплитуду (около 20% от движения хвоста). Это задает огибающую амплитуды для бегущей волны.
envelope = [0.2,0.21,0.23,0.4,0.88,1.0]
amp = fit(envelope)Длина волны пробегающей по хребту рыбы немного больше длины тела
В приведенном ниже коде вы можете изменять значение λ для управления длиной бегущей волны, чтобы увидеть, какое влияние она оказывает на позвоночник в течение цикла движения.
λ = 1.4
scatter(0:0.2:1, envelope)
colors = palette(:cyclic_wrwbw_40_90_c42_n256)
for t in 1/12:1/12:1
plot!(x, amp.(x) .* sin.(2π/λ * x .- 2π*t),
color=colors[floor(Int,t*256)])
end
plot!(ylim=(-1.4,1.4), legend=false)Настройка моделирования
Тело и механика движения готовы, но как мы применим их к моделированию жидкости? WaterLily использует метод погруженной границы (Метод погруженной границы для чайников) и автоматическое дифференцирование (Автоматическое дифференцирование для чайников) для внедрения тела в поток. В итоге все, ч��о нам нужно, это функция расстояния до поверхности (SDF).
Давайте начнем с определения SDF для "позвоночника", который является отрезком прямой от 0 до 1 по х. Посмотрите замечательное видео от Inigo Quilez про вывод sdf. На графике ниже показаны sdf и нулевой контур, который ... есть просто отрезок линии.
Простые корректировки SDF дают нам контроль над формой и положением. Изменив значение y а ля y = y-shift, мы можем переместить тело вбок. А вычитая из длины контура толщину, как sdf = sdf-thickness, мы можем придать линии некоторую ширину. Это все, что нам нужно для моделирования акулы.
shift = 0.5
T = 0.5
function segment_sdf(x, y)
s = clamp(x, 0, 1) # distance along the segment
y = y - shift # shift laterally
sdf = √sum(abs2, (x-s, y)) # line segment SDF
return sdf - T * thk(s) # subtract thickness
end
grid = -1:0.05:2
contourf(grid, grid, segment_sdf, clim=(-1,2), linewidth=0)
contour!(grid, grid, segment_sdf, levels=[0], color=:black) # zero contourПосле того, как проверен вид нашей SDF, мы готовы к созданию симуляции WaterLily с помощью функции fish, определенной ниже:
В качестве аргументов принимаются функции
thkдля создания sdf и функцияampдля создания карты бегущей волны.Единственным числовым параметром, передаваемым в
fish, является длина рыбыL, измеряемая в расчетных ячейках. Она задает разрешение моделирования и размер массивов жидкости.Другими параметрами являются амплитуда для хвоста
Aкак доля длины, число Струхаля, задающее частоту движенияω, и число Рейнольдса, задающее вязкость жидкостиν.
function fish(thk, amp, k=5.3; L=2^6, A=0.1, St=0.3, Re=1e4)
# fraction along fish length
s(x) = clamp(x[1]/L, 0, 1)
# fish geometry: thickened line SDF
sdf(x,t) = √sum(abs2, x - L * SVector(s(x), 0.)) - L * thk(s(x))
# fish motion: travelling wave
U = 1
ω = 2π * St * U/(2A * L)
function map(x, t)
xc = x .- L # shift origin
return xc - SVector(0., A * L * amp(s(xc)) * sin(k*s(xc)-ω*t))
end
# make the fish simulation
return Simulation((4L+2,2L+2), [U,0.], L;
ν=U*L/Re, body=AutoBody(sdf,map))
end
# Create the swimming shark
L,A,St = 3*2^5,0.1,0.3
swimmer = fish(thk, amp; L, A, St);
# Save a time span for one swimming cycle
period = 2A/St
cycle = range(0, 23/24*period, length=24)Мы можем проверить нашу геометрию, построив график погруженной граничной функции μ₀, которая равна 1 в жидкости и 0 внутри плавающего тела.
@gif for t ∈ cycle
measure!(swimmer, tswimmer.L/swimmer.U)
contour(swimmer.flow.μ₀[:,:,1]',
aspect_ratio=:equal, legend=false, border=:none)
end
Выполнение визуализации
Анимация движения выглядит отлично, так что мы готовы запустить симулятор потока!
Функция sim_step!(sim, t, remeasure=true) запускает симулятор до момента времени t, повторно измеряя положение тела на каждом временном шаге. (по умолчанию remeasure=false, так как это требует дополнительного времени на вычисления и не нужно для статических геометрий).
# run the simulation a few cycles (this takes few seconds)
sim_step!(swimmer, 10, remeasure=true)
sim_time(swimmer)Симуляция отработала, но по умолчанию нет никаких визуализаций или измерений.
Чтобы понять, что происходит, давайте изобразим вихри ω=curl(u) порождаемые при движении акулы. Для этого необходимо смоделировать цикл движения и вычислить завихрения во всех точках макросом @inside.
# plot the vorcity ω=curl(u) scaled by the body length L and flow speed U
function plot_vorticity(sim)
@inside sim.flow.σ[I] = WaterLily.curl(3, I, sim.flow.u) * sim.L / sim.U
contourf(sim.flow.σ',
color=palette(:BuGn), clims=(-10, 10), linewidth=0,
aspect_ratio=:equal, legend=false, border=:none)
end
# make a gif over a swimming cycle
@gif for t ∈ sim_time(swimmer) .+ cycle
sim_step!(swimmer, t, remeasure=true)
plot_vorticity(swimmer)
end
Красивое... (в конце концов, CFD означает Colorful Fluid Dynamics). Анимация также говорит нам кое-что важное о потоке. Обратите внимание, что от тела не отходят вихри нигде, кроме хвоста! Это признак эффективности, поскольку энергия расходуется только на создание этих вихрей.
Покопаемся еще и получим некоторые количественные измерения из моделирования. Функция ∮nds берет интеграл по поверхности тела. Зная давление p, мы можем измерить силу тяги и периферическую силу создаваемую акулой!
function get_force(sim, t)
sim_step!(sim, t, remeasure=true)
return WaterLily.∮nds(sim.flow.p, sim.body, t*sim.L/sim.U) ./ (0.5*sim.L*sim.U^2)
end
forces = [get_force(swimmer, t) for t ∈ sim_time(swimmer) .+ cycle]
scatter(cycle./period, [first.(forces), last.(forces)],
labels=permutedims(["thrust", "side"]),
xlabel="scaled time",
ylabel="scaled force")
Мы можем многое узнать из этого простого графика. Например, латеральная сила (действующая из стороны в сторону) имеет ту же частоту, что и само плавательное движение, в то время как сила тяги имеет вдвое большую частоту, с пиком каждый раз, когда хвост проходит через центральную линию.
Следующие шаги
Эта простая модель - отличное начало, и она открывает тонну возможностей для улучшения симуляции акулы и предложения вопросов для исследования:
Мгновенные силы должны быть равны нулю в свободно плавающем теле! Для этого мы можем добавить в нашу модель движения реакции. Будет ли модель акулы плыть по прямой, если мы сделаем это, или необходим цикл управления?
Настоящие акулы куда трехмерней. Хотя мы можем легко обобщить э��от подход, используя двумерные сплайны, моделирование займет гораздо больше времени. Есть ли способ использовать GPU для ускорения моделирования без полного изменения солвера?
Если бы мы собирались сделать робота вдохновленного биомеханикой акулы, у нас были бы ограничения на форму, движение и доступное питание. Можем ли мы использовать эту структуру для оптимизации нашей робототехники в рамках имеющихся ограничений?
Ниже приведены ссылки на все пакеты, используемые в этом блокноте. Счастливого моделирования!