Введение
В своей предыдущей статье я описал способ нахождения делимого вероятности выпадения какой-то суммы чисел на кубиках при помощи многократной свёртки последовательности [1 1 1 1 1 1] на саму себя. Иными словами, многократное умножение в столбик (без переноса переполнившихся разрядов) последовательности/числа 111111 на саму/само себя. Почему, правда, не пишут, что умножение в столбик является прямой аналогией свёртки последовательностей — для меня загадка (может я что-то упускаю из вида - если я не прав, пожалуйста, напишите). Однако, дальше в статье я буду применять два словосочетания "свёртка последовательностей" и "умножение в столбик" совместно, т.к. первое — корректное описание операции, а второе отвечает за наглядность и простоту восприятия.
Напомню:
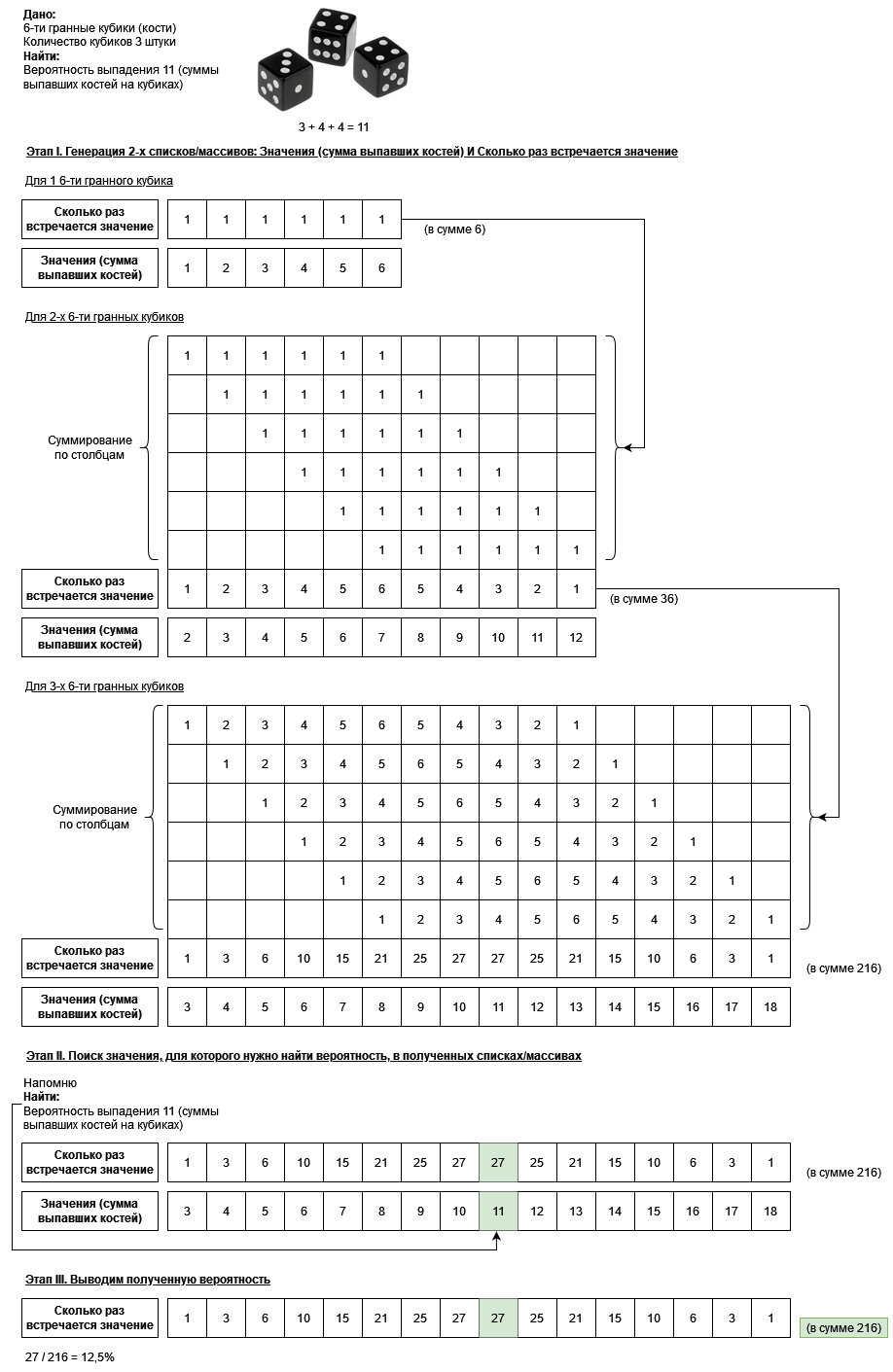
Так же в конце предыдущей статьи я "страшился" найти вероятности для 1000 кубиков. Вот именно этим и предлагаю заняться.
Прелюдия
Хотелось бы подчеркнуть, что и на картинке вверху, и собственно в предыдущей статье упор делался на "умножение в столбик" / свёртку последовательностей [1 1 1 1 1 1], и не затрагивалась возможность "умножить" на что-либо ещё. Вот эту оплошность хотелось бы упразднить.
Отвлекусь немного на факт, что любое натуральное число может быть представлено как сумма натуральных степеней числа 2 (Производящие функции — туда и обратно ответ на вопрос: какие грузы можно взвесить с помощью гирь в 20, 21, 22,..., 2n грамм и сколькими способам?). Приведу визуализацию:
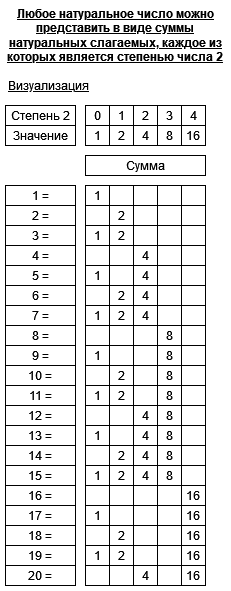
Данное знание нам будет полезно для операций со степенями. Например, нахождение какого-то числа a63 будем представлять как: a63 = a1 + 2 + 4 + … + 32 = a1 * a2 * a4 * … * a32. То есть зная только I эл��мент и умея умножать/свёртывать будем пытаться найти 63-й элемент (степень 63) используя как можно меньше операций умножения/свёртки.
Для начала хотелось бы обкатать операцию свёртки последовательностей / "умножение в столбик" на уже знакомом треугольнике Паскаля. А именно попробовать найти 9-й элемент треугольника Паскаля зная только I элемент (именно [1 1]) не при помощи многократной свёртки последовательностей / "умножение в столбик" [1 1] на саму себя (дискретная свёртка или полиномиальное умножение), а представив что каждая последовательность чисел в треугольнике Паскаля соответствует степени последовательности [1 1]. Звучит наверно запутанно, так что приведу картинку из прошлой статьи, для визуализации:
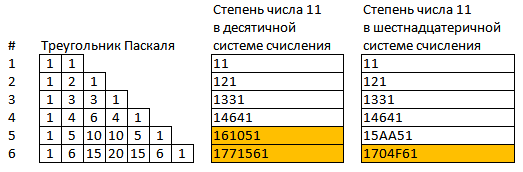
Попробуем найти 9-й элемент треугольника Паскаля.
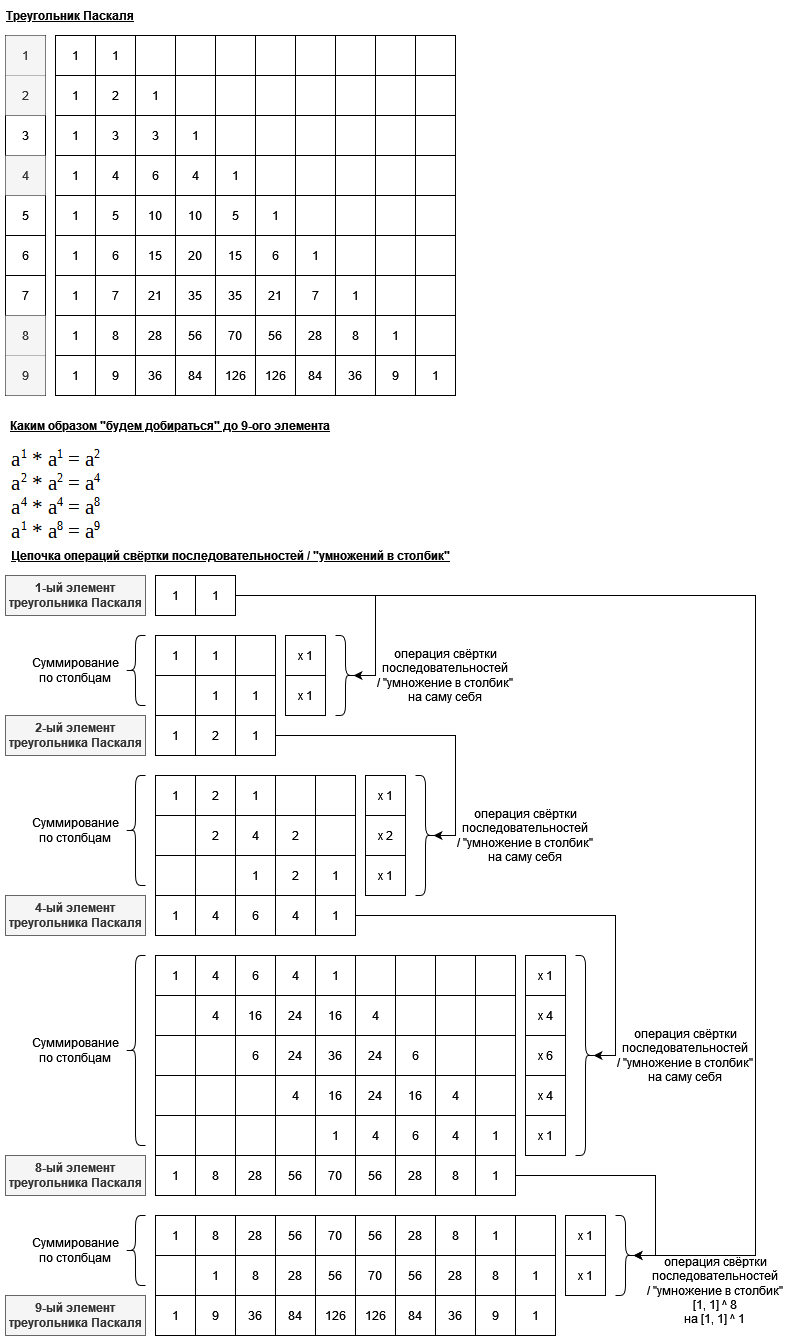
Выглядит многообещающе. Так же приложу скрипт с теми же результатами при помощи именно свёртки последовательностей.
Python. Пример. II, IV, VIII, XI элемент треугольника Паскаля
# -*- coding: utf-8 -*-
import numpy
convolve_out = numpy.convolve([1, 1], [1, 1])
# [1 2 1]
print(convolve_out)
convolve_out = numpy.convolve(convolve_out, convolve_out)
# [1 4 6 4 1]
print(convolve_out)
convolve_out = numpy.convolve(convolve_out, convolve_out)
# [ 1 8 28 56 70 56 28 8 1]
print(convolve_out)
convolve_out = numpy.convolve(convolve_out, [1, 1])
# [ 1 9 36 84 126 126 84 36 9 1]
print(convolve_out)
Визуализация алгоритма, I попытка
По аналогии с треугольником Паскаля хочется провернуть аналогичную операцию с кубиками, и найти для примера вероятность выпадения суммы костей 19 для 5 кубиков. Т.е. возьмём первоначальную последовательность [1 1 1 1 1 1] и дойдём до 5-ого кубика (степень 5) по следующей цепочке операций свёртки последовательностей / "умножение в столбик":
a1 * a1 = a2
a2 * a2 = a4
a1 * a4 = a5

Приложу скрипт для нахождения “Сколько раз встречается значение” в “Этап I. Генерация 2-х списков/массивов: Значения (сумма выпавших костей) И Сколько раз встречается значение” при помощи свёртки последовательностей / “умножения в столбик”.
Python. Пример. Свёртка последовательностей [1 1 1 1 1 1]
# -*- coding: utf-8 -*-
import numpy
convolve_out = numpy.convolve([1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1])
# [1 2 3 4 5 6 5 4 3 2 1]
print(convolve_out)
convolve_out = numpy.convolve(convolve_out, convolve_out)
# [ 1 4 10 20 35 56 80 104 125 140 146 140 125 104 80 56 35 20 10 4 1]
print(convolve_out)
convolve_out = numpy.convolve(convolve_out, [1, 1, 1, 1, 1, 1])
# [ 1 5 15 35 70 126 205 305 420 540 651 735 780 780 735 651 540 420 305 205 126 70 35 15 5 1]
print(convolve_out)
Скрипты, I попытка
В целом, как мне кажется, задумка достаточно расписана. Остаётся выложить получившейся скрипты, написанные по описанным лекалам. Простор для оптимизаций оставляю читателям.
Python
# -*- coding: utf-8 -*-
def main():
c_int_side_dice: int = 6 # сколько граней у кубика
c_int_dice_number: int = 1000 # кол-во кубиков
c_int_number_to_find: int = 2000 # число, вероятность выпадения которого хотим найти
probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
print(probability)
# собственно поиск вероятности определённого значения
def dice_probability(int_dice_number: int, int_number_to_find: int, c_int_side_dice: int) -> float:
if int_number_to_find >= int_dice_number and int_number_to_find <= c_int_side_dice * int_dice_number:
list_values: list[int] = [i for i in range(int_dice_number, c_int_side_dice * int_dice_number + 1)]
list_interm_probability = interm_probabilities(c_int_side_dice, int_dice_number)
for i in range(len(list_values)):
if list_values[i] == int_number_to_find:
int_out: int = list_interm_probability[i]
break
return int_out / (c_int_side_dice ** int_dice_number)
else:
# задаваемое число выходит за рамки реально возможного диапазона значений
return 0.0
# возвращает список/массив: сколько раз встречается значение
def interm_probabilities(int_side_dice: int, int_pow: int) -> list[int]:
"""
На примере int_side_dice = 6, int_pow = 5
{
1: [1, 1, 1, 1, 1, 1],
2: [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1],
4: [1, 4, 10, 20, 35, 56, 80, 104, 125, 140, 146, 140, 125, 104, 80, 56, 35, 20, 10, 4, 1]
5: [1, 5, 15, 35, 70, 126, 205, 305, 420, 540, 651, 735, 780, 780, 735, 651, 540, 420, 305, 205, 126, 70, 35, 15, 5, 1]
}
"""
dict_interm_probability: dict[int, list[int]] = {1: [1] * int_side_dice}
if int_pow == 0:
print("Не поддерживается")
quit()
elif int_pow != 1:
list_to_do = map_todo(int_pow)
for elem in list_to_do:
dict_interm_probability[elem[2]] = multiply_cins_orig(dict_interm_probability[elem[0]], dict_interm_probability[elem[1]])
return dict_interm_probability[int_pow]
# Как добраться до интересующего значения, используя x2/+nx для степеней
def map_todo(int_wanted: int) -> list[tuple[int, int, int]]:
"""
На примере int_wanted = 5
Степени "числа":
1
1 * 2 = 2 -> tuple(1, 1, 2)
2 * 2 = 4 -> tuple(2, 2, 4)
4 + 1 = 5 -> tuple(4, 1, 5)
"""
int_current_id: int = 1
int_sum: int = 1
b_ascending: bool = True
list_solution: list[tuple[int, int, int]] = []
while True:
if int_sum == int_wanted:
break
elif b_ascending and 2 * int_current_id <= int_wanted:
list_solution.append( # mult_1, mult_2, result
(int_current_id, int_current_id, 2 * int_current_id)
)
int_current_id = 2 * int_current_id
int_sum = int_current_id
elif b_ascending and 2 * int_current_id > int_wanted:
b_ascending = False
int_sum = int_current_id
int_current_id = int(int_current_id / 2) # чтобы возвращал именно integer
elif not b_ascending and int_sum + int_current_id <= int_wanted:
list_solution.append( # mult_1, mult_2, result
(int_sum, int_current_id, int_sum + int_current_id)
)
int_sum = int_sum + int_current_id
int_current_id = int(int_current_id / 2) # чтобы возвращал именно integer
elif not b_ascending and int_sum + int_current_id > int_wanted:
int_current_id = int(int_current_id / 2) # чтобы возвращал именно integer
return list_solution
# "умножение" в столбик двух массивов/списков
def multiply_cins_orig(list_in_1: list[int], list_in_2: list[int]) -> list[int]:
int_len_2: int = len(list_in_2)
list_dummy: list[list[int]] = []
for i in range(int_len_2):
list_dummy.append([0] * i) # [], [0], [0, 0], [0, 0, 0] ...
list_for_sum: list[list[int]] = []
i: int = -1
for elem_2 in list_in_2:
i += 1
list_interm: list[int] = [elem_1 * elem_2 for elem_1 in list_in_1]
list_for_sum.append(list_dummy[i] + list_interm + list_dummy[int_len_2 - i - 1])
"""
[list_in_1 X elem_2[0], 0, 0, 0, 0, 0]
[0, list_in_1 X elem_2[1], 0, 0, 0, 0]
[0, 0, list_in_1 X elem_2[2], 0, 0, 0]
[0, 0, 0, list_in_1 X elem_2[3], 0, 0]
[0, 0, 0, 0, list_in_1 X elem_2[4], 0]
[0, 0, 0, 0, 0, list_in_1 X elem_2[5]]
"""
list_out: list[int] = []
for i in range(len(list_for_sum[0])):
sum_out: int = 0
for j in range(int_len_2):
sum_out += list_for_sum[j][i]
list_out.append(sum_out)
"""
[1, 3, 6, 10, 15, 21, 25, 27, 27, 25, 21, 15, 10, 6, 3, 1]
"""
return list_out
main()
JavaScript
function main(){
const c_int_side_dice = 6; // сколько граней у кубика
const c_int_dice_number = 100; // кол-во кубиков
const c_int_number_to_find = 300; // число, вероятность выпадения которого хотим найти
let probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice);
console.log(probability);
}
// собственно поиск вероятности определённого значения
function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice){
if (int_number_to_find >= int_dice_number && int_number_to_find <= c_int_side_dice * int_dice_number){
let list_values = new Array();
let i = 0;
for (let j = int_dice_number; j <= c_int_side_dice * int_dice_number; j++){
list_values[i] = j;
i++;
}
let list_interm_probability = interm_probabilities(c_int_side_dice, int_dice_number);
let int_out;
for (let i = 0; i <= list_values.length; i++){
if (list_values[i] == int_number_to_find){
int_out = list_interm_probability[i];
break;
}
}
return int_out / Math.pow(c_int_side_dice, int_dice_number);
} else {
// задаваемое число выходит за рамки реально возможного диапазона значений
return 0.0;
}
}
// возвращает список/массив: сколько раз встречается значение
function interm_probabilities(int_side_dice, int_pow){
// На примере int_side_dice = 6, int_pow = 5
// {
// 1: [1, 1, 1, 1, 1, 1],
// 2: [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1],
// 4: [1, 4, 10, 20, 35, 56, 80, 104, 125, 140, 146, 140, 125, 104, 80, 56, 35, 20, 10, 4, 1]
// 5: [1, 5, 15, 35, 70, 126, 205, 305, 420, 540, 651, 735, 780, 780, 735, 651, 540, 420, 305, 205, 126, 70, 35, 15, 5, 1]
// }
let dict_interm_probability = {1: Array(int_side_dice).fill(1)};
if (int_pow == 0){
console.log("Не поддерживается");
return;
} else if (int_pow != 1){
let list_to_do = map_todo(int_pow);
for (let i = 0; i < list_to_do.length; i++){
dict_interm_probability[list_to_do[i][2]] = multiply_cins_orig(dict_interm_probability[list_to_do[i][0]], dict_interm_probability[list_to_do[i][1]]);
}
}
return dict_interm_probability[int_pow];
}
// Как добраться до интересующего значения, используя x2/+nx для степеней
function map_todo(int_wanted){
// На примере int_wanted = 5
// Степени "числа":
// 1
// 1 * 2 = 2 -> Array(1, 1, 2)
// 2 * 2 = 4 -> Array(2, 2, 4)
// 4 + 1 = 5 -> Array(4, 1, 5)
let int_current_id = 1;
let int_sum = 1;
let b_ascending = true;
let list_solution = new Array();
let i = 0;
while (true){
if (int_sum == int_wanted){
break;
} else if (b_ascending && 2 * int_current_id <= int_wanted){
list_solution[i] = [int_current_id, int_current_id, 2 * int_current_id]; // mult_1, mult_2, result
i++;
int_current_id = 2 * int_current_id;
int_sum = int_current_id;
} else if (b_ascending && 2 * int_current_id > int_wanted){
b_ascending = false;
int_sum = int_current_id;
int_current_id = Math.ceil(int_current_id / 2); // чтобы возвращал именно integer
} else if (!b_ascending && int_sum + int_current_id <= int_wanted){
list_solution[i] = [int_sum, int_current_id, int_sum + int_current_id]; // mult_1, mult_2, result
i++;
int_sum = int_sum + int_current_id;
int_current_id = Math.ceil(int_current_id / 2); // чтобы возвращал именно integer
} else if (!b_ascending && int_sum + int_current_id > int_wanted){
int_current_id = Math.ceil(int_current_id / 2); // чтобы возвращал именно integer
}
}
return list_solution;
}
// "умножение" в столбик двух массивов/списков
function multiply_cins_orig(list_in_1, list_in_2){
let int_len_1 = list_in_1.length;
let int_len_2 = list_in_2.length;
let list_dummy = new Array();
for (let j = 0; j < int_len_2; j++){
list_dummy[j] = Array(j).fill(0); // [], [0], [0, 0], [0, 0, 0] ...
}
let list_for_sum = new Array();
for (let j = 0; j < int_len_2; j++){
let list_interm = new Array();
for (let i = 0; i < int_len_1; i++){
list_interm[i] = list_in_1[i] * list_in_2[j]
}
list_for_sum[j] = list_dummy[j].concat(list_interm, list_dummy[int_len_2 - j - 1]);
}
// [list_in_1 X elem_2[0], 0, 0, 0, 0, 0]
// [0, list_in_1 X elem_2[1], 0, 0, 0, 0]
// [0, 0, list_in_1 X elem_2[2], 0, 0, 0]
// [0, 0, 0, list_in_1 X elem_2[3], 0, 0]
// [0, 0, 0, 0, list_in_1 X elem_2[4], 0]
// [0, 0, 0, 0, 0, list_in_1 X elem_2[5]]
let list_out = new Array();
for (let i = 0; i < list_for_sum[0].length; i++){
let sum_out = 0;
for (let j = 0; j < int_len_2; j++){
sum_out += list_for_sum[j][i];
}
list_out[i] = sum_out;
}
// [1, 3, 6, 10, 15, 21, 25, 27, 27, 25, 21, 15, 10, 6, 3, 1]
return list_out;
}
main();VBS
Option Explicit
Sub main()
Const c_int_side_dice = 6 'сколько граней у кубика
Const c_int_dice_number = 100 'кол-во кубиков
Const c_int_number_to_find = 200 'число, вероятность выпадения которого хотим найти
Dim probability
probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
MsgBox probability
End Sub
' собственно поиск вероятности определённого значения
Function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice)
If int_number_to_find >= int_dice_number And int_number_to_find <= c_int_side_dice * int_dice_number Then
ReDim list_values(int_dice_number * (c_int_side_dice - 1))
Dim i, j
i = 0
For j = int_dice_number To c_int_side_dice * int_dice_number
list_values(i) = j
i = i + 1
Next
Dim list_interm_probability()
interm_probabilities c_int_side_dice, int_dice_number, list_interm_probability
For i = 0 To int_dice_number * (c_int_side_dice - 1)
If list_values(i) = int_number_to_find Then
Exit For
End If
Next
dice_probability = list_interm_probability(i) / (c_int_side_dice ^ int_dice_number)
Else
'задаваемое число выходит за рамки реально возможного диапазона значений
dice_probability = 0.0
End If
End Function
'возвращает список/массив: сколько раз встречается значение
Sub interm_probabilities(int_side_dice, int_pow, list_out)
'На примере int_side_dice = 6, int_pow = 5
'{
' 1: [1, 1, 1, 1, 1, 1],
' 2: [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1],
' 4: [1, 4, 10, 20, 35, 56, 80, 104, 125, 140, 146, 140, 125, 104, 80, 56, 35, 20, 10, 4, 1]
' 5: [1, 5, 15, 35, 70, 126, 205, 305, 420, 540, 651, 735, 780, 780, 735, 651, 540, 420, 305, 205, 126, 70, 35, 15, 5, 1]
'}
Dim j
Dim list_interm_probability()
ReDim list_interm_probability(int_side_dice - 1)
For j = 0 To int_side_dice - 1
list_interm_probability(j) = 1
Next
Dim dict_interm_probability
Set dict_interm_probability = CreateObject("Scripting.Dictionary")
dict_interm_probability.Add 1, list_interm_probability
If int_pow = 0 Then
MsgBox "Не поддерживается"
Quit
ElseIf int_pow <> 1 Then
Dim list_to_do()
map_todo list_to_do, int_pow
For j = 0 To UBound(list_to_do, 2)
'MsgBox list_to_do(0, j) & vbTab & list_to_do(1, j) & vbTab & list_to_do(2, j)
multiply_cins_orig _
dict_interm_probability.Item(list_to_do(0, j)), _
dict_interm_probability.Item(list_to_do(1, j)), _
list_out
dict_interm_probability.Add list_to_do(2, j), list_out
' ArrOut_1 list_out
Next
End If
End Sub
'Как добраться до интересующего значения, используя x2/+nx для степеней
Sub map_todo(list_solution, int_wanted)
'На примере int_wanted = 5
'Степени "числа":
'1
'1 * 2 = 2 -> Array(1, 1, 2)
'2 * 2 = 4 -> Array(2, 2, 4)
'4 + 1 = 5 -> Array(4, 1, 5)
Dim int_current_id
Dim int_sum
Dim b_ascending
Dim i
int_current_id = 1
int_sum = 1
b_ascending = True
i = -1
Do
If b_ascending And 2 * int_current_id <= int_wanted Then
i = i + 1
ReDim Preserve list_solution(2, i)
list_solution(0, i) = int_current_id
list_solution(1, i) = int_current_id
list_solution(2, i) = 2 * int_current_id
int_current_id = 2 * int_current_id
int_sum = int_current_id
ElseIf b_ascending And 2 * int_current_id > int_wanted Then
b_ascending = False
int_sum = int_current_id
int_current_id = CInt(int_current_id / 2) 'чтобы возвращал именно integer
ElseIf Not b_ascending And int_sum + int_current_id <= int_wanted Then
i = i + 1
ReDim Preserve list_solution(2, i)
list_solution(0, i) = int_sum
list_solution(1, i) = int_current_id
list_solution(2, i) = int_sum + int_current_id
int_sum = int_sum + int_current_id
int_current_id = CInt(int_current_id / 2) 'чтобы возвращал именно integer
ElseIf Not b_ascending And int_sum + int_current_id > int_wanted Then
int_current_id = CInt(int_current_id / 2) 'чтобы возвращал именно integer
End If
Loop Until (int_sum = int_wanted)
End Sub
' "умножение" в столбик двух массивов/списков
Sub multiply_cins_orig(list_in_1, list_in_2, list_in)
Dim int_len_1
Dim int_len_2
int_len_1 = Ubound(list_in_1, 1)
int_len_2 = Ubound(list_in_2, 1)
Dim list_for_sum()
ReDim list_for_sum(int_len_2, int_len_1 + int_len_2)
Dim i, j, k, n
For i = 0 To int_len_2
j = 0
For n = 0 To int_len_2
If i = n Then
For k = 0 To int_len_1
list_for_sum(i, j) = list_in_1(k) * list_in_2(n)
j = j + 1
Next
Else
list_for_sum(i, j) = 0
j = j + 1
End If
Next
Next
'[list_in_1 X elem_2[0], 0, 0, 0, 0, 0]
'[0, list_in_1 X elem_2[1], 0, 0, 0, 0]
'[0, 0, list_in_1 X elem_2[2], 0, 0, 0]
'[0, 0, 0, list_in_1 X elem_2[3], 0, 0]
'[0, 0, 0, 0, list_in_1 X elem_2[4], 0]
'[0, 0, 0, 0, 0, list_in_1 X elem_2[5]]
'ArrOut_2 list_for_sum
Erase list_in
ReDim list_in(int_len_1 + int_len_2)
Dim sum_out
For j = 0 To int_len_1 + int_len_2
sum_out = 0
For i = 0 To int_len_2
sum_out = sum_out + list_for_sum(i, j)
Next
list_in(j) = sum_out
Next
' [1, 3, 6, 10, 15, 21, 25, 27, 27, 25, 21, 15, 10, 6, 3, 1]
'ArrOut_1 list_in
End Sub
'==================================================
'<Additional_MsgBox_For_Arrays>
Sub ArrOut_1(arr_in)
Dim str_out
Dim i
For i = 0 To UBound(arr_in)
If i = 0 Then
str_out = arr_in(i)
Else
str_out = str_out & " " & arr_in(i)
End If
Next
MsgBox str_out
End Sub
Sub ArrOut_2(arr_in)
Dim str_out
Dim i, j
For i = 0 To UBound(arr_in, 1)
For j = 0 To UBound(arr_in, 2)
If i = 0 And j = 0 Then
str_out = arr_in(i, j)
ElseIf j = 0 Then
str_out = str_out & vbNewLine & arr_in(i, j)
Else
str_out = str_out & " " & arr_in(i, j)
End If
Next
Next
MsgBox str_out
End Sub
'</Additional_MsgBox_For_Arrays>
'==================================================
mainВизуализация алгоритма, II попытка
Если быть достаточно честным, то из 3-х выложенных скриптов именно до 1000-го кубика может добраться только Python (без использования библиотеки numpy), а JavaScript и VBS выпадают в ошибку переполнение переменной. Предлагаю сделать небольшую хитрость: считать сразу вероятность выпадения внутри операции свёртки последовательностей / "умножения в столбик", вместо только делимого. Т.е. на вход сразу подавать последовательность [1/6 1/6 1/6 1/6 1/6 1/6] вместо [1 1 1 1 1 1] и, следовательно, на выходе всех операций свёртки последовательностей / "умножения в столбик" мы получим последовательность / массив / список вероятностей.
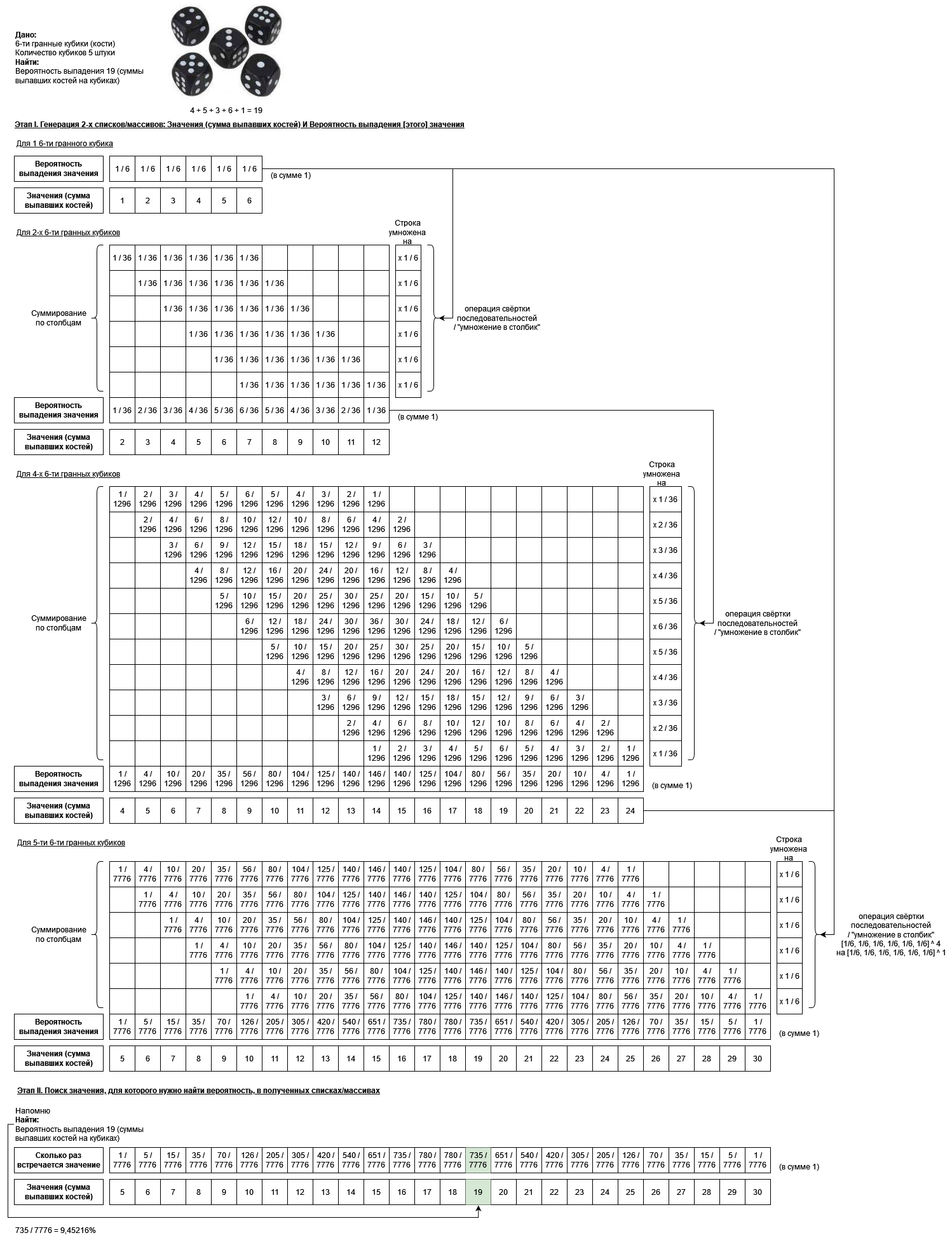
Python. Пример. Свёртка последовательностей [1/6 1/6 1/6 1/6 1/6 1/6]
Понимаю, что дроби проверять - дело не благодарное, следовательно добавляю степень 6 ** n * ... - делитель вероятности. Это сделано чисто для упрощения проверки.
# -*- coding: utf-8 -*-
import numpy
convolve_out = numpy.convolve([1 / 6] * 6, [1 / 6] * 6)
# [1 2 3 4 5 6 5 4 3 2 1]
print(6 ** 2 * convolve_out)
convolve_out = numpy.convolve(convolve_out, convolve_out)
# [ 1 4 10 20 35 56 80 104 125 140 146 140 125 104 80 56 35 20 10 4 1]
print(6 ** 4 * convolve_out )
convolve_out = numpy.convolve(convolve_out, [1 / 6] * 6)
# [ 1 5 15 35 70 126 205 305 420 540 651 735 780 780 735 651 540 420 305 205 126 70 35 15 5 1]
print(6 ** 5 * convolve_out)
Скрипты, II попытка
До 1000-го кубика добираются все. Простор для оптимизаций оставляю читателям.
Python
# -*- coding: utf-8 -*-
# import numpy # <можно_использовать_numpy>
def main():
c_int_side_dice: int = 6 # сколько граней у кубика
c_int_dice_number: int = 1000 # кол-во кубиков
c_int_number_to_find: int = 2000 # число, вероятность выпадения которого хотим найти
probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
print(probability)
# собственно поиск вероятности определённого значения
def dice_probability(int_dice_number: int, int_number_to_find: int, c_int_side_dice: int) -> float:
if int_number_to_find >= int_dice_number and int_number_to_find <= c_int_side_dice * int_dice_number:
list_values: list[int] = [i for i in range(int_dice_number, c_int_side_dice * int_dice_number + 1)]
list_probability = get_probabilities(c_int_side_dice, int_dice_number)
for i in range(len(list_values)):
if list_values[i] == int_number_to_find:
float_out: float = list_probability[i]
break
return float_out
else:
# задаваемое число выходит за рамки реально возможного диапазона значений
return 0.0
# возвращает список/массив: вероятности выадения
def get_probabilities(int_side_dice: int, int_pow: int) -> list[float]:
"""
На примере int_side_dice = 6, int_pow = 5
{
1: [1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6],
2: [1 / 36, 2 / 36, 3 / 36, 4 / 36, 5 / 36, 6 / 36, 5 / 36, 4 / 36, 3 / 36, 2 / 36, 1 / 36],
4: [1 / 1296, 4 / 1296, 10 / 1296, 20 / 1296, 35 / 1296, 56 / 1296, 80 / 1296, 104 / 1296, 125 / 1296, 140 / 1296, 146 / 1296, 140 / 1296, 125 / 1296, 104 / 1296, 80 / 1296, 56 / 1296, 35 / 1296, 20 / 1296, 10 / 1296, 4 / 1296, 1 / 1296]
5: [1 / 7776, 5 / 7776, 15 / 7776, 35 / 7776, 70 / 7776, 126 / 7776, 205 / 7776, 305 / 7776, 420 / 7776, 540 / 7776, 651 / 7776, 735 / 7776, 780 / 7776, 780 / 7776, 735 / 7776, 651 / 7776, 540 / 7776, 420 / 7776, 305 / 7776, 205 / 7776, 126 / 7776, 70 / 7776, 35 / 7776, 15 / 7776, 5 / 7776, 1 / 7776]
}
"""
dict_interm_probability = {1: [1 / int_side_dice] * int_side_dice}
if int_pow == 0:
print("Не поддерживается")
quit()
elif int_pow != 1:
list_to_do = map_todo(int_pow)
for elem in list_to_do:
dict_interm_probability[elem[2]] = multiply_cins_orig(dict_interm_probability[elem[0]], dict_interm_probability[elem[1]])
# dict_interm_probability[elem[2]] = numpy.convolve(dict_interm_probability[elem[0]], dict_interm_probability[elem[1]]) # <можно_использовать_numpy> и не использовать multiply_cins_orig()
return dict_interm_probability[int_pow]
# Как добраться до интересующего значения, используя x2/+nx для степеней
def map_todo(int_wanted: int) -> list[tuple[int, int, int]]:
"""
На примере int_wanted = 5
Степени "числа":
1
1 * 2 = 2 -> tuple(1, 1, 2)
2 * 2 = 4 -> tuple(2, 2, 4)
4 + 1 = 5 -> tuple(4, 1, 5)
"""
int_current_id: int = 1
int_sum: int = 1
b_ascending: bool = True
list_solution: list[tuple[int, int, int]] = []
while True:
if int_sum == int_wanted:
break
elif b_ascending and 2 * int_current_id <= int_wanted:
list_solution.append( # mult_1, mult_2, result
(int_current_id, int_current_id, 2 * int_current_id)
)
int_current_id = 2 * int_current_id
int_sum = int_current_id
elif b_ascending and 2 * int_current_id > int_wanted:
b_ascending = False
int_sum = int_current_id
int_current_id = int(int_current_id / 2) # чтобы возвращал именно integer
elif not b_ascending and int_sum + int_current_id <= int_wanted:
list_solution.append( # mult_1, mult_2, result
(int_sum, int_current_id, int_sum + int_current_id)
)
int_sum = int_sum + int_current_id
int_current_id = int(int_current_id / 2) # чтобы возвращал именно integer
elif not b_ascending and int_sum + int_current_id > int_wanted:
int_current_id = int(int_current_id / 2) # чтобы возвращал именно integer
return list_solution
# "умножение" в столбик двух массивов/списков
def multiply_cins_orig(list_in_1: list[int], list_in_2: list[int]) -> list[int]:
int_len_2: int = len(list_in_2)
list_dummy: list[list[int]] = []
for i in range(int_len_2):
list_dummy.append([0] * i) # [], [0], [0, 0], [0, 0, 0] ...
list_for_sum: list[list[int]] = []
i: int = -1
for elem_2 in list_in_2:
i += 1
list_interm: list[int] = [elem_1 * elem_2 for elem_1 in list_in_1]
list_for_sum.append(list_dummy[i] + list_interm + list_dummy[int_len_2 - i - 1])
"""
[list_in_1 X list_in_2[0], 0, 0, 0, 0, 0]
[0, list_in_1 X list_in_2[1], 0, 0, 0, 0]
[0, 0, list_in_1 X list_in_2[2], 0, 0, 0]
[0, 0, 0, list_in_1 X list_in_2[3], 0, 0]
[0, 0, 0, 0, list_in_1 X list_in_2[4], 0]
[0, 0, 0, 0, 0, list_in_1 X list_in_2[5]]
"""
list_out: list[int] = []
for i in range(len(list_for_sum[0])):
sum_out: int = 0
for j in range(int_len_2):
sum_out += list_for_sum[j][i]
list_out.append(sum_out)
"""
[1 / 216, 3 / 216, 6 / 216, 10 / 216, 15 / 216, 21 / 216, 25 / 216, 27 / 216, 27 / 216, 25 / 216, 21 / 216, 15 / 216, 10 / 216, 6 / 216, 3 / 216, 1 / 216]
"""
return list_out
main()
JavaScript
function main(){
const c_int_side_dice = 6; // сколько граней у кубика
const c_int_dice_number = 1000; // кол-во кубиков
const c_int_number_to_find = 2000; // число, вероятность выпадения которого хотим найти
let probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice);
console.log(probability);
}
// собственно поиск вероятности определённого значения
function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice){
if (int_number_to_find >= int_dice_number && int_number_to_find <= c_int_side_dice * int_dice_number){
let list_values = new Array();
let i = 0;
for (let j = int_dice_number; j <= c_int_side_dice * int_dice_number; j++){
list_values[i] = j;
i++;
}
let list_probability = get_probabilities(c_int_side_dice, int_dice_number);
let float_out;
for (let i = 0; i <= list_values.length; i++){
if (list_values[i] == int_number_to_find){
float_out = list_probability[i];
break;
}
}
return float_out;
} else {
// задаваемое число выходит за рамки реально возможного диапазона значений
return 0.0;
}
}
// возвращает список/массив: вероятности выадения
function get_probabilities(int_side_dice, int_pow){
// На примере int_side_dice = 6, int_pow = 5
// {
// 1: [1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6],
// 2: [1 / 36, 2 / 36, 3 / 36, 4 / 36, 5 / 36, 6 / 36, 5 / 36, 4 / 36, 3 / 36, 2 / 36, 1 / 36],
// 4: [1 / 1296, 4 / 1296, 10 / 1296, 20 / 1296, 35 / 1296, 56 / 1296, 80 / 1296, 104 / 1296, 125 / 1296, 140 / 1296, 146 / 1296, 140 / 1296, 125 / 1296, 104 / 1296, 80 / 1296, 56 / 1296, 35 / 1296, 20 / 1296, 10 / 1296, 4 / 1296, 1 / 1296]
// 5: [1 / 7776, 5 / 7776, 15 / 7776, 35 / 7776, 70 / 7776, 126 / 7776, 205 / 7776, 305 / 7776, 420 / 7776, 540 / 7776, 651 / 7776, 735 / 7776, 780 / 7776, 780 / 7776, 735 / 7776, 651 / 7776, 540 / 7776, 420 / 7776, 305 / 7776, 205 / 7776, 126 / 7776, 70 / 7776, 35 / 7776, 15 / 7776, 5 / 7776, 1 / 7776]
// }
let dict_interm_probability = {1: Array(int_side_dice).fill(1 / int_side_dice)};
if (int_pow == 0){
console.log("Не поддерживается");
return;
} else if (int_pow != 1){
let list_to_do = map_todo(int_pow);
for (let i = 0; i < list_to_do.length; i++){
dict_interm_probability[list_to_do[i][2]] = multiply_cins_orig(dict_interm_probability[list_to_do[i][0]], dict_interm_probability[list_to_do[i][1]]);
}
}
return dict_interm_probability[int_pow];
}
// Как добраться до интересующего значения, используя x2/+nx для степеней
function map_todo(int_wanted){
// На примере int_wanted = 5
// Степени "числа":
// 1
// 1 * 2 = 2 -> Array(1, 1, 2)
// 2 * 2 = 4 -> Array(2, 2, 4)
// 4 + 1 = 5 -> Array(4, 1, 5)
let int_current_id = 1;
let int_sum = 1;
let b_ascending = true;
let list_solution = new Array();
let i = 0;
while (true){
if (int_sum == int_wanted){
break;
} else if (b_ascending && 2 * int_current_id <= int_wanted){
list_solution[i] = [int_current_id, int_current_id, 2 * int_current_id]; // mult_1, mult_2, result
i++;
int_current_id = 2 * int_current_id;
int_sum = int_current_id;
} else if (b_ascending && 2 * int_current_id > int_wanted){
b_ascending = false;
int_sum = int_current_id;
int_current_id = Math.ceil(int_current_id / 2); // чтобы возвращал именно integer
} else if (!b_ascending && int_sum + int_current_id <= int_wanted){
list_solution[i] = [int_sum, int_current_id, int_sum + int_current_id]; // mult_1, mult_2, result
i++;
int_sum = int_sum + int_current_id;
int_current_id = Math.ceil(int_current_id / 2); // чтобы возвращал именно integer
} else if (!b_ascending && int_sum + int_current_id > int_wanted){
int_current_id = Math.ceil(int_current_id / 2); // чтобы возвращал именно integer
}
}
return list_solution;
}
// "умножение" в столбик двух массивов/списков
function multiply_cins_orig(list_in_1, list_in_2){
let int_len_1 = list_in_1.length;
let int_len_2 = list_in_2.length;
let list_dummy = new Array();
for (let j = 0; j < int_len_2; j++){
list_dummy[j] = Array(j).fill(0); // [], [0], [0, 0], [0, 0, 0] ...
}
let list_for_sum = new Array();
for (let j = 0; j < int_len_2; j++){
let list_interm = new Array();
for (let i = 0; i < int_len_1; i++){
list_interm[i] = list_in_1[i] * list_in_2[j]
}
list_for_sum[j] = list_dummy[j].concat(list_interm, list_dummy[int_len_2 - j - 1]);
}
// [list_in_1 X list_in_2[0], 0, 0, 0, 0, 0]
// [0, list_in_1 X list_in_2[1], 0, 0, 0, 0]
// [0, 0, list_in_1 X list_in_2[2], 0, 0, 0]
// [0, 0, 0, list_in_1 X list_in_2[3], 0, 0]
// [0, 0, 0, 0, list_in_1 X list_in_2[4], 0]
// [0, 0, 0, 0, 0, list_in_1 X list_in_2[5]]
let list_out = new Array();
for (let i = 0; i < list_for_sum[0].length; i++){
let sum_out = 0;
for (let j = 0; j < int_len_2; j++){
sum_out += list_for_sum[j][i];
}
list_out[i] = sum_out;
}
// [1 / 216, 3 / 216, 6 / 216, 10 / 216, 15 / 216, 21 / 216, 25 / 216, 27 / 216, 27 / 216, 25 / 216, 21 / 216, 15 / 216, 10 / 216, 6 / 216, 3 / 216, 1 / 216]
return list_out;
}
main();VBS
Option Explicit
Sub main()
Const c_int_side_dice = 6 'сколько граней у кубика
Const c_int_dice_number = 1000 'кол-во кубиков
Const c_int_number_to_find = 2000 'число, вероятность выпадения которого хотим найти
Dim probability
probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
MsgBox probability
End Sub
' собственно поиск вероятности определённого значения
Function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice)
If int_number_to_find >= int_dice_number And int_number_to_find <= c_int_side_dice * int_dice_number Then
ReDim list_values(int_dice_number * (c_int_side_dice - 1))
Dim i, j
i = 0
For j = int_dice_number To c_int_side_dice * int_dice_number
list_values(i) = j
i = i + 1
Next
Dim list_probability()
get_probabilities c_int_side_dice, int_dice_number, list_probability
For i = 0 To int_dice_number * (c_int_side_dice - 1)
If list_values(i) = int_number_to_find Then
Exit For
End If
Next
dice_probability = list_probability(i)
Else
'задаваемое число выходит за рамки реально возможного диапазона значений
dice_probability = 0.0
End If
End Function
'возвращает список/массив: вероятности выадения
Sub get_probabilities(int_side_dice, int_pow, list_out)
'На примере int_side_dice = 6, int_pow = 5
'{
' 1: [1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6],
' 2: [1 / 36, 2 / 36, 3 / 36, 4 / 36, 5 / 36, 6 / 36, 5 / 36, 4 / 36, 3 / 36, 2 / 36, 1 / 36],
' 4: [1 / 1296, 4 / 1296, 10 / 1296, 20 / 1296, 35 / 1296, 56 / 1296, 80 / 1296, 104 / 1296, 125 / 1296, 140 / 1296, 146 / 1296, 140 / 1296, 125 / 1296, 104 / 1296, 80 / 1296, 56 / 1296, 35 / 1296, 20 / 1296, 10 / 1296, 4 / 1296, 1 / 1296]
' 5: [1 / 7776, 5 / 7776, 15 / 7776, 35 / 7776, 70 / 7776, 126 / 7776, 205 / 7776, 305 / 7776, 420 / 7776, 540 / 7776, 651 / 7776, 735 / 7776, 780 / 7776, 780 / 7776, 735 / 7776, 651 / 7776, 540 / 7776, 420 / 7776, 305 / 7776, 205 / 7776, 126 / 7776, 70 / 7776, 35 / 7776, 15 / 7776, 5 / 7776, 1 / 7776]
'}
Dim j
Dim list_probability()
ReDim list_probability(int_side_dice - 1)
For j = 0 To int_side_dice - 1
list_probability(j) = 1 / int_side_dice
Next
Dim dict_interm_probability
Set dict_interm_probability = CreateObject("Scripting.Dictionary")
dict_interm_probability.Add 1, list_probability
If int_pow = 0 Then
MsgBox "Не поддерживается"
Quit
ElseIf int_pow <> 1 Then
Dim list_to_do()
map_todo list_to_do, int_pow
For j = 0 To UBound(list_to_do, 2)
'MsgBox list_to_do(0, j) & vbTab & list_to_do(1, j) & vbTab & list_to_do(2, j)
multiply_cins_orig _
dict_interm_probability.Item(list_to_do(0, j)), _
dict_interm_probability.Item(list_to_do(1, j)), _
list_out
dict_interm_probability.Add list_to_do(2, j), list_out
' ArrOut_1 list_out
Next
End If
End Sub
'Как добраться до интересующего значения, используя x2/+nx для степеней
Sub map_todo(list_solution, int_wanted)
'На примере int_wanted = 5
'Степени "числа":
'1
'1 * 2 = 2 -> Array(1, 1, 2)
'2 * 2 = 4 -> Array(2, 2, 4)
'4 + 1 = 5 -> Array(4, 1, 5)
Dim int_current_id
Dim int_sum
Dim b_ascending
Dim i
int_current_id = 1
int_sum = 1
b_ascending = True
i = -1
Do
If b_ascending And 2 * int_current_id <= int_wanted Then
i = i + 1
ReDim Preserve list_solution(2, i)
list_solution(0, i) = int_current_id
list_solution(1, i) = int_current_id
list_solution(2, i) = 2 * int_current_id
int_current_id = 2 * int_current_id
int_sum = int_current_id
ElseIf b_ascending And 2 * int_current_id > int_wanted Then
b_ascending = False
int_sum = int_current_id
int_current_id = CInt(int_current_id / 2) 'чтобы возвращал именно integer
ElseIf Not b_ascending And int_sum + int_current_id <= int_wanted Then
i = i + 1
ReDim Preserve list_solution(2, i)
list_solution(0, i) = int_sum
list_solution(1, i) = int_current_id
list_solution(2, i) = int_sum + int_current_id
int_sum = int_sum + int_current_id
int_current_id = CInt(int_current_id / 2) 'чтобы возвращал именно integer
ElseIf Not b_ascending And int_sum + int_current_id > int_wanted Then
int_current_id = CInt(int_current_id / 2) 'чтобы возвращал именно integer
End If
Loop Until (int_sum = int_wanted)
End Sub
' "умножение" в столбик двух массивов/списков
Sub multiply_cins_orig(list_in_1, list_in_2, list_in)
Dim int_len_1
Dim int_len_2
int_len_1 = Ubound(list_in_1, 1)
int_len_2 = Ubound(list_in_2, 1)
Dim list_for_sum()
ReDim list_for_sum(int_len_2, int_len_1 + int_len_2)
Dim i, j, k, n
For i = 0 To int_len_2
j = 0
For n = 0 To int_len_2
If i = n Then
For k = 0 To int_len_1
list_for_sum(i, j) = list_in_1(k) * list_in_2(n)
j = j + 1
Next
Else
list_for_sum(i, j) = 0
j = j + 1
End If
Next
Next
'[list_in_1 X list_in_2[0], 0, 0, 0, 0, 0]
'[0, list_in_1 X list_in_2[1], 0, 0, 0, 0]
'[0, 0, list_in_1 X list_in_2[2], 0, 0, 0]
'[0, 0, 0, list_in_1 X list_in_2[3], 0, 0]
'[0, 0, 0, 0, list_in_1 X list_in_2[4], 0]
'[0, 0, 0, 0, 0, list_in_1 X list_in_2[5]]
'ArrOut_2 list_for_sum
Erase list_in
ReDim list_in(int_len_1 + int_len_2)
Dim sum_out
For j = 0 To int_len_1 + int_len_2
sum_out = 0
For i = 0 To int_len_2
sum_out = sum_out + list_for_sum(i, j)
Next
list_in(j) = sum_out
Next
' [1 / 216, 3 / 216, 6 / 216, 10 / 216, 15 / 216, 21 / 216, 25 / 216, 27 / 216, 27 / 216, 25 / 216, 21 / 216, 15 / 216, 10 / 216, 6 / 216, 3 / 216, 1 / 216]
'ArrOut_1 list_in
End Sub
'==================================================
'<Additional_MsgBox_For_Arrays>
Sub ArrOut_1(arr_in)
Dim str_out
Dim i
For i = 0 To UBound(arr_in)
If i = 0 Then
str_out = arr_in(i)
Else
str_out = str_out & " " & arr_in(i)
End If
Next
MsgBox str_out
End Sub
Sub ArrOut_2(arr_in)
Dim str_out
Dim i, j
For i = 0 To UBound(arr_in, 1)
For j = 0 To UBound(arr_in, 2)
If i = 0 And j = 0 Then
str_out = arr_in(i, j)
ElseIf j = 0 Then
str_out = str_out & vbNewLine & arr_in(i, j)
Else
str_out = str_out & " " & arr_in(i, j)
End If
Next
Next
MsgBox str_out
End Sub
'</Additional_MsgBox_For_Arrays>
'==================================================
mainПару слов о проверке
Проверку и перепроверку чьих бы то ни было слов всегда приветствую.
Однако, отмечу, что на текущий момент кроме как эмпирического (т.е. обычного сравнения результата работы описанного в текущей статье алгоритма с работой алгоритма в предыдущей статье или обычного расчёта “в лоб”) метода проверки я не располагаю каким-либо иным доказательством своей правоты, которое бы сочетало как доступность восприятия так и наглядность.
Следовательно:
Если Вы достаточно доверяете предыдущей статье — то можно сверять результат работы алгоритма в текущей статье с алгоритмом, описанным в предыдущей статье.
Если не доверяете предыдущей статье, тогда могу предложить следующее: генератор SQL запросов, считающих в лоб кубики, суммы их выпадений и их вероятности.
Python для проверок в лоб
# -*- coding: utf-8 -*-
import sqlite3
import re
def main() -> None:
c_int_side_dice: int = 6 # сколько граней у кубика
c_int_dice_number: int = 6 # кол-во кубиков
str_query = select_values_and_interm_probabilities(c_int_side_dice, c_int_dice_number)
if True:
# Просмотр SQL кода
print(str_query)
else:
# Прогон SQL запроса
conn = sqlite3.connect(":memory:")
cursor = conn.cursor()
cursor.execute(str_query)
return_select(cursor)
cursor.close()
conn.close()
def select_values_and_interm_probabilities(int_side_dice: int, int_dice_number: int) -> str:
str_sub_query_1: str = """
-- заводим значения сторон кубика
WITH RECURSIVE step_01_insert (dice) AS (
SELECT 1 AS dice
UNION ALL
SELECT dice + 1 AS dice
FROM step_01_insert
WHERE dice < {} -- сколько граней у кубика
)
""".format(int_side_dice)
list_sub_query_1: list[str] = []
list_sub_query_2: list[str] = []
list_sub_query_3: list[str] = []
for i in range(int_dice_number):
list_sub_query_1.append("T{}.dice AS dice_{}".format(i, i))
list_sub_query_2.append("T{}.dice".format(i))
list_sub_query_3.append("step_01_insert AS T{}".format(i))
str_sub_query_2: str = "\n".join([
"-- генерируем все возможные ситуации для {}-х кубиков".format(int_dice_number),
", step_02_spawn AS (",
"SELECT",
"\n, ".join(list_sub_query_1),
", " + " + ".join(list_sub_query_2) + " AS dice_sum -- Значения (сумма выпавших костей)",
"FROM",
"\n, ".join(list_sub_query_3),
")"
])
del list_sub_query_1, list_sub_query_2, list_sub_query_3
str_sub_query_3: str = """
-- считаем в лоб, сколько раз встречается значение
, step_03_dividend (dice_sum, dividend) AS (
SELECT dice_sum -- Значения (сумма выпавших костей)
, COUNT(1) AS dividend -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
)
, step_04_divisor(divisor) AS (
SELECT SUM(dividend) AS divisor
FROM step_03_dividend
)
SELECT T1.dice_sum -- Значения (сумма выпавших костей)
, T1.dividend -- Сколько раз встречается значение
, CAST(T1.dividend AS REAL) / CAST(T2.divisor AS REAL) AS probability -- Вероятность
FROM step_03_dividend AS T1
, step_04_divisor AS T2
ORDER BY T1.dice_sum;
"""
return lazy_prety_print(str_sub_query_1 + str_sub_query_2 + str_sub_query_3)
def lazy_prety_print(str_in: str) -> str:
list_line: list[str] = []
str_offset: str = ""
for str_line_1 in str_in.split("\n"):
str_line_2 = re.sub(r"^\s+", "", str_line_1)
if len(str_line_2) > 0 and str_line_2[0] == ")":
str_offset = str_offset[:-4]
list_line.append(str_offset + str_line_2)
if len(str_line_2) > 0 and str_line_2[-1] == "(":
str_offset = str_offset + " "
return "\n".join(list_line)
def return_select(cursor: sqlite3.Cursor) -> None:
column_list = []
for column in cursor.description:
column_list.append(column[0])
print("\t".join(column_list))
rows = cursor.fetchall()
for row in rows:
column_list = []
for row_column in row:
column_list.append(str(row_column))
print("\t".join(column_list))
if __name__ == "__main__":
main()
Результаты работы данного скрипта приведены ниже:
SQL для 3-х кубиков
-- заводим значения сторон кубика
WITH RECURSIVE step_01_insert (dice) AS (
SELECT 1 AS dice
UNION ALL
SELECT dice + 1 AS dice
FROM step_01_insert
WHERE dice < 6 -- сколько граней у кубика
)
-- генерируем все возможные ситуации для 3-х кубиков
, step_02_spawn AS (
SELECT
T0.dice AS dice_0
, T1.dice AS dice_1
, T2.dice AS dice_2
, T0.dice + T1.dice + T2.dice AS dice_sum -- Значения (сумма выпавших костей)
FROM
step_01_insert AS T0
, step_01_insert AS T1
, step_01_insert AS T2
)
-- считаем в лоб, сколько раз встречается значение
, step_03_dividend (dice_sum, dividend) AS (
SELECT dice_sum -- Значения (сумма выпавших костей)
, COUNT(1) AS dividend -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
)
, step_04_divisor(divisor) AS (
SELECT SUM(dividend) AS divisor
FROM step_03_dividend
)
SELECT T1.dice_sum -- Значения (сумма выпавших костей)
, T1.dividend -- Сколько раз встречается значение
, CAST(T1.dividend AS REAL) / CAST(T2.divisor AS REAL) AS probability -- Вероятность
FROM step_03_dividend AS T1
, step_04_divisor AS T2
ORDER BY T1.dice_sum;dice_sum | dividend | probability |
3 | 1 | 0.004629629629629629 |
4 | 3 | 0.013888888888888888 |
5 | 6 | 0.027777777777777776 |
6 | 10 | 0.046296296296296294 |
7 | 15 | 0.06944444444444445 |
8 | 21 | 0.09722222222222222 |
9 | 25 | 0.11574074074074074 |
10 | 27 | 0.125 |
11 | 27 | 0.125 |
12 | 25 | 0.11574074074074074 |
13 | 21 | 0.09722222222222222 |
14 | 15 | 0.06944444444444445 |
15 | 10 | 0.046296296296296294 |
16 | 6 | 0.027777777777777776 |
17 | 3 | 0.013888888888888888 |
18 | 1 | 0.004629629629629629 |
SQL для 4-х кубиков
-- заводим значения сторон кубика
WITH RECURSIVE step_01_insert (dice) AS (
SELECT 1 AS dice
UNION ALL
SELECT dice + 1 AS dice
FROM step_01_insert
WHERE dice < 6 -- сколько граней у кубика
)
-- генерируем все возможные ситуации для 4-х кубиков
, step_02_spawn AS (
SELECT
T0.dice AS dice_0
, T1.dice AS dice_1
, T2.dice AS dice_2
, T3.dice AS dice_3
, T0.dice + T1.dice + T2.dice + T3.dice AS dice_sum -- Значения (сумма выпавших костей)
FROM
step_01_insert AS T0
, step_01_insert AS T1
, step_01_insert AS T2
, step_01_insert AS T3
)
-- считаем в лоб, сколько раз встречается значение
, step_03_dividend (dice_sum, dividend) AS (
SELECT dice_sum -- Значения (сумма выпавших костей)
, COUNT(1) AS dividend -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
)
, step_04_divisor(divisor) AS (
SELECT SUM(dividend) AS divisor
FROM step_03_dividend
)
SELECT T1.dice_sum -- Значения (сумма выпавших костей)
, T1.dividend -- Сколько раз встречается значение
, CAST(T1.dividend AS REAL) / CAST(T2.divisor AS REAL) AS probability -- Вероятность
FROM step_03_dividend AS T1
, step_04_divisor AS T2
ORDER BY T1.dice_sum;dice_sum | dividend | probability |
4 | 1 | 0.0007716049382716049 |
5 | 4 | 0.0030864197530864196 |
6 | 10 | 0.007716049382716049 |
7 | 20 | 0.015432098765432098 |
8 | 35 | 0.02700617283950617 |
9 | 56 | 0.043209876543209874 |
10 | 80 | 0.06172839506172839 |
11 | 104 | 0.08024691358024691 |
12 | 125 | 0.09645061728395062 |
13 | 140 | 0.10802469135802469 |
14 | 146 | 0.11265432098765432 |
15 | 140 | 0.10802469135802469 |
16 | 125 | 0.09645061728395062 |
17 | 104 | 0.08024691358024691 |
18 | 80 | 0.06172839506172839 |
19 | 56 | 0.043209876543209874 |
20 | 35 | 0.02700617283950617 |
21 | 20 | 0.015432098765432098 |
22 | 10 | 0.007716049382716049 |
23 | 4 | 0.0030864197530864196 |
24 | 1 | 0.0007716049382716049 |
SQL для 5-х кубиков
-- заводим значения сторон кубика
WITH RECURSIVE step_01_insert (dice) AS (
SELECT 1 AS dice
UNION ALL
SELECT dice + 1 AS dice
FROM step_01_insert
WHERE dice < 6 -- сколько граней у кубика
)
-- генерируем все возможные ситуации для 5-х кубиков
, step_02_spawn AS (
SELECT
T0.dice AS dice_0
, T1.dice AS dice_1
, T2.dice AS dice_2
, T3.dice AS dice_3
, T4.dice AS dice_4
, T0.dice + T1.dice + T2.dice + T3.dice + T4.dice AS dice_sum -- Значения (сумма выпавших костей)
FROM
step_01_insert AS T0
, step_01_insert AS T1
, step_01_insert AS T2
, step_01_insert AS T3
, step_01_insert AS T4
)
-- считаем в лоб, сколько раз встречается значение
, step_03_dividend (dice_sum, dividend) AS (
SELECT dice_sum -- Значения (сумма выпавших костей)
, COUNT(1) AS dividend -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
)
, step_04_divisor(divisor) AS (
SELECT SUM(dividend) AS divisor
FROM step_03_dividend
)
SELECT T1.dice_sum -- Значения (сумма выпавших костей)
, T1.dividend -- Сколько раз встречается значение
, CAST(T1.dividend AS REAL) / CAST(T2.divisor AS REAL) AS probability -- Вероятность
FROM step_03_dividend AS T1
, step_04_divisor AS T2
ORDER BY T1.dice_sum;dice_sum | dividend | probability |
5 | 1 | 0.0001286008230452675 |
6 | 5 | 0.0006430041152263374 |
7 | 15 | 0.0019290123456790122 |
8 | 35 | 0.0045010288065843625 |
9 | 70 | 0.009002057613168725 |
10 | 126 | 0.016203703703703703 |
11 | 205 | 0.026363168724279837 |
12 | 305 | 0.03922325102880658 |
13 | 420 | 0.05401234567901234 |
14 | 540 | 0.06944444444444445 |
15 | 651 | 0.08371913580246913 |
16 | 735 | 0.09452160493827161 |
17 | 780 | 0.10030864197530864 |
18 | 780 | 0.10030864197530864 |
19 | 735 | 0.09452160493827161 |
20 | 651 | 0.08371913580246913 |
21 | 540 | 0.06944444444444445 |
22 | 420 | 0.05401234567901234 |
23 | 305 | 0.03922325102880658 |
24 | 205 | 0.026363168724279837 |
25 | 126 | 0.016203703703703703 |
26 | 70 | 0.009002057613168725 |
27 | 35 | 0.0045010288065843625 |
28 | 15 | 0.0019290123456790122 |
29 | 5 | 0.0006430041152263374 |
30 | 1 | 0.0001286008230452675 |
SQL для 6-х кубиков
-- заводим значения сторон кубика
WITH RECURSIVE step_01_insert (dice) AS (
SELECT 1 AS dice
UNION ALL
SELECT dice + 1 AS dice
FROM step_01_insert
WHERE dice < 6 -- сколько граней у кубика
)
-- генерируем все возможные ситуации для 6-х кубиков
, step_02_spawn AS (
SELECT
T0.dice AS dice_0
, T1.dice AS dice_1
, T2.dice AS dice_2
, T3.dice AS dice_3
, T4.dice AS dice_4
, T5.dice AS dice_5
, T0.dice + T1.dice + T2.dice + T3.dice + T4.dice + T5.dice AS dice_sum -- Значения (сумма выпавших костей)
FROM
step_01_insert AS T0
, step_01_insert AS T1
, step_01_insert AS T2
, step_01_insert AS T3
, step_01_insert AS T4
, step_01_insert AS T5
)
-- считаем в лоб, сколько раз встречается значение
, step_03_dividend (dice_sum, dividend) AS (
SELECT dice_sum -- Значения (сумма выпавших костей)
, COUNT(1) AS dividend -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
)
, step_04_divisor(divisor) AS (
SELECT SUM(dividend) AS divisor
FROM step_03_dividend
)
SELECT T1.dice_sum -- Значения (сумма выпавших костей)
, T1.dividend -- Сколько раз встречается значение
, CAST(T1.dividend AS REAL) / CAST(T2.divisor AS REAL) AS probability -- Вероятность
FROM step_03_dividend AS T1
, step_04_divisor AS T2
ORDER BY T1.dice_sum;dice_sum | dividend | probability |
6 | 1 | 2.143347050754458e-05 |
7 | 6 | 0.0001286008230452675 |
8 | 21 | 0.0004501028806584362 |
9 | 56 | 0.0012002743484224967 |
10 | 126 | 0.002700617283950617 |
11 | 252 | 0.005401234567901234 |
12 | 456 | 0.00977366255144033 |
13 | 756 | 0.016203703703703703 |
14 | 1161 | 0.02488425925925926 |
15 | 1666 | 0.03570816186556927 |
16 | 2247 | 0.048161008230452676 |
17 | 2856 | 0.061213991769547324 |
18 | 3431 | 0.07353823731138547 |
19 | 3906 | 0.08371913580246913 |
20 | 4221 | 0.09047067901234568 |
21 | 4332 | 0.09284979423868313 |
22 | 4221 | 0.09047067901234568 |
23 | 3906 | 0.08371913580246913 |
24 | 3431 | 0.07353823731138547 |
25 | 2856 | 0.061213991769547324 |
26 | 2247 | 0.048161008230452676 |
27 | 1666 | 0.03570816186556927 |
28 | 1161 | 0.02488425925925926 |
29 | 756 | 0.016203703703703703 |
30 | 456 | 0.00977366255144033 |
31 | 252 | 0.005401234567901234 |
32 | 126 | 0.002700617283950617 |
33 | 56 | 0.0012002743484224967 |
34 | 21 | 0.0004501028806584362 |
35 | 6 | 0.0001286008230452675 |
36 | 1 | 2.143347050754458e-05 |
Выводы
В данной статье мы познакомились:
- с операцией свёртка последовательностей
- как при помощи свёртки последовательностей считать вероятности выпадения кубиков
- как посчитать вероятности выпадения найти вероятность выпадения числа k, а именно суммы всех значений, выпавших для 1000 кубиков.
