Как Осборн Рейнольдс пришёл к своему числу. Часть 1

Перевод классической научной работы, вышедшей в 1883 году.

Экспериментальное исследование прямого и волнистого режимов движения воды, а также закона сопротивления в параллельных каналах.

I Введение

1. Предмет и результаты исследования

Результаты исследования имеют практическое и философское значение.

Практическое значение относится к закону сопротивления движению воды в каналах. Получена новая форма этого закона, работающая для всех скоростей и диаметров, в виде уравнения из двух членов.

Философское значение связано с фундаментальными законами движения жидкости; основной результат исследования в том, что качественный характер (режим) течения жидкостей в контакте с твёрдой поверхностью определяется соотношением между определённой физической постоянной этой жидкости и скоростью, умноженной на линейный размер пространства, занятого жидкостью.

Основной результат лежит именно в философской плоскости.

Во введении не будем говорить о практическом аспекте; для наглядности кратко опишем цепочку рассуждений, которая определила ход исследования.

2. Основные свойства движения жидкостей

Во многих отношениях течение воды трудно постичь и ещё труднее описать, также как и силы, его сопровождающие. Но некоторые особенности бросаются в глаза, как будто напрашиваясь или бросая вызов теоретикам.

Например, связь между скоростью и сопротивлением твёрдого тела, полностью погружённого в жидкость, или воды, текущей в канале, можно выразить так: обычно сопротивление просто пропорционально квадрату скорости, а если это не так, то ещё проще – самой скорости.

Далее, внутреннее движение воды бывает двух видов – либо элементы жидкости следуют друг за другом по линиям движения, то есть наиболее прямым путям к месту назначения, либо завихряются по извилистым, максимально непрямым траекториям.

Большинство жидкостей либо прозрачны, либо однородно непрозрачны. В обоих случаях это не позволяет наблюдать их внутреннее движение. Разве что по поверхности воды можно понять, какой режим движения (прямой или волнистый) реализуется под ней, если только поверхность не подвержена другим возмущениям. Так, поверхность движущейся воды иногда выглядит как зеркало, когда предметы отражаются без искажений, а иногда как листовое стекло, когда отражения искажаются и гримасничают. Эти два вида поверхности соответствуют двум режимам движения. Можно показать это, добавив несколько полос сильно подкрашенной воды в чистую движущуюся воду. Даже если сначала они будут нерегулярными, в отсутствии вихрей они скоро вытянутся в ровные цветные полоски; а при наличии вихрей они наоборот будут завихряться и закручиваться, как дым.

3. Связь между основными свойствами движения жидкости

Эти свойства движения жидкости хорошо известны, и между ними прослеживается связь, однако на сегодняшний день не описана ни она, ни условия для их реализации. Эти условия связаны с некими закономерностями для сил. Для трубок размером более капилляра и для тел, движущихся в воде со сколько-нибудь заметными скоростями сопротивление меняется как квадрат скорости, тогда как в капиллярах и при маленьких скоростях реализуется линейный закон.

Уравнения гидродинамики описывают прямые, т.е. безвихревые движения. Согласно им, сопротивление от скорости зависит линейно. Но на сегодняшний день они не дают ответа, какие условия нужны для реализации прямого движения. Хотя в последние годы они используются для построения теории вихря, они не применялись для описания волнистого движения, т.е. когда вода представляет собой множество вихрей. На вопрос, почему сопротивление может меняться как квадрат скорости, они также не отвечают. Таким образом, с одной стороны теоретические результаты хорошо согласуются с экспериментами для волн и течения воды в капиллярных трубках. С другой, гидродинамическая теория пока, во-первых, не может объяснить, почему она описывает эти явления и во-вторых никак не объясняет закон сопротивления для больших тел, двигающихся с разумными скоростями в воде, или для воды в каналах разумного размера.

То, что теория по случайности способна объяснить одни явления и совершенна неспособна описывать другие, позволяет предположить, что существуют фундаментальные законы движения жидкости, которые она не учитывает. И несколько лет назад мне представилось, что тщательное исследование связи между вышеупомянутыми четырьмя основными свойствами и условий, при которых они реализуются, должно стать ключом к этим неизвестным законам.

4. Пространство и скорость

Тот факт, что для достаточно больших трубок или скоростей сопротивление меняется как квадрат скорости, а для капилляров и маленьких скоростей – как скорость, свидетельствует о фундаментальном и важном влиянии неких свойств жидкостей, не учтённых в теории гидродинамики.

Поскольку в механической философии нет абсолютного пространства или времени, то гипотеза о том, что характер течения жидкостей как-то зависит от абсолютного размера или абсолютной скорости, лежит вне рамок законов движения. Если жидкости всё же подчиняются этим законам, тогда то, что кажется зависимостью режима движения жидкости от абсолютного размера трубки или абсолютной скорости погружённого тела – это в реальности зависимость от размера трубки по сравнению с размером какого-то другого объекта и скорости тела по сравнению с какой-то другой скоростью. Что это за эталонные объект и скорость – не очевидно. Однако ответы на эти вопросы были найдены, когда были открыты условия, при которых реализуется волнистый режим движения.

5. Влияние вязкости на режим движения жидкости

В чистой воде наблюдать вихри очень трудно; до определённого момента определение вязкости жидкости также представляло проблему. Благодаря этим обстоятельствам, лишь недавно был  установлен очень важный факт: более вязкая жидкость менее подвержена завихрениям и волнистому движению. Выразим это более точно. Если – вязкость и – плотность жидкости, то для воды быстро убывает с ростом температуры: При 5°C вдвое больше, чем при 45°C. И по моим наблюдениям стремление воды к завихрениям с температурой быстро увеличивается.

Таким образом, это обстоятельство связывает изменение закона сопротивления с рождением и развитием вихрей, а тогда стандартное расстояние и стандартная скорость должны определяться физическими свойствами жидкости. Для продолжения исследования нужно обратиться к молекулярной теории жидкостей, но это пока не входит в мои цели. Здесь достаточно отметить, что размерность или – это произведение расстояния и скорости.

Всегда трудно отследить влияние одной идеи на другую. Но можно отметить, что идея о размерных параметрах, как в случае зависимости режима движения от размера трубки и скорости жидкости пришла ко мне после исследования  транспирации газов, когда была установлена зависимость закона транспирации от соотношения между размером канала и средним пробегом молекул газа.

6. Размерные параметры в уравнениях движения

Уравнения движения тщательно изучены, в частности, профессором Стоксом, поэтому найти в них что-то новое или ошибки было маловероятно. Но мне показалось, что в них можно найти что-то, указывающее на зависимость режима движения от соотношения размерных параметров и внешних условий течения. Была обнаружена явная связь, причём без интегрирования.

Предположим, режим движения зависит от одного скоростного параметра , пусть это будет средняя скорость в канале, и от одного параметра длины , пусть это будет радиус трубы; если теперь, как это обычно делается, убрать из уравнений давление, ускорения выражаются через члены двух типов. Один имеет множитель , а другой . Относительные значения этих членов изменяются соответственно как и .

Как раз подобную связь я и искал. Конечно, без интегрирования уравнения давали только соотношение, ничего не говоря о том, каким образом от него зависит режим течения.

Вероятно, если вихри вызваны только одной причиной, интегрирование покажет, что их рождение обусловлено неким определённым значением .

7. Что вызывает вихри?

Есть две возможные причины перехода от прямого движения к волнистому. Лучше всего описать их на языке гидродинамики. Отличие между ними весьма тонкое, но фундаментальное, что приводит к существенно разным результатам.

Как указал профессор Стокс в 1843 году, общий механизм перехода от стационарного движения к вихревому заключается в том, что при некоторых условиях стационарное движение становится нестационарным, и тогда бесконечно малые возмущения могут возбудить волнистое движение. Обе вышеупомянутые причины относятся к этому виду, но отличаются ролью, которую играет в неустойчивости вязкость.

Представим невязкую жидкость, свободно скользящую по твёрдым телам, и сравним её с вязкой:

1. Допустим, невязкая жидкость неустойчива, а вязкая – устойчива. В этом случае причина вихрей – неустойчивость идеальной жидкости, а вязкость работает в сторону устойчивости.

2. Допустим, невязкая жидкость устойчива, а вязкая – неустойчива. В этом случае причина неустойчивости – вязкость.

Для меня было очевидно, что выводы, которые я сделал из уравнений движения, прямо относятся к случаю 1, и я не мог понять, как вязкость может вызывать неустойчивость. В то же время не было уверенности в том, что случай 1 – наиболее общий. Эта неуверенность происходила из различных соображений, а особенно из моих наблюдений того, как при строго фиксированных условиях движения вихри появляются очень разными способами. Проиллюстрируем это.

Когда вся вода в канале движется в одном направлении, скорость максимальна посредине и уменьшается до нуля на стенках, как показано на рисунке 1. При этом вихри появляются неохотно и беспорядочно. Тогда как если вода на одной стороне канала движется в противоположную сторону, чем на другой, как показано на рисунке 2, то вихри в середине появляются регулярно и легко.

Рисунок 1.

Рисунок 2.

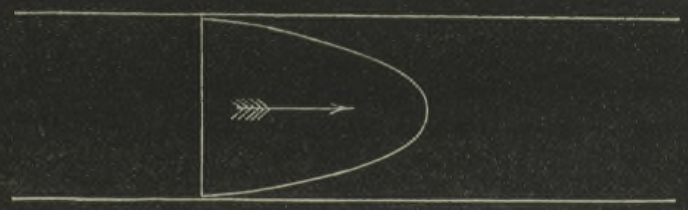
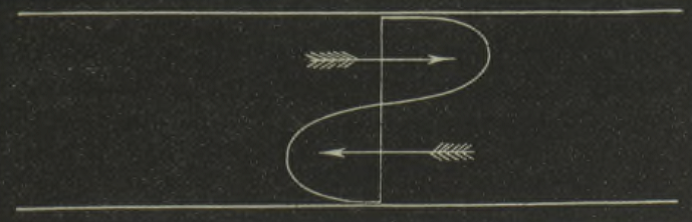
8. Методы исследования

Далее можно было пойти по теоретическому либо практическому пути. Теоретический метод подразумевал интегрирование уравнений нестационарного движения, что было мало перспективно, учитывая их неподатливость.

Практический метод подразумевал проверку связи между и . Так как вид закона был очень прост, это было как минимум более перспективное поле для исследований.

Закон для течения в прямой гладкой трубе представлялся одновременно наиболее простым случаем и наиболее критическим тестом.

Все имевшиеся на тот момент обширные экспериментальные данные по сопротивлению воды в трубах были в одном отношении неполны: в одних сопротивление менялось как квадрат скорости, в других – как сама скорость. Данных о том, при каких условиях реализуется тот или иной режим, не было.

Далее, хотя как было показано, вихри должны были объяснить изменение сопротивления как квадрата скорости, чётких экспериментальных наблюдений вихрей в каналах не нашлось. Также не было данных о том, происходит ли их появление одновременно с изменением закона сопротивления.

Предполагалось, что на все следующие вопросы, будет получен положительный ответ:

1. Какому соотношению между диаметром канала и скоростью воды соответствует изменение закона сопротивления? Происходит ли это при определённом значении ?

2. Зависит ли это изменение от температуры, т.е. вязкости воды? Происходит ли это при определённом значении ?

3. Бывают ли вихри в параллельных каналах?

4. Стационарное движение существует до некоторого критического значения, а потом появляются вихри?

5. Вихри появляются при определённом значении ?

6. Вихри сначала рождаются маленькими, и потом растут, или появляются внезапно?

Значение последнего вопроса не так очевидно; но, как мы увидим, отрицательный ответ на него (несмотря на положительные ответы на остальные вопросы) для определённого класса движений заставил меня пересмотреть гипотезу о причине неустойчивости.

Поставленные вопросы предполагали два метода экспериментов:

1. Измерение сопротивлений и скоростей при разных диаметрах и температурах воды.

2. Визуальное наблюдение появления вихрей в трубах или открытых каналах.

Оба метода были применены, но так как вопрос о вихрях был менее изучен, то первым был применён второй метод.

9. Визуальные наблюдения

Наиболее важные эксперименты этого типа относятся к течению воды в стеклянных трубках в одном направлении. Помимо них в той же трубке исследовалось течение в противоположных направлениях, а также течение в плоском канале бесконечной ширины. Последние были проведены из-за одного случайного наблюдения, сделанного в 1876 году в ходе экспериментов по подавлению ветровых волн с помощью масла. Это наблюдение значительно повлияло на ход данного исследования, поэтому стоит сначала рассказать о нём.

10. Вихри, вызванные ветром, под поверхностью воды, смоченной маслом

Если разлить несколько капель масла на наветренной стороне пруда при сильном ветре, они растекаются по всему пруду и полностью гасят волны. Лист масла, если его можно так назвать, растекается быстрее ветра, и на достаточно большом участке около наветренного берега поверхность воды выглядит как зеркальное стекло. На большем удалении от берега наблюдаются нерегулярные волны, которые можно сравнить с листовым стеклом. Тогда это было интерпретировано как вихри под поверхностью воды.

Этот предварительный вывод подтверждается следующим наблюдением. При наличии масляной плёнки на достаточном расстоянии от наветренного берега под поверхностью всегда наблюдались вихри, даже если ветер был слабым. Однако это расстояние быстро увеличивалось при ослаблении ветра, так что уже при 30–60-ти метрах вихри появлялись и следовали за ветром.

Я не придумал, как можно идентифицировать вихри без использования масла. Сначала я считал, что волны могут присутствовать, даже если их не видно, но после тщательных исследований оказалось, что их не было. Не будем сейчас подробно обсуждать эти результаты, но как будет видно, они имеют большое значение касательно причины неустойчивости.

11. Эксперименты с цветными полосами в стеклянных трубах

Эти эксперименты были проведены в начале 1880-го года. Чистовые данные получены в трубках № 1, 2 и 3 диаметром около 25, 12 и 6  мм и длиной около 1370 мм. Чтобы вода втекала в них без возмущений, на входе трубки устанавливалась воронка. Трубки были погружены в большой стеклянный бак, из которого вода в них и втекала. Было сделано так, чтобы вместе с чистой водой в трубки втекала также полоса или полосы сильно подкрашенной воды. Были получены следующие результаты:

1. При низких скоростях полоска в трубке развивается в красивую прямую линию.

   

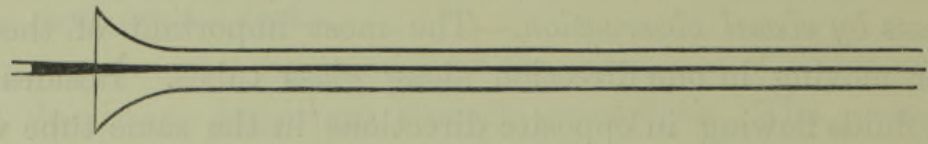
   Рисунок 3.

2. Если не дать воде в баке изначально устаканиться, при низких скоростях полоска двигается относительно трубки, но волнистости не наблюдается.

3. При постепенном увеличении скорости, в некоторой точке трубки (которая всегда находилась на значительном расстоянии от входа), полоска вдруг смешивается с окружающей водой, и вся трубка заполняется подкрашенной водой.

   

   Рисунок 4.

   Увеличение скорости приближает точку распада к входу в трубку, хотя в исследованном диапазоне скоростей она до него не доходила.

   В свете электрической вспышки в окрашенной воде видны завитки, вызванные вихрями.

   

   Рисунок 5.

   Таким образом, эти данные положительно отвечают на вопросы 3 и 4, то есть подтверждают существование вихрей в каналах и критической скорости.

   На вопрос 6 они отвечают отрицательно, то есть при достижении критической скорости вихри появляются не постепенно.

   Чтобы ответить на вопрос 5, то есть о законе для критической скорости, были тщательно измерены диаметры трубок, температура и расход воды.

4. При постоянной температуре воды и если дать ей изначально максимально устаканиться, то скорость, при которой появляются вихри, почти в точности обратно пропорциональна диаметру трубки.

5. Во всех трубках критическая скорость уменьшается с ростом температуры в диапазоне от 5 до 22 °C; закон этого уменьшения, насколько можно судить, согласуется с экспериментами Пуазейля. Есливыражена в градусах Цельсия, то по Пуазейлю . Если D – диаметр трубки, то в метрических единицах критическая скорость , где,. Это полностью отвечает на вопрос 5.

В ходе экспериментов было замечено много вещей, которые не могут быть упомянуты здесь, но нужно отметить два обстоятельства, которые свидетельствуют в пользу отрицательного ответа на вопрос 6. Во-первых, величина критической скорости оказалась гораздо больше, чем ожидалось для каналов этих размеров. Также, сопротивление менялось как квадрат скорости при гораздо меньших скоростях, чем когда появлялись вихри, при этом вода в баке была спокойна. Во-вторых, критическая скорость оказалась очень чувствительна к возмущениям в воде на входе в трубку. Чтобы получить непротиворечивые результаты, пришлось приложить огромные усилия для установления равномерной температуры в баке и неподвижности воды. Это указывает на то, что при больших возмущениях стационарное движение было неустойчивым задолго до достижения критической скорости. Это подтверждает то, что вихри рождаются сразу большими.

Часть 2.