Elliptic curves are very simple. The Elliptic Curves Digital Signature Algorithm (ECDSA), which works on top of their properties, is used in most blockchains like Bitcoin, Ethereum, etc., and is even simpler. But it’s challenging to find a good explanation on the internet and build all the pieces together. But here it is! In this article, we will.
We will go through all the concepts needed to understand and implement this algorithm — one by one. By the end of this article, we will have a fully functioning demo from scratch, which can extract the public key from the private key, sign a message, and verify that the signature is correct. This implementation will only use the concepts described in this article. Moreover, it will take less than 100 lines of code.
This article is targeted mainly at developers like myself, who want to finally understand ECDSA, but it will also be very useful for everyone else. It requires knowing no more than middle school math.
I highly recommend following it step by step. If you want, you can grab a piece of paper and a pen and repeat all the steps in this article. It would be even better! If you’re not a programmer, you can ignore some pieces of code. If you are, I recommend re-writing the code on your own and practicing!
The article consists of 6 parts; each part uses the concepts of the previous parts (except part 2):
I: The essentials of elliptic curves
II: The essentials of finite fields
III: Elliptic curves over finite fields
IV: Practical use of it: ECDSA
V: The implementation
VI: Live Demo
Let’s start here!
PART I: The Essentials of Elliptic Curves
We’re all probably familiar with all those graphs on coordinate grids where the y variable somehow depends on x. For example, y = x, y = x², and so on. Most probably, we all have some experience with it. Let’s look at them:
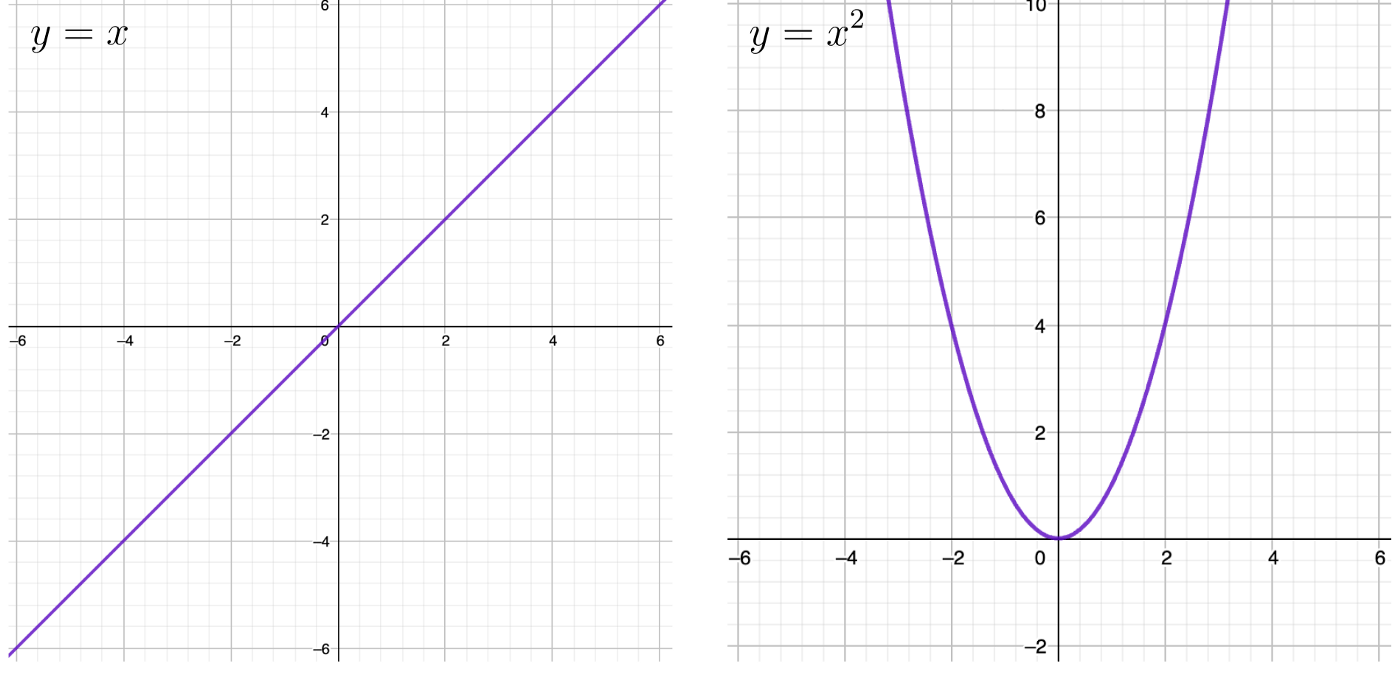
The equation for an elliptic curve is not much different! It has the form of y² = x³ + ax + b. What are a and b? Just some arbitrary constants. Let’s see how it looks with a = 0, b = 7, just like in the Bitcoin curve:
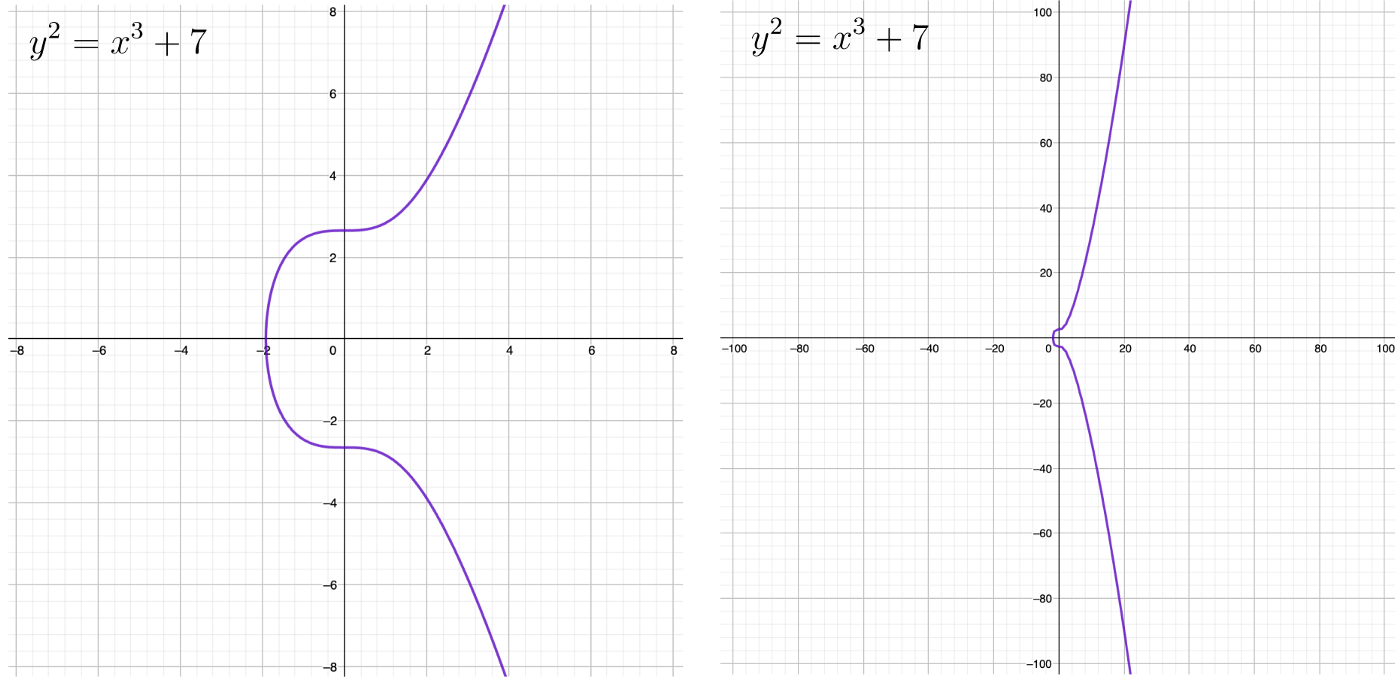
It has the following three super important properties upon which everything works:
This is where it may get hard to follow and understand why. You may even think this is something incoherent and irrelevant. But please trust me. These properties will lead us to a very amazing result! But now let’s pretend that we’re just having fun without a purpose.
The elliptic curve is symmetric along the x-axis. It means that for any point on the curve A, we can get its mirror point, called -A, by simply mirroring its y coordinate:
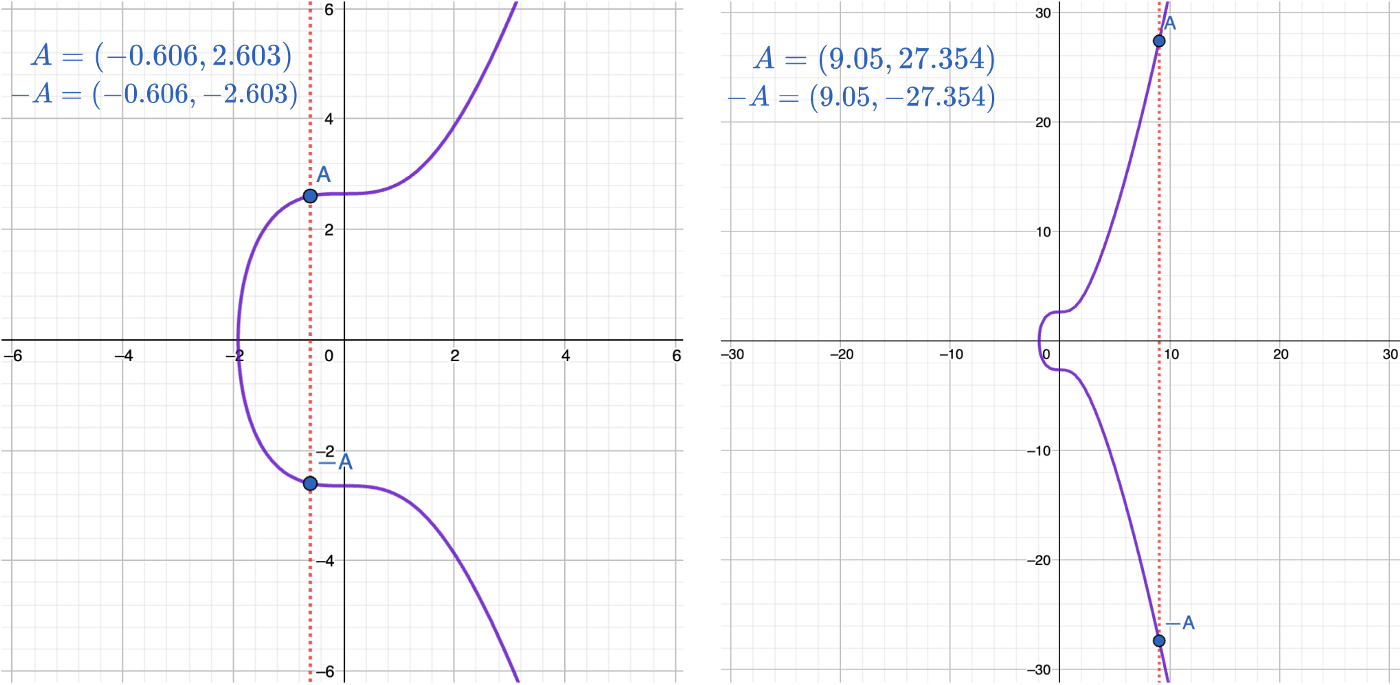
If we draw a line through any of two points not lying on a vertical line, it will intersect the curve at exactly one more point! Let’s draw a line through the A and B points and call the third point — C. Then, let’s reflect it to get the point C:
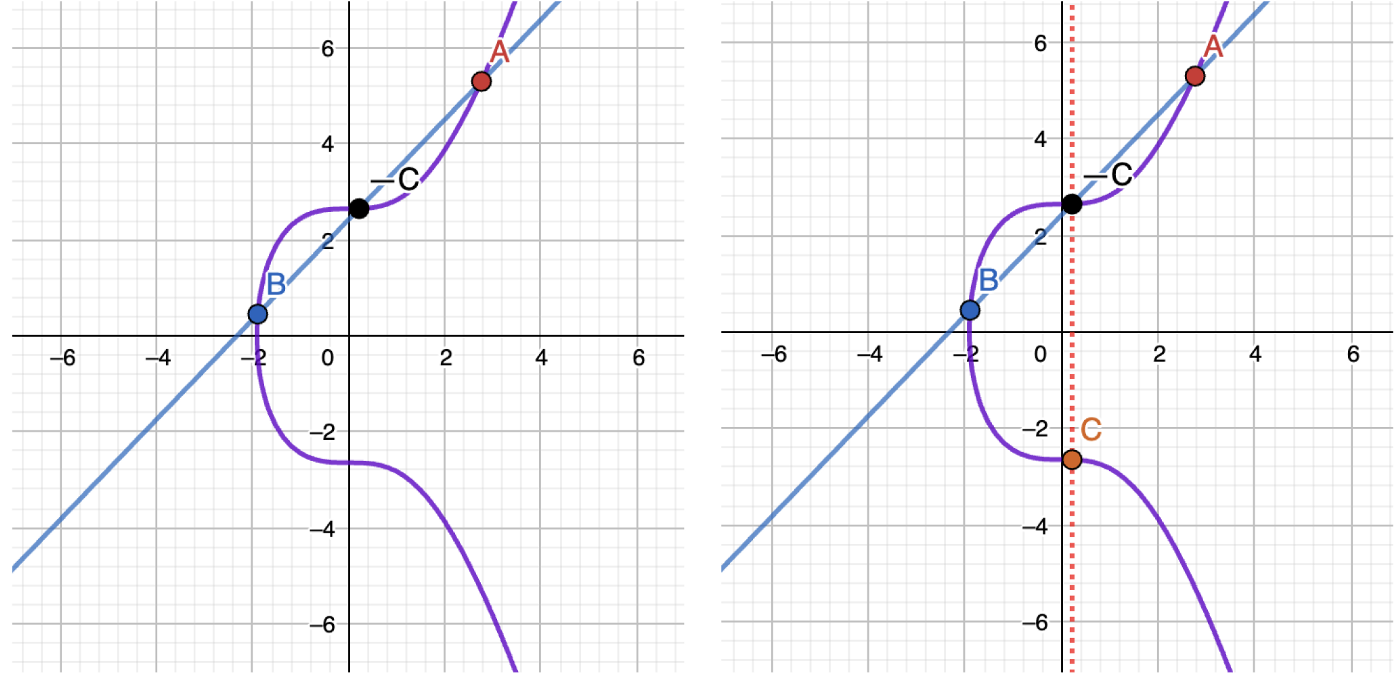
Another example:
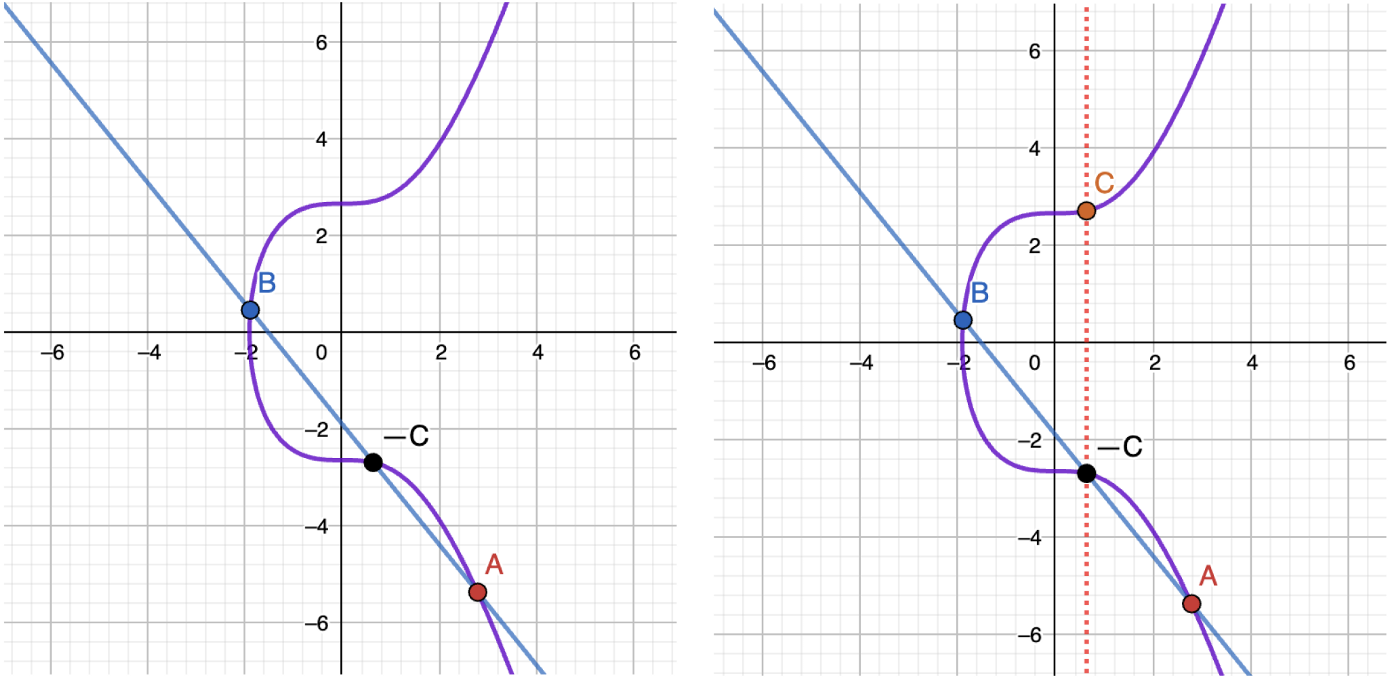
This C point is called the sum of A and B. So A + B = C.
If we draw a tangent line through any point A lying on a curve, it will intersect the curve at exactly one point. We will call this point -2A. We already know how to get 2A:
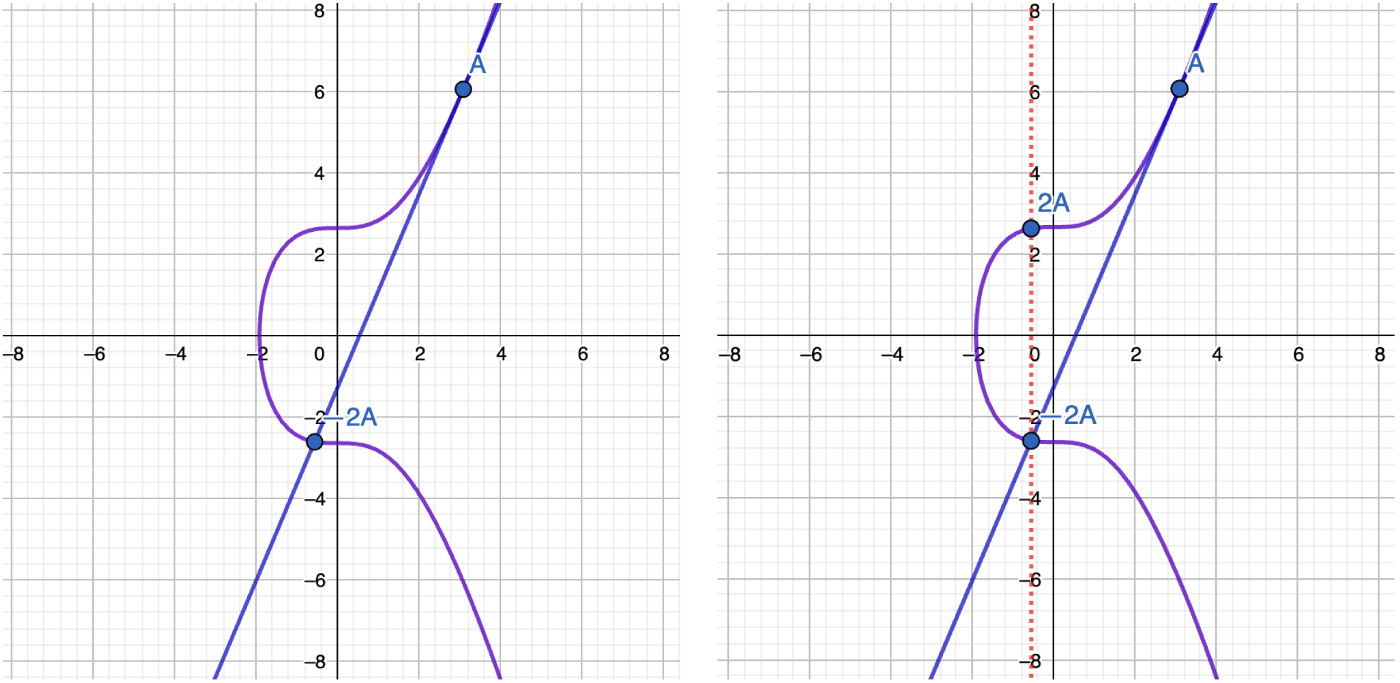
The easiest way to think about a tangent line is to imagine it intersecting A point twice. As if it intersects the curve not at two points but three: A, A, -2A.
That’s it! We defined three mathematical operations on the elliptic curve: multiplying a point by -1, adding two points together, and doubling a point.
And here is where the algebra of elliptic curves starts working.
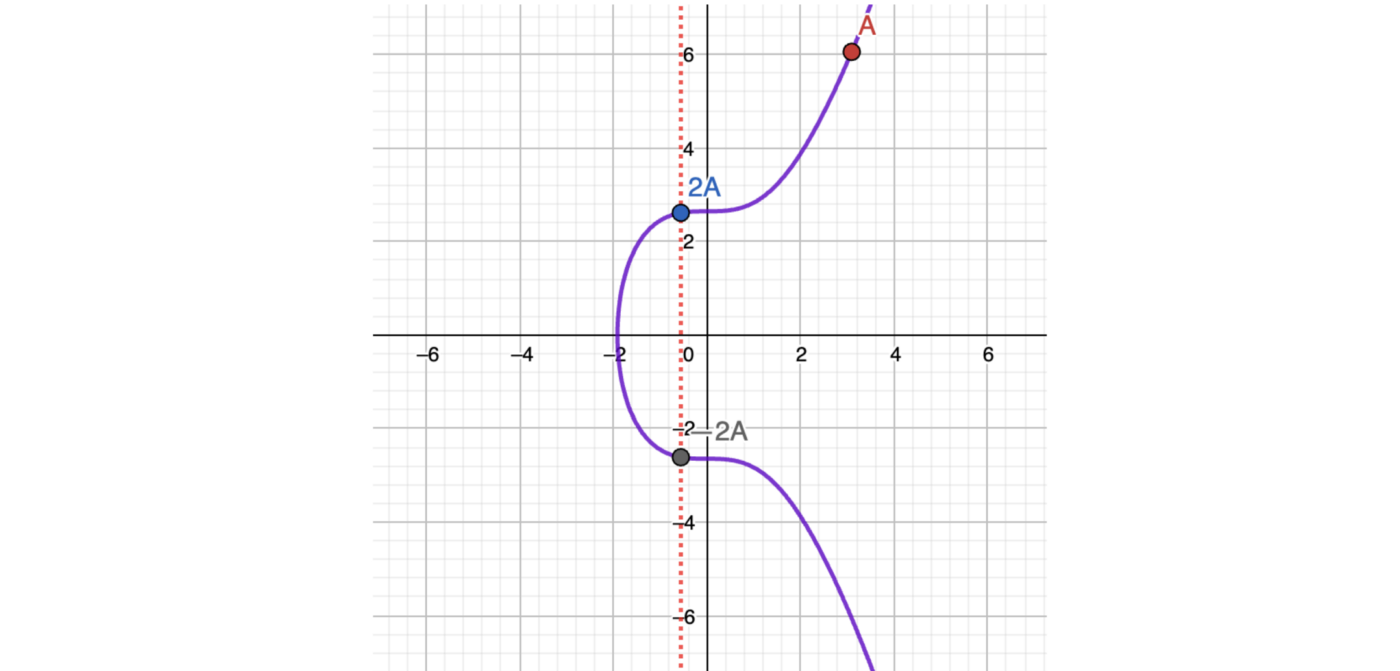
Now we have the following picture with points A, 2A, and -2A:
Let’s draw a line through A and 2A. The third point that we’ll get is -3A. Then just reflect it to get 3A:
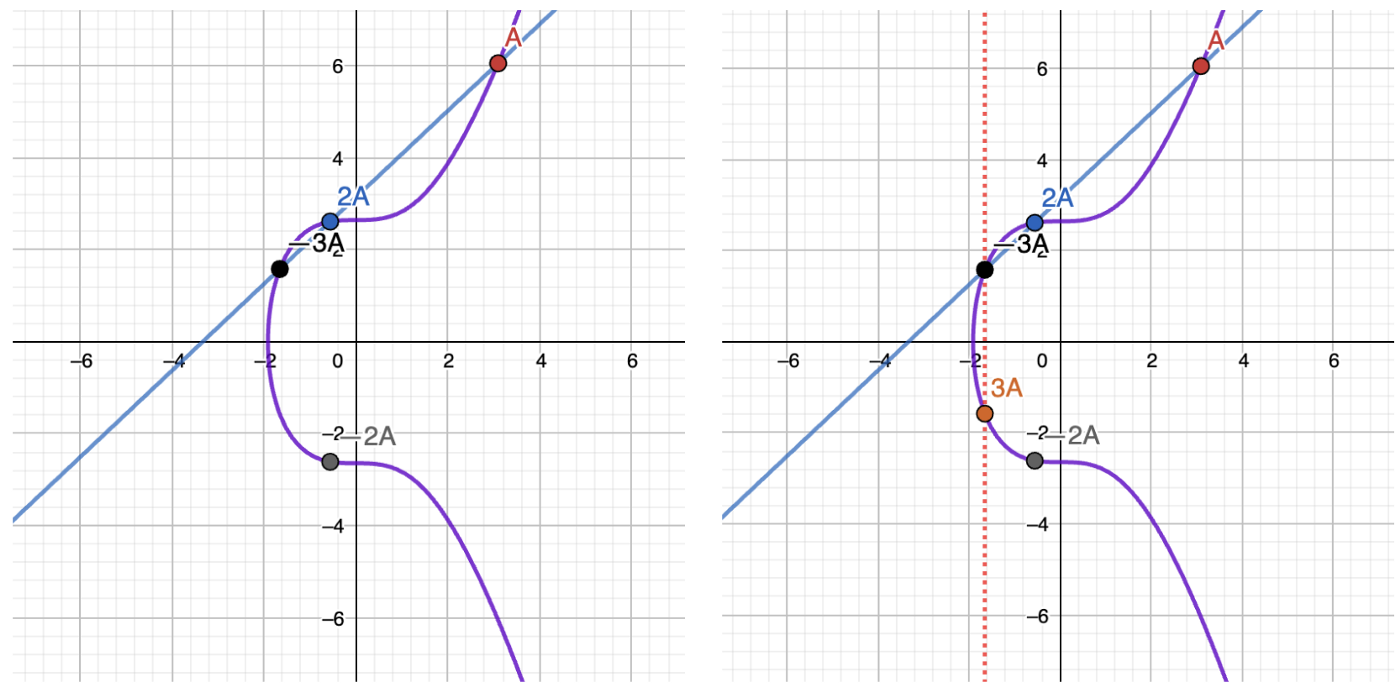
You probably don’t yet understand why we’re doing all of it. Just look at one more step. What if we try drawing a line between 3A and -2A?
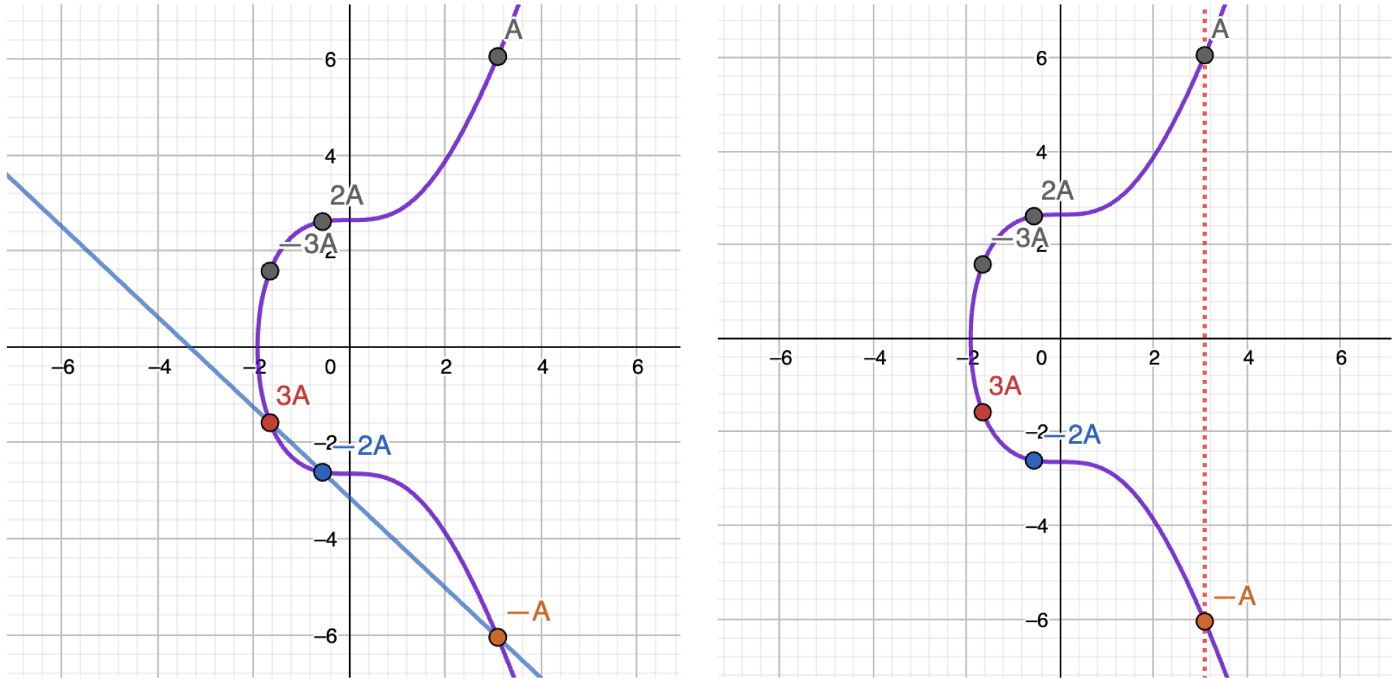
Do you see the magic? By drawing a line between 3A and -2A we’re getting the -A point, which is the reflection of our original A point along the x-axis!
What we just defined in the three clauses above, is the algebra of elliptic curves.
Just try to understand the power of those three operations: essentially now we can perform operations on the points lying on a curve as if they’re not points, but just numbers!
What we can do with points on a curve:
Addition of two points (A + B)
Subtraction of two points A — B = (A + (-B))
Doubling of a point (multiplication by two) 2A
Multiplying by any integer (by combining the previous operations together, we can get any integer * Point)
What we can’t do:
Multiplication of two points
Division of a point over another point
Division of a point over a scalar value
For example, to get 10A:
2A = A + A
4A = 2A + 2A
8A = 4A + 4A
10A = 8A + 2A
It’s also good to notice that the calculation may be performed in a logarithmic amount of operations. So the approximate amount of operations needed for calculating n * Point is O(log2(n))!
Eventually, we can multiply a point by any integer, but there is no way to get the integer back! This is the gist of it! And this is what makes the elliptic curves very good for cryptography. And it works for infinitely large numbers.
The only drawback, for now, is the need to draw it. But of course, there are mathematical formulas for reflecting a point, for addition, and for doubling a point:
Multiplying the point by -1. If we have a point A(x, y), we can easily get -A by multiplying its y coordinate by -1. -A(x, -y). Example:
-1 * A(2, 2) → -A(2, -2)
-1 * A(1, -1) → -A(1, 1)
-1 * A(5, 8) → -A(5, -8)
-1 * A(5, -8) → -A(5, 8)Adding two points together. We can add two points together, but with one condition: they should not lie on a vertical line (their x coordinates should not be equal). This is the formula for adding A and B (A + B = C):
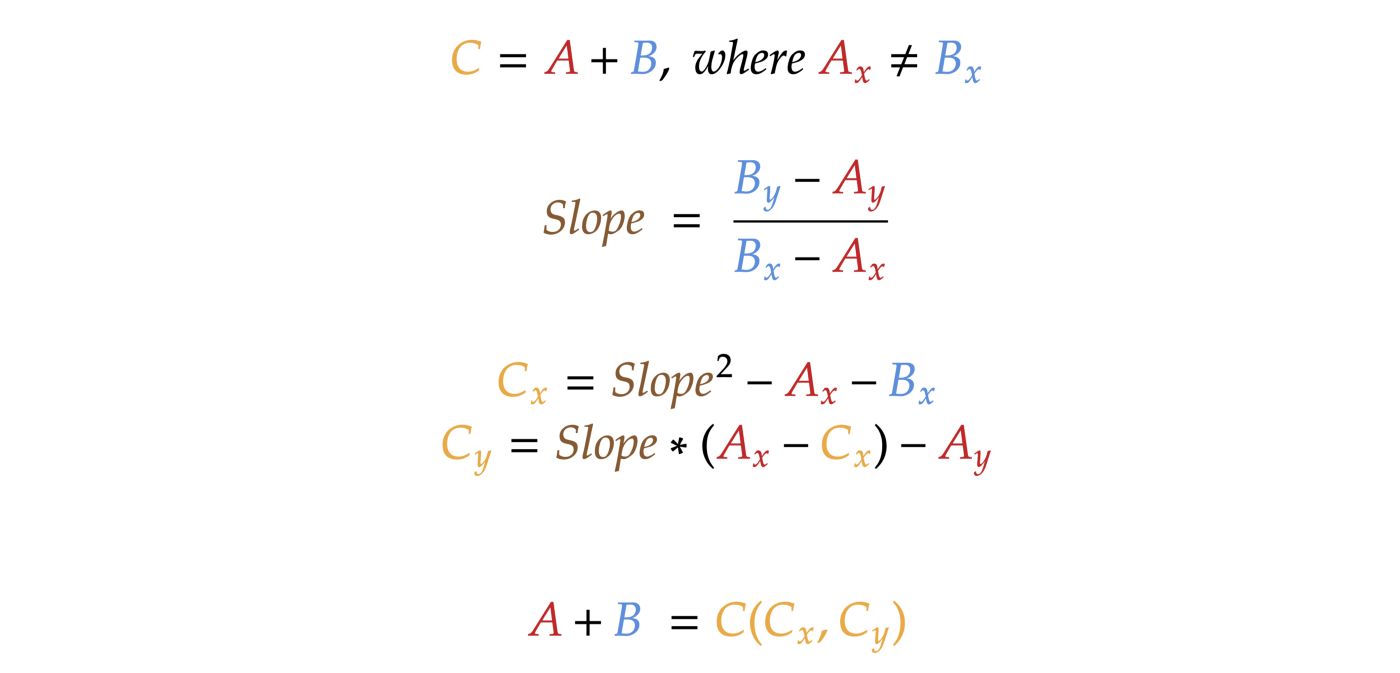
Adding a point to itself (multiplying a point by 2). This is a very similar operation to the addition of two points but slightly different:
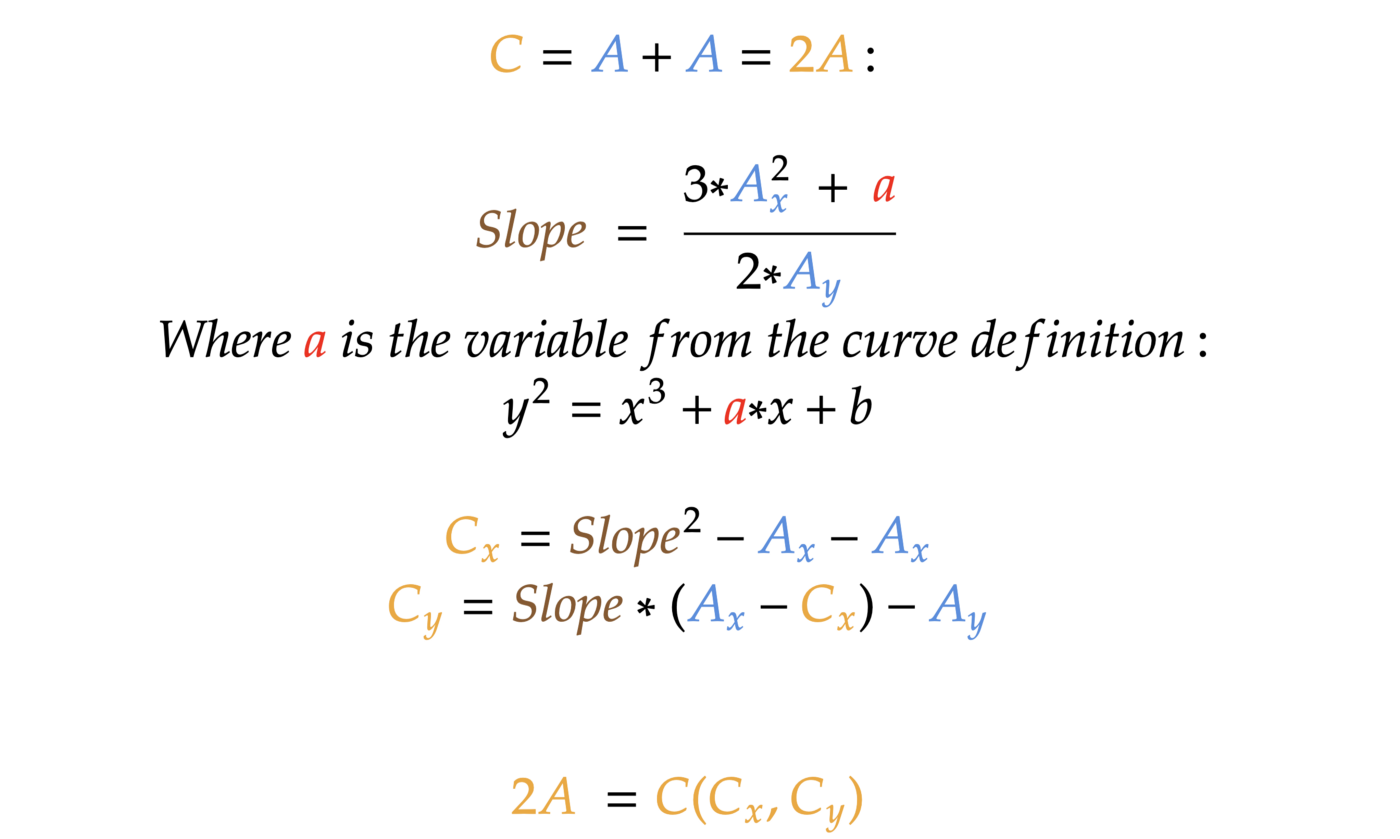
That’s it! Time to practice!
Let’s try adding A and B here (let’s use approximation to 3 points after a comma):
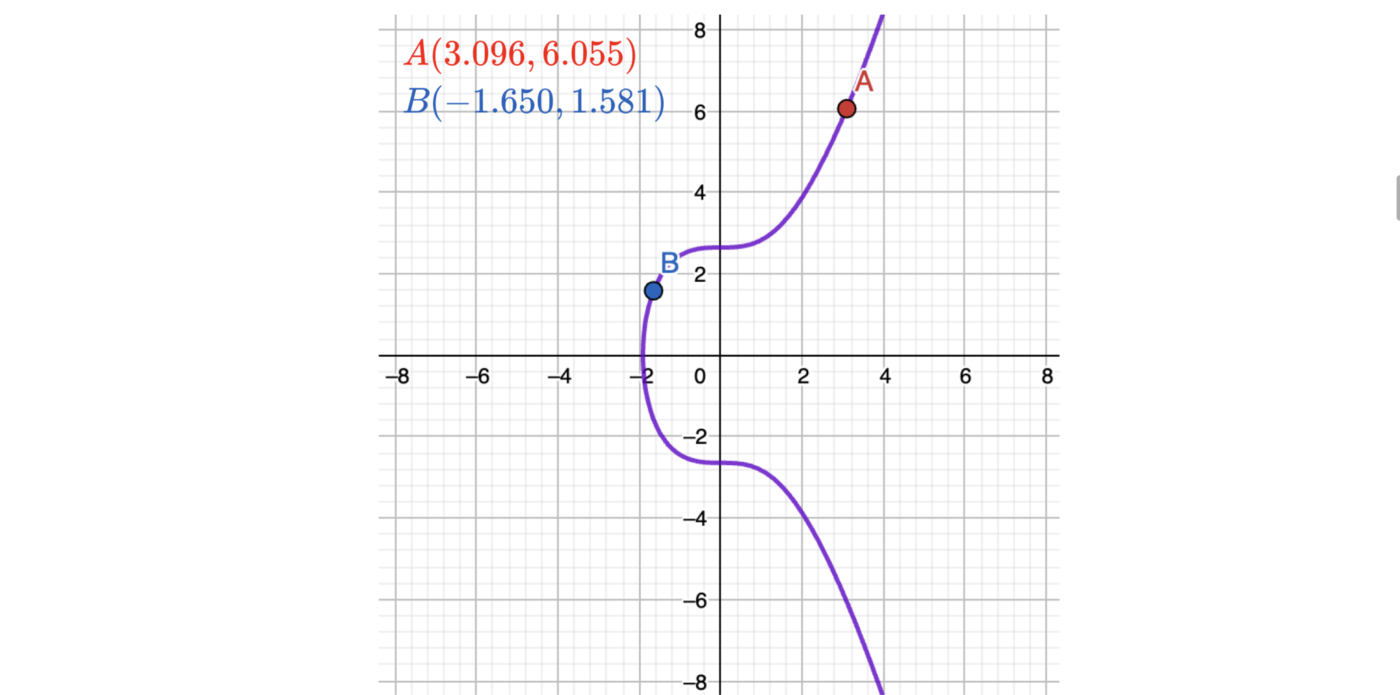
According to the formula defined above for adding two points,

Now let’s find our point C graphically:
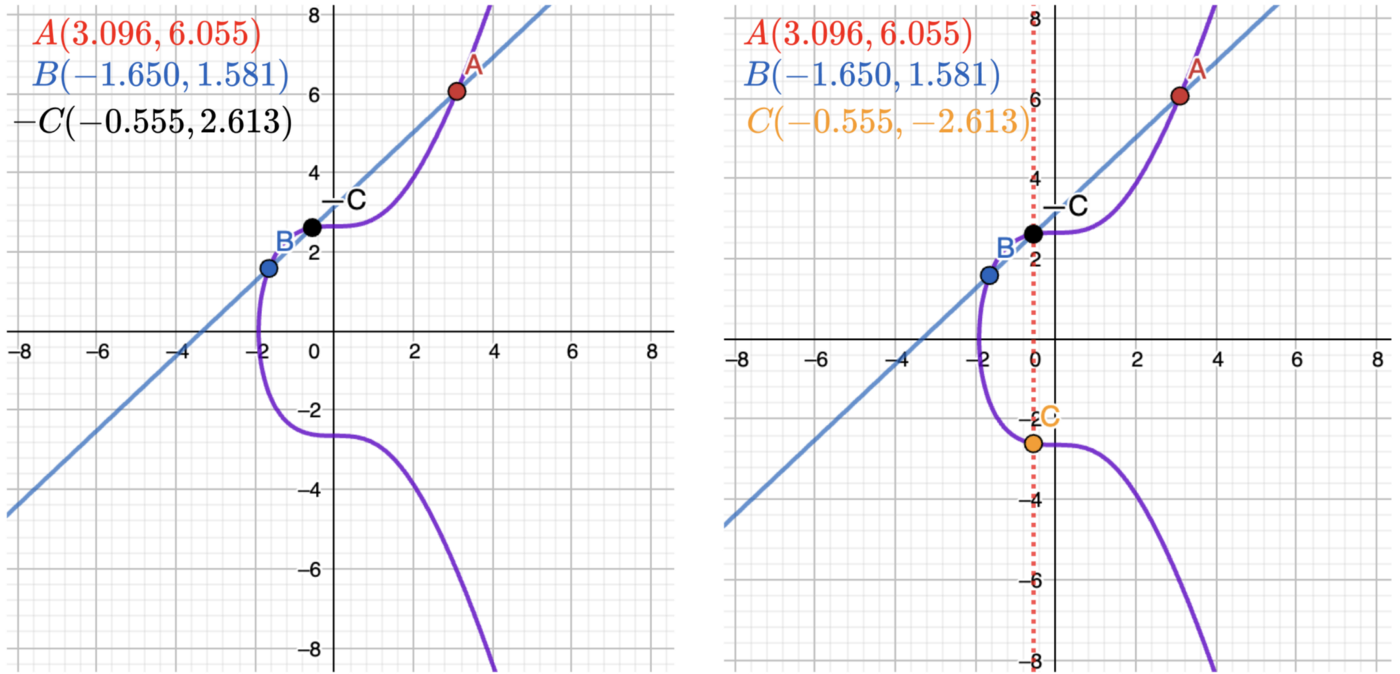
It works! Yes, with a minor proximity issue, because of rounding. But it works! For better understanding, I recommend you try to perform all those operations on your own.
This was all we needed to know about elliptic curves and the operations on them that we need to be able to perform!
Everything is fine, but we need a couple more properties for building a cryptography system.
Part II: Finite fields
We don’t need to study everything about finite fields. All we need here is to understand a couple of essential properties to move on and be able to operate on a certain “algebra” of finite fields.
Have you heard of the modulus operation? If you’re a programmer, you probably did. This is just a reminder of division, and in programming languages, it’s usually expressed as a % (or mod) operator. For example:
2 mod 11 = 2
10 mod 11 = 10
11 mod 11 = 0
13 mod 11 = 2
14 mod 11 = 3
If we try numbers from 0 to 33 mod 11, we will get these numbers:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0
It works like a clock. We can call it a finite field of order 11.
We need to know just four properties:
The order of multiplication doesn’t matter.
a * b * c mod n is the same as (a mod n) * (b mod n) * (c mod n) mod n, which is the same as (a * b mod n) * c mod n.
Example:
6 * 7 * 8 mod 11 = 336 mod 11 = 6, same as:
(6 * 7 mod 11) 8 mod 11 = (42 mod 11) 9 mod 11 = 9 * 8 mod 11 = 72 mod 11 = 6Negative number mod n is the same as n-(|negative number| mod n).
Examples:
1) -4 mod 11 = 11-(4 mod 11) = 11–4 = 7
2) -7 mod 11 = 11 — (7 mod 11) = 11–7 = 4
3) -9 mod 11 = 11 — (9 mod 11) = 11–9 = 2
4) -2 mod 11 = 11 — (2 mod 11) = 11–2 = 9
5) -13 mod 11 = 11 — (13 mod 11) = 11–2 = 9“Multiplicative inverse”: for any a, there is a number b, such as ab mod n = 1.
If a * b mod 11 = 1, a is called the multiplicative inverse of b modulo n, and vice versa: b is called the multiplicative inverse of a modulo n.
Examples:
1) 5 * x mod 11 = 1. Let’s try values for x one by one, and we will find out x = 9, because 5 * 9 = 45, 45 mod 11 = 1. So 9 is the multiplicative inverse of 5 modulo 11.
2) 7 * x mod 11 = 1. Let’s try our brute force again, and we will find out x = 8. 8 is the multiplicative inverse of 7 modulo 11.
3) 10 * x mod 11 = 1. x = 10. So 10 is the multiplicative inverse of 10 modulo 11.
Usually, the multiplicative inverse is found by the extended Euclidean algorithm, but it’s a matter of a separate article. So, for now, let’s just use brute force. Also, n must be a prime number!The division is the same operation as multiplication by the multiplicative inverse! The last and most important property:
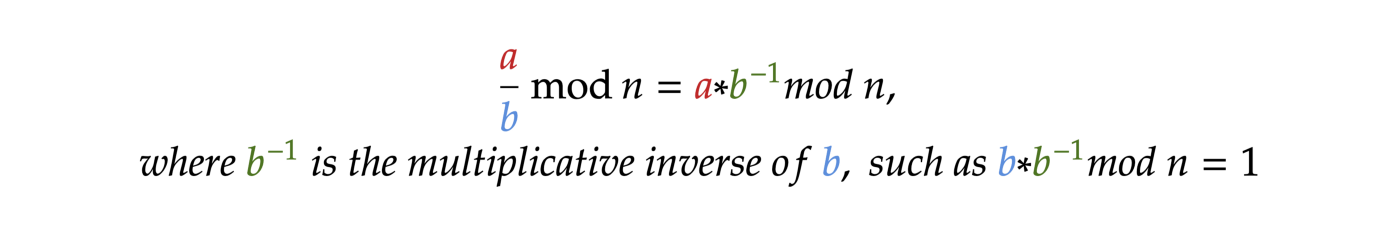
So, when we need to deal with division mod n, we can easily calculate it. Let’s see an example:
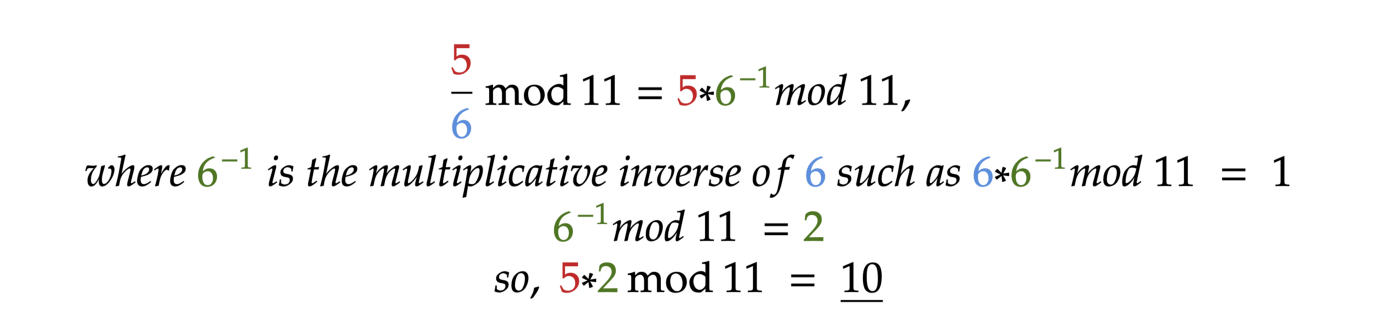
That’s it! Now we know how to operate on finite fields “algebra”.
Part III: Elliptic curves over finite fields
Here’s where it becomes less obvious and a little harder to understand. But this is exactly how elliptic curves are used in cryptography. What we need to do is exactly what is said in the title: put our elliptic curve over a finite field.
So, here is how our formula changes:
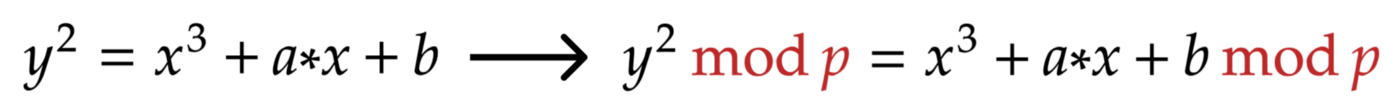
Everything is the same as in the original formula but now both parts of the equation are now under the modulo p.
Let’s use the elliptic curve with the following configuration for our examples:
a = 0
b = 7
p = 11
Let’s find all the points on this curve running this code:
const a = 0;
const b = 7;
const p = 11;
for (let x = 0; x <= p; x ++) {
for (let y = 0; y <= p; y ++) {
if (y**2 % p === (x**3 + a * x + b) % p) {
console.log(`(${x}, ${y})`);
}
}
}It’s javascript, so you can run it even in the browser.
Here is the result: (2, 2), (2, 9), (3, 1), (3, 10), (4, 4), (4, 7), (5, 0), (5,11), (6, 5), (6, 6), (7, 3), (7, 8)
Let’s see what it looks like on a coordinate grid:
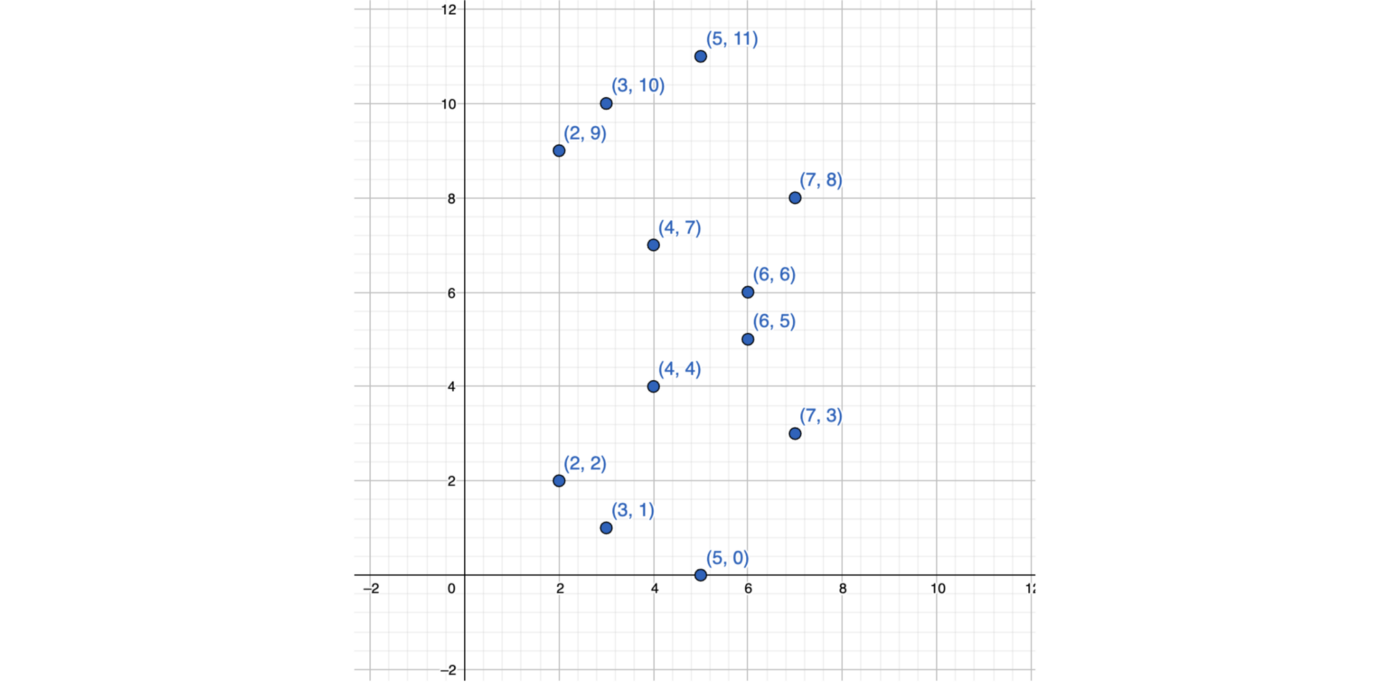
Let’s try a=0, b=7, p=23:
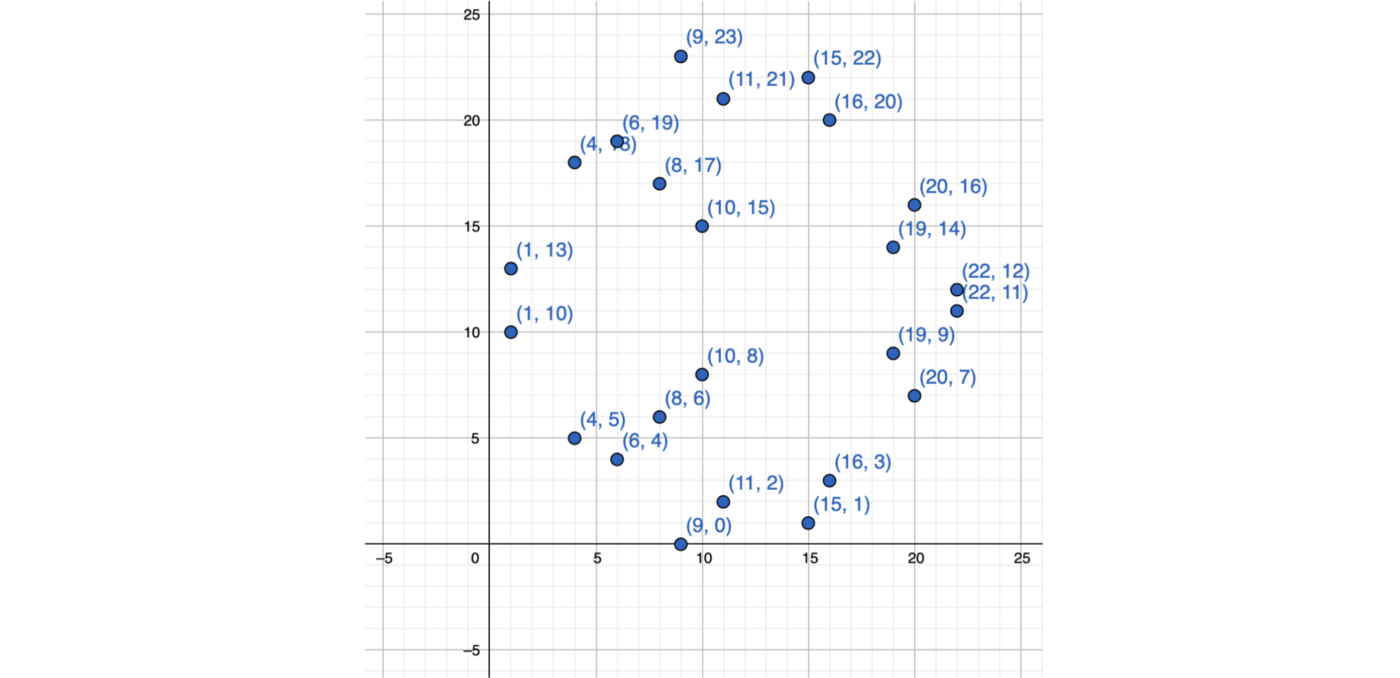
Doesn’t look like anything, right? No distinguishable shape.
But! What turns out is that it preserves all the properties and formulas of the “original” elliptic curve!
So now we’ve got an elliptic curve that doesn’t look like an elliptic curve. But! It has a finite set of points and most importantly, works like an elliptic curve.
We need to slightly modify our formulas from PART I with respect to mod p:
Multiplying a point by -1:
If we have a point A(x, y), we can easily get -A by multiplying its y coordinate by -1 modulo p.
Example:
1) -1 * A(2, 2) → -A(2, -2 mod 11) = -A(2, 9)
2) -1 * A(2, 9) → -A(2, -9 mod 11) = -A(2, 2)
3) -1 * A(6, 5) → -A(6, -5 mod 11) = -A(6, 6)
4) -1 * A(6, 6) → -A(6, -6 mod 11) = -A(6, 5)Adding two points together:

Adding a point to itself:
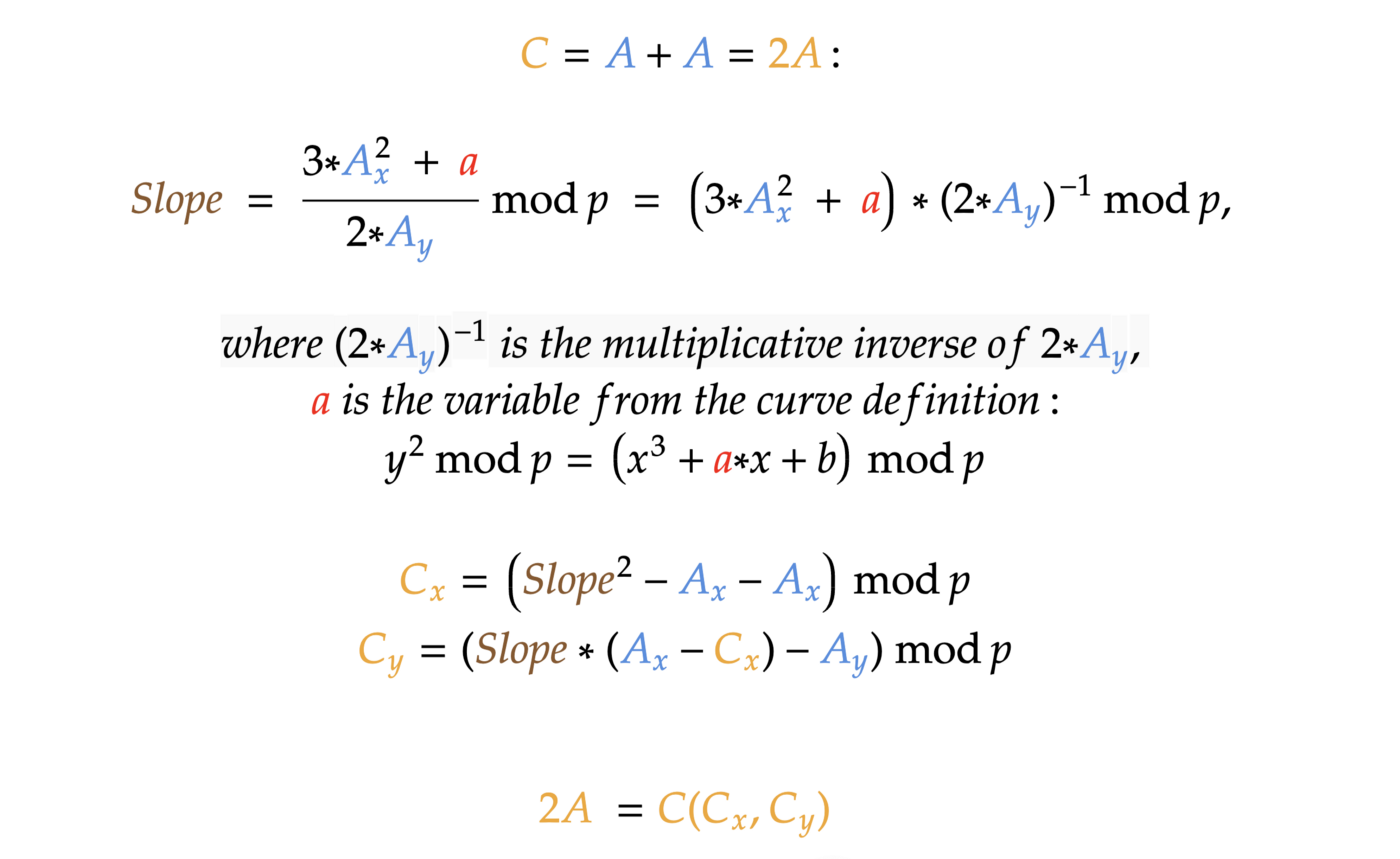
If you don’t yet understand the concept of multiplicative inverse, please, go back to PART II and check it once more.
That’s it! Time to practice!
For our examples, we will use the elliptic curve with a=0, b=7, and order p=11. Let’s pick a point C(7, 8) and calculate 2C:
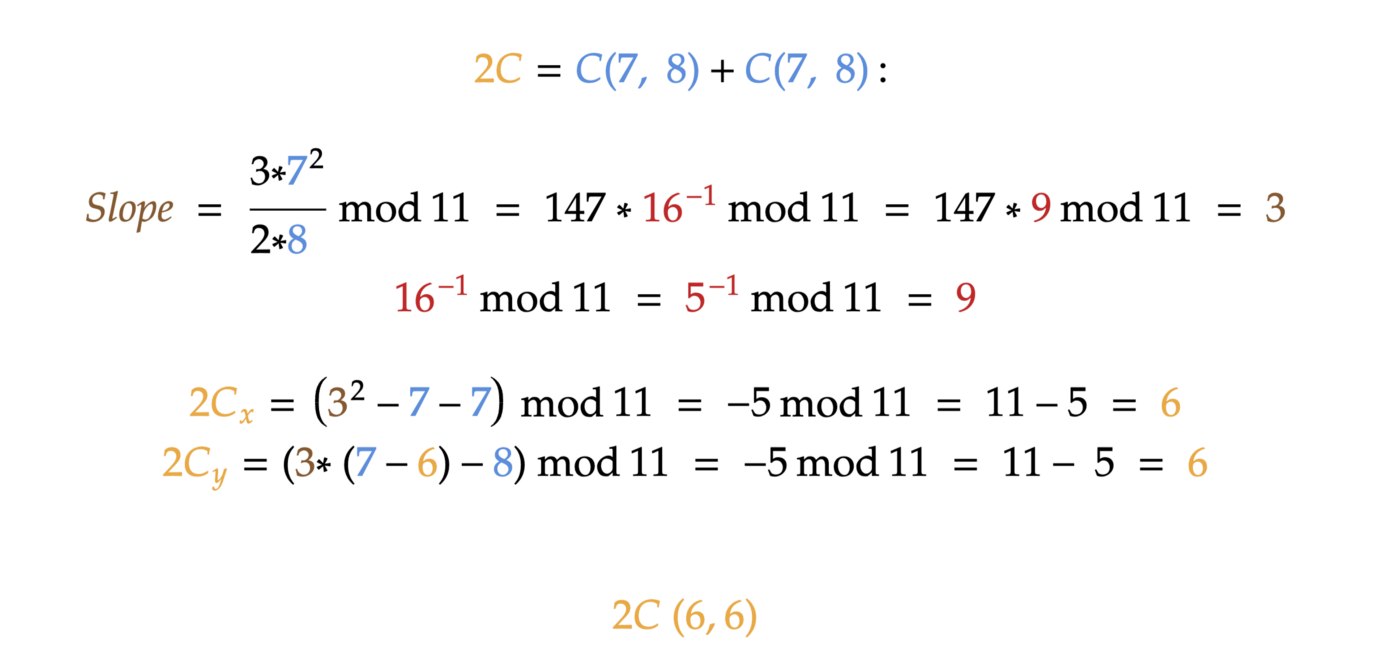
We can now easily calculate 4C:

Now let’s calculate 4C — C, which is essentially 3C = 4C + (-C):

Then let’s add 3C = C + 2C and see if the result is the same:

The math perfectly works here!
One super important property: Every point on a curve has its own order n! It works like a modulo. For example, if the order n of point C is 12, it means that 12C = 0 (the point doesn’t exist), 13C = C, 16C = 4C, 27C = 3C. This property is predefined for a point.
You can practice and make sure it works.
The order of our point C is actually 12. I suggest a task for you: try calculating 8C by adding 4C + 4C. Then try adding 8C + 8C. You will get 16C, which will be the same point as 4C.
It works like a clock:
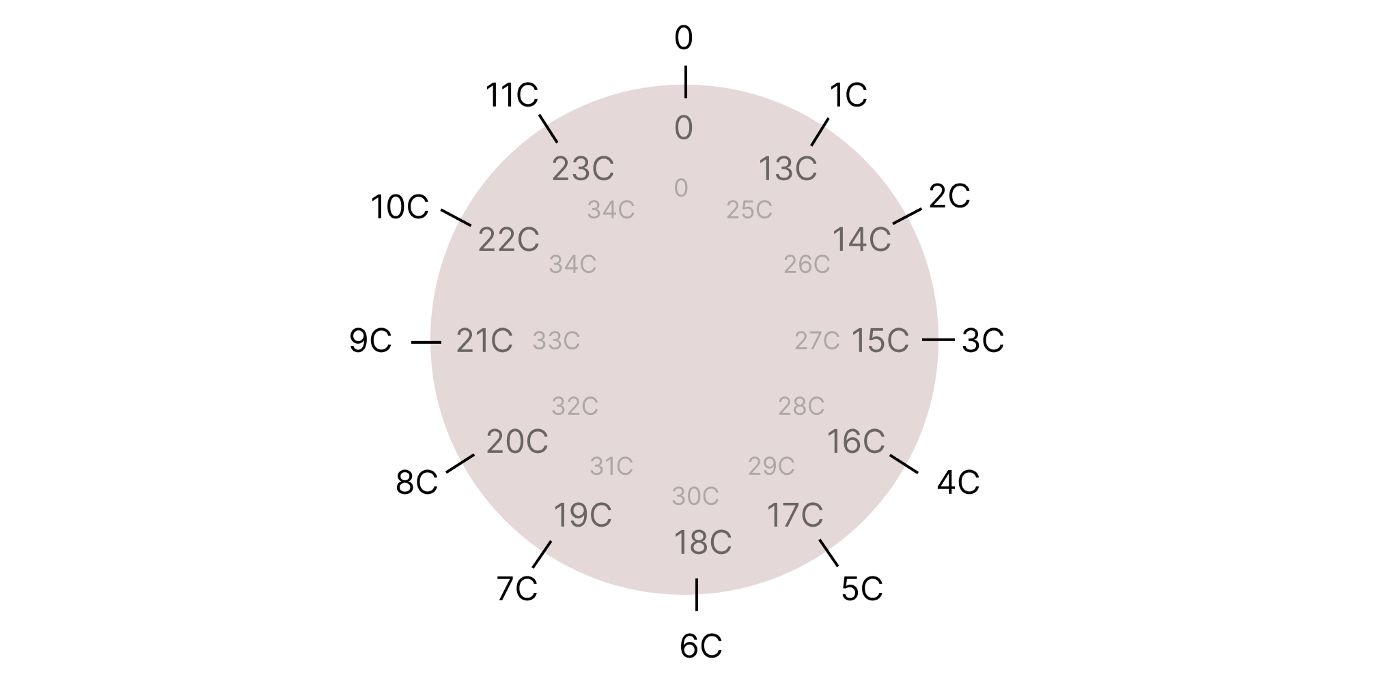
Now we know absolutely everything essential for using the elliptic curves in cryptography.
To recap
All formulas work fine. We can still calculate any integer x * Point. We still need approximately log2(x) operations!
Elliptic curves now have a finite set of points.
Points now have their own order n, so they tend to repeat themselves like in a clock.
To define an elliptic curve, we now need three variables: a, b, and p. p is called the order of an elliptic curve.
How do we know which a, b, and p to use? It’s standardized! There are many standards out there.
What do Bitcoin and Ethereum use?
They use the standardized elliptic curve called secp256k1. It has the following variables:
a=0
b=7
p=115792089237316195423570985008687907853269984665640564039457584007908834671663
Quite a big number! I think you’re starting to guess why elliptic curves are so good for cryptography.
Now that we know everything important, let’s apply it somewhere!
Part IV: Practical use of it: ECDSA
The Elliptic Curves Digital Signature Algorithm works exactly over the algebra that we’ve just discovered in the previous parts.
This algorithm allows a person to sign a message using their PrivateKey, so that anyone else can verify that the signature actually belongs to that person, also knowing their PublicKey.
This is what actually happens when you sign a message in blockchains:
You just generate some message like “I want to send X amount of crypto to address Y”, and then you sign that message (using exactly the algorithm discovered in this article). Other parties can verify that the message was actually signed by you.
How it works
Everything spins around one certain predefined point G, lying on a predefined elliptic curve.
We can generate any random integer and call it our PrivateKey.If we multiply this PrivateKey to point G, we will get the PublicKey. So PublicKey = PrivateKey * G:
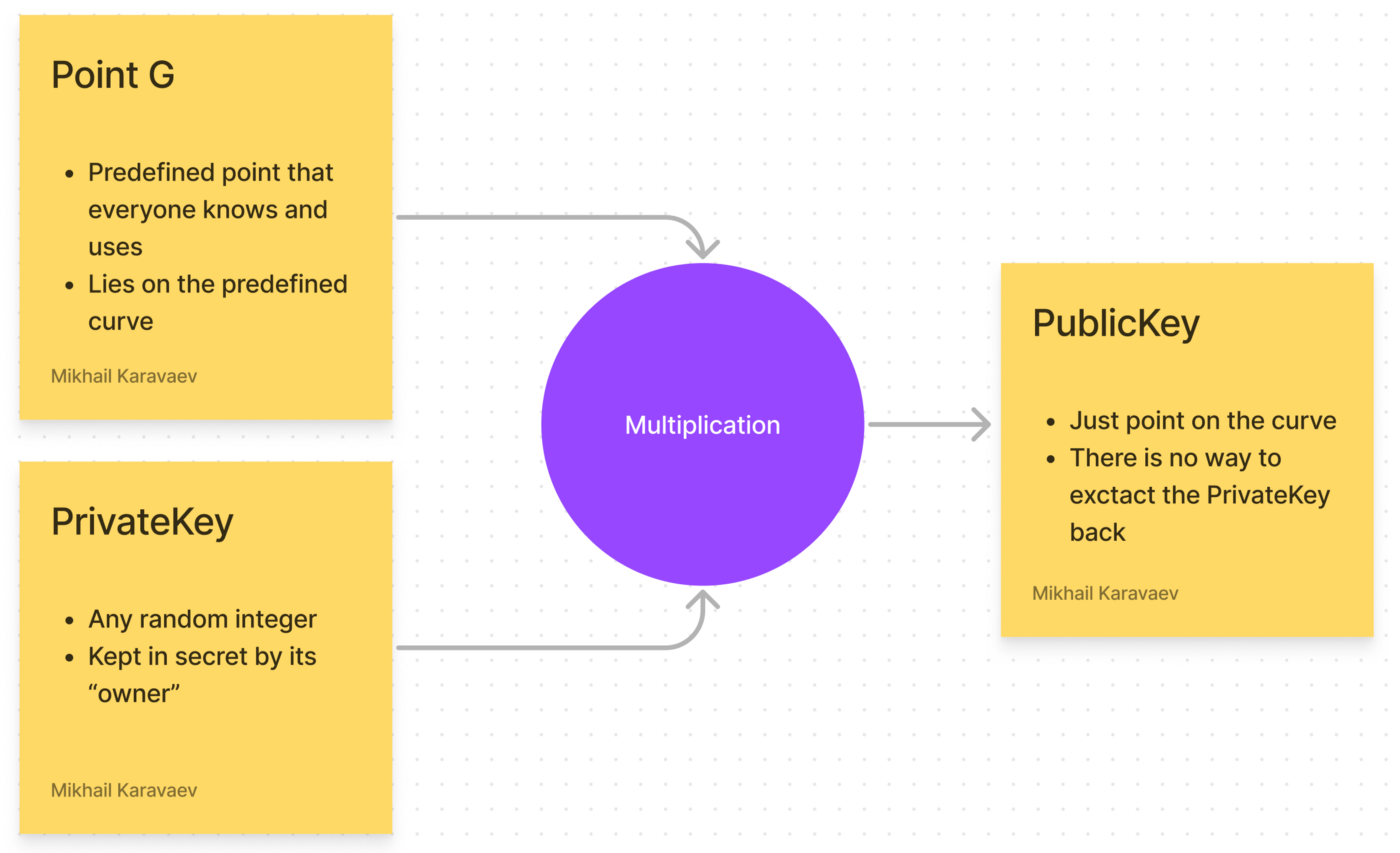
Yes, PublicKey is just a point on a curve.
As we already know, we can’t divide point by point or point by a scalar value. All possible operations are listed at the end of PART I.
So, there is no efficient way to extract PrivateKey from PublicKey, even though we know point G.
We can’t divide PublicKey by G. This operation doesn’t exist. Brute-forcing potentially works, but when there are really giant amount of possible points, for example, that giant:
115792089237316195423570985008687907852837564279074904382605163141518161494337
Even if someone uses all the existing computing power in the world, this will take billions of billions of billions… of years to find the PrivateKey.
In ECDSA, we have this set of “global” public variables. They are specified by standards:
Elliptic curve with some config (a, b, p)
Point G, which lies on the curve (its x and y coordinates). This is called the Generator Point. This point is standardized.
Order n of point G. As we know, order n is the property for point G, such as G*(n+1) = G, G*(n+2) = 2G, and so on.
Here are the variables that belong to a certain owner:
PrivateKey — kept secret by the owner
PublicKey — shared with the public
And variables that are specific to one signing operation:
The message itself: any integer that is not larger than order n. Usually, a hash of string is used. But for simplicity reasons, we will use pure integers.
K — random integer that is generated when signing a message, exactly for that signature. This is kept secret, and there is no way to find it by a third party.
Here is the complete picture. Green stickers indicate that the variable is shared with the public, and the red ones indicate the variables that are kept secret:
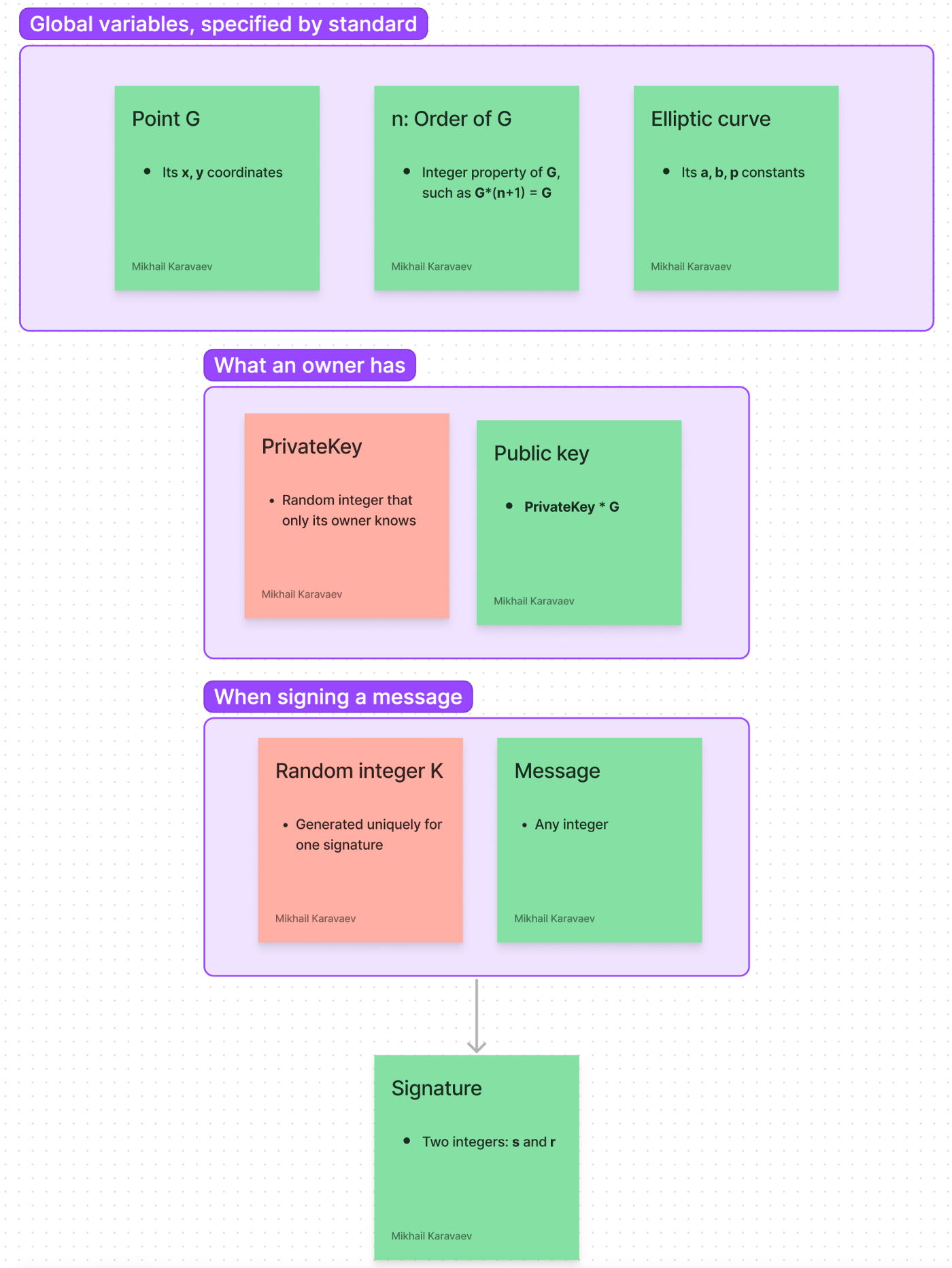
Way too many variables! Here are the algorithms for signing and verifying a message:
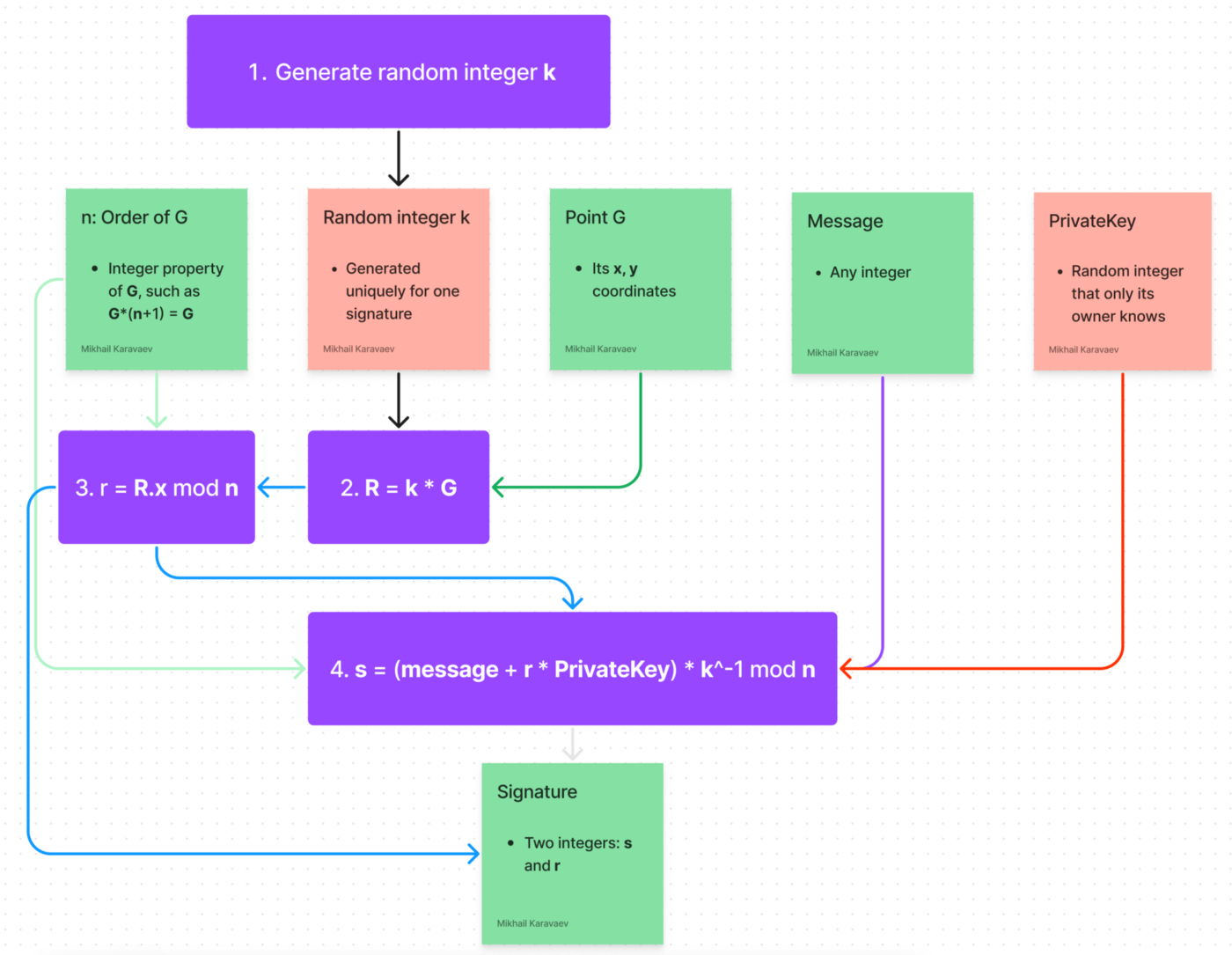
The algorithm for signing a message:
We have our PrivateKey and a message. To sign a message, we should:
Generate a random integer k. It should be a big number. [1, n-1]
Calculate point R = G * k
Calculate r:
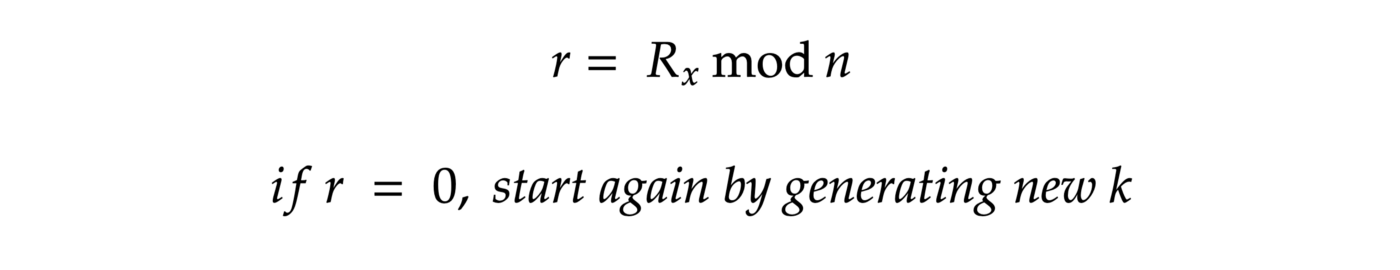
4. Calculate s:

That’s it. The signature is a pair of integers (r, s).
Here is the visual representation of the algorithm:
The algorithm for verifying a signature
We have the signer’s PublicKey, message, and signature(r, s).
Calculate U:
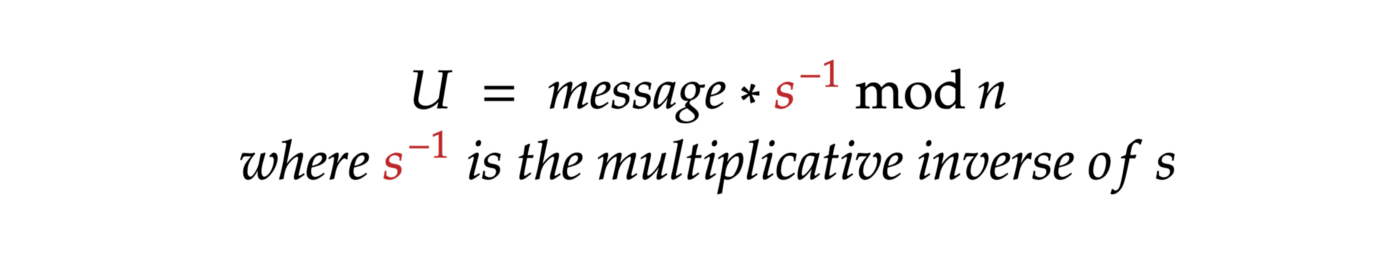
2. Calculate V:
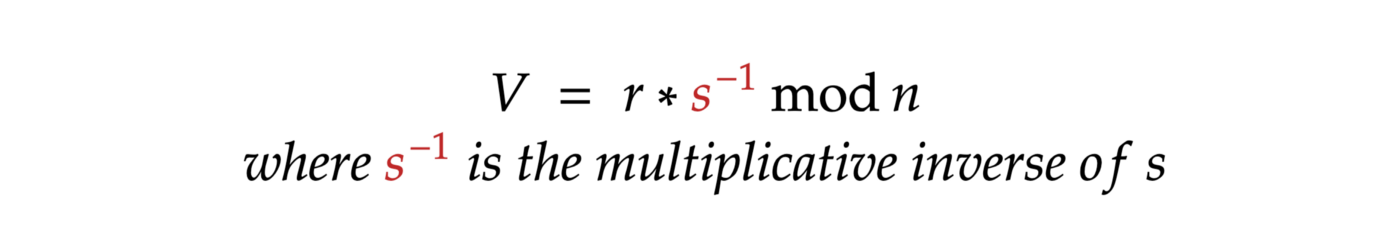
3. Calculate point C = U G + V PublicKey
4. If C.x mod n = r, then the signature is valid. Invalid otherwise.
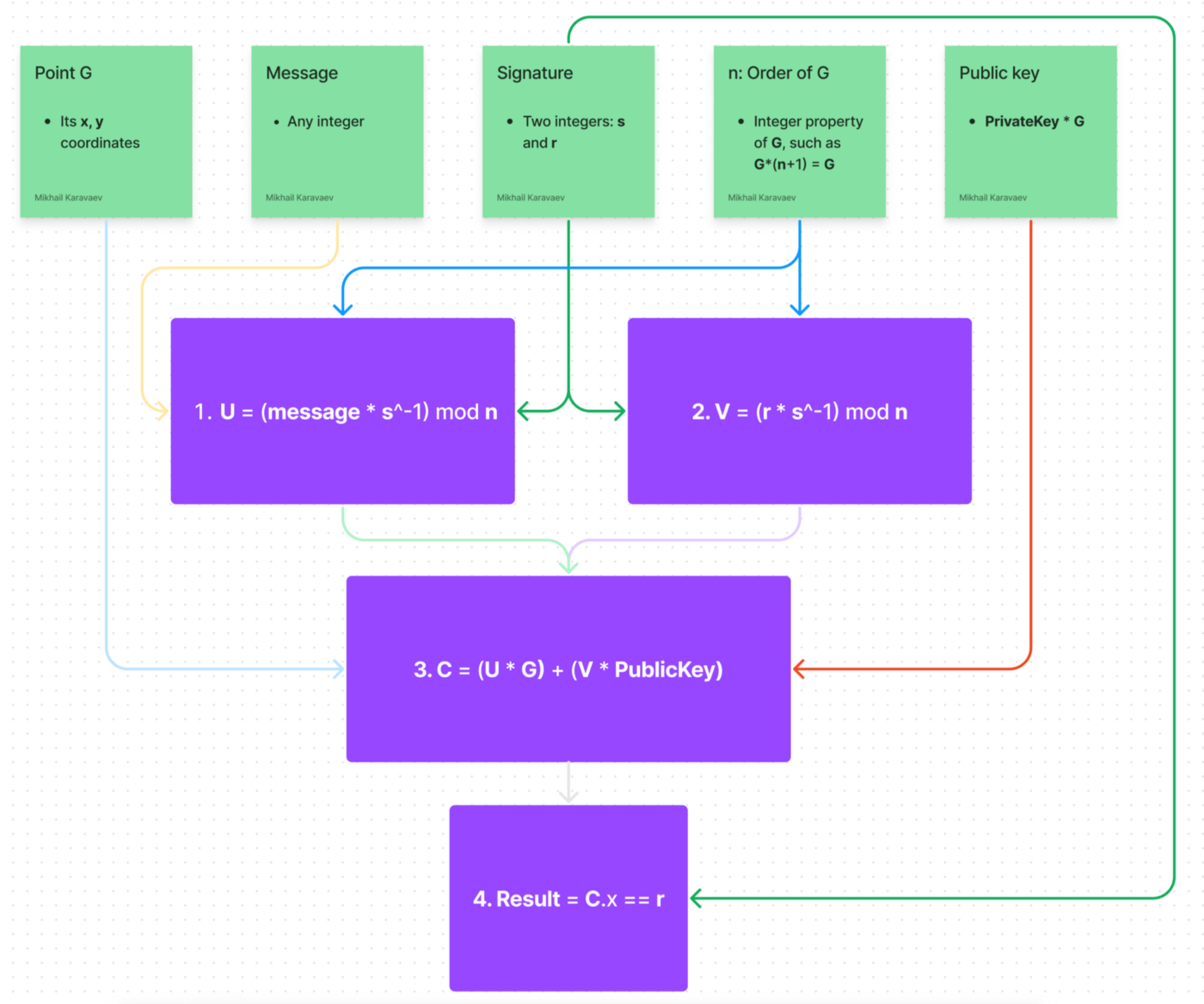
Not obvious at all!
Actually, this is just a mathematical trick.
Let’s play with our formulas and prove that it works!
In step 3 of our verification algorithm, we have a point
C = U * G + V * PublicKey:
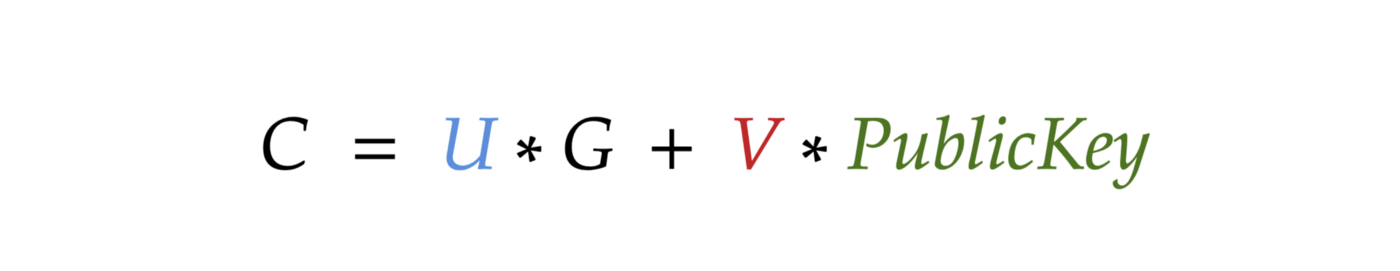
Let’s substitute the variables U, V, and PublicKey with their definitions:
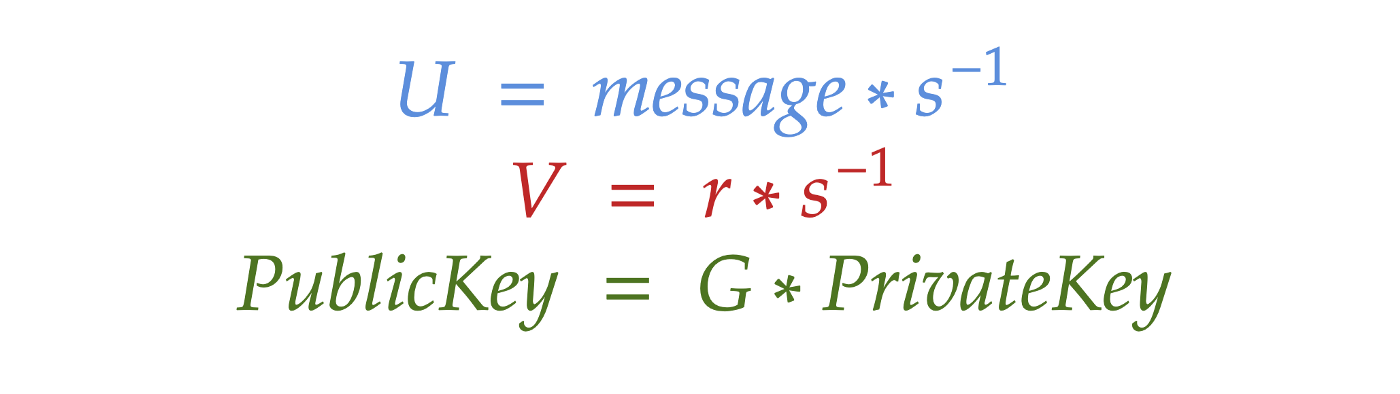
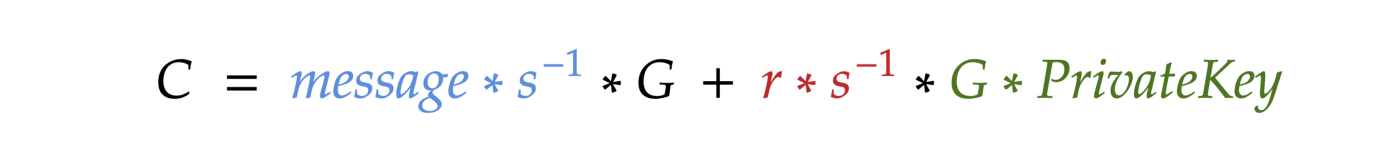
Notice that G * s^-1 is duplicated. Let’s simplify the formula:

Let’s see the definition of s in step 4 of the signing algorithm:
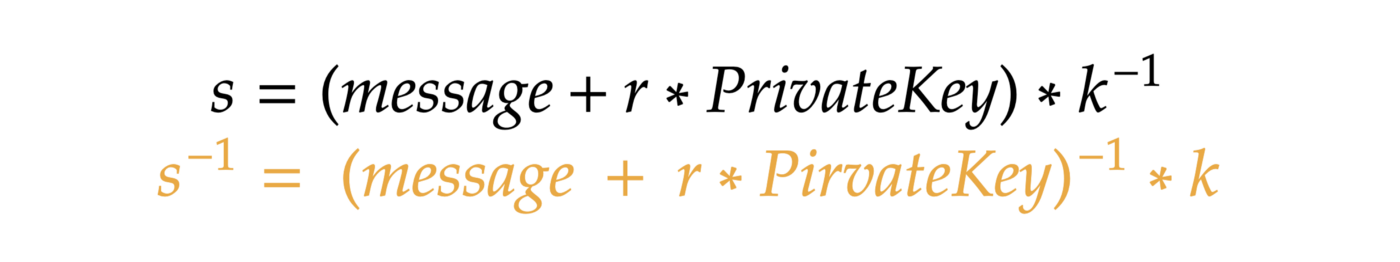
Let’s substitute s^-1 in our formula:

Let’s simplify this part:

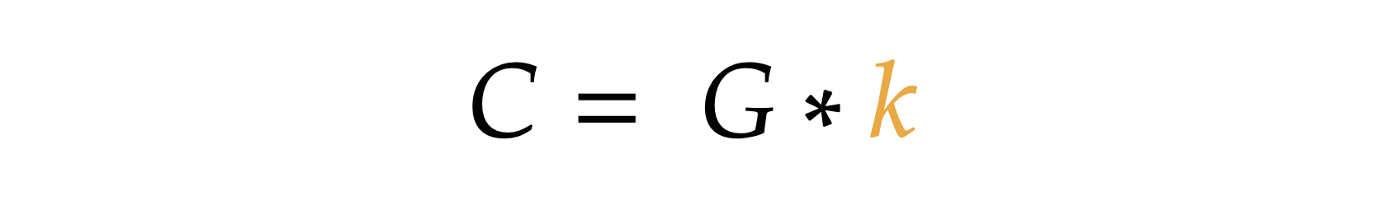
Thus, if the signature is correct, the x coordinate of C mod n is equal to r (which is, by its definition, the same x coordinate of G * k).
Secp256k1 standardized variables:
For the elliptic curve:
a=0
b=7
p=
115792089237316195423570985008687907853269984665640564039457584007908834671663
For point G:
x coordinate =
55066263022277343669578718895168534326250603453777594175500187360389116729240y coordinate =
32670510020758816978083085130507043184471273380659243275938904335757337482424Order n =
115792089237316195423570985008687907852837564279074904382605163141518161494337
Done! Now we know absolutely EVERYTHING essential!
The next part is going to be the easiest part for programmers. For everyone else, it’s not necessary to follow. Just proceed to the Live Demo.
Part V: The implementation
This part is intended for programmers.
The bottlenecks:
We need to be able to perform basic arithmetical operations on very large numbers. In programming, we can easily operate on large numbers using bignum arithmetic. So our programming language must support it, or we should use some external package to work with it. In the examples of this part, I will use Python, which supports bignum arithmetic out of the box. For the Live Demo (next part), I will use JavaScript, and there we will need the BigNumber.js package.
The other bottleneck that we will encounter is finding the multiplicative inverse of a huge number. Obviously, brute force is not going to work. The multiplicative inverse can be found by the Extended Euclidean algorithm, which has the complexity of O(log(n)).
Python (3.8+) can find the multiplicative inverse out of the box with its built-in pow function:
def find_inverse(number, modulus):
return pow(number, -1, modulus)If you need the actual implementation of the extended euclidean algorithm, check the code of my Live Demo!
Let’s start writing our code!
We need one simple thing related to the elliptic curve: Point. Let’s define a class Point. In its constructor, we should make check whether the point lies on the curve:
class Point:
def __init__(self, x, y, curve_config):
a = curve_config['a']
b = curve_config['b']
p = curve_config['p']
if (y ** 2) % p != (x ** 3 + a * x + b) % p:
raise Exception("The point is not on the curve")
self.x = x
self.y = y
self.curve_config = curve_configWe need to be able to compare two points, add them together, and multiply them by an integer.
Let’s add a method to check if two points are equal:
def is_equal_to(self, point):
return self.x == point.x & self.y == point.y
Now let’s implement add method, which returns a new Point as the result of addition:
def add(self, point):
p = self.curve_config['p']
if self.is_equal_to(point):
slope = (3 * point.x ** 2) * find_inverse(2 * point.y, p) % p
else:
slope = (point.y - self.y) * find_inverse(point.x - self.x, p) % p
x = (slope ** 2 - point.x - self.x) % p
y = (slope * (self.x - x) - self.y) % p
return Point(x, y, self.curve_config)
All the formulas are listed in PART III.
Now let’s implement the multiply method:
The most straightforward implementation would be this:
def multiply(self, times):
point = self
for i in range(times - 1):
point = point.add(self)
return point
But let’s say we need to multiply our point by a big number: 115792089237316195. Even if we had the speed of 1 billion additions per second, this would take 3.6 years to calculate this point!
And this is not even a big number for us! Here is a big number:
115792089237316195423570985008687907852837564279074904382605163141518161494337
Calculating the point in this way would take billions of billions of billions of billions… of years!
We can define that the efficiency of this algorithm above is O(n), which is of no use for our purposes. If you remember, there is an easy way to achieve O(log2(n)) complexity by continuously doubling our point:
2P = P+P
4P = 2P + 2P
8P = 4P + 4P
16P = 8P + 8P
32P= 16P + 16P
64P = 32P + 32P
And so log2(115792089237316195) = 56
log2(115792089237316195423570985008687907852837564279074904382605163141518161494337) = 256
So we don’t need billions of billions of billions… of years. We just need 256 operations to get to this large point!
Just one moment: to efficiently multiply by values that are not a degree of 2, it’s reasonable to store all the previous values, and then combine the results together.
For example, if we need to get 100P, we can no longer double 64P. Neither we can add points one by one: potentially this would take billions of billions of years on larger numbers. What’s reasonable to do instead, is:
96P = 64P + 32P
100P = 96P + 4P
So for that purpose, we need to store all the previous P’s and afterward efficiently use them.
So here is an efficient implementation:
def multiply(self, times):
current_point = self
current_coefficient = 1
pervious_points = []
while current_coefficient < times:
# store current point as a previous point
pervious_points.append((current_coefficient, current_point))
# if we can multiply our current point by 2, do it
if 2 * current_coefficient <= times:
current_point = current_point.add(current_point)
current_coefficient = 2 * current_coefficient
# if we can't multiply our current point by 2, let's find the biggest previous point to add to our point
else:
next_point = self
next_coefficient = 1
for (previous_coefficient, previous_point) in pervious_points:
if previous_coefficient + current_coefficient <= times:
if previous_point.x != current_point.x:
next_coefficient = previous_coefficient
next_point = previous_point
current_point = current_point.add(next_point)
current_coefficient = current_coefficient + next_coefficient
return current_point
Thus we’ve got a super efficient implementation! And now we can perform all the needed operations on an elliptic curve.
Let’s define secp256k1:
secp256k1_curve_config = {
'a': 0,
'b': 7,
'p': 115792089237316195423570985008687907853269984665640564039457584007908834671663
}
x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
n = 115792089237316195423570985008687907852837564279074904382605163141518161494337
g_point = Point(x, y, secp256k1_curve_config)
I’m using only decimal numbers in our examples because they’re intuitive for a human.
So far we’ve implemented everything that we discussed prior to PART IV. Now let’s implement the actual digital signature algorithm, described in PART IV.
Sign method of ECDSA:
def sign_message(message, private_key):
k = random.randint(1, n)
r_point = g_point.multiply(k)
r = r_point.x % n
if r == 0:
return sign_message(message, private_key)
k_inverse = find_inverse(k, n)
s = k_inverse * (message + r * private_key) % n
return r, s
Verify method of ECDSA:
def verify_signature(signature, message, public_key):
(r, s) = signature
s_inverse = find_inverse(s, n)
u = message * s_inverse % n
v = r * s_inverse % n
c_point = g_point.multiply(u).add(public_key.multiply(v))
return c_point.x == r
Let’s pick some random number as our private key, for example, 123456789012345.
Let our message be 12345.
Do you remember how to get PublicKey from PrivateKey?
private_key = 123456789012345 # any random integer
public_key = g_point.multiply(private_key)
message = 12345 # any integer
Now let’s sign and try to verify:
signature = sign_message(message, private_key)
print('Signature: ', signature)
print('Is valid: ', verify_signature(signature, message, public_key))
It works! You can try to corrupt the signature or the original message and make sure that our algorithm works properly.
Here is the complete code:
import random
def find_inverse(number, modulus):
return pow(number, -1, modulus)
class Point:
def __init__(self, x, y, curve_config):
a = curve_config['a']
b = curve_config['b']
p = curve_config['p']
if (y ** 2) % p != (x ** 3 + a * x + b) % p:
raise Exception("The point is not on the curve")
self.x = x
self.y = y
self.curve_config = curve_config
def is_equal_to(self, point):
return self.x == point.x and self.y == point.y
def add(self, point):
p = self.curve_config['p']
if self.is_equal_to(point):
slope = (3 * point.x ** 2) * find_inverse(2 * point.y, p) % p
else:
slope = (point.y - self.y) * find_inverse(point.x - self.x, p) % p
x = (slope ** 2 - point.x - self.x) % p
y = (slope * (self.x - x) - self.y) % p
return Point(x, y, self.curve_config)
def multiply(self, times):
current_point = self
current_coefficient = 1
pervious_points = []
while current_coefficient < times:
# store current point as a previous point
pervious_points.append((current_coefficient, current_point))
# if we can multiply our current point by 2, do it
if 2 * current_coefficient <= times:
current_point = current_point.add(current_point)
current_coefficient = 2 * current_coefficient
# if we can't multiply our current point by 2, let's find the biggest previous point to add to our point
else:
next_point = self
next_coefficient = 1
for (previous_coefficient, previous_point) in pervious_points:
if previous_coefficient + current_coefficient <= times:
if previous_point.x != current_point.x:
next_coefficient = previous_coefficient
next_point = previous_point
current_point = current_point.add(next_point)
current_coefficient = current_coefficient + next_coefficient
return current_point
secp256k1_curve_config = {
'a': 0,
'b': 7,
'p': 115792089237316195423570985008687907853269984665640564039457584007908834671663
}
x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
n = 115792089237316195423570985008687907852837564279074904382605163141518161494337
g_point = Point(x, y, secp256k1_curve_config)
def sign_message(message, private_key):
k = random.randint(1, n)
r_point = g_point.multiply(k)
r = r_point.x % n
if r == 0:
return sign_message(message, private_key)
k_inverse = find_inverse(k, n)
s = k_inverse * (message + r * private_key) % n
return r, s
def verify_signature(signature, message, public_key):
(r, s) = signature
s_inverse = find_inverse(s, n)
u = message * s_inverse % n
v = r * s_inverse % n
c_point = g_point.multiply(u).add(public_key.multiply(v))
return c_point.x == r
# test starts here
private_key = 123456789012345 # any random integer
public_key = g_point.multiply(private_key)
message = 12345 # any integer
signature = sign_message(message, private_key)
print('Signature: ', signature)
print('Is valid: ', verify_signature(signature, message, public_key))So the implementation of the entire ECDSA algorithm took just 100 lines of code! And it’s perfectly working. This is absolutely the same algorithm as the one used in Bitcoin!
PartVI: Live Demo
As I promised at the beginning of this article, here is the live demo using only the concepts and formulas described in the article. Just a couple of notes:
Initially, we could only sign integer messages. But in the demo, you can choose to apply a hash function (sha256) to your message. Thanks to it, a message can be a string.
Bitcoin uses slightly different formats of public keys and signatures.
Never use it in a production environment! It is not safe. For production, you must only use well-tested solutions.
I hope this article was very useful for you. I did my best to make it useful. Feel free to share it with friends or use any piece of it anywhere. Just please leave a link to the original article.
Feel free to contact me and ask questions:
Mikhail Karavaev