Фракталы, как правило, управляются довольно простыми правилами, порождая удивительную красоту. Однако я не встречал способов построения фракталов, основанных на простоте чисел. Фрактал, который получился у меня, быть может не так красив, как фрактал Мандельброта, и не содержит явного само-подобия (self-similarity), но также имеет бесконечно сложную структуру.

За 4 шага я покажу, как я его получил. Будет много картинок и мало формул.
Постоянные Фейгенбаума и теория хаоса

Многие уже узнали эту картинку, связанную с размножением кроликов. Пусть каждый год популяция кроликов увеличивается в a раз:
Если a, коэффициент размножения больше 1, то каждый год кроликов все больше и больше. В природе так не бывает. Пусть, если x приближается к 1, то кролики начинают умирать от болезней:
Дополнительная часть уравнения как раз отвечает за смертность кроликов, а картинка вверху показывает зависимость х (в пределе многих лет) от a. Как видно, при увеличении a до 3 равновесная плотность популяции растет, а потом мы видим неожиданное: происходит бифуркация: в один год кроликов меньше, в другой больше. Впрочем, мы такое поведение природы знаем по урожаю яблок, когда урожайные годы идут через один.
При дальнейшем увеличении a возникает вторая бифуркация, потом еще и еще, все чаще и чаще, а потом настает полный хаос. По мере приближения к хаосу время как бы ускоряется, плотность событий увеличивается. Предел отношений длин отрезков L является первой константой Фейгенбаума, 4.669... и она проявляет себя для очень широкого класса систем. Даже отношения размеров 'бубликов' (кардиоидов) у множества Мандельброта тоже 4.669.
Если за L0 (см. картинку вверху) взять промежуток времени 24 февраля - 21 сентября, то следующая бифуркация будет в первых числах ноября.
Фрактал Ляпунова
Фрактал назван в память о Ляпунове, который пустил себе пулю в голову за пол века до открытия фрактала, в котором используется экспонента Ляпунова. Идея генерации фрактала заключается в том, чтобы вместо одного значения a использовать два разных, a и b, и чередовать их по какому-нибудь правилу, например, abababab...:

начинаем мы с x=0.5, выбираем a и b (оси x и y), и вычисляем экспоненту Ляпунова. Для других последовательностей ab картинка будет выглядеть иначе, например для aabab:
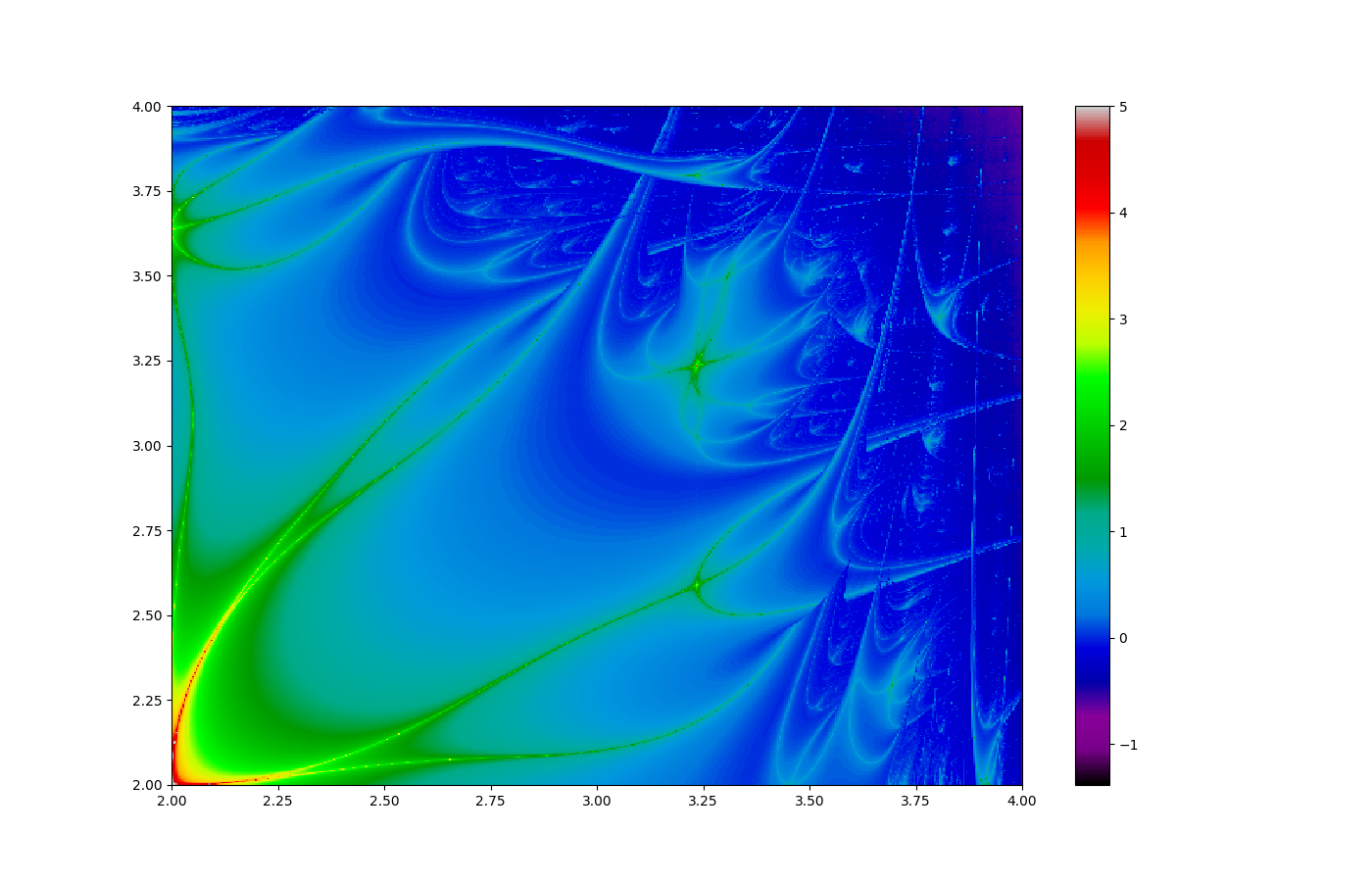
А теперь простые числа
Что если вместо периодической последовательности ab использовать апериодическую последовательность abbababaaa..., где a одначает что число составное, а b простое:
1-a, 2-простое, b, 3-простое b, 4- составное, a, 5 - b, 6-a, 7-b итд.

Картинка стала резко ассиметричной (что не удивительно, простых чисел меньше), но стала смазанной и менее интересной, на мой взгляд.
Кстати, а вы заметили, что оси у нас рисуются до значения 4? Это не случайно. При величине a>4 фрактал теряет устойчивость, значения улетают в бесконечность... Как и при отрисовке фрактала Мандельброта! Что если выкинуть экспоненту Ляпунова и отрисовывать (логарифм) количества итераций до того, как модуль x превысит некоторое значение, например, 1000?
Простые числа, вторая попытка
Теперь наши оси не ограничены значением 4:

Черный цвет означает стабильность - бесконечности не получается. Это наша знакомая область до 4. А вот дальше все интереснее/ Давайте увеличим район относительной стабильности около 4:
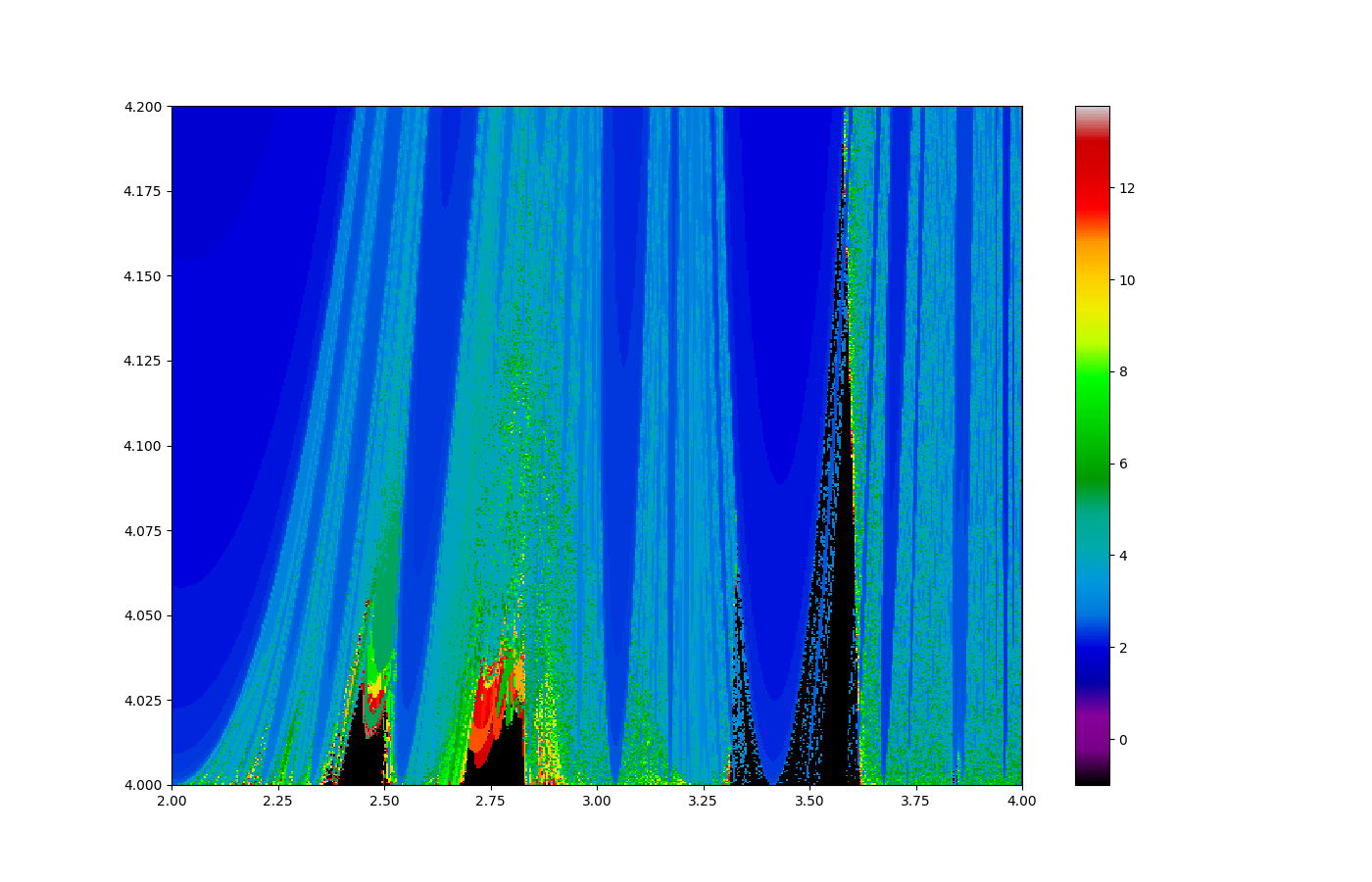
Картинка меняется довольно сильно, если 'объявить' число 3 или 5 составным, а вот большие числа (91, например) на картинку почти не влияют.
Еще один zoom:

И еще, кусочек справа:

'Прожектора', светящие в разные стороны, связаны с локальными сгущениями и разрежениями простых чисел. Просчитываются эти картинки довольно долго, 500x500 точек, для каждой надо скользить по простым числам до заданного предела (я брал 10-100 миллионов)