Задача теплопроводности методом продольно-поперечной прогонки средствами MPI / Habr

Приветствую.

Недавно в бэклоге появилась задача моделирования процесса теплопроводности. На осознание формулы и нахождения решения ушло немало времени и, чтобы у вас не возникали такие же трудности, хочу поделиться решением.

Постановка задачи

Задача теплопроводности - это задача математического моделирования.

На вход дается температура в исходном пространстве (сетке), а на выходе - температура через некоторое время.

Математическое представление следующее:

${\frac {\partial u}{\partial t}}-{\lambda}^{2}\left({\frac {\partial ^{2}u}{\partial x_{1}^{2}}}+{\frac {\partial ^{2}u}{\partial x_{2}^{2}}}+\cdots +{\frac {\partial ^{2}u}{\partial x_{n}^{2}}}\right)=f(x,t)$

где

- координаты в декартовом пространстве
${\partial t}$ - дельта времени
${\partial u}$ - изменения температуры в каждой точке
${\lambda}$ - коэффициент теплопроводности
- функция тепловых источников. В нашей задаче внутри сетки нет источников тепла, поэтому она равна 0 и акцентировать внимание на ней не будем.

Для текущей задачи с двумерной сеткой и отсутствием точек внутренних источников тепла функция будет выглядеть следующим образом

${\frac {\partial u}{\partial t}}-{\lambda}^{2}\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\right)=0$

Интерпретировать ее можно таким образом:

Изменение температуры на слое через какое-то количество времени равно сумме изменений температуры по каждому направлению с учетом коэффициента теплопроводности.

По факту мы имеем задачу Коши. Решение для нее существует, если даны граничные условия.

Граничные и начальные условия нам тоже даны

$x {\in}[0;1]\\y{\in}[0;0,5]$ $u(x, y, 0) = 300\\u(0, y, t)=600, u(1, y, t) = 1200\\u(x, 0, t)=600(1 + x), u(x, 0.5, t)=600(1 + x^3)$

Расшифровка условий

изменяется от 0 до 1

изменяется от 0 до 0.5

300 - начальная температура пространства

Температура при x = 0: 600, при x = 1: 1200

Температура при y = 0: 600(1 + x), при y = 0.5: 600(1 + x^3)

Но в формуле также присутствует и коэффициент теплопроводности. Для задачи он задается условием

${\lambda} = \begin{cases} 10^{-2}, x{\in}[0.25; 0.65], y{\in}[0.1;0.25] \\ 10^{-4} \end{cases}$

Продольно-поперечная прогонка

Существует множество готовых численных методов. Для решения будем использовать метод конечных разностей с неявной схемой.

Суть этого метода в последовательном нахождении температуры на следующем временном слое проходясь по всем направлениям поочередно. При прохождении по очередному слою мы находим состояние сетки в +1/n слое, где n - количество направлений.

Например, пусть нам дана 2-мерная сетка (X и Y), и ее состояние на 3 слое. Тогда:

Проходимся по X, находим состояние сетки в момент 3+½
Проходимся по Y, находим состояние в момент 4.

На этом итерация заканчивается

По аналогии с 3-мерной сеткой:

Проходимся по X, находим состояние 3+⅓
Проходимся по Y, находим состояние 3+⅔
Проходимся по Z, находим состояние 4

Метод прогонки

Метод прогонки - алгоритм решения систем линейных уравнений вида

где - трехдиагональная матрица вида

$M={\begin{pmatrix}C_{0}&B_{0}&0&0&\dots &0&0&0\\A_{1}&C_{1}&B_{1}&0&\dots &0&0&0\\0&A_{2}&C_{2}&B_{2}&\dots &0&0&0\\\dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\\dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\\dots &\dots &\dots &\dots &\dots &A_{n-1}&C_{n-1}&B_{n-1}\\0&0&0&0&\dots &0 &A_{n}&C_{n}\end{pmatrix}}$

Сама прогонка состоит из 2 этапов:

Прямая прогонка - нахождение коэффициентов ${\alpha}$ и ${\beta}$
Обратная прогонка - нахождение искомых значений

Метод состоит в следующем. Даны A, B, C - коэффициенты матрицы на каждой из строк и граничные условия - максимальное и минимальное значения на границах.

Прямая прогонка - находим коэффициенты ${\alpha}$ и ${\beta}$ . Коэффициенты находятся с помощью системы уравнений

${\displaystyle {\begin{cases}\alpha _{i}={\dfrac {-B_{i}}{A_{i}\alpha _{i-1}+C_{i}}}\\\beta _{i}={\dfrac {F_{i}-A_{i}\beta _{i-1}}{A_{i}\alpha _{i-1}+C_{i}}}\end{cases}}}\space ,\space\space i=1\dots N-1$

При этом ${\alpha}_0 = {\alpha_N} = 0$ , а значения ${\beta}_0$ и ${\beta}_N$ определяются из соответствующих краевых условий.

Для задачи теплопроводности ${\beta}_0 = min, {\beta}_N = max$ , где - температура в начале сетки, а - в конце для соответствующего направления. Например, если мы проходимся по направлению , то ,

Алгоритм работы такой:

Инициализируем начальные значения: ${\alpha}_0$ и ${\beta}_0$
Находим ${\alpha}_i$ и ${\beta}_i$ на основании ${\alpha}_{i-1}$ и ${\beta}_{i - 1}$

Обратная прогонка - находим исходные . Они находятся также при помощи формулы

$y_i={\alpha}_i y_{i + 1} + {\beta}_i \space,\space\space i=N-2\dots1\\y_N=max$

Алгоритм следующий:

Инициализируем начальное значение -
Находим на основании $y_{i + 1}$

Как можно заметить прямая прогонка - прогоночный коэффициент изменяется от 1 до , при обратной прогонке наоборот - от до 0.

Не забываем о матрице . Для удобства, представим матрицу в виде 3 других: . Где каждая матрица представляет свои коэффициенты.

В задаче теплопроводности их значения находятся через коэффициенты теплопроводности:

$A_{i,j} = - {\frac {\lambda_{i, j-1/2}} { 2h^2 }} \\ B_{i,j} = - {\frac {\lambda_{i, j+1/2}} { 2h^2 }} \\ C_{i, j} = {\frac 1 {\tau}} - A_{i,j} - B_{i, j}$

где

${\lambda}_{i,j{\pm}1/2} = {\frac {{\lambda}_{i,j{\pm}1} - {\lambda}_{i,j}} 2 }$ ${\lambda}_{i{\pm}1/2, j} = {\frac {{\lambda}_{i{\pm}1, j} - {\lambda}_{i,j}} 2 }$ - коэффициенты теплопроводности. Причем, первая используется при прогонке по направлению , а последнее - по
$\tau$ - шаг по времени. Задается нами. Например, 0.2
- шаг в пространстве. Например, если мы разбили направление x на 10 частей, то
$h={\frac {1 - 0} {10} }=0.1$

Теперь мы имеем все, чтобы сделать функцию решения задачи прогонки

void solveThomas(const double* F,
                    const double* lambda,
                    const int length,
                    const double min,
                    const double max,
                    const double step,
                    const double timeStep,
                    double* y) {
    const auto coefficient = 1.0 / (2 * step * step);

    double A[length], B[length], C[length];
    for (int i = 0; i < length; ++i) {
        A[i] = - avg(lambda[i + 1], lambda[i]) / 2 * coefficient;
        B[i] = - avg(lambda[i + 1], lambda[i + 2]) / 2 * coefficient;
        C[i] = 1 / timeStep - A[i] - B[i];
    }

    double alpha[length], beta[length];
    alpha[0] = alpha[length - 1] = 0;
    beta[0] = min;
    beta[length - 1] = max;

    for (int i = 0; i < length - 2; ++i) {
        alpha[i + 1] = - B[i + 1] / (C[i + 1] + A[i + 1] * alpha[i]);
        beta[i + 1] = (F[i + 1] - A[i + 1] * beta[i]) / (C[i + 1] + A[i + 1] * alpha[i]);
    }

    y[length - 1] = max;
    for (int i = length - 2; i >= 0; i--) {
        y[i] = alpha[i] * y[i + 1] + beta[i];
    }
}

Так как мы решаем задачу в одномерном случае, то матрицы представляем в виде массива, размером в длину сетки по текущему направлению.

Но у нас есть еще и , которое необходимо для нахождения на следующем слое. Для получения на следующем слое нам пригодятся следующие формулы

$\begin{cases} A_{i, j}y_{i-1, j}^{n + 1/2} + C_{i,j}y_{i, j}^{n + 1/2} + B_{i,j}y_{i + 1, j}^{n + 1/2} = F_{i, j}^{n},\space\space j=1 \dots, N_y - 1 \\ F_{i, j}^{n + 1/2} = {\frac {y_{i, j}^{n + 1/2}} {\tau} + {\frac {{\lambda}_{i+1/2, j}(y_{i+1, j}^{n+1/2} - y_{i, j}^{n+1/2}) - {\lambda}_{i-1/2, j}(y_{i, j}^{n+1/2} - y_{i-1, j}^{n+1/2})} {2h_x^2} }} \end{cases} \\ \begin{cases} A_{i, j}y_{i, j-1}^{n + 1} + C_{i,j}y_{i, j}^{n + 1} + B_{i,j}y_{i, j+1}^{n + 1} = F_{i, j}^{n + 1/2},\space\space i=1 \dots, N _x- 1 \\ F_{i, j}^{n} = {\frac {y_{i, j}^{n}} {\tau} + {\frac {{\lambda}_{i, j+1/2}(y_{i, j+1}^n - y_{i, j}^n) - {\lambda}_{i, j-1/2}(y_{i, j}^n - y_{i, j-1}^n)} {2h_y^2} }} \end{cases}$

где

- количество разбиений по направлению X
- количество разбиений по направлению Y
Верхние коэффициенты - временной слой

Объяснение формул

Первая скобка рассказывает как делать итерацию по :

Делаем прогонку по направлению и находим $y^{n+1/2}$
Вычисляем $F^{n+1/2}$ - значения на n+1/2 слое

Вторая скобка рассказываем как делать итерацию по Y:

Делаем прогонку по направлению и находим $y^{n+1}$
Вычисляем $F^{n+1}$ - значения на n+1 слое (n можно заменить на n+1)

Заметим, что при вычислении на каком-либо направлении мы зависим, только от тех , которые нашли для направления при соответствующих коэффициентах прогонки. Грубо говоря, чтобы получить значения на соответствующем слое $(F^{n + 1/2}, F^{n + 1})$ нам требуются только те , которые мы нашли из проведенной прогонки на слое. Если мы делали прогонку по с и нашли значения $y_{1, j}^{n + 1/2}$ , то для нахождения $F_{1, j}^{n+1/2}$ необходимы только $y_{1, j}^{n + 1/2}$

Теперь мы можем написать функцию для восстановления значений по данным

void restoreF(const double* y,
              const double* lambda,
              const int size,
              const double step,
              const double timeStep,
              double* F) {
    const double coefficient = 1 / (2 * step * step);
    for (int i = 1; i < size - 1; ++i) {
        double lambdaPlusHalf = avg(lambda[i], lambda[i + 1]);
        double lambdaMinusHalf = avg(lambda[i], lambda[i - 1]);
        double temp = lambdaPlusHalf * (y[i + 1] - y[i]) - lambdaMinusHalf * (y[i] - y[i - 1]);
        F[i] = y[i] / timeStep + temp * coefficient;
    }
}

Последовательное решение

Теперь мы можем решить задачу в 2-мерном случае. Все что нам осталось сделать - инициализировать начальные данные и правильно оформить логику прогонки: обернуть итерации в циклы в правильной последовательности.

double getLambda(double x, double y) {
    return 0.25 <= x && x <= 0.65 &&
    0.1 <= y && y <= 0.25 ? 0.01 : 0.0001;
}

double avg(double left, double right) {
    return (left + right) / 2;
}

void solveThomas(const double* F,
                    const double* lambda,
                    const int length,
                    const double min,
                    const double max,
                    const double step,
                    const double timeStep,
                    double* y) {
    const auto coefficient = 1.0 / (2 * step * step);

    double A[length], B[length], C[length];
    for (int i = 0; i < length; ++i) {
        A[i] = - avg(lambda[i + 1], lambda[i]) / 2 * coefficient;
        B[i] = - avg(lambda[i + 1], lambda[i + 2]) / 2 * coefficient;
        C[i] = 1 / timeStep - A[i] - B[i];
    }

    double alpha[length], beta[length];
    alpha[0] = alpha[length - 1] = 0;
    beta[0] = min;
    beta[length - 1] = max;

    for (int i = 0; i < length - 2; ++i) {
        alpha[i + 1] = - B[i + 1] / (C[i + 1] + A[i + 1] * alpha[i]);
        beta[i + 1] = (F[i + 1] - A[i + 1] * beta[i]) / (C[i + 1] + A[i + 1] * alpha[i]);
    }

    y[length - 1] = max;
    for (int i = length - 2; i >= 0; i--) {
        y[i] = alpha[i] * y[i + 1] + beta[i];
    }
}

void restoreF(const double* y,
              const double* lambda,
              const int size,
              const double step,
              const double timeStep,
              double* F) {
    const double coefficient = 1 / (2 * step * step);
    for (int i = 1; i < size - 1; ++i) {
        double lambdaPlusHalf = avg(lambda[i], lambda[i + 1]);
        double lambdaMinusHalf = avg(lambda[i], lambda[i - 1]);
        double temp = lambdaPlusHalf * (y[i + 1] - y[i]) - lambdaMinusHalf * (y[i] - y[i - 1]);
        F[i] = y[i] / timeStep + temp * coefficient;
    }
}

int main(int argc, char** argv) {
    const int size = 10;
    const double timeStep = 0.1;
    const double tLeft = 600;
    const double tRight = 1200;
    const double xMin = 0;
    const double xMax = 1;
    const double yMin = 0;
    const double yMax = 0.5;
    const double xStep = (xMax - xMin) / size;
    const double yStep = (yMax - yMin) / size;

    // y - исходная температура
    double temperatureByX[size][size];
    double lambdaByX[size][size];
    // F
    double FByX[size][size];
    for (int i = 0; i < size; ++i) {
        auto x = i * xStep;
        for (int j = 0; j < size; ++j) {
            auto y = j * yStep;
            lambdaByX[i][j] = getLambda(x, y);
            temperatureByX[i][j] = 300;
            FByX[i][j] = 0;
        }
    }

    for (int i = 0; i < size; ++i) {
        restoreF(temperatureByX[i], lambdaByX[i], size, xStep, timeStep, FByX[i]);
    }

    // Меняю строки и столбцы
    double temperatureByY[size][size];
    double FByY[size][size];
    double lambdaByY[size][size];

    for (int y = 0; y < size; ++y) {
        for (int x = 0; x < size; ++x) {
            temperatureByY[y][x] = temperatureByX[x][y];
            FByY[y][x] = FByX[x][y];
            lambdaByY[y][x] = lambdaByX[x][y];
        }
    }


    const int iterations = 100;
    for (int t = 0; t < iterations; ++t) {
        // Вычисляю yn+1/2
        for (int x = 0; x < size; ++x) {
            solveThomas(FByX[x], lambdaByX[x], size, tLeft, tRight, xStep, timeStep, temperatureByX[x]);
        }

        // Вычисляю Fn+1/2
        for (int x = 0; x < size; ++x) {
            restoreF(temperatureByX[x], lambdaByX[x], size, xStep, timeStep, FByX[x]);
        }

        // Обновляю значения температуры и F по Y
        for (int y = 0; y < size; ++y) {
            for (int x = 0; x < size; ++x) {
                FByY[y][x] = FByX[x][y];
            }
        }

        // Вычисляю yn+1
        for (int y = 0; y < size; ++y) {
            double x = xMin + y * xStep;
            solveThomas(FByY[y], lambdaByY[y], size, 600 * (1 + x), 600 * (1 + x * x * x), yStep, timeStep, temperatureByY[y]);
        }

        // Вычисляю Fn+1
        for (int y = 0; y < size; ++y) {
            restoreF(temperatureByY[y], lambdaByY[y], size, yStep, timeStep, FByY[y]);
        }


        // Обновляю значения температуры и F по X
        for (int x = 0; x < size; ++x) {
            for (int y = 0; y < size; ++y) {
                temperatureByX[x][y] = temperatureByY[y][x];
                FByX[x][y] = FByY[y][x];
            }
        }
    }

}

Параллельная реализация

Можно заметить, что при прогонке по каждому направлению, значения независят друг от друга. Например, при прогонке по X, строки 1 и 2 не зависят друг от друга. Это хорошая точка для распараллеливания.

Данная задача - CPU-bound. Для них подходит распараллеливание по процессам. Будем использовать MPI - интерфейс для обмена сообщениями между процессами. Познакомиться с ним можно здесь.

Функции для распараллеливания

Все что нам нужно - передать массивы и по нужным направлениям. Для передачи массивов данных по всем направлениям существует функция MPI_Scatter

int MPI_Scatter(const void *sendbuf, int sendcount, MPI_Datatype sendtype, 
                void *recvbuf, int recvcount, MPI_Datatype recvtype, 
                int root, MPI_Comm comm)

Она передает массивы фиксированной длины на все процессы, включая отправитель. Но мало передать, нужно и получить обратно. Для этого тоже есть функция - MPI_Gather

int MPI_Gather(const void *sendbuf, int sendcount, MPI_Datatype sendtype, 
               void *recvbuf, int recvcount, MPI_Datatype recvtype, 
               int root, MPI_Comm comm)

Она собирает массивы фиксированного размера со всех процессов, включая корень.

В итоге, итерация будет выглядеть следующим образом:

Передаем данные по направлению X по процессам
Находим температуру
Находим F
Возвращаем посчитанные данные на главный процесс
Обновляем значения температуры и F
Передаем данные по направлению X по процессам
Находим температуру
Находим F
Возвращаем посчитанные данные на главный процесс
Обновляем данные температуры и F

Вспомогательные детали

Для удобства, размеры сетки в обе стороны одинаковые. Поэтому количество процессов сделаем равным размеру сетки в одном направлении. Проверка при старте приложения.

int processesCount;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &processesCount);
if (processesCount != size) {
    if (rank == 0) {
        std::cout << "Количество процессов должно быть " << size << std::endl;
    }
    MPI_Finalize();
    return 0;
}

Для более удобного логического представления программы сделаем ветвление по номеру процесса: мастер попадет в свою секцию, слейвы попадут в свою.

int rank;
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
if (rank == 0) {
  // Работа главного процесса
} else {
  // Работа слейвов
}

Свой тип данных для колоночной передачи матрицы

В нашей предыдущей реализации мы использовали 2 типа массивов для хранения: по X и по Y, а при слиянии результатов меняли их местами. Это не совсем эффективно, т.к. размер матрицы растет экспоненциально. Было бы неплохо передавать матрицу по столбцам и по строкам без необходимости каких-либо манипуляций. Решение - свой тип данных.

В MPI свой тип данных можно создать с помощью функции MPI_Type_vector

int MPI_Type_vector(int count, int blocklength, int stride, 
                    MPI_Datatype oldtype,
                    MPI_Datatype *newtype)

Логическое представление влияния передаваемых аргументов функции MPI_Type_vector

Для передачи матрицы по столбцам создим новый тип данных таким способом:

// size - размер матрицы в одном направлении
MPI_Datatype matrixColumnsType;
// Всего у нас size столбцов, 
// в каждом из которых нужно взять 1 число 
// из блока в size чисел
// типа double (MPI_DOUBLE)
MPI_Type_vector(size, 1, size, MPI_DOUBLE, &matrixColumnsType);
MPI_Type_commit(&matrixColumnsType);

Но есть проблема. Если использовать созданый тип данных при передаче, то первый столбец передастся удачно, а дальше произойдет выход за границы массива. Дело в том, что MPI_Type_vector не учитывает смещение при индексировании. Грубо говоря, сейчас, когда мы передали первый столбец, переход ко второму начинается не смещением на sizeof(double), а на весь размер созданного типа данных, а это size (count) * size (stride) - начинаем передачу с конца массива матрицы.

Чтобы это исправить есть другая функция - MPI_Type_create_resized

int MPI_Type_create_resized(MPI_Datatype oldtype, 
                            MPI_Aint lb, 
                            MPI_Aint extent,
                            MPI_Datatype *newtype)

Она создает новый тип данных из исходного, но изменяет дельту при перемещении к следующему элементу. Чтобы исправить найденный недочет, создадим новый тип данных

MPI_Datatype columnType;
MPI_Type_create_resized(matrixColumnsType, 0, sizeof(double), &columnType);
MPI_Type_commit(&columnType);

Итоговая программа

#include <iostream>
#include <mpi.h>

double getLambda(double x, double y) {
    return 0.25 <= x && x <= 0.65 &&
    0.1 <= y && y <= 0.25 ? 0.01 : 0.0001;
}

double avg(double left, double right) {
    return (left + right) / 2;
}

void solveThomas(const double* F,
                    const double* lambda,
                    const int length,
                    const double min,
                    const double max,
                    const double step,
                    const double timeStep,
                    double* y) {
    const auto coefficient = 1.0 / (2 * step * step);

    double A[length], B[length], C[length];
    for (int i = 0; i < length; ++i) {
        A[i] = - avg(lambda[i + 1], lambda[i]) / 2 * coefficient;
        B[i] = - avg(lambda[i + 1], lambda[i + 2]) / 2 * coefficient;
        C[i] = 1 / timeStep - A[i] - B[i];
    }

    double alpha[length], beta[length];
    alpha[0] = alpha[length - 1] = 0;
    beta[0] = min;
    beta[length - 1] = max;

    for (int i = 0; i < length - 2; ++i) {
        alpha[i + 1] = - B[i + 1] / (C[i + 1] + A[i + 1] * alpha[i]);
        beta[i + 1] = (F[i + 1] - A[i + 1] * beta[i]) / (C[i + 1] + A[i + 1] * alpha[i]);
    }

    y[length - 1] = max;
    for (int i = length - 2; i >= 0; i--) {
        y[i] = alpha[i] * y[i + 1] + beta[i];
    }
}

void restoreF(const double* y,
              const double* lambda,
              const int size,
              const double step,
              const double timeStep,
              double* F) {
    const double coefficient = 1 / (2 * step * step);
    for (int i = 1; i < size - 1; ++i) {
        double lambdaPlusHalf = avg(lambda[i], lambda[i + 1]);
        double lambdaMinusHalf = avg(lambda[i], lambda[i - 1]);
        double temp = lambdaPlusHalf * (y[i + 1] - y[i]) - lambdaMinusHalf * (y[i] - y[i - 1]);
        F[i] = y[i] / timeStep + temp * coefficient;
    }
}

int main(int argc, char** argv) {
    const int size = 30;
    const int iterations = 3000;
    const double timeStep = 0.2;
    const double TxLeft = 600;
    const double TxRight = 1200;
    const double xStart = 0;
    const double xEnd = 1;
    const double yStart = 0;
    const double yEnd = 0.5;
    const double xStep = (xEnd - xStart) / size;
    const double yStep = (yEnd - yStart) / size;

    int processesCount, rank;
    
    double lambdaByX[size][size];
    double lambdaByY[size][size];

    for (int i = 0; i < size; ++i) {
        const double xValue = xStart + i * xStep;
        for (int j = 0; j < size; ++j) {
            const double yValue = yStart + j * yStep;
            double lambda = getLambda(xValue, yValue);
            lambdaByX[i][j] = lambda;
            lambdaByY[j][i] = lambda;
        }
    }

    MPI_Init(&argc, &argv);
    MPI_Comm_size(MPI_COMM_WORLD, &processesCount);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    if (processesCount != size) {
        if (rank == 0) {
            std::cout << "Количество процессов должно быть " << size << std::endl;
        }
        MPI_Finalize();
        return 0;
    }

    /// Создаем свой тип данных для передачи по столбцам
    MPI_Datatype matrixColumnsType, columnType;

    // Передача по столбцам
    MPI_Type_vector(size, 1, size, MPI_DOUBLE, &matrixColumnsType);
    MPI_Type_commit(&matrixColumnsType);

    // Перемещение по массиву делаем через каждые sizeof(double) байтов, т.е. смещение в 1 элемент
    MPI_Type_create_resized(matrixColumnsType, 0, sizeof(double), &columnType);
    MPI_Type_commit(&columnType);

    double* myLambdaX = lambdaByX[rank];
    double* myLambdaY = lambdaByY[rank];

    double temperatureReceive[size];
    double fReceive[size];

    if (rank == 0) {
        double temperature[size * size];
        double F[size * size];

        // Инициализируем начальные значения
        for (int i = 0; i < size; ++i) {
            for (int j = 0; j < size; ++j) {
                temperature[i * size + j] = 300;
                F[i * size + j] = 0;
            }
        }

        // Восстанавливаем первое значение F (F0)
        // Не по формуле - идем в другую сторону (восстанавливаем по X, а не по Y)
        for (int i = 0; i < size; ++i) {
            restoreF((temperature + i * size), lambdaByX[i], size, xStep, timeStep, (F + i * size));
        }

        for (int t = 0; t < iterations; ++t) {
            /// Вычисляю yn+1/2 и Fn+1/2
            MPI_Scatter(F, size, MPI_DOUBLE,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            solveThomas(fReceive, myLambdaX, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaX, size, xStep, timeStep, fReceive);

            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       temperature, 1, columnType,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       F, 1, columnType,
                       0, MPI_COMM_WORLD);


            /// Вычисляю yn+1 и Fn+1
            MPI_Scatter(temperature, 1, columnType,
                        temperatureReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);
            MPI_Scatter(F, 1, columnType,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            solveThomas(fReceive, myLambdaX, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaX, size, xStep, timeStep, fReceive);

            // Аналогично принимаем только 1 элемент
            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       temperature, 1, columnType,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       F, 1, columnType,
                       0, MPI_COMM_WORLD);
        }
      
        for (int i = 1; i < size - 1; ++i) {
          for (int j = 1; j < size - 1; ++j) {
              std::cout << temperature[i * size + j] << " ";
          }
          std::cout << "\n";
        }
      } else {
        for (int t = 0; t < iterations; ++t) {

            /// Вычисляю yn+1/2 и Fn+1/2
            // Получаю значения fReceive по X
            MPI_Scatter(fReceive, size, MPI_DOUBLE,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            // Само вычисление
            solveThomas(fReceive, myLambdaX, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaX, size, xStep, timeStep, fReceive);

            // Возвращаю полученные данные
            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);

            /// Вычисляю yn+1 и Fn+1
            // Получаю значения температуры и fReceive по Y
            MPI_Scatter(nullptr, 0, MPI_DOUBLE,
                        temperatureReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);
            MPI_Scatter(nullptr, 0, MPI_DOUBLE,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            // Само вычисление
            solveThomas(fReceive, myLambdaY, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaY, size, xStep, timeStep, fReceive);

            // Возвращаю полученные значения
            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);
        }
    }

    MPI_Type_free(&columnType);
    MPI_Type_free(&matrixColumnsType);

    MPI_Finalize();

}

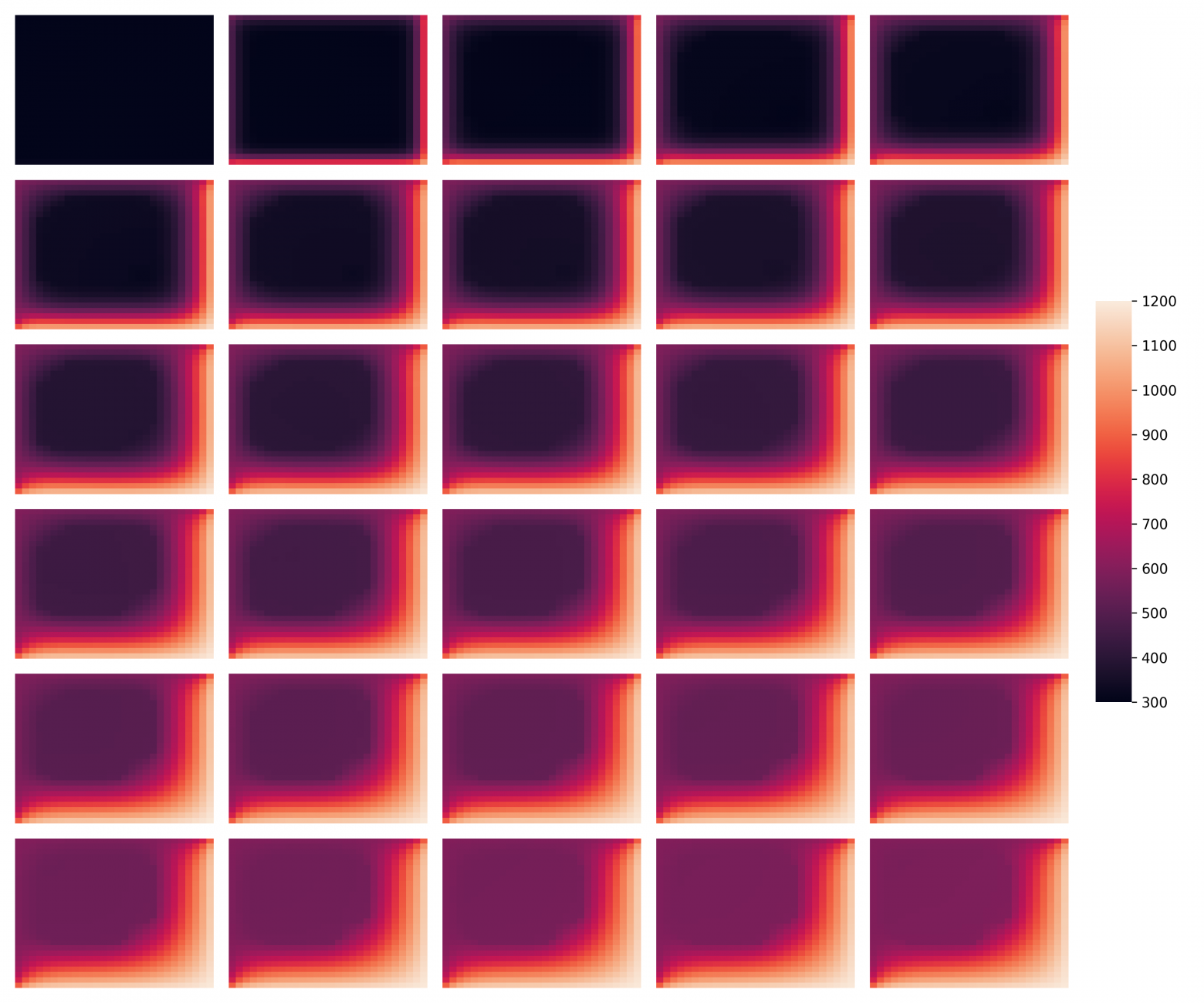
Визуализация

Для визуализации логировались каждые 100 шагов из 3000 итераций с шагом 0.2. Результаты визуализированы с помощью matplotlib и seaborn

Полезные ссылки

https://ru.wikipedia.org/wiki/Уравнение_теплопроводности - Теория по задаче теплопроводности
https://algowiki-project.org/ru/Алгоритм_продольно-поперечной_прогонки - Объяснение алгоритма продольно-поперечной прогонки
https://github.com/ashenBlade/adi-mpi - Репозиторий с исходным кодом
https://stackoverflow.com/questions/10788180/sending-columns-of-a-matrix-using-mpi-scatter - Вопрос, который помог создать тип для отправки матрицы по столбцам