В 1982 годy американские студенты, сдававшие SAT тест (аналог ЕГ) должны были ответить на простой вопрос. Звучал он следующим образом:

Радиус окружности a в три раза больше чем радиус окружности b. Начиная с позиции, показанной на изображении, окружность b катится вокруг окружности a. К моменту когда окружность b вернется в начальную позицию, как много оборотов она совершит?
Варианты ответов:
а) 3/2
b) 3
c) 6
d) 9/2
e) 9
Вы ведь уже догадались что вопрос с подвохом? Тогда внимательно следите за движением точки H' и считайте обороты!

Итак, если вы выбрали вариант "b) 3" то сейчас я вам докажу что вы ошиблись. А если вы решили схитрить и выбрали вариант "a) 3/2", "c) 6", "d) 9/2" или "e) 9" то вы все равно ошиблись!
Давайте проследим за траекторией центра окружности b - точкой B. Она представляет собой окружность с радиусом:

В таком случает длина траектории точки B это:
Получается что нужно 4 оборота окружности b чтобы точка B вернулась в свое первоначальное положение!
Так чему вы же больше верите: своим глазам или математическим расчетам?
Тогда попробуйте посчитать количество оборотов еще раз. На этот раз я добавил на рисунок оси, привязав их к центру окружности b, чтобы вам было проще.
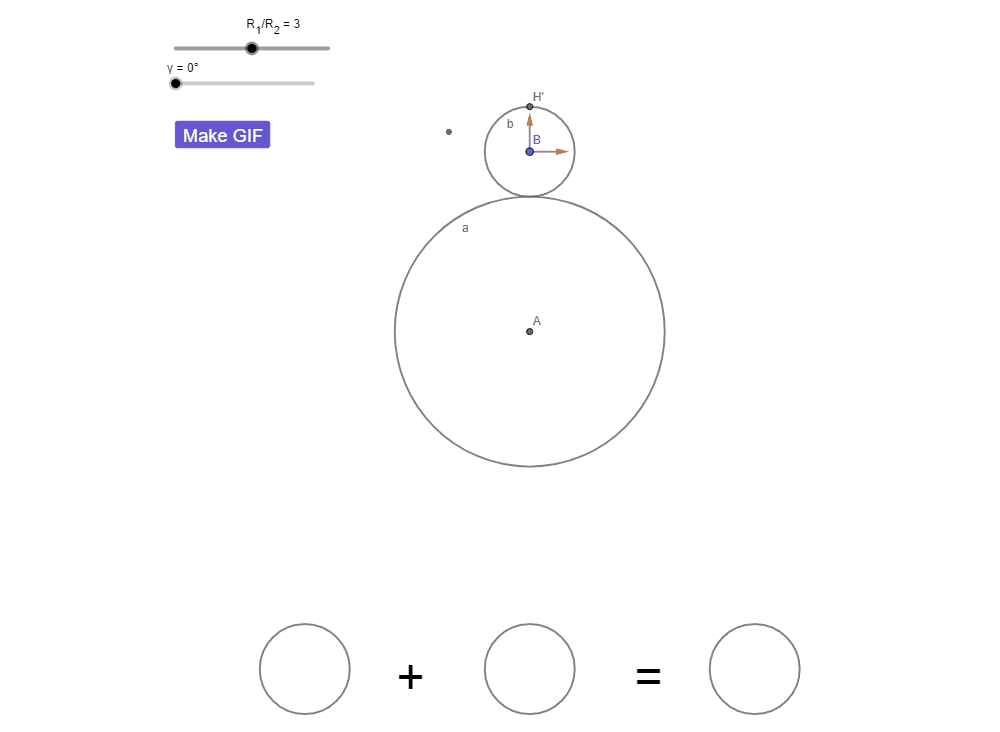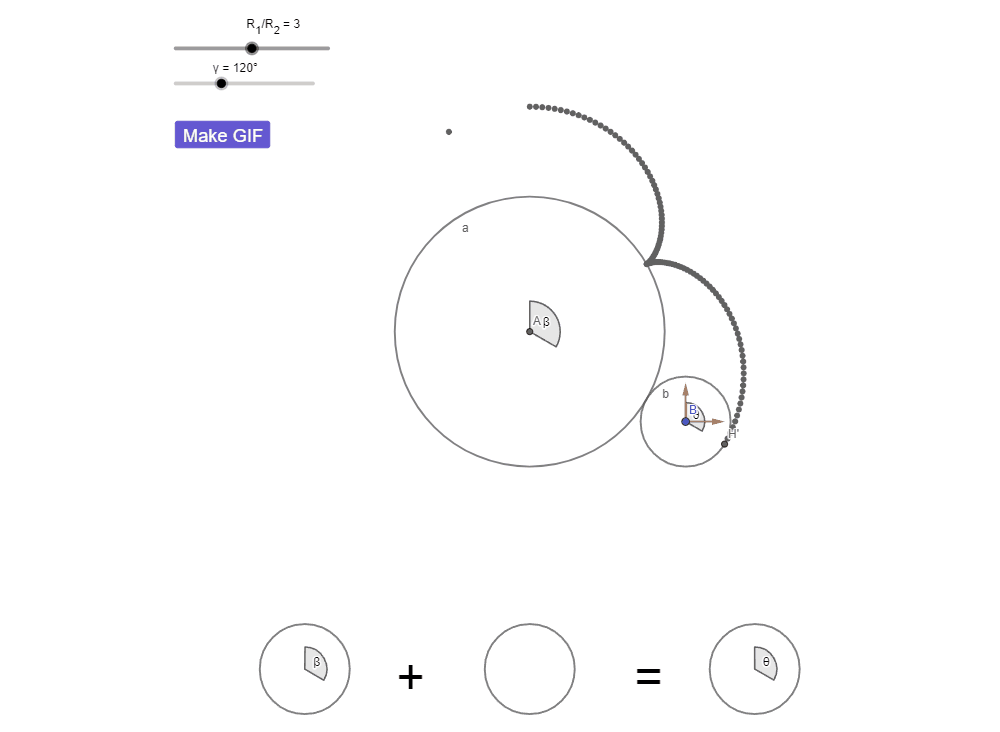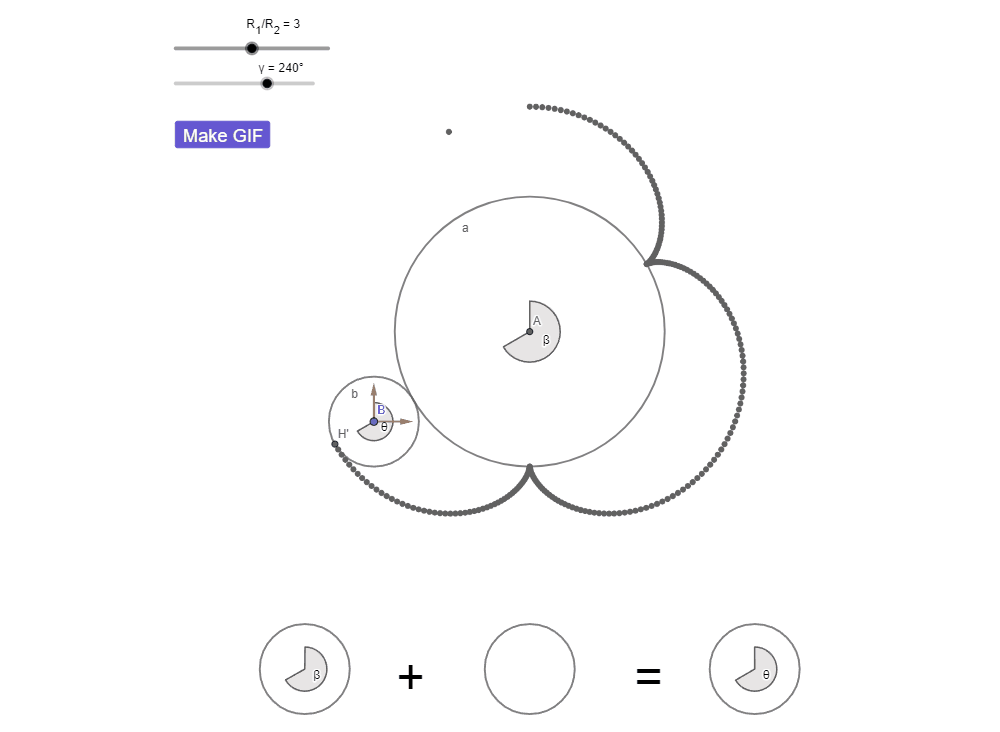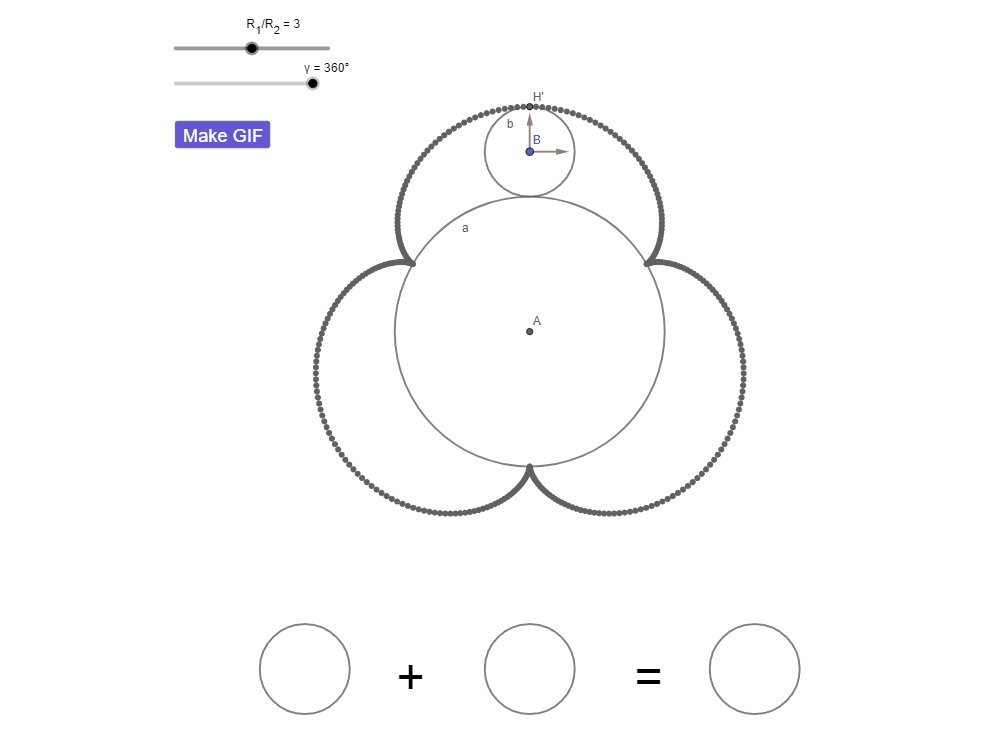
Думаю теперь вам не составило труда увидеть все 4 оборота.
Давайте проделаем тот же трюк, но со знакомыми нам предметами материального мира.
Положим на стол две одинаковые монеты так, чтобы они касались друг друга. Держа одну монету неподвижно, начнем вращать вокруг нее другую, избегая проскальзывания в точке соприкосновения монет - нам помогут насечки на ребрах. Заметим что к моменту когда монета достигнет противоположной стороны неподвижной монеты, она совершит один полный оборот. Продолжая вращать монету вернем ее в первоначальную позицию и отметим, что монета совершила еще один полный оборот. Парадоксальным образом монета прошла расстояние вдвое превышающее длину окружности второй монеты!

Проиллюстрируем вращение монеты с помощью геометрических построений.

Так в чем же секрет?!
Как и для любого хорошего фокуса, секрет в том, чтобы отвлечь внимание зрителя. Есть такой незамысловатый трюк, когда фокусник подбрасывает монету, делает вид что ловит ее правой рукой, но рука проходит немного выше и он ловит воздух, а монета падает в его левую руку. И пока зрители продолжают следить за правой рукой, думая что в ней монета, фокусник опускает монету в карман, затем раскрывает ладонь и показывает всем что монета исчезла.
Давайте возьмем две окружности с одинаковыми радиусами и пускай вместо того чтобы катиться, окружность b скользит по окружности a. Следите за точкой H.

Как видите, окружность совершает оборот, хоть и не вращается вокруг своего центра B.
Вернемся к задаче из теста и проделаем то же самое. Пускай окружность b просто скользит!

Надеюсь что теперь вы увидели "пропавший" оборот. Достаточно было внимательно наблюдать за тем, от чего вас отвлекли, чтобы разгадать секрет. Ведь этот дополнительный оборот - это оборот самой окружности b вокруг точки A!
Если вас заинтересовала статья и вы хотите узнать больше, советую посмотреть видео на канале Veritasium под названием The SAT Question Everyone Got Wrong. В нем намного подробнее рассказывается тема этой статьи.
Также можете взглянуть на статью в википедии Coin rotation paradox