Comments 332
Сколько токенов на это всё потратили?
Ну тут скорее дело не в токенах, а в книгах по истории математики.
Там, правда, больше перекос в историю, чем в математику, у меня наоборот.
Лучше уж перекос в историю, чем в нейрослоп.
Так тут нет нейрослопа совсем. Нейронка только картинки рисует.
Здесь реализован новый подход к объяснению темы комплексных чисел.
Мне кажется, тут слишком много текста для объяснения простой идеи, что i само по себе это не число, а умножение на i это операция поворота на 90 градусов.
Одно другого не отменяет. А всё потому, что . И, да, конечно, умножение комплексных чисел эквивалентно повороту на соответствующий угол.
Ну просто если цель объяснить комплексные числа, то для понимания этого достаточно. Нам этого не говорили ни в школе, ни в университете, а так было бы гораздо понятнее для многих.
i = (0, 1) это некорректная запись, она показывает только точку на плоскости и не показывает связь с поворотом. Точка (0, 1) это уже результат поворота, иначе мы рассматриваем просто двумерную плоскость с независимыми осями.
Не было бы понятнее. "Число это поворот" - с такой формулировкой согласиться либо тот кто уже относительно в теме либо просто примет на веру без понимания. Ну с таким же успехом он примет любое другое объяснение.
Какой поворот, где поворот, мы вроде тут вчера яблоки складывали, потом вычитали и получали долги а тут какие-то повороты и числа которые нельзя сравнивать между собой. Что вообще происходит?
Тут два выхода либо "заткнись и считай" либо переехать катком алгебры абсолютно все наивные представления о числах.
Число это не поворот. Число это число, поворот это поворот. Поворот это операция, такая же как сложение и умножение. i само по себе это не число, а операция. Соответствующую точку на плоскости можно обозначать (0, 1) или 1i. Сложение, умножение и применение i соответствуют аффинным преобразованиям плоскости сдвиг, масштабирование и поворот.
Очевидно что не такая же. Ни одна из этих операций(+,*) не позволяет выйти за рамки алгебраической структуры.
А вот "поворот" внезапно превращает число 3 в вектор 3i. Более того возникают вопросы - это мы "поворачиваем" число 3 или это мы масштабируем вектор i?
А мы и не выходим за рамки. Умножение в поле действительных чисел корректно определено и не выводит за их рамки. А умножение на i есть умножение в поле комплексных чисел, и тоже не выводит за их рамки. Ничего необычного.
Именно так, умножение есть умножение.
Но обратите внимание на всю ветку выше. Там утверждается что i это не число и вводится операция поворта числа.
Многие части обсуждения, как мне кажется, страдают от отсутствия точных определений, отсюда и возникает «чудо» и «магия» (более типичные для философии, нежели для точных наук).
Нету понятия «число», есть «действительное число» и «комплексное число». В рамках действительных чисел, i просто нет, т. к. квадрат действительного числа не может быть отрицательным. В рамках комплексных чисел i — это обычное число.
«Поворот чисел» возникает в рамках геометрической интерпретации комплексных чисел, ну окей, прикольный факт, полезен для привлечения геометрической интуиции.
Так надо рассматривать не алгебраическую структуру, а геометрическую плоскость. 2 измерения это плоскость. Рассматривать только алгебру можно, но тогда это и будет "заткнись и считай, просто правила такие", не будет понятно, почему они такие.
"поворот" внезапно превращает число 3 в вектор 3i
Если вы рассматривали поворот точки относительно начала координат, то и после поворота будет точка. Если вектор из нуля, то и после поворота будет вектор из нуля.
Более того возникают вопросы - это мы масштабируем вектор i?
Вот как раз если считать, что i это операция, а не число, то таких вопросов не возникает. Нельзя сказать "мы масштабируем вектор умножения", так и тут. i применяется к обычным действительным числам.
Так надо рассматривать не алгебраическую структуру, а геометрическую плоскость. 2 измерения это плоскость.
Так если вы оперируете 2 измерениями то у вас уже вектора а не числа, в смысле как точки на числовой прямой. Ну или хотя бы называйте их тогда комплексными числами. На них определены свои операции умножения и сложения и i выступает абсолютно рядовым участником а не операцией.
Вот как раз если считать, что i это операция, а не число, то таких вопросов не возникает. Нельзя сказать "мы масштабируем вектор умножения", так и тут. i применяется к обычным действительным числам.
Как вы будете возводить операцию в квадрат? Что такое e в степени операции? И еще миллион вопросов.
если вы оперируете 2 измерениями то у вас уже вектора а не числа
Нет, если вы рассматривали точки на числовой прямой, то в двух измерениях вы будете рассматривать точки на числовой плоскости. Точки сами по себе не превращаются в вектора, вектор это направленный отрезок из одной точки в другую. На одномерной числовой прямой вектора тоже есть.
Вообще лучше рассматривать комплексную плоскость как полярные координаты, а не как декартовы. Тут нет отдельной "мнимой" оси и отрицательных чисел. Отрицательные числа это лишь частный случай поворота на произвольный угол i^x, где x = 2, и направление тут идет от нуля в сторону -∞.
и i выступает абсолютно рядовым участником а не операцией
Вот именно об этом я и говорю. Если так считать, то будет непонятно, почему i^2 = -1. i это не число, рядовым участником можно считать точку 1i.
Как вы будете возводить операцию в квадрат?
Вот именно что никак. В квадрат возводится исходная единица, которую вы решили упростить. И даже так говорить некорректно, она не возводится в квадрат (вернее, не только возводится), а поворачивается. i^2 это 1ii. Даже умножение тут ставить неправильно. Это и есть то, что вызывает непонимание у многих, что и показывает этот диалог. i это не число, и умножать на него нельзя, так же как нельзя умножать на сложение. Причем это бинарная операция, i^1/3 это поворот на 30 градусов.
Замените i на вот такой знак "⟲", тогда будет понятнее.
1i^2 = 1ii = 1⟲2 = -1
Что такое e в степени операции?
Ничего, это бессмысленное высказывание. Поэтому я и говорю, что надо учитывать, что перед i есть коэффициент 1.
e^i = e^1i = e^(1⟲1). Берем число 1 (точку на комплексной плоскости), поворачиваем на 90 градусов относительно 0, получаем другое число, берем число e, с ними проводим операцию "возведение в степень". Не упрощайте единицу, тогда будет понятнее.
Кстати, у экспоненты операции в «большой» математике есть смысл: это сумма ряда (
— тождественная операция).
Замените i на вот такой знак "⟲", тогда будет понятнее.1i^2 = 1ii = 1⟲2 = -1
Вообще стало непонятно. Было возведение в квадрат стало почему то двойным поворотом. Было кубом стало тройным. А было 1/3 то стало поворотом на 30 градусов. Что-то сложение и умножение так с возведением в степень не композируются ни разу. А знаете что так композируется? Другое возведение в степень, она же экспонента. А мы тут усиленно делаем вид что это не она.
Ну серьезно, ведь вы же уже "посчитали" 1⟲1 перед тем как возводить в степень. Почему после возведения в степень оно(результат поворота) продолжает поворачиваться? Может потому что это все же не оператор а само свойство числа?
Вообще суть спора ускользает уже очень далеко. Вот есть число единица. Вы говорите что применяя к ней операцию поворота вы получаете некое, совсем другое число. При этом само число вы никак не называете, не определяете, вообще ничего с ним не делаете, разве что усердно избегаете называть это числом i. По сути вы тут даже никак не решили проблему понимания почему i^2 = -1. Просто зажмурились и решили что если число не называть то проблемы как бы и нет.
Ну логично что нет, ведь теперь перед тем как придти к i^2 = -1 нужно сначала понять чему равно 1⟲1, который другие люди и обозначали как i. А вы выкинули i как число и теперь сам вопрос почему i^2 = -1 бессмыслен. Ну потому что оператор такой, что непонятного то?
А если открыть глаза то внезапно оказывается что 1⟲1 совпадает с числом которое другие называют как i, чем вы и пользуетесь при вычислении экспоненты.
Можно точно так же интерпретировать -1. Мы не умножаем на -1, а делаем операцию поворота на 180 на числовой оси. И никакой -1 не существует.
А знаете что так композируется? Другое возведение в степень
Естественно. Можно сказать "сложение углов можно выразить через степень", а можно "степень можно выразить через сложение углов".
А мы тут усиленно делаем вид что это не она.
Мы пытаемся понять, почему ваша обычная положительная вторая степень дает отрицательное число. Что собственно и было причиной появления комплексных чисел. По вашим определениям степени квадрат не может давать отрицательное число.
Вообще суть спора ускользает уже очень далеко
Это вас надо спросить. Я не знаю, с чем и почему вы начали спорить, я просто отвечаю на ваши высказывания. Вы там приписали мне формулировку "Число это поворот" и начали с ней спорить.
Вот есть число единица. Вы говорите что применяя к ней операцию поворота вы получаете совсем другое число.
При этом само число вы никак не называете
Нет. Вы не поняли о чем речь. Я говорю, что применяя к единице операцию поворота 2 раза получается "-1". Получившееся число я называю - это "-1" (минус один).
разве что усердно избегаете называть это числом i
А для точки (0, 2) вы еще одну специальную букву будете использовать? А для точки (0, -1)? Почему вы усердно избегаете называть их буквами?)
Просто зажмурились и решили что если число не называть
Нет. Это не является моим аргументом ни в каком смысле, я про это ничего не говорил.
И никакой -1 не существует.
Я не говорил, что -1 не существует. Я не говорил, что i не существует.
Я сказал, что умножение на i в степени это операция поворота, на угол, соответствующий степени. Поэтому неправильно считать его обычным числом, у других обычных чисел таких свойств нет.
Можно точно так же интерпретировать -1. Мы не умножаем на -1, а делаем операцию поворота на 180 на числовой оси.
Всё верно, унарный минус это частный случай i^n, где n = 2.
Теперь подумайте, как интерпретировать умножение на "(-1)^(4/3)".
А если открыть глаза то внезапно оказывается что 1⟲1 совпадает с числом которое другие называют как i
В 20 раз объясняю, я в курсе, что эту точку общепринято называют i. Зачем вы мне это доказываете?
А 1⟲(1/3) почему-то не совпадает. Дальше что, еще одну букву будете вводить? Как вы вашими возведениями в квадрат объясните, почему это точка (√3/2, 1/2)?
Я объясняю, что это создает непонимание, так же как если "-1" обозначать знаком "-", и писать "-^2" вместо "(-1)^2".
Вообще стало непонятно.
Да, есть люди, которым непонятно даже объяснение "Поворачиваем отсюда сюда 2 раза, вот так и получается -1". Тут ничего не поделаешь.
По сути вы тут даже никак не решили проблему понимания почему i^2 = -1.
Решил, смотрите рисунок выше.
Да, есть люди, которым непонятно даже объяснение "Поворачиваем отсюда сюда 2 раза, вот так и получается -1". Тут ничего не поделаешь.
Нет. Вы не поняли о чем речь. Я говорю, что применяя к единице операцию поворота 2 раза получается "-1". Получившееся число я называю - это "-1" (минус один).
Хорошо я вижу дело не двигается, давайте по порядку, где тут ошибка?
1) у нас есть число 1.
2) Мы к нему применяем ваш поворот, и получаем число которое назовем Z. Специально не будем называть его i. Это число обладает очень интересными свойствами, например мы не можем сказать больше оно нуля или меньше но мы этому удивляться пока не будем. Главное что мы сейчас согласимся что это уже число, никакая ни операция, ни оператор, ни что либо еще.
3) Теперь мы не делаем никаких больше поворотов. Мы умножаем это число само на себя, обычная рутинная операция. Получаем -1. Заметьте, мы возведением в квадрат без каких-либо поворотов получили отрицательное число. Как это можно объяснить?
А если умножаем 3 раза(Z^4) то получаем изначальную единицу. То есть без всяких поворотов, на одном умножении мы получаем "анти-поворот".
4) Делаем из этого вывод что операции поворот либо не существует либо это то же самое что и умножение. В принципе эквивалентные понятия.
Мы к нему применяем ваш поворот
Это число обладает очень интересными свойствами
В концепции с моим поворотом оно не обладает никакими интересными свойствами. Это просто число, точка на плоскости, ничем не отличающаяся от других. Интересными свойствами обладает поворот.
Вот здесь и ошибка.
Мы умножаем это число само на себя, обычная рутинная операция. Получаем -1.
С чего мы вдруг получили -1? Без поворота вы останетесь на той же оси.
"Обычная рутинная операция" умножения для положительных чисел на действительной оси дает числа на той же оси с тем же знаком. "1*1 = 1"
Поэтому для положительной единицы на другой оси "обычное умножение" должно давать "i*i = i".
Иначе вам надо вводить необычное умножение, которое меняет ось, и именно на 90 градусов против часовой стрелки.
Вот здесь и ошибка.
Заметьте, мы возведением в квадрат без каких-либо поворотов
Ага, без поворотов переместились на другую ось. Магия, не иначе.
Вот здесь и ошибка.
Делаем из этого вывод что операции поворот либо не существует либо это то же самое что и умножение
Это неправильный вывод. Умножая 1 на 1 вы не получите никакой минус. Поэтому это не то же самое, что умножение.
Без поворотов вы не узнаете, где находится точка i^(1/2) и почему возведение ее в квадрат дает i, а не -i. Вы же выше ввели операцию, при которой возведение в квадрат внезапно без причин дает минус.
С чего мы вдруг получили -1?
По правилам умножения комплексных чисел.
"Обычная рутинная операция" умножения для положительных чисел на действительной оси дает числа на той же оси с тем же знаком. "1*1 = 1"Поэтому для положительной единицы на другой оси "обычное умножение" должно давать "i*i = i".Иначе вам надо вводить необычное умножение, которое меняет ось, и именно на 90 градусов против часовой стрелки.Вот здесь и ошибка.
1) 1⟲1 = Z, по вашему же определению.
2) Z * Z = -1 по правилам умножения комплексных чисел.
Вы утверждаете что правила не верны или что у вас другое какое-то умножение с другими свойствами? Или у вас Z не комплексное число? В чем тут именно ошибка?
Умножая 1 на 1 вы не получите никакой минус. Поэтому это не то же самое, что умножение.
Так я 1 на 1 и не умножаю, зачем вы мне это приписываете? Умножается Z на Z.
По правилам умножения комплексных чисел.
Каким таким правилам, у нас их еще нет, мы их только вводим. Вы сказали "давайте по порядку", а сами перескакиваете. Я предлагаю вводить умножение комплексных чисел через концепцию поворота.
Как это можно объяснить?
Возвращаю вам ваш вопрос. Как можно объяснить ваше правило умножения комплексных чисел, что "i*i = -1"? А никак, вы его постулируете.
Как можно объяснить, что "i^(1/3) = √3/2 + 1/2i"? А никак, в вашем умножении степеней даже постулата такого нет, вам надо еще один постулат вводить.
А в моем подходе это объясняется поворотом. Он просто объясняет ваши аксиомы.
Вы утверждаете что правила не верны или что у вас другое какое-то умножение с другими свойствами?
Я утверждаю, что у вас без поворота будет обычно умножение, аналогичное умножению вещественных чисел.
В чем тут именно ошибка?
Я написал, в чем именно ошибка, 3 раза в предыдущем комментарии. Если вам непонятно объяснение, задавайте более конкретный вопрос по тому, что там написано, а не по новому тексту, который вы написали сами.
Так я 1 на 1 и не умножаю, зачем вы мне это приписываете?
Умножается Z на Z.
Затем, что вы сказали "умножаем, обычная рутинная операция". "Обычная", значит такая же, какая была для 1*1.
i применяется к обычным действительным числам.
Т.е., надо писать не 3i, а i(3)? Что возварщает эта функция? А так i(i) тоже можно?
Там смысл в том, что переосмысляем сначала обычные числа геометрически. Умножение на положительное число тогда дает растяжение-сжатие, на минус единицу центральное отражение. Тогда мнимая единица дает поворот.
Тут как геометрическая алгебра в , только не на векторной плоскости, а на числовой. Если же рассматривать двумерную геометрическую алгебру, то комплексная числовая плоскость изображает четную подалгебру в Cl(2,0,0).
Ваналогичная четная подалгебра — дает кватернионы.
Прикол еще в том, Cl(2,0,0) изоморфна алгебре всех вещественных матриц 2 на 2, а Cl(3,0,0) — всех комплексных матриц 2 на 2. Я вообще за то, чтобы популяризировать теорию всех комплексных матриц 2 на 2, как минимум. Там очень много геометрического смысла, и эффективных методов вычислений (например, от любых таких матриц легко считать любые аналитические функции, если знать как, а вот в более сложных случаях уже нет, грубо можно сказать комплексные матрицы 2 на 2 являются объектом максимальной сложности, на котором аналитические функции определены максимально просто — для всех объектов проще есть простые явные формулы для них, а для всех объектов сложнее их уже нет).
А для умножения вы пишете *(3)? Это бинарная операция, что и на сколько поворачиваем. Можно писать 3i = 3i^1 = 3i1, если использовать i аналогично другим знакам операций - 3+1, 3*1. Или можно сделать специальный знак 3i = 3⟲1.
Это бинарная операция,
Возвращаемся к вашему предыдущему сообщению, где вы написали:
i применяется к обычным действительным числам.
Это утверждение интерпретируется единственным способом, как унарная операция или функция с одним аргументом, являющимся вещественным числом. Ладно, не важно, пусть бинарная, первый аргумент - вещественное число. А тип второго? И тип результата? Явно не вещественное число. Что тогда?
Если у i задана степень 1, то унарная. А в общем случае это ai^b. Я говорю степень, потому что это общепринятое название, чтобы было понятно, а так это величина поворота.
a+b - сдвигаем a на величину b.
a⟲b = ai^b - поворачиваем a на величину b.
Типы всех величин это вещественные числа. В том и смысл, с операцией поворота любую точку на плоскости можно задать с помощью вещественных положительных чисел.
Типы всех величин это вещественные числа.
Это у аргументов, а у результата?
Ну да, результат это комплексное число. Поворот добавляет второй компонент.
комплексное число.
А что это такое с вашей точки зрения? Какой математический объект?
Поворот добавляет второй компонент.
И еще одно, какой нафиг поворот для "пространства", где сами оси крутить нельзя, ибо у объектов на оси X их квадрат положителен, а для объектов на оси Y - отрицателен.
i - элемент множества комплексных чисел. То есть вполне себе число. А вот умножение на число i - уже можно интерпретировать как поворот. Как и умножение на любое другое число, вещественное или комплексное.
Нет, элемент множества комплексных чисел можно записать как 1i. А само по себе i правильнее считать операцией. Так сразу понятно, почему применение i два раза дает -1 - потому что мы применяем поворот к обычной единице.
В этом как раз и возникает путаница. Потому что обычно считается, что i это число, и мы на него умножаем.
То, что вы рассказываете — это геометрическая интерпретация комплексных чисел. А нормальное определение этих самых комплексных чисел — простое расширение поля действительных чисел элементом i с правилом i × i = −1. При этом i получается таким же числом, как и все остальные.
Так у нас разговор о том, как понять, откуда появляется это правило. У остальных чисел таких правил нет.
На самом деле, вместо присоединения i, можно строить комплексные числа при помощи присоединения j = . Это будет поворот на 60 градусов. (Вообще, достаточно присоединить любое комплексное недействительное число.)
Есть, только для такой детализации редко нужда возникает и, в итоге, про нее нематематикам редко рассказывают. Нужда, конечно, ненулевая. Пример. Пусть есть библиотека для "точной" арифметики рациональных чисел. Держим целочисленную пару (числитель, знаменатель). А потом, раз, и нужен квадратный корень из двух. Достаточно вместо одной пары держать две. В этой системе рациональных чисел, расширенной квадратным корнем из двух, полезут все те же геометрические интерпретации и повороты.
Так у нас разговор о том, как понять, откуда появляется это правило
Случайным образом. Именно этот вариант оказался полезным на практике, в теории колебаний, электротехнике, етс. Остальные - умерли за ненадобностью.
Вот дело как раз в том, что можно именно объяснить и показать, как появляется -1, а не просто считать это аксиомой, которую кто-то придумал.
можно именно объяснить и показать
Ну, давайте, используя ваши объяснения, покажите, почему комплексные числа удобны в теории колебаний, электротехнике и пр.
- можно объяснить и показать, как появляется -1
- давайте, покажите, почему комплексные числа удобны в теории колебаний
Не вижу связи. Я сказал, что можно показать, как появляется -1, а не почему они удобны в теории колебаний.
можно показать, как появляется -1
-1, это вообще-то обычное целое число... Но тут еще спрятался более интересный вопрос: и где же конкретно это комплексное число, обычно обозначаемое буквой "i", появляется?
Объясняю еще раз. Я отвечал на комментарий "новый подход к объяснению темы комплексных чисел". В объяснении темы комплексных чисел, для людей которые с ней не знакомы, основная сложность это понять, почему i*i дает -1. Не наоборот, потому что корни из -1 при изучении этой темы никто не считает, большинство примеров связаны с умножением выражений "a+ib". Вы предлагаете подход "заткнись и считай, я так сказал". Я предлагаю простое и наглядное объяснение. Для неспециалистов.
Вы предлагаете ввести аксиому "i*i = -1". Ваш подход не объясняет, как считать "(-i)*(-i)" - нужна ли тут другая аксиома "(-i)*(-i) = +i", чтобы расчеты были аналогичны "(-1)*(-1) = +1", или считать в рамках той же "(-i)*(-i) = -1". Также ваш подход не объясняет, как посчитать "i^(1/3)". Видимо вам нужна какая-то третья аксиома. Концепция поворота против часовой стрелки относительно начала координат это наглядно объясняет - поворачиваем исходную точку на прямой действительных чисел на 90*2 или 90*1/3 градусов.
и где же конкретно это комплексное число, обычно обозначаемое буквой "i"
Я с самого начала объясняю, что такое обозначение создает путаницу и непонимание. Да, несмотря на то, что оно общепринятое. Да, несмотря на то, что вы лично для себя считаете его понятным.
Нет, элемент множества комплексных чисел можно записать как 1i
Может и можно, но обычно записывается просто как i.
А само по себе i правильнее считать операцией.
Что значит "правильнее"? Есть определение множества комплексных чисел (несколько эквивалентных определений). Это просто множество каких-то элементов. А не операций. А уже операции на этом множестве можно геометрически интерпретировать как повороты. Именно операции, а не элементы.
но обычно записывается просто как i
Я про это и говорю. Это и вызывает непонимание. Эта ветка началась с комментария "новый подход к объяснению темы комплексных чисел".
Что значит "правильнее"?
Ну то и значит. Более соответствует назначению, геометрическому смыслу, проще для понимания, требует меньше аксиом "ну вот так мы договорились".
Именно операции, а не элементы.
Я так и сказал. i сама по себе это операция, а не элемент. Элемент это 1i^1 или (0, 1). "i в степени 1" это аналог унарного минуса. Вы же не считаете унарный минус в "-1" элементом.
элемент множества комплексных чисел можно записать как 1i
Элемент это 1i^1
Налицо эволюция записи элементов. Давайте пойдем еще дальше, и запишем элемент как 1*1*(2-1)*1*(3-2)*i^1^1^1^1. Явно еще проще будет:)
Совершенно непонятно, что такого сложного в абсолютно ясной и прозрачной идее добавления нового элемента к существующему множеству (вещественных чисел). Более того, в математике эта тема всплывает раз за разом, буквально на каждом шагу. Если даже на этом этапе возникают трудности, для которых нужно придумывать такие костыли - то пожалуй такому человеку заниматься математикой и не стоит вовсе.
Основная сложность в изучении комплексных чисел - понять, почему "i*i = -1". Всё остальное это стандартные правила выражений.
Явно еще проще будет
Вы предлагаете то же самое, что упростить выражение "-1" до "-". То есть "6 - 7 = -". Проще? Да. Понятнее? Нет. Правильнее? Тоже нет.
почему "i*i = -1
По определению мнимой единицы, больше ни по чему. Символом i обозначается корень уравнения x^2 + 1 = 0.
Вы предлагаете
Я ничего не предлагаю. Я просто говорю, как определяется понятие "множество комплексных чисел". Определения не могут быть "правильными" или "неправильными".
Разумеется может. Первородное число - это такое чётное натуральное число, которое заканчивается на 1.
И что в этом определении "неправильного"?
Даже не знаю.. возможно то, что оно противоречит само себе?
Каким образом противоречит?
Определение: Первородное число - это такое чётное натуральное число, которое заканчивается на 1.
Теорема: Множество первородных чисел - пустое.
Доказательство: Тривиальное.
В чем проблема? В любом случае, все это совершенно не касается предыдущего разговора про определение мнимой единицы.
По определению мнимой единицы, больше ни по чему.
Вот я и объясняю, что можно объяснить это более понятно для изучающих эту тему, чем "заткнись и считай, я так сказал". У вас это аксиома, у меня нет. Я предложил подход, где это является логичным следствием.
Давайте пойдем еще дальше
Я ничего не предлагаю.
Именно предлагаете, "давайте пойдем" это предложение. И судя по контексту, предлагаете вы противоположное написанному.
Определения не могут быть "правильными" или "неправильными".
Тогда непонятно, с чем вы спорите. Я предложил свои определения, которые считаю более понятными для изучающих тему, они дают картину, эквивалентную исходной.
"заткнись и считай, я так сказал"
Да, вместо этого: "заткнись и поворачивай, я так сказал":)
Тогда непонятно, с чем вы спорите. Я предложил свои определения, которые считаю более понятными для изучающих тему, они дают картину, эквивалентную исходной.
С геометрической интерпретацией операции умножения комплексных чисел никто не спорит. Но вы заявили, что
i само по себе это не число
что напрямую противоречит общепринятому определению понятия "множество комплексных чисел".
Да, вместо этого: "заткнись и поворачивай, я так сказал"
Да, только во-первых, концепция поворота и используется не только в математике и понятна всем, во-вторых, она объясняет сразу многие вещи - откуда берется -1, где находится i^(1/3), и почему (-i)*(-i) тоже равно -1. А с вашим подходом даже Эйлер с Безу определиться не могли.
Но вы заявили, что i само по себе это не число
что напрямую противоречит общепринятому определению
Я знаю, что это противоречит общепринятому определению. Это и есть причина, почему я так заявил. Я считаю, что такое определение вносит путаницу. Можно сколько угодно определять, что "-" это число, и писать "- * - = 1", только понятнее будет обозначать эту точку "-1".
Я считаю, что такое определение вносит путаницу.
А, ну ваше право, считайте. Только люди когда интересуются комплексными числами, наверное все же хотят узнать именно про комплексные числа в общепринятом смысле. А не про "комплексные числа в определении michael_v89". Ну это так, вам для размышлений:)
Большинство людей не "интересуется комплексными числами", а изучает их в школе потому что учитель так сказал. У них обычно вызывает непонимание, почему i*i равно -1, что в общепринятом смысле задается аксиомой без объяснения. Мой первый комментарий в этой ветке содержит фразу "для объяснения простой идеи, что умножение на i это операция поворота на 90 градусов". Это так, вам для размышлений. О том, с чем конкретно вы спорили.
Мое определение комплексных чисел, как ни странно, не отличается от общепринятого. В общепринятой математике математике выражения "i" и "1i" эквивалентны. Отличается только то, что я называю i, при этом даже это необязательно, как я показал выше со знаком ⟲. Я только объясняю то, что в общепринятом смысле задается аксиомой.
Я знаю, что это противоречит общепринятому определению. Это и есть причина, почему я так заявил.
Мое определение комплексных чисел, как ни странно, не отличается от общепринятого.
Определитесь уже.
почему i*i равно -1, что в общепринятом смысле задается аксиомой без объяснения
Ну поворот на 90 градусов - это такая же аксиома без объяснений. Почему и зачем вообще поворот? Почему на 90, а не на 89 или 125?
Определитесь уже.
Не вырывайте фразы из контекста. Я отвечал на комментарий
"вы заявили, что i само по себе это не число, что напрямую противоречит общепринятому определению".
Вы говорили про определение i, а не про определение комплексных чисел, которое определяется через i.
В предыдущем комментарии я так и написал "Отличается только то, что я называю i".
Ну поворот на 90 градусов - это такая же аксиома без объяснений.
И? Напоминаю, что разговор был про объяснение темы. А основную сложность в ней вызывает вопрос, как получается -1. Если мы это наглядно объяснили, значит достигли цели.
Тем не менее, это факт даже без явного введения такого правила, умножение на i поворачивает исходную точку на 90 градусов относительно нуля. Можете проверить в любом математическом пакете с любым комплексным числом. А вот потом попробуйте ответить на вопрос, почему математические пакеты поворачивают не на 89.
Отличается только то, что я называю i
Ну вот, а изучать обычно полезно то, что весь остальной мир называет i. А не один какой-то рандомный интернет пользователь.
почему математические пакеты поворачивают не на 89
Потому что, по определению, i*i = -1. То есть, это первичное определение. А уже повороты из него следуют.
Я разве где-то сказал, что не надо изучать то, что весь остальной мир называет i?
Я вообще вам советую подумать, почему люди пишут разные учебники на одну тему, разные статьи на известные темы, и вообще строят разные теории и разные подходы.
То есть, это первичное определение.
Я так и сказал, у вас это аксиома, у меня следствие поворота. Зачем вы мне то же самое повторяете? У вас нельзя понять, почему так, надо только запомнить. В моем подходе понять можно. Для того он и нужен.
А уже повороты из него следуют.
Нет, поворот для i^(1/3) для него не следует. Из него даже не следует, что i*i это поворот чего-то куда-то. У вас это аксиома без всякой связи с поворотами.
Ваш собеседник предлагает вводить через алгебраическую аксиому (как расширение поля), а вы предлагаете сразу вводить поворот. Проблема первого способа в том, что так ничего непонятно, проблема второго в том, что поворот как будто ниоткуда взялся. Я сам третий подход собираюсь показать: комплексные числа появляются в геометрической алгебре.
почему люди пишут разные учебники на одну тему, разные статьи на известные темы, и вообще строят разные теории и разные подходы.
Комплексных чисел это не касается. Их весь мир (кроме вас) понимает одинаково.
В моем подходе понять можно.
В вашем подходе нельзя понять, откуда взялся поворот на 90 градусов. Кроме того, что важнее, ваше разделение элементов множества комплексных чисел на "числа" и "операторы" приводит к ненужной путанице и несамосогласованности. В общем, хороший тупиковый путь в никуда, обрезающий возможность дальнейшего знакомства с общепринятой математической теорией. Впрочем, если человек не может понять і*і=-1 безо всяких геометрических выкрутасов - то ему это дальнейшее знакомство наверное и не сильно нужно.
В вашем подходе нельзя понять, откуда взялся поворот на 90 градусов.
Повторяю вопрос, который вы проигнорировали. И? Какой вывод должен быть в контексте этой дискуссии?
А откуда взялось сложение и умножение?
У меня нет "поворота на 90 градусов", у меня есть "поворот на заданный угол", угол задается степенью i.
Комплексных чисел это не касается.
Ага, то есть вы утверждаете, что по комплексным числам есть только один учебник с одним объяснением, и никаких статей с альтернативными объяснениями нет? Вы не забыли, какую статью комментируете? Мое объяснение не отличается от этой статьи. Я предлагаю объяснение, которое с моей точки зрения будет понятнее для начинающих.
Кроме того, что важнее, ваше разделение элементов множества комплексных чисел на "числа" и "операторы"
У меня нет разделения элементов множества комплексных чисел на "числа" и "операторы". Операторы это не элементы множества комплексных чисел, так же как '+', '-', и '*' это не элементы множества натуральных чисел.
обрезающий возможность дальнейшего знакомства с общепринятой математической теорией
Повторяю вопрос, который вы проигнорировали. Я разве где-то сказал, что не надо знакомиться с общепринятой математической теорией?
В общепринятой теории возведение в комплексную степень вычислеяется через синус и косинус угла. Как же так, вы только что доказывали, что в ней никаких поворотов нет?
Впрочем, если человек не может понять і*і=-1
В такой форме это нельзя "понять", потому что тут нечего понимать, это можно только "запомнить".
Их весь мир (кроме вас) понимает одинаково.
Понятно, переходы на личности начались. Видимо других аргументов уже не осталось.
У меня нет "поворота на 90 градусов", у меня есть "поворот на заданный угол", угол задается степенью i.
Хорошо, откуда взялся поворот на "заданный угол", и почему этот угол задается именно степенью i, а не чем-то другим?
И? Какой вывод должен быть в контексте этой дискуссии?
Тем, что ваш подход точно такой же аксиоматический, как и любой другой. Только с тем еще дополнительным недостатком, что является некорректным и несамосогласованным.
Ага, то есть вы утверждаете, что по комплексным числам есть только один учебник с одним объяснением, и никаких статей с альтернативными объяснениями нет?
Нет никаких "альтернативных объяснений". Объяснения могут быть разными словами, но всегда про одни и те же комплексные числа.
Вы не забыли, какую статью комментируете?
Я нейрослоп этого автора не читаю, так что хз, что там у него наляпано в статье. В данном случае я комментирую не статью, а ваши математически безграмотные заявления.
Я разве где-то сказал, что не надо знакомиться с общепринятой математической теорией?
Так нужно сразу учиться правильно. А не сначала выучить черте-что по вашему "подходу", а потом переучиваться нормально.
Как же так, вы только что доказывали, что в ней никаких поворотов нет?
Еще раз: с геометрической ИНТЕРПРЕТАЦИЕЙ УМНОЖЕНИЯ НА КОМПЛЕКСНОЕ ЧИСЛО никто не спорит. Я просто указал вам на некорректность вот этой фразы:
i само по себе это не число
Которая не является "другим взглядом" или "альтернативным объяснением" или еще чем-то в другом роде. А является просто-напросто неверным (или безграмотным) утверждением. То, что вы уже столько времени не можете этого понять - лучшее доказательство того, что ваш "подход" ведет в тупик, и поэтому крайне вреден для обучающихся.
Хорошо, откуда взялся поворот на "заданный угол", и почему этот угол задается именно степенью i, а не чем-то другим?
Оттуда же, откуда взялось сложение и умножение. Ответьте для себя на вопрос, откуда они взялись, так чтобы вам самому было понятно, вот и ответ на ваш вопрос будет аналогичный.
Я просто указал вам на некорректность вот этой фразы:
i само по себе это не число
А я вам объяснил, что так и задумано. Эта фраза появилась именно как противопоставление общепринятому определению. Я не понимаю, зачем вы мне доказываете, что такое i по общепринятому определению. Я и так про это в курсе.
является некорректным и несамосогласованным.
Там нет никакого несогласования. Я только детализировал понятие i. Для этого надо или поменять определение i, превратив его из аксиомы в вывод, или ввести новые обозначения для деталей. Все остальные определения и расчеты остаются без изменений.
Тем, что ваш подход точно такой же аксиоматический, как и любой другой
Еще раз объясняю, разговор не о том, чтобы построить строгую математическую теорию без аксиом, а о том, как объяснить тему людям, которые ее изучают.
Даже если считать операцию поворота аксиомой, она одна заменяет множество аксиом вашего подхода, поэтому я считаю, что такое объяснение проще для понимания. Для меня оно точно проще, и возможно я не один такой.
Для меня оно точно проще, и возможно я не один такой.
Ну, дело ваше. Главное, что студентов вы учить не будете, поэтому шанс кому-то навредить у вас минимальный. А для себя иметь неверные математические представления - это не страшно. Куча людей с таким живут, не вы первый, не вы последний:)
Ага, а сможете сформулировать, что конкретно неверно в этих представлениях, кроме несоответствия определения i общепринятому, что и было целью? Я в этом сомневаюсь. С математической точки зрения мой подход эквивалентен общепринятому, все формулы верны в рамках обозначений, в расчетах получаются такие же результаты.
Ага, а сможете сформулировать, что конкретно неверно в этих представлениях,
Не то, чтобы неверно, но попробуйте написать библиотеку для работы с комплексными числами, явно основанную на вашем подходе. Аналог std::complex для C++. В питоне - комплексные числа встроены в язык. Ну только что можно cmath переписать.
Можете еше попробовать статью в серьезный математический журнал написать.
Если в ту фирму, где я работаю, на собеседование придет человек, исповедующий такой альтернативный подход, то никакие соображения инклюзивности его не спасут. Кольцо в носу могут и не заметить, а вот использование нестандартной базовой математики будет явной потенциальной проблемой.
Какое еще исповедование подхода на собеседовании? Разговор о том, как наглядно объяснить изучающим тему, почему i*i = -1. Сколько раз можно объяснять...
попробуйте написать библиотеку для работы с комплексными числами, явно основанную на вашем подходе. Аналог std::complex для C++.
Как ни странно, std::complex для C++ вполне соответствует моему подходу. В моем подходе (0,1) * (0,1) = (-1,0).
Но вообще я вижу там вызовы std::polar() в коде вычисления степени. Наверно есть какая-то связь с углами?
Ага, а сможете сформулировать, что конкретно неверно в этих представлениях
Вам уже сто раз об этом написали. Мнимая единица - это элемент множества комплексных чисел. По определению. Если вы заявляете иначе - это неверно.
Вот только в алгебраической записи комплексного числа -- это совсем не обязательно мнимая единица.
Обязательно.
Нет. Читайте "Избранные вопросы математики. 10 класс. Факультативный курс" под редакцией В. В. Фирсова.
Дайте ссылку на конкретную страницу и абзац.
Страница 64. Параграф 3 под названием "Комплексные числа". И до конца страницы. Ключевое место:
Знак
здесь также ничего не обозначает.
Также см. последний абзац на странице 88 о двух смыслах .
Ничего не нашел там про то, что i -
это совсем не обязательно мнимая единица
Более того, как раз на странице 88 и доказывается, что формальное выражение 0+1i и число i - это одно и то же. То есть, их можно не различать.
На всякий случай, вот ссылка на книжку (1980 год, однако): https://www.mathedu.ru/text/izbrannye_voprosy_matematiki_10_klass_fakult_kurs_1980/p89/
Ну а по делу, автор начинает с обозначения a+bi, а мы с эквивалентной пары (a, b). Поэтому автору приходится переобуваться на ходу, переобозначая i, а нам нет.
Вам уже сто раз об этом написали. Мнимая единица
Именно поэтому я написал "кроме несоответствия определения i". Если вы не хотите отвечать на заданный вопрос, просто не отвечайте.
Мнимая единица - это элемент множества комплексных чисел. Если вы заявляете иначе
Да не заявляю я иначе. Еще раз объясняю.
"Мнимая единица" по определению это "комплексное число, квадрат которого равен -1". Это точка (0, 1). У меня эта точка никуда не делась и является элементом множества комплексных чисел. В моем подходе "(0, 1) * (0, 1) = (-1, 0)", я повторил это уже много раз.
Просто вы по историческим причинам обозначаете эту точку i, а я говорю, что это то же самое, что по историческим причинам обозначать "-1" знаком "-". Можно так обозначать? Можно. Понятно это будет для начинающих? Не очень. Вы понимаете разницу между комплексным числом и его обозначением?
Можно заменить выражение "i*i" на "1*i*i", тогда "i" всегда будет использоваться только после умножения, и можно считать "*i" отдельной операцией. Тогда не будет необходимости вводить какие-то специальные элементы множества со специальными обозначениями и специальными правилами умножения, всё будет более универсально.
Вы понимаете разницу между комплексным числом и его обозначением?
Да. Все обозначения одного и того же числа эквивалентны между собой. 2 = 4/2 = 7-5 = 128/64 = ...
Точно так же, i = (0,1) = 0*1 + 1*i = 1*i^1 = ... и так далее. Все это разные обозначения одного и того же числа.
Можно заменить выражение "i*i" на "1*i*i"
Можно
можно считать "*i" отдельной операцией
Можно. Но вы же раньше заявляли, что операция - это именно "i", а не "*i". Со вторым нет никаких претензий, это стандартная геометрическая интерпретация умножения на комплексное число i.
Все это разные обозначения одного и того же числа.
Правильно. А я в рамках своего подхода поменял обозначения, и i у меня обозначает операцию, а не число. О чем я прямо написал. Поэтому ваше утверждение "Вы заявляете, что мнимая единица это не элемент множества комплексных чисел" неверно.
Мнимая единица как была так и осталась, просто я не обозначаю ее i.
- можно считать "*i" отдельной операцией
- вы же раньше заявляли, что операция - это именно "i
В моем первом комментарии есть фраза "умножение на i это операция поворота на 90 градусов".
Далее я писал "i само по себе это не число, а операция", в рамках моего объяснения это корректное выражение. Если у нас i участвует только в операции умножения, то нет смысла рассматривать его отдельно.
И я это писал в контексте объяснения для начинающих, у меня не было цели давать строго выверенные формулировки.
i само по себе это не число, а операция", в рамках моего объяснения это корректное выражение.
Это не может быть "корректным выражением", потому что это попросту ложное утверждение.
Все, мне надоело толочь воду в ступе. Слова богу, школьники и студенты с вашими "объяснениями" не столкнутся, поэтому шанс нанести им вред у вас минимальный. А для себя вы в праве считать любую чушь, никто вам не запретит. На том и закончим.
Нет, в рамках моих определений это не ложное утверждение. "Определения не могут быть "правильными" или "неправильными"".
"Определения не могут быть "правильными" или "неправильными""
Зато могут быть полезными или бесполезными. Ваше - бесполезное, потому что из него следует, что i (оператор) не равно 1*i (число). Что полная чушь, от которой все равно придется избавляться. В общем, чтобы претендовать на какую-то методику обучения, необходимо, во-первых, чтобы ваша "теория" была, как минимум, самосогласована, и все нужные определения и теоремы логично связаны. А во-вторых - учитывать дальнейшую траекторию обучающихся, чтобы не приходилось переучиваться заново.
Человек же, у которого возникают трудности уже с пониманием i*i=-1 - едва ли может выдумать какую-то полезную методику объяснения, что вы и продемонстрировали своим примером.
потому что из него следует, что i (оператор) не равно 1*i (число). Что полная чушь
А почему оператор должен быть равен числу?
Это такая же чушь, как утверждение "'-' (оператор) должен быть равен '-1' (число)".
Если "i" это оператор, то и писать надо "1i" или "i1", а не "1*i". Я вам уже объяснил, что в строгом смысле оператором надо считать "*i", и тогда умножение из выражений исчезает. Требуете строгих формулировок, а сами им не следуете.
В общем, чтобы претендовать на какую-то методику обучения
Да не претендую я ни на какую методику обучения, много раз уже сказал. Я предлагаю объяснение того же, чему учите людей вы, которое проще для понимания.
во-первых, чтобы ваша "теория" была, как минимум, самосогласована, и все нужные определения и теоремы логично связаны
Моя "теория" самосогласована, и все нужные определения и теоремы логично связаны. Я вам задал прямой вопрос привести примеры несогласованности, вы смогли привести только несоответствие определения i общепринятому, что и было целью.
Ну, как знаете. Успехов:)
Моя "теория" самосогласована, и все нужные определения и теоремы логично связаны. Я вам задал прямой вопрос привести примеры несогласованности,
Вот ваше утверждение https://habr.com/ru/articles/981234/comments/#comment_29329878 о том, что уравнение X^3=-1 имеет не 3 решения, а бесконечное количество:
А вот дело как раз в том, как узнать, что там есть третий корень, и почему их на самом деле не 3, а бесконечно много.
Вы привели цитату, а где тут несогласованность? Несогласованность чего с чем?
См. например, https://en.wikipedia.org/wiki/Fundamental_theorem_of_algebra, где утверждается, что:
The theorem is also stated as follows: every non-zero, single-variable, degree n polynomial with complex coefficients has, counted with multiplicity, exactly n complex roots.
Ваша "теория" дает ответ, отличающийся (несогласованный с) от ответа, получаемого в рамках стандартного аксиоматического подхода. Ваши "комплексные" числа - не наши. Вы "объясняете" что-то лишь похожее на "стандартные" комплексные числа.
Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).
Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.
Про корни говорят, что они удовлетворяют данному уравнению.
Решить уравнение означает найти множество всех его решений (корней).
(1/2 + i^9 *sqrt(3)/2)^3 = -1
(1/2 + i^17*sqrt(3)/2)^3 = -1
(1/2 + i^9 *sqrt(3)/2) в третьей степени дает -1? Дает. Поэтому "решений на самом деле не 3" это корректное высказывание.
Если вы скажете, что это одна и та же точка, подумайте, сколько корней у уравнения x^3 = 0. Здесь высказывание "решений на самом деле не одно" тоже корректное.
И да, вы опять начали рассказывать про несоответствие моих неформальных высказываний общепринятой теории, хотя разговор был про самосогласованость моей "теории".
(1/2 + i^9 *sqrt(3)/2)
Я не вижу в ваших формулах ту неизвестную величину, которую нужно найти. Это не полиномиальные уравнения в отличие от X^3+1=0
сколько корней у уравнения x^3 = 0
Почитайте текст теоремы. Там такое, кажется, не рассматривается. И таки три с учетом "multiplicity" , потому что x^3 = (x-0)*(x-0)*(x-0).
И да, вы опять начали рассказывать про несоответствие моих неформальных высказываний общепринятой теории, хотя разговор был про самосогласованость моей "теории".
Если в вашей теории действуют стандартные правила сложения и умножения, то начиная плясать от них, "основная теорема алгебры" легко доказывается. Корня должно быть три. Значит, какие-то внутренние противоречия у вас есть.
Я не вижу в ваших формулах ту неизвестную величину, которую нужно найти.
Это вообще-то значение x. Это выражения вида 2^3 = 8 при рассмотрении уравнения x^3 = 8.
Корня должно быть три.
(1/2 + i^9 *sqrt(3)/2) это тоже корень. Вы можете сколько угодно считать, что это не является решением, только при применении например в физике вращений может быть сколько угодно, и вам надо будет это учитывать.
(1/2 + i^9 *sqrt(3)/2) это тоже корень.
Только после очевидных упрощений это величина оказывается тождественно равна одному из трех разных известных корней уравнения x^3+1=0, а именно 1/2 + sqrt(3)/2*i. Вы еше скажите, что после кругосветки по экватору вы попадете не в начальную точку маршрута.
Я вам на это уже ответил. С какой целью вы повторяете одно и то же?
Все три корня x^3 = 0 тождественно равны, но считается, что это 3 разных корня. Вот и у меня считается, что это разные корни.
"после кругосветки по экватору" у вас будет одна кругосветка по экватору. Иногда это имеет значение. Если эта "кругосветка" создает какую-нибудь электродвижущую силу.
Общий случай a^b, где a, b — комплексные числа, определяется через представление в показательной форме согласно определяющей формуле:

Если хотите, можете считать, что в рамках моей теории это тоже называется "корень уравнения", поэтому в рамках моей теории их бесконечно много. Разговор был про отсутствие самосогласованности моей теории, то есть про несогласованность ее положений, а не про ее соответствие другой теории. Вы примеров такой несогласованности не привели.
Вообще в поворотах есть прямой смысл, связанный как раз с исходной задачей, из которой мнимые числа и появились. Как извлечь кубический корень из комплексного числа? Это ведь нужно в формуле Кардано.
Использовали метод неопределенных коэффициентов, а тут есть прямой способ - нужно осуществить трисекцию угла.
На самом деле есть два разных , одно является комплексным числом, а второе является символом, используемым для записи комплексных чисел в алгебраической форме.
Ага, примерно как два разных 2: одно является натуральным числом, а второе - символом, используемым для записи натурального числа в десятичной системе:)
Какой только чуши не придумают для "облегчения" обучения...
Совершенно верно, есть число 2 и есть цифра 2 и это разные штуки. А ещё есть запись числа 2 в десятичной система и это уже не цифра, а строка цифр (в данном случае состоящая из одной цифры), такая запись не является ни числом, ни цифрой.
есть число 2
Покажи?
и есть цифра 2
А вот это легко.
Ты это школьникам или первокурсникам объясни, умник. Для использования просто i удобней, но вот в целях обучения лучше писать 1i^1, вот когда концепция комплексных чисел в голове уляжется, далее можно сказать что проще просто i
1i^1
Так чего останавливаться, давайте сразу 1*1*(2-1)*1*(3-2)*i^1^1^1^1. Исключительно в целях обучения:) *facepalm*
Дайте угадаю, ни школьникам, ни студентам вы ни разу не преподавали, так?
Нет, не преподавал. А сколько из них реально понимают ваши объяснения? Если есть записи ваших лекций - киньте ссылку, если это хоть чем то отличается в лучшую сторону от того как эту тему преподавали нам я извинюсь и признаю что тот кому преподавали ничего не может говорит о преподавании тому кто преподавал.
Записей лекций у меня нет. Все, кто хотят понять - понимают. Конечно, есть такие которым пофиг. Ну, им уже ничем не поможешь.
Вот запись неплохой лекции. Я примерно так же рассказываю, с +- небольшими изменениями.
Только дошли руки посмотреть, сами понимаете - праздники. Эта лекция действительно оказалась несколько лучше того как преподавали нам, у нас она больше выглядела в духе "вот i , вот формулы, живите с этим", тут я хотя бы понял зачем нужна трегонометрическая форма и как естественно из этого вытекает ее применение в электротехнике.
Прошу прощения что сомневался в вашей компетентности и вынужден признать что тот кому преподавали ничего не может говорит о преподавании тому кто преподавал.
Само существование i упирается в минус и корень. Решил посмотреть, а что происходит, если попытаться взять корень из отрицательного числа и понял что все варианты решения это либо приближение, либо перебор. Выходит нет способа найти корень с абсолютной точностью кроме перебора?
Нельзя так писать. Для символа не определено возведение в степень, как и любые другие операции. Следует писать
-- записи именно такого вида являются комплексными числами.
Ты это школьникам или первокурсникам объясни, умник.
А ведь в погибшей цивилизации вполне себе успешно объясняли!
— бывший школьник погибшей цивилизации.
Вы же не считаете унарный минус в "-1" элементом.
Это на самом деле , просто в какой-то момент всех задобало постоянно писать символы (, 0 и ).
Точнее даже: solve( x: x + 1 = 0 )
Унарный минус можно считать частным случаем бинарного с заданным аргументом, но обычно бинарный минус определяют через унарный, то есть вычитание вводят как сложение с отрицательным числом. В геометрическом смысле унарный минус связан с изменением направления.
А также (1-2), (2-3) и так далее.
i = (0, 1) это некорректная запись
Именно что корректная. Потому что комплексные числа это как раз пары вещественных чисел с поэлементным сложением, ассоциативным и коммутативным умножением, таким что (1,0) x (1,0) = (1,0), а (0,1) x (0,1)=(0,-1). Точка. А запись вида 3+4i это просто математический сленг. тройка, это сокращенная запись 3x(1, 0)=(3,0), i это (0, 1), т.е. 4i это 4x(0,1)=(0,4), а исходное комплексное число именно что (3,4).
Вы не поняли, о чем речь. Запись некорректная, потому что i это операция.
Так же как "* = (0, 1)" или "+ = (1, 0)". Эти записи некорректные.
Можно записать "+1 = (1, 0)", но не "+ = (1, 0)".
Да, точку на плоскости тоже часто обозначают буквой i. Это и добавляет путаницы и непонимания, откуда берется -1.
i это операция.
Любая операция - это отображение. Одного множества в это же или другое. Я уже устал спрашивать, в какое?
Так же как "* = (0, 1)" или "+ = (1, 0)". Эти записи некорректные. Можно записать "+1 = (1, 0)", но не "+ = (1, 0)".
Прошу прощения, а вот этих формул я напрочь не понял. Что слева, что справа? Что означает знак равенства?
Я же написал, что они некорректные. Что вы хотите понять в некорректных записях?
Именно это же я подразумевал в комменте выше. i сам по себе можно считать аналогом унарного плюса и минуса, только он показывает другую ось. Если обозначить поворот на -90 градусов символом j, то единицы на всех 4 осях будут "+1, i1, -1, j1".
в какое?
А мы про какое говорим, по-вашему? Множество точек комплексной плоскости.
Что вы хотите понять в некорректных записях?
Вы в предыдущем сообщении написали, что:
Можно записать "+1 = (1, 0)"
Повторяю вопрос:
Что слева, что справа? Что означает знак равенства?
Слева "+1", положительное число на оси действительных чисел. Справа (1, 0), то же самое положительное число на оси действительных чисел, при рассмотрении ее в составе комплексной плоскости. Знак равенства означает, что можно считать, это то же самое положительное число.
Если вам непонятно, нарисуйте комплексную плоскость и обозначьте единицы на осях, покажите рисунок тут, я вам объясню в ваших терминах. Ведь для себя вы будете знать, почему вы обозначили их так, а не иначе.
Вот, теперь понятно.
Если вам непонятно, нарисуйте комплексную плоскость и обозначьте единицы на осях, покажите рисунок тут, я вам объясню в ваших терминах. Ведь для себя вы будете знать, почему вы обозначили их так, а не иначе.
Спасибо, мне геометрический костыль не требуется. ОТО в свое время отучила. И я тут, кажется, ничего не обозначал, кроме общеизвестных/общеупотребимых "истин".
Что вы хотите понять в некорректных записях?
Ну, например, логику воспалённого мозга, который их породил?
Зашёл после празднования НГ попуститься, ребята, двести сообщений, половина примерно о том же самом...
Andy_U абсолютно прав. Комплексные числа это упорядоченная пара (x, y), которая так же может быть записана как x+iy.
i никакой не оператор, это, если угодно слэнг, но точнее синтаксический сахар для удобства записи, в первую очередь, тех комплексных чисел, у которых либо (x, 0) = x, либо (0, y) = iy.
И ещё раз, это не оператор, это не функция, это не константа, это просто обозначение.
Еще раз, я не говорил, что в общепринятой математической теории это оператор. Я сказал, что понятнее будет считать его оператором. Причем я сказал это, чтобы не вводить новых обозначений. Если вам это непонятно, выше я предложил другой подход вообще без i: "ai^b = a⟲b". В этом случае можно продолжать обозначать точку (0, 1) как i, только смысла в этом никакого нет, она ничем не отличается от других точек на той же плоскости. Как это и должно быть.
Если "это просто обозначение", покажите как из этого обозначения найти декартовы координаты комплексного числа i^(1/3) (точки на комплексной плоскости). В вашем подходе это просто невозможно.
Это не какой-то мой подход, это строгая формализация понятия комплексного числа Уильямом Гамильтоном в далекой середине 19 века и это формальное определение живет с нами и ныне. Мистифицировать мнимую единицу больше нет ни одной причины с тех пор.
Уравнение x * x + 1 = 0 не решается, если x из ℝ
А вот в ℂ живут "другие" числа, те самые упорядоченные пары (x,y), и тогда уравнение пробретает вид (x,y)*(x,y)+1=0 и оно имеет два решения... Но не спешим, вспомним определение операций сложения и умножения в ℂ:
(x1,y1)+(x2,y2)=(x1+x2, y1+y2)
(x1,y1)⋅(x2,y2)=(x1x2−y1y2, x1y2+x2y1)
Это именно определения, созданные для удовлетворения двум целям, при отсутствии "мнимой" координаты они полностью эквивалентны таковым операциям из ℝ, что позволяет строить комплексные числа как расширение коммутативного поля ℝ.
Теперь наше уравнение можно просто раскрыть по определению операций, получая систему двух уравнений, которые имеют решения: (0, 1) и (0, -1), да-да, можно записать и как i и -i. А не издеваться над собой с определением, что i = ± sqrt(-1)
То, что ℂ - алгебраически замкнутое поле (извините, но только тезисно пишу) это прямо-таки ключевой фактор того, что вообще комплексные числа как бы "напрашивались" чтобы их ввели тем или иным способом, а вот геометричность их представления на плоскости это несколько вторичный факт. Без сомнений классный, ну и в каком-то смысле даже повезло, что мы люди, хорошо умеем работать с плоскостью, лучше чем с 3д всяким.
А вот Эйлер работал с комплексными числами еще до формализации Гамильтона, и, полагаю, будучи человеком умным, не делал какой-то драмы из наличия мнимой единицы и ее обозначений, вместо этого, фокусируясь на полезных свойствах комплексный чисел, и создал ту самую формулу Эйлера, которая и поможет ответить на Ваш вопрос с поворотами. e^iθ=cosθ+isinθ
И тогда уже понимание того, что возведение комплексного числа в степень z^w=exp(wlogz) может быть выполнено через несколько формул не должно вызывать сомнений. А "поворот" просто частный случай этой операции. И оно, разумеется, никак не следует из определения комплексного числа, не является аксиомой, а формулам мы обязаны Эйлеру, который работал с менее формализованным представлением, но тем не менее их можно просто "взять и использовать".
В общем, спорить тут, по большому счету, конечно не о чем. Но и вводить свои операторы для удобства непонимания я бы не стал.
это строгая формализация понятия комплексного числа Уильямом Гамильтоном в далекой середине 19 века
Ну теплород тоже был формализован, но оказалось, что эта концепция не работает. А уж отрицательные числа считались невозможными еще в Древней Греции. По вашей логике, так и должно было оставаться, никто не должен посметь что-то менять.
вспомним определение операций сложения и умножения в ℂ
В 20 раз объясняю, я говорю о том, как показать наглядно, почему они такие, как это работает, и какая тут связь с произвольной степенью. Вы говорите "просто запомни", я предлагаю другой подход. Я просто детализирую понятие, что такое i.
и создал ту самую формулу
В 20 раз объясняю, я говорю о том, как показать наглядно, почему она именно такая и как это работает. Я не понимаю, с чем вы спорите. Я в курсе, что эта формула существует.
которая и поможет ответить на Ваш вопрос с поворотами
У меня нет вопроса с поворотами. Я прекрасно понимаю, откуда там синус и косинус.
Но и вводить свои операторы для удобства непонимания я бы не стал.
Давайте так. Какой ваш ответ, почему "i*i = -1"? Потому что Эйлер так сказал?
Какой ваш ответ, почему "i^(1/3) = √3/2 + i*1/2"? Какой ваш ответ, почему "(-1)^(1/3) = 1/2 + i*√3/2", и почему "-1" тут тоже является решением?
Я дам свои, потом сравним ответы и проверим, какой из них удобнее для непонимания.
Напоминаю, что разговор идет про объяснение темы тем, кто с ней не знаком, или недостаточно ее понимает. В названии данной статьи есть фраза "путь к пониманию комплексных чисел". Покажите свой путь.
Я не только объясняю почему "i*i = -1", я даже могу продать комплексные числа восьмиклассникам, так, что они захотят у меня их купить. Жаль, конечно, что за этой красивой идеей нет никакого моего вклада.
Вот уравнение x^2 = -1. Хорошие школьники знают, что такого числа не существует, потому что если x отрицательно, то его можно записать как -y, где y положительно, и тогда (-y)*(-y) = y^2 > 0. Школьник не обязан знать аксиому упорядоченного поля, с него и так сойдет.
Тогда я говорю, а давайте у нас число будет немного по-другому устроено, как пара (x,y) и уравнение превратится в (x,y)^2 = (-1, 0). Причем я ввожу только определение операций сложения и умножения, уже писал их выше.
Тогда при раскрытии квадрата (как умножение числа на самого себя) получаем уравнение (x^2 - y^2, 2xy) = (-1, 0). Тут уже только троечник не скажет, что если 2xy = 0, то x или y равно нулю. Попробуем x=0, уравнение превратится в (-y^2, 0) = (-1, 0). y^2 = 1, значит два решения: y = -1, y = 1. Попробуем y=0, получим x^2 = -1. А мы только что говорили, что такого числа не существует. Итого, у нас только два решения, которые записываются как (0, 1), (0, -1).
Да, (0, 1)^2 = (-1, 0), чисто алгебраически. Да, просто за счет только двух определений (сложения и умножения). Я не продаю мнимую единицу, я не говорю что она вообще нужна. Но мы уже работаем с комплексными числами!
Но тут тянет руку ленивый отличник, и говорит, дядя, так очень неудобно записывать числа, очень много скобочек, запятых, и я говорю, конечно, вы можете записывать (x,y) как x + yi. Сначала класс посмеется, но так запомнит идею лучше. Но тут придется еще раз напомнить, что мы как работали с скобочками, так в голове и работаем, просто i-шки теперь отдельно, а не-i-шки отдельно.
И та-да, у уравнения x^2 = -1 есть два решения x = i, x = -i. Почему i? потому что это удобная запись, сами же просили, меньше скобочек и запятых.
Даю в качестве домашнего задания решить уравнение x^2 = -5, решают по той же схеме и пишут x = +- sqrt(5) * i. Вот так i прерасно согласуется с другими числами.
(добавлено) Забыл-то на ваш вопрос ответить. Почему i*i = -1 тоже даю в качестве домашнего задания. Школьники помнят, что i это запись (0, 1). Соответственно считаем (0, 1)*(0, 1) с учетом определения операции умножения, подставляем 0 и 1 в нужные места формулы определения, и ура, получаем (-1, 0) как ответ. Вот и все.
А с (-1)^(1/3) уже придется подождать, пока школьники немного подрастут. Мы ищем такое число, что его куб равен -1. x^3 = -1. Много знаний, чтобы попробовать -1 как решение - не нужно. А вот чтобы понимать, что в алгебраически замкнутом поле многочлен имеет корней столько сколько его кратность... но вот не в обиду, но не только школьники этого не понимают. И третий корень Вы где-то систематически умалчиваете. Это-то и позволяет мне говорить прямым текстом о подходе, как удобном для непонимания. Прошу прощения, если что, и с Новым Годом!
пара (x,y)
Тогда при раскрытии квадрата (как умножение числа на самого себя) получаем уравнение (x^2 - y^2, 2xy) = (-1, 0)
уже писал их выше
А откуда у вас там минус-то взялся?) Почему именно минус, а не плюс?
Вот вам и непонимание. А именно это и есть главный вопрос в понимании темы комплексных чисел.
"Выше" вы их просто постулировали: "Вспомним определение операций сложения и умножения в множестве комплексных чисел". То есть вы пытаетесь объяснить, откуда при умножении берется -1, через правило умножения, в котором вы постулировали -1. Это тавтология.
Всё, дальше ваши рассуждения для изучающего тему бесполезны, он должен только запоминать аксиомы.
Итого, у нас только два решения, которые записываются как (0, 1), (0, -1).
конечно, вы можете записывать (x,y) как x + yi
у уравнения x^2 = -1 есть два решения x = i, x = -i
Из этих записей внезапно следует, что i это не точка (0, 1), а что-то другое, что применяется только ко второму компоненту в скобках.
Иначе надо "(0,1)" записывать как "x + y(0,1)", а ее как "x + y(0 + 1(0,1))", а ее как "x + y(0 + 1(0 + 1(0,1)))" и так до бесконечности. Опять непонятно, то мы скобки раскрываем с помощью i, то приравниваем ее одну к скобкам. Это число или способ записи числа?
с учетом определения операции умножения
Вот и все.
Ага, только вопрос был о том, откуда взялся минус в вашей операции умножения.
но вот не в обиду, но не только школьники этого не понимают.
А вот разговор как раз о том, почему не понимают, и как можно сделать, что было понятно.
И третий корень Вы где-то систематически умалчиваете.
А вот дело как раз в том, как узнать, что там есть третий корень, и почему их на самом деле не 3, а бесконечно много.
А с (-1)^(1/3) уже придется подождать
Вот-вот, ваш подход требует знать много аксиом.
Вы тут для объяснения написали много текста, и то объяснили не всё. А вот мои объяснения.
Hidden text
Почему "i*i = -1"?
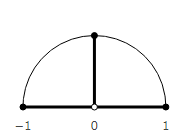
Можно считать, что умножение на i это поворот на 90° вокруг начала координат. "i*i" можно записать как "1*i*i", тогда получается, что мы поворачиваем исходную единицу 2 раза вокруг нуля. Так и получается "-1".
Почему "i^(1/3) = √3/2 + i*1/2"?
Можно считать, что степень i задает угол поворота. i в первой степени поворачивает на 90°, а в степени 1/3 будет в 3 раза меньше, то есть 30°. Как мы знаем из изучения тригонометрических функций, декартовы координаты этой точки "(√3/2, 1/2)". Аналогично можно вычислять любые другие степени i.
Почему "(-1)^(1/3) = 1/2 + i*√3/2", и почему "-1" тут тоже является решением?
Как мы показали выше, "-1" это поворот "1" на 90*2 = 180°. В 3 раза меньше это поворот на 60°, координаты равны "(1/2, √3/2)". Но если мы повернем "-1" еще на 360°, то тоже получим "-1". Это будет 90*6, а в 3 раза меньше это 90*2. То есть "(-1, 0)" это тоже правильный ответ.
Если мы добавим еще 360°, то получится 90*10 / 3 = 300°, это еще одна точка. Так как 360° можно добавлять бесконечно, то ответов тоже бесконечно много. В пределах 360° есть 3 ответа. Аналогично и для предыдущего вопроса, но обычно берут самый простой для вычислений.



По 2-3 предложения на каждый вопрос. Что проще понять людям, которые знакомы пока только с тригонометрией? Картинки приведены только для наглядности, их можно представить и в уме по описанию.
А вот дело как раз в том, как узнать, что там есть третий корень, и почему их на самом деле не 3, а бесконечно много.
А говорили, что ваша аксиоматика эквивалентна стандартной...
Можно считать, что умножение на i это поворот на 90° вокруг начала координат.
Это еще почему?
Во-первых, потому что это факт, можете проверить его в любом математическом пакете. Во-вторых, потому что так понятнее, почему получается -1 и все остальные результаты. Результаты правильные? Да. Значит можно так считать, значит подходы эквивалентные. Странно, что приходится объяснять математикам про эквивалентность.
Я бы посоветовал почитать труды Вейерштрасса, мне больше всего нравится в его подходе стремление в избавлении от интуиции в математике. Интуиция вещь тонкая, она и гениальных людей иногда в неправильную сторону ведет, а уж обычных людей так и подавно.
А откуда у вас там минус-то взялся?) Почему именно минус, а не плюс?Вот вам и непонимание. А именно это и есть главный вопрос в понимании темы комплексных чисел.
Ну я же уже это показывал:
(x1,y1)+(x2,y2)=(x1+x2, y1+y2)
(x1,y1)⋅(x2,y2)=(x1x2−y1y2, x1y2+x2y1)
Тут нечего понимать. Это не аксиома, не постулат, не теорема, это просто определение операций. Вот не было их до определения, ну не умели мы складывать и умножать числа из двух компонет. А ввели эти операции так. Школьнику надо просто запомнить. Смелому ученому мужу можно попытаться определить их по-другому, и получить вместо комплексных чисел какую-то обычно бесполезную структуру с другими свойствами, но это для другой части фильма.
Это как ln(x). Сначала его и вовсе не было, никакого, и никто никак его считать не умел (потому что его не было!). А вводится он так на вещественных числах: ln(x)=y, такой, что e^y=x для x > 0. Могли по-другому ввести, и по-другому назвать. Могли вообще не вводить, математика бы не исчезла, просто некоторые вещи бы записывались менее удобно.
Ну не интутивно умножение комплексных чисел, но тут можно только смириться. А если смирились, то ровно все по формулам, ни шага влево, ни шага вправо.
А как же не интуитивно то, что на упорядоченных тройках нельзя построить умножение без делителей нуля, а на четверках (кватернионы) можно, ух!
Всё, дальше ваши рассуждения для изучающего тему бесполезны, он должен только запоминать аксиомы.
Так а дальше никаких рассуждений и нет. Можно все остальное оформить как пару теорем и идти спать спокойно.
Из этих записей внезапно следует, что i это не точка (0, 1), а что-то другое, что применяется только ко второму компоненту в скобках.
Так вот так и есть на самом деле. Это не число, это маркер того, что все, что является коэффициентом при i является вторым компонентом в скобках упорядоченной пары. И любое число в такой записи может иметь ровно один компонент с i. По определению "(x,y) можно записать как x + yi".
Но в то же время, действительно i = (0, 1) при подстановке чисел в это определение. То есть записи
Иначе надо "(0,1)" записывать как "x + y(0,1)", а ее как "x + y(0 + 1(0,1))", а ее как "x + y(0 + 1(0 + 1(0,1)))" и так до бесконечности.
Тут что-то Вы уже куда-то не туда. (0,1) можно записать по определению как i. А вот x + y(0,1) это формально (x, y) или x + yi. Ну как, по каким определениям Вы их приравниваете? Не было таких.
Даже если просто идею поддержать, то да, мы можем записывать числа как 1+2+3+i-i+i-i, можем специально сокращаемые дроби на что-то еще домножать, в общем-то не очень математика здесь ограничивает. Но зачем?
А вот разговор как раз о том, почему не понимают, и как можно сделать, что было понятно.
А не знаю, это сложный вопрос. Про школьников, ну, обычно формулы дают с идеей "вы просто поверьте, а поймете потом". Ну будет формула Эйлера, будет комплексный логарифм и его многозначность. Все, сомнений нет, на правах постулатов.
Если им эта ваша математика зачем-то нужна, то в ВУЗе поправят все это добро через комплексный анализ. Когда ряды, интегралы уже из привычного мира, то в общем-то все нужные формулы выводятся вообще без тригонометрии, причем на строго доказательном базисе. Ну просто, это правда сложный вопрос, не понятно, какой бэкграунд считать обязательным, а какой побочным.
Вы тут для объяснения написали много текста, и то объяснили не всё. А вот мои объяснения.
Так а радости-то? Я "научил" хотя бы умножать комплексные числа, а Вы в самом частном случае их вращать. Осталось только понять, зачем их вращать-то вообще, если без умножения они как бы и не нужны-то вообще...
Да и такое, по большому счету, очень спорно:
Можно считать, что степень i задает угол поворота
Это тоже чисто из тригонометрии следует?
А самое вкусное-то и вовсе не в этом. А в том, что если пытаться строить какую-то структуру, которая
является коммутативным полем,
алгебраически замкнута,
полна в метрическом смысле,
содержит 𝑅 как подполе и операции согласованы
То с точностью до изоморфизма это единственно ℂ. И формула Эйлера неизбежно будет выполняться.
А структура такая нужна не для того, чтобы кружочки на плоскости рисовать, а для того, чтобы алгебраические уравнения решать. Мы так и хотели.
Когда вдумываешься в это, невольно прямо ощущается, насколько математика удивительна.
в избавлении от интуиции в математике
Я не говорю ни про какую интуицию.
Это не аксиома, не постулат, не теорема, это просто определение операций.
"Просто определение" это и есть аксиома. Когда вы вводите "X = Y", вы постулируете истинность этого равенства без доказательств.
Ну я же уже это показывал
Я знаю, что вы уже показывали. Я так и написал в предыдущем комментарии. Зачем вы это повторяете?
Школьнику надо просто запомнить.
А это вы зачем повторяете? Я уже сказал много раз, что цель моего подхода именно в том, чтобы не просто запоминать, а понять, вывести из более простой и наглядной концепции, из который выводятся и другие вещи.
Так а радости-то?
Осталось только понять, зачем их вращать-то вообще,
Я уже сказал много раз, затем, чтобы начинающим изучать тему было понятно, почему результат возведения в квадрат получается "-1", как это вообще можно представить. Что именно вам непонятно в этом объяснении?
До этого им говорили, что возведение в квадрат обычных чисел можно представить через площадь квадрата, которая неотрицательная, а тут вдруг появился минус в результате.
Я "научил" хотя бы умножать комплексные числа
Умножение в моем подходе как ни странно такое же, как в вашем.
Просто я минус не "ввожу так", и его не надо "просто запомнить", а он выводится наглядно из исходных одномерных действительных чисел.
После того как мы ввели, что "умножение на i выглядит как поворот на 90°", дальше можем делать любые умножения выражений "a+ib".
Что-то вы уперлись в свое вращение, хотя непонятно, что именно вращать-то, если у нас числовая прямая? Ну то есть вы просто с потолка взяли, что что-то там вращается, по мне, так это объяснение ничем не лучше. Почему вращается, почему именно настолько и почему в эту сторону? А обычные числа теперь как в квадрат возводятся? Что там вращается и насколько, что оказывается на положительной полуоси?
Что-то вы уперлись в свое вращение
Я "уперся", потому что мне продолжают и продолжают про него писать одно и то же, приходится отвечать. Высказывают претензии, что в статье "путь к пониманию комплексных чисел", в ответе на комментарий "новый подход к объяснению темы", в комментарии с фразой "для объяснения простой идеи" я посмел высказать неформальный подход к объяснению и не построил строгую математическую теорию, которая бы им понравилась.
А обычные числа теперь как в квадрат возводятся? Что там вращается и насколько, что оказывается на положительной полуоси?
А вот и подумайте, как число "-2" с отрицательной полуоси после возведения в квадрат оказывается на положительной.
Но в числе -2 нет i, а даже если и есть, то со множителем 0, что по вашим же словам означает поворот на 0 градусов (раз i это поворот на 90, а i/3 -- поворот на 30). Вот и объясните, как оно у вас поворачивается.
В числе -2 i находится во второй степени, это она и дает минус для исходного положительного 2. "По моим словам" вторая степень означает поворот на 180 градусов. Если мы его возводим в квадрат, степень i получается 2+2 = 4. Это 360 градусов относительно исходной положительной полуоси, то есть мы возвращаемся на нее. Дальше можете подумать, сколько будет "(-2)^2.1" и как расположены точки при движении от (-2)^2 = +4 к (-2)^3 = -8.
Но вообще я вам предлагал подумать, как это происходит в рамках ваших определений, а не моих.
вы пытаетесь объяснить, откуда при умножении берется -1, через правило умножения, в котором вы постулировали -1. Это тавтология.
Это у вас проблемы с пониманием логики и общеупотребительного математического сленга. Следите за руками:
Вначале мы определяем операции сложения и умножения для упорядоченных пар вещественных чисел. Операции сложения с вещественными числами и умножения производятся после предварительного преобразования вещественного числа X в (X, 0).
Далее, данные пары числе вместе с определенными выше операциями мы называем комплексными числами.
Проверяем, что пары (0, 0) и (1, 0) являются нулевым и единичным элементами в этом множестве. Далее мы будет просто использовать для их обозначения 0 и 1. Если стало уже невыносимо сложно, пишите 0z и 1z. Но можно и без трубы, как в известном анекдоте.
Теперь вводим обозначение i для комплексного числа (0, 1): i ≝ (0, 1).
Вычисляем i^2
≡i x i≡(-1, 0)≡-1z≡ -1(где -1 это комлексное число, такое что -1+1z=0).
Все. Где тавтология?
Я написал где в предыдущем комментарии - человек отвечал на вопрос "почему "i*i = -1"" и использовал в объяснении правила умножения, в которых уже постулирован множитель "-1". Он просто заменил одно выражение на другое более общее, а вопрос "откуда минус" остался.
вопрос "откуда минус" остался.
Из аксиоматического определения комплексных чисел, как упорядоченных пар вещественных чисел с заданными операциями сложения и умножения.
Если вы хотели спросить "почему", то тут ответ уже был - это единственный вариант, такой что для комплексных чисел вида (a, 0) математика совпадает с математикой вещественных чисел. Шаг влево, шаг вправо - попытка к бегству.
Из аксиоматического определения комплексных чисел
с заданными операциями
Вы играете словами, в этом случае вопрос превращается "а почему вам в аксиоматике удобнее использовать минус". Я объяснил это уже много раз.
это единственный вариант, такой что для комплексных чисел вида (a, 0) математика совпадает с математикой вещественных чисел
Вот дело как раз в том, что вы не можете объяснить, почему она в этом случае совпадает. А я могу.
почему "i^(1/3) = √3/2 + i*1/2"?
Потому же, почему диагональ квадрата 1 x 1 —
Без концепции вращения вектора это совсем не очевидно. "1^(1/3) = 1", а "8^(1/3) = 2". По аналогии можно предположить "i^(1/3) = i". Откуда тут вдруг какая-то сумма квадратов, которая должна быть равна коэффициенту перед i, который даже не написан.
Во второй части будет про геометрию. И там гораздо больше геометрического смысла, на самом деле, чем поворот.
умножение на i это операция поворота на 90 градусов.
Я просто оставлю это здесь
Текст и код усеяны юникодом, который для меня в большинстве случаев признак нейрообработки (и мне кажется не только для меня). Готов поверить, что вы это делаете сами -- в этом случае снимаю шляпу! Если же это всё-таки обработка LLM, то ... просто напишите что и где используете, люди поймут. Мне вот тоже иногда нейрослоп приписывают, думаю перестать тратить время на ручную замену "--" -> "—"
В данном случае нейронка была нужна для создания единой структуры и множества иллюстраций. К форматированию кавычек и тире я привык давно.
Скормил нейронке кучу книжек, вписал много чего, что нужно сделать, получил от нее версию плана, потом редактировал и добавлял тем еще, так через несколько итераций получил и продумал весь план целиком, ушло несколько часов на него (но тут важно то, что идеи такого цикла были уже давным давно. а весь материал мне известен, иначе бы так быстро не получилось). У меня есть детальный разбор каждого пункта плана, там можно все остальные 6 статей хоть сейчас мгновенно сгенерировать, но качество будет не то. Буду писать как эту первую часть все остальные. К тому же нейронка некоторые темы всё же пропускает, и не совсем то что нужно пишет.
К билдам — научился от нейронки сам недавно, выделения помогают чтению.
В тексте есть куски исторические, они просто выборочно переписаны с исторических книг, цитаты и формулы скопированы из них же.
А остальное — по сути есть в иллюстрациях этих, так что тут текст от нейронки не нужен был совсем. Вот даже это хваленого бота запускал, ничего не находит.
В статье по теории групп я сначала сделал текст от нейронки, потом переписал сам, бот что-то находил всё равно в небольших количествах, хотя это я просто вручную переписал с сохранением смысла своими словами. А тут писал текст сам полностью, признаков ИИ нет совсем.
Видимо, генерировать текст множеством промптов, а потом переписывать, идея не очень. Куда лучше генерировать структуру множеством промптов, чтобы нейронка сложила все нужные идеи в промптах, а также материал из пособий и статей в единую структуру, а потом заполнять самому эту структуру.

Эхх, а хотел поделиться статьёй. А тут опять ии. Стыдно должно быть за такое
У меня противоположный подход. Использование ИИ — признак качества сделанных материалов. Могу показать пример моего сайта
Вычислительная математика — Вычислительная математика
Весь сайт написан с помощью LLM. В результате этого работать с ним очень удобно — кладешь документ блокнот юпитер-ноутбук в папку, в нужном месте появляется новая страница. Всё настроено как нужно конкретному пользователю.
Все учебные материалы доведены до текущего очень презентабельного состояния именно с помощью ИИ.
Для иллюстраций, кстати. Обнаружил, что вместо того, чтобы мучать Gemini, лучше работает связка Дипсик + чатГПТ. Т.е. черновую версию иллюстрации кодом на Питоне делает Дипсик, он это быстро генерирует (Gemini ждать дольше), а потом закидываем в чатГПТ и тот за 2-3 итерации (иногда даже сразу за одну) иллюстрацию доделывает, у него это получается лучше, чем у Gemini.
думаю перестать тратить время на ручную замену "--" -> "—"
Вы её ещё и заменяете? А я вот не выйоживаюсь, а просто печатаю Alt+0151.
(Кстати, ™ — Alt+0153)
Да, а еще можно греческий алфавит, значок кубического корня и прочие прелести, но нет, спасибо, я пожалуй всё-таки лучше в
Так латех можно и в комментариях использовать??
Я для таких вещей использую msklc, работает прекрасно.
Некоторые элементы такого подхода можно найти в исторических книгах, но там, к сожалению, не ставят цели объяснить именно математику, там про ученых.
Для таких материалов абсолютно неважно откуда их получил автор. Это очень редкий и очень нужный тип работы. И выполнить его неимея в распоряжении нейросеть очень сложно. Я пробовал.
Современное описание комплексных чисел напоминает художественную летопись где реальная история порождает целый букет причудливо пересекающихся абстракций, отчасти принятых традиционно, но уже не достаточных. Это существенно мешает пониманию. Названия и пояснениядолжны образовывать целостный смысл.
Да и с нейронками сложно. Тут скорее речь о том, что довольно много разных знаний про комплексные числа накопилось уже, порылся ещё дополнительно в книгах и статьях, а нейронка позволяет это структурировать в единое повествование. А текст тут они не писали.
Кстати говоря, про связь комплексных чисел с группами и алгебрами Ли, про формулу Эйлера в любой ассоциативной алгебре нейронки вообще не вспоминают, если только напрямую им об этом не написать. Видимо, этого относительно мало в их обучающей выборке.
Я недавно буквально тем же но для для себя занимался. Закрывал детские гештальты). Пришел к интереснейшему выводу, для себя. О том что человечество переходит к осознанным описательным конструкциям в терминах состояний и переходов между ними.
Точнее - наш язык изначально оперирует состояниями, операторами и переходами из одного в другое. Он по сути таков. А разные подъязыки упрощают все это до формы, грубо говоря - современного учебника. Чисто из каких-то прикладных целей.
Начиная с комплексных чисел началась история затягивания этой сложной конструкции с состояниями - в науку, и замена ею чистых абстракций. Окончившаяся, на сегодня по крайней мере, судя по всему, гилбертовым пространством и тд. Интереснейшая и красивейшая тема, при этом многослойная.
Суток двое переписывался с ИИ и копался в других источниках. При том что сам ни разу не математик. Прост ради более целостной картины мира. Просто чудо что про это еще и пишут. Уверен что у 90 процентов выпускников стиль подачи материала в ВУЗах не оставляет и тени вопросов, котоыре могли бы привести к такому тексту.
И любая теория в физике, начиная с Ньютона, на категориальном уровне именно так и устроена (состояния, переходы и операторы).
Различие есть только между "монадами" (отдельными объектами) и полями. Первые описываются как объекты, имеющие небольшое число степеней свободы и свое пространство состояний, а вторые - клеточные автоматы.
Кстати говоря, нашел книгу Кардано автобиографическую. https://disk.yandex.ru/i/45pQzUAdh3s99g
Робофобская гидра пожирает сама себя, луддиты уже нападают на людей в тщетных попытках сдетектить ИИ. Продолжайте дискредитировать биошовинистов, ИИшникам это только на руку.
Тут еще фактически ввожу новую концепцию «отчужденного знания». По аналогии с Марксом.
Во второй части будет разобрано как раз подробно.
Сейчас пошло обсуждений этой статьи в соцсетях. Оказалось, многие не знают о том, что при возведении в мнимую степень происходит «обмен ролями»: модуль исходного числа влияет на угол поворота результата, аргумент исходного числа влияет на модуль результата. И много других геометрических вещей не знают, важных для понимания. Как раз вторая часть про это.
Тут еще фактически ввожу новую концепцию «отчужденного знания». По аналогии с Марксом.
В математике каждый термин несёт в себе какую-то собственную пользу. Отсылки к марксизму в виде утверждений, которые ниоткуда не следуют, и ни чего не объясняют, выглядят в этой статье как инородное тело. Да и сам он появился явно позже, описываемых здесь событий. Видно, что вам близка эта тема, но было бы лучше вынести в отдельную статью, чтобы можно было проследить всю логику.
Здесь весь план статей на цикл построен на основе определенной философии. Историческое развитие понимания комплексных чисел, совпадающее с описанными 7 стадиями. У Яновской похожее было сделано в объяснении понятия множества.
А в конце - на основе продемонстрированного подхода общая философия понимания.
Ну конечно, 7 стадий это что-то само собой разумеющееся. Поэтому не нужно ни чего объяснять, достаточно просто их перечислить. В 2025 же все изучают Маркса со школьной скамьи, в отличие от комплексных чисел.
Если серьёзно, аналогия с миром финансов заинтриговала. Однако в реальности для денежных расчётов не используют комплексные числа. Ну то есть будь у такой философии хоть какой-то практический смысл, мы бы видели эту математику на практике. Уж кто, а бизнес вряд-ли упустил конкурентное преимущество в оценке ценностей, будь оно здесь. Но это просто догадки, вероятно я не понял эту часть статьи.
Видимо, стоит вообще в начале второй статьи раскрыть, а не в конце цикла, там логичнее, да и смыкается такой переход с концом этой статьи логично. Суть в том, что мнимая единица прошла такой исторический путь:
Артефакт вычислений.
Формальный символ одной операции.
Случайный, но полезный инструмент.
Систематический используемый с оформленными правилами работы, но непонятный
Геометрически осмысленный объект, полностью понятный.
Ядро собственной теории.
Часть всеобщего языка науки.
Это и соответствует этим 7 этапам.
В этой статье я раскрыл первые 4:
Кардано.
Бомбелли (и еще Декарт, кстати, можно было его тоже упомянуть).
Эйлер, Безу, Муавр и т.п.
Даламбер и прочие ученые в конце 18-го века. Там как раз та самая "революционная ситуация" - правила уже сложились, а понимания нет.
Пятый и шестой этап - это 19-й век, а седьмой этап - уже 20-й скорее (теория групп и алгебр Ли, применения в квантовой механике и тому подобное).
Считается, что вообще эту семичленку придумала Яновская, а не сам Маркс, но она на конкретных примерах есть у Маркса (деньги, товар, натуральное число, дифференциал). Просто Маркс не писал ее в виде явного списка нигде, кроме оглавления "Капитала".
У Яновской в статьях по философии математики есть анализ, почему это именно так устроено. Она была ученицей Колмогорова и тем самым человеком, который математические рукописи Маркса первым разобрал, перевел, оцифровал.
можете дополнить своё повествование о числах кватернионами. Тем более, что они как бы продолжение идеи мнимых чисел
Читаю первую же фразу:
«Квадратного корня из минус единицы не существует» — эта фраза, сказанная на уроке, становится ментальным барьером. Она возводит преграду «дальше не думай», за которой остаётся самое важное — вопросы «почему», «как» и «а что если».
Извините, а что у вас за школа была? У нас в школе объяснили очень просто: квадрат положительного числа положительный, квадрат отрицательного числа положительный (минус на минус), квадрат нуля равен нулю. То есть квадрат любого числа не может быть отрицательным. Объяснение занимает 1 минуту и всем понятно.
Как видите, никакой опереточной «преграды».
квадрат положительного числа положительный, квадрат отрицательного числа положительный (минус на минус), квадрат нуля равен нулю. То есть квадрат любого числа не может быть отрицательным.
...более того, На Самом Деле™ (то есть корня вообще-то два).
По определению, корень - неотрицательное число. Не нужно путать с корнями уравнения `x*x - a*a = 0`
Это зависит от определения. В школе определяли как «число, которое надо возвести в указанную степень, чтобы получилось подкоренное выражение».
Это вы про какую-то "неправильную школу" говорите. Если принять ваше определение, то нельзя сказать верно или неверно такое неравенство

То, о чем вы говорите, называется "арифметический корень". Он может быть только положительным. А просто "корень" - любым. И да, это стандартные школьные определения.
Да, но это ничего не меняет. Отрицательное число можно возводить в квадрат и получать положительное (про это как раз ваш пример). Но какое число не возводи в квадрат, отрицательное не получится, даже с многозначной функцией корня.
Ну раз все квадраты положительные, то корень из отрицательного числа не имеет смысла, то есть его не существует. В чем ваше объяснение противоречит статье?
Ну и отдельный вопрос: i положительно или отрицательно? В статье, кстати, рассмотрен.
Нам в школе объясняли, что вводить i через квадратный корень - не корректно. Комплексные числа вводились как пары чисел с определенными свойствами, из которых следовало i^2 = -1 Это корректная записать без использования квадратного корня.
Квадратный корень - это буквально решение такого уравнения. Так что от формы записи ничего не меняется.
Нам в школе объясняли, что вводить i через квадратный корень - не корректно.
Да. И совершенно правильно говорили. Строго говоря, надо спросить: который из? Потому как в области комплексных чисел корни из единицы распределены на окружности, то есть — их некоторое множество. А ещё есть аргумент комплексного числа. Опять же: который из?
А дальше возникает идея и понятие римановой поверхности и римановой (многолистной) функции. Жалко, что такие красивые вещи не изучаются прямо в школе, когда мозги ещё быстры и податливы. Можно было бы потом заняться наукой и получать глубокие результаты.
Не корректно, потому что √-1 = i и √-1 = -i, так как √ это многозначная операция.
То есть значение i для математики похоже на значение бога для верующих? Типа, какая разница существует ли он где-то или нет, все равно через него можно описывать и разрешать что-то новое?
Комплексные числа это как переход на новый инструментальный уровень. Теперь у вас есть число на плоскости, пространство, вектора, и даже матрицы можно приплести. Ничего сверхъестественного, просто эволюция математического аппарата.
какая разница существует ли он где-то или нет, все равно через него можно описывать и разрешать что-то новое?
Так с любыми математическими понятиями. Комплексные числа тут абсолютно никак не выделяются.
Так с любыми математическими понятиями
Это только сейчас так. Раньше было иначе.
Комплексные числа тут абсолютно никак не выделяются
Выделяются. В самом названии "мнимые числа" уже указано их отличие от натуральных и действительных.
В те времена философия была такая, что числа "отражают" Природу. То есть числа не "придумывают", а "открывают".
Это касалось не только чисел, но и геометрии. Геометрия должна "отражать" Природу, поэтому Лобачевского и травили, а сам он мерил углы в актовом зале своего Универа в надежде, что его геометрия верна(!) на больших растояниях.
Да, но какая разница, что там было или не было раньше? Если копаться во всей этой заплесневелой истории - времени на современные вещи не останется. Лучше сразу прививать себе взгляд на вещи, который позволит изучать математику наиболее продуктивно. И попытки вытащить глубокий "философский" смысл из названий типа "мнимые", "действительные" и т.д. - только отдаляет от понимания сути вещей.
И попытки вытащить глубокий "философский" смысл из названий типа "мнимые", "действительные" и т.д. - только отдаляет от понимания сути вещей.
Так оно конечно, - зубрим, решаем задачки и сдаём экзамен - это практично. Чего ещё делать то? - но разве это понимание?
Наверняка для понимания нужно знать историю появления этого понятия. Иначе наука превращается в набор "табуреток".
Так что для понимания нужно наверняка знать- с какого бодуна появилось название "мнимые".
Это касается не только математики, но и остальных наук. Например, почему физикам удалось переиначить "волновую механику" в "квантовую механику", но не удалось такое же провернуть с "волновой функцией".
Иначе, да - зубрёжка и только зубрёжка.
Вспоминаю как на 2- курсе началась Теоретическая Механика и препод сходу написал Лагранжиан на доске. И всё! - вся Общая физика (школьная и на 1 курсе вуза), такая понятная, внезапно рассыпалась в прах.
А препод не стал пояснять, откуда и зачем взялся этот Лангражиан и что это вообще за штука такая. - вызубрили и сдали, но поняли ли?
P. S.
"Табурет от французского «tabouret»,что буквально означает «барабанчик».
Слово «табуретка» происходит от французского «tabouret», что изначально означало круглую подушечку для иголок или пуфик, а позже стало обозначать низкий стул без спинки, заимствованное через немецкий язык в русский, имея ассоциации с мягким сиденьем или барабанчиком. Изначально это была привилегия при французском дворе, символ статуса, а затем стала обыденным предметом мебели."
Вот, кстати, с табуреткой хороший пример. Для понимания того, что такое табуретка, совершенно не нужно знать всю эту этимологию, или историю табуретки вплоть до французского средневековья. С математикой точно так же.
А препод не стал пояснять, откуда и зачем взялся этот Лангражиан
Откуда и зачем взялся - прекрасно объяснено буквально на первых же страницах первого тома ЛЛ. Кто ж вам виноват, что вы их не читали. И совершенно непонятно, что может добавить к этому пониманию знание того, кто и в каком году его вывел.
Общая физика (школьная и на 1 курсе вуза), такая понятная, внезапно рассыпалась в прах.
У меня, кстати, наоборот: после теормеха (и других теор. курсов) по ЛЛ разрозненная мешанина общей физики наконец сложилась в единую стройную систему:)
Откуда и зачем взялся - прекрасно объяснено буквально на первых же страницах первого тома ЛЛ
Нет. Там типа "В механике вводится функция, называемая лагранжианом, такая, что действительное движение системы определяется условием экстремальности действия".
Это можно назвать "инженерным пониманием", когда дают формулу и учат как решать уравнения. И не более. Ни истории, ни как это возникло и почему именно так принято записывать, а не иначе. И чем это лучше описания не через уравнения сил.
Формула "падает с неба" на доску преподавателя и всё. - это типичное "инженерное понимание" любого явления.
"В механике вводится функция, называемая лагранжианом, такая, что действительное движение системы определяется условием экстремальности действия".
Так это и есть объяснение. Функция Лагранжа выводится из принципа наименьшего действия. Если вам нужно обоснование, откуда берется принцип наименьшего действия, то его нет. Он просто угадан так, чтобы результаты расчетов соответствовали результатам экспериментов.
Ни истории, ни как это возникло и почему именно так принято записывать, а не иначе.
Ну, если вам так уж зачем-то нужна история, то никто не мешает вам в свободное время пойти в библиотеку и штудировать там труды Лагранжа (или Гамильтона, или Эйлера, или хз кто там первый это записал). Но в обязательном курсе - это только отнимает время впустую, ничего не добавляя к сути.
И чем это лучше описания не через уравнения сил.
А вот это проясняется на семинарах, где задачи, которые решались бы очень сложно через законы Ньютона, решаются в одну строчку методами вариационного исчисления. Ну и в дальнейших курсах теорфизики также.
На вопрос откуда принцип наименьшего действия, ответ состоит из двух частей.
Во-первых, это связь между диффурами и экстремальными задачами.
Во-вторых, есть большая история вариационных принципов в разных разделах физики, и там везде они несут физический смысл.
Во-вторых, есть большая история вариационных принципов в разных разделах физики, и там везде они несут физический смысл.
Само собой. Но это не ответ на вопрос "откуда взялся ВП?". Это иллюстрация его применения. Ответ на этот вопрос я привел выше:
Он просто угадан так, чтобы результаты расчетов соответствовали результатам экспериментов.
А так да, практически вся физика - это развернутый пример применения вариационного принципа к различным ситуациям.
Нет, принцип наименьшего действия не угадан, он выведен.
Сводить всю физику к вариационному принципу неверно.
В ландавшице в разных разделах физики этот приём - подбирается действие, потом варьируется. Но на самом деле просто по известным уравнениям было подобрано действие, которое их даёт, а не наоборот. Так что такие выводы по Ландау можно рассматривать как некоторый концептуальный обман.
То есть смотрите как происходит.
Есть экспериментальные данные, на основе них выводятся уравнения.
Эти уравнения дальше анализируются, обобщаются, усложняются в том числе на основе разных физических принципов (сохранение энергии, ковариантность, относительности, причинность, обратимость и так далее).
А потом из уравнений выводят действие, экстремум которого даёт эти уравнения.
Преимущество подхода с действием в том, что по форме действия очевидны симметрии, которыми обладает уравнение. А по форме уравнения эти симметрии куда менее очевидны.
А ещё, записывая действие, можно выводить инварианты сразу по теореме Нетер, минуя теорию групп и анализ группы симметрии
Есть экспериментальные данные, на основе них выводятся уравнения.
Ну, вот об этом я и говорил.
А все вот это:
Эти уравнения дальше анализируются, обобщаются, усложняются в том числе на основе разных физических принципов (сохранение энергии, ковариантность, относительности, причинность, обратимость и так далее).
теорию групп и анализ группы симметрии
может и хорошо для дальнейшего изучения, но абсолютно не подходит для начального курса теорфиза. Потому что чтобы осознать и оценить все эти манипуляции - нужно уже очень хорошо знать, что такое уравнение Эйлера-Лагранжа, лагранжиан и вообще иметь неплохой такой уровень математики и опыт в занятиях теорфизикой.
Формулу для действия можно получить как подбором через уравнение Эйлера-Лагранжа, так и напрямую через механику Гамильтона (там есть явная формула через гамильтониан).
Но в ландавшице этого нет. Для начального курса теорфиза, возможно, принцип наименьшего действия вообще лучше не использовать, чтобы не запутывать людей.
Приведу пример такой яркий. Уравнение Шредингера - это на самом деле частный случай уравнения Гамильтона-Якоби. И в его выводе есть много физического смысла, и там целая история есть поучительная, откуда оно взялось.
В Ландавшице вместо этого вот это

Откуда взялась сама Пси, понять конечно невозможно, и, разумеется, это всё чистый подгон под ответ вместо вывода.
Для первоначального изучения теорфиза курс Ландау категорически не подходит.
Подход Ландау чисто инженерный - как можно быстрее дать готовый аппарат для решения актуальных задач (а это как раз вариационных подход, теорема Нетер и тому подобное) , не заморачиваясь с пониманием основ, смысла.
Для первоначального изучения теорфиза курс Ландау категорически не подходит.
А что подходит? И зачем тогда он нужен?
Курс Ландау был нужен, чтобы наиболее одаренных в СССР студентов быстро научить решать актуальные научные задачи, отфильтровав менее одаренных (они не справятся просто).
Собственно, сам Ландау этого не скрывал, что цель его курса - отбор самых лучших, "испытание на прочность", а не обучение.
Более того, он же поставил еще второй фильтрационный барьер, в виде того самого теорминимума Ландау.
А для обучения теорфизу гораздо лучше использовать, например, американские учебные курсы и учебники.
По квантам не знаю, не читал. А вот для механики первый том - самое то что нужно для начального знакомства.
Подход Ландау чисто инженерный - как можно быстрее дать готовый аппарат для решения актуальных задач (а это как раз вариационных подход, теорема Нетер и тому подобное) , не заморачиваясь с пониманием основ, смысла.
Смысл формируется на основе решения кучи задач, а не наоборот. Так что это как раз правильный подход.
Механику по Ландау считается вообще невозможно изучать, поэтому нигде и не изучают. Рекомендуется как дополнительное чтение после семестрового курса аналитической механики.
Более-менее можно изучать по Ландау первично только теорпол и кванты, и так изучают, но это довольно плохой выбор.
Смысл формируется в результате разбора и использования теории. Задачи можно решать и без размышлений о том, как там теория используется, в таких случаях решение задач смысл не формирует, и в большинстве случаев так и происходит - навык нарабатывается, смысла за ним нет.
Если брать людей с инженерным образованием, даже с красным дипломом, там в основном не осталось у них никакого смысла после математических курсов, только некоторые навыки.
Т.е., проще говоря, они несколько лет изучали много математических курсов, решали очень много задач (как на этих курсах, так и на технических предметах, где математика применяется), но даже основы первого семестра не поняли, и это типичная ситуация.
Смысл формируется в результате разбора и использования теории.
А "использование теории" - это и есть решение задач. Без этого можно хоть обчитаться теории - понимания не добавится. Максимум - может появиться иллюзия понимания.
В довольно редких случаях это так. Обычно используются методы решения задач, довольно отдаленно связанные с теорией.
но разве это понимание?
Это порождает понимание.
Ну не знаю, а что есть в природе в виде однозначной пускай даже единицы? Что б вот не было сомнений где граница одиночного объекта или величины?
Людей часто травмируют комплексные числа, но почему-то никогда не травмирует число 2.
Хотя оно такое же абстрактное.
корень из двух в свое время довольно сильно травмировал древних греков.
но почему-то никогда не травмирует число 2
Его можно на пальцах показать. Маленький ребёнок, который ещё считать не умеет, вполне может представлять себе, что такое "два".
Число i более абстрактное чем 2, оно более отрешённое от реальной жизни.
На плоскости комплексные числа вполне себе упорядочиваются. В действительных числах корня из отрицательных чисел действительно не существует. Комплексное число называется "комплексное", потому что мы оперируем парой чисел как единым целым. Мнимая единица - это просто символ, позволяющий оперировать парой чисел как единым целым алгебраически. Оперировать комплексными числами можно и в матричном виде, но это не так удобно. Элементарные функции комплексного переменного определены везде и выводятся через их разложение в степенной ряд.
Факты just for fun:
(простое число)
(значение косинуса больше единицы)
Хорошо написано, но нет времени все читать. Маленькие добавки:
Вопрос о физическом смысле мнимой единицы у тех, кто ею пользуется, никогда не возникает. А вот для отрицательных числе хорошо бы придумать объяснение, в физике же (время, расстояние, масса, температура) их нет.
Для широкого практического применения (цифровой обработки сигналов) студентами и инженерами хорошо бы придумать физическое (не математическое) объяснение периодичности цифрового спектра и того факта, что можно взять любую инверсную копию спектра (в том числе, из минус бесконечности) и восстановить по ней реальный физический сигнал.
в физике же (время, расстояние, масса, температура) их нет.
Координаты векторов. Знаки электрических зарядов.
Всё зависит от точки зрения - векторы всегда положительные, только расположены в разных местах и смотрят в разные стороны. А ярлык "отрицательный" - проявление субъективизма человека. Можно же было назвать разные заряды красными и синими... Мужчины и женщины тоже притягиваются, кто из них отрицательный?
Можно было. Поэтому названия ни на что не влияют. Можно называть "красный" и "синий", можно называть как угодно, хоть табуреткой. Главное, корректно ввести операции на этих объектах. В этом и суть математики: в соответствующих структурах, а не в названиях.
векторы всегда положительные
Что значит "положительный вектор"? Это что-то новенькое.
... не забыв сообщить заинтересованному читателю о необходимости иметь достаточную частоту дискретизации (теорема Котельникова!). Ну и, конечно, восстановить можно не всякий сигнал, а только сигнал с ограниченным спектром (опять же: теорема Котельникова и частота Найквиста!)
У теоремы Котельникова с физическим смыслом всё хорошо. А вот сигналов с ограниченным спектром не существует. С физическим смыслом здесь проблем нет, но его нужно проговаривать и объяснять следствия
Согласно теории относительности, взаимодействия выше скорости света быть не может. Соответственно в реальной жизни абсолютно все сигналы - с ограниченным спектром.
Сигналы с ограниченным спектром имеют бесконечную длительность. А в нашей вселенной это невозможно
Ну это опять же только если принимать бесконечную делимость пространства. Что значит наличие некоторой амплитудной полки, ниже которой опуститься невозможно.
Вопрос о физическом смысле мнимой единицы у тех, кто ею пользуется, никогда не возникает. А вот для отрицательных числе хорошо бы придумать объяснение, в физике же (время, расстояние, масса, температура) их нет.
Я пользуюсь мнимыми числами (цепи переменного тока, ТАУ), но физический смысл их так и не уложил в голове. Объяснил себе, что это просто удобная математическая абстракция для отражения некоторых явлений и вычислений. Также как и матрицы в линейной алгебре. А в чём проблема с отрицательными числами не понятно. Координаты, скорости, ускорения. Угловые и линейные. Если поворот вправо на 5 градусов это +5, то поворот влево на 5 градусов это -5, что тут объяснять?
у тех, кто пользуется, проблем нет. Статья же о том, как объяснить другим. А отрицательных числе в природе (в физике) просто не существует. деление чисел на положительные и отрицательные - как выбор правостороннего и левостороннего движения
в физике же (время, расстояние, масса, температура) их нет
Отрицательная температура (в каком-то смысле ниже абс нуля) – вполне себе устоявшаяся концепция для термодинамики неравновесных систем. https://en.wikipedia.org/wiki/Negative_temperature
Рабочее тело лазера в момент накачки вполне можно как пример такой системы рассматривать.
Тут главный вопрос «что считать временем, массой и температурой», а не «бывает или нет».
Можно считать всё, что угодно, главное - договориться считать одинаково. А если объяснять что-либо постороннему, полезнее исходить из его понимания.
договориться считать одинаково
Так не получится же. Масса – как синоним веса – работает при невысоких скоростях на макрообъектах, но чуть в микромир или в быстрое перемещение, начинается чёрте что. Температура может быть мерой «тёплости», статистикой скорости, статистикой спектрального распределения, статистикой распределения по уровням энергии частиц и тд.
Про расстояние и время даже начинать не хочется.
Если исходить из понимания… Легко сказать. «Понимание» – уже не про реальный мир, шире чем просто ощущения. Понимание – про интерпретацию ощущений, а поди угадай какое оно у конкретного человека. Людям и отрицательные числа, и комплексные заходят – но заодно и астрология, и тонкие тела, и вообще всё что хотите. Безотносительно оно бывает или нет.
в чем проблема сопоставить отрицательным числам дырки?
Маслов, например, вообще вводит отрицательные размерности в работе "Общее понятие топологических пространств отрицательной размерности и квантование их плотностей"
https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mzm&paperid=3530&option_lang=rus
А зачем? Можно ввести всё, что угодно, например, дважды мнимое 5-мерное квантованное пространство, если это даст полезный практический эффект. Но эффекта не вижу, поэтому не ввожу :).
Из круга подобных вопросов у меня вызывает некоторое неудобство только принятое положение, что ток течет от плюса к минусу. Я предпочитаю объяснять работу транзистора на примере n-p-n транзистора и мне было бы удобнее, если бы принятое направление тока совпадало с направлением движения электронов. Но соблюдаю принятые правила поведения.
Но соблюдаю принятые правила поведения.
И никто из нынешних конформистов совершенно не думает о будущих поколениях..
Никто же не знает, что будет удобнее будущим поколениям - может быть они будут считать постоянный ток в цепи стоячей волной, а не потоком электронов
Да-да, а сейчас ток - это поток дырок, которые электронная пушка затягвает в себя как пылесос.
В медном проводе, в эмиттере и коллекторе n-p-n транзистора дырок нет
</sarcasm>
А как всьерьез, но на пальцах, объяснить вытекание электронов из базы? Они же пали жертвой рекомбинации?
Сам сформулировал объяснение: 1% потока электронов, поступающих в базу из эмиттера, участвуют в рекомбинации (99% уходят в коллектор). Для изначально электрически нейтральной p-области базы это означает приобретение отрицательного заряда, но так как база подключена к положительному потенциалу, он забирает этот отрицательный заряд. Таким образом, базовый ток - это ток разряда пространственного заряда тела базы. Если этот ток прервать (отключить положительный потенциал), накопленный вследствие рекомбинации в базе отрицательный заряд выступит барьером на пути потока электронов из эмиттера и все токи прекратятся.
И это объясняет усиление базового тока в 99 раз - ток эмиттера устанавливается таким, чтобы 1% от него (при коэффициенте передачи эмиттерного тока в коллектор равным 0,99) поддерживал электрическую нейтральность тела базы.
Ни в одном учебнике я этого объяснения не видел
Поскольку , а значит
...куда исчез X?.. и в первом выражении и во втором (уравнении).
Автор ещё не дошёл до формулы Муавра. (Либо я что-то пропустил...) Операции над комплексными числами позволяют получить явные формулы для тригонометрических функций составных углов. Тут ещё имеется прямая связь с задачами на построения при помощи циркуля и линейки.
x^3+xa=b. Вы говорите про замену х=b-a а потом откуда взялось это здоровенный уравнение, если мы сделали замену, то иксы вообще уйти должны были. Ниче непонятно, вас не только кандидаты математических наук читают, ну почему всегда так!
Статья из серии "Сложно о простом". Это точно не туториал. Если это науч-поп или исторический экскурс, то слишком перегружено.
С помощью комплексных чисел работает Wi-Fi, обрабатывается аудио и видео, функционируют законы квантовой механики
Законы квантовой механики все-таки описываются с помощью комплексных чисел, а не функционируют. Понятно что это урок по математике, а не по русскому языку, но все же.
Приглашение к бунту. «Квадратного корня из минус единицы не существует»
Корень из отрицательного числа "невозможен" только в рамках арифметики. Получается что это бунт против арифметики.
На мой взгляд, говорить, что комплексное число — это поворот, некорректно.
Нужна отдельная глава, поясняющая чуть математических объектов (конструкций), как устанавливается и какая связь между ними (например, комплексное число и повороты, повороты и теория групп, теория групп и симметрия), что значит конструкт применяется к реальному миру (кастрюля, конечно, цилиндрическая, но в цилиндре суп сварить нельзя).
Планка взята очень высоко, поэтому аккуратность и скрупулёзность на понятийном уровне критично важна.
Поэтому желаю успеха и не потерять задора и энтузиазма в этом деле.
Ещё одно замечание. Материал полиаспектный и каждому читателю нужно (заходит) что-то своё. А текст, увы, линейный, пусть и имеет иерархическое разбиение.
Я бы предложил подумать над типологией читателя и для каждого типа предложить свой маршрут по книге. Я такое встречал в некоторых монографиях, там в основном, по уровню подготовки и глубине интереса к вопросам, раскрываемых в книге. Грубо говоря, если вы это знаете, эти главы можно не читать. Если вы этим интересуетесь, прочитайте вот эти главы.
Иначе часть критики (совершенно справедливой) будет про "кому вы это пишите" и "зачем вы это написали".
А в СССР нас, шестиклассников, пытали вот такими вот занимательными книжками








(Лёвшин В. А., Александрова Э. Б. Путешествие по Карликании и Аль-Джебре. — М. : Детская литература, 1991. — 255 с. : ил. ISBN 5-08-001458-х.)
Надо посмотреть.
Со своей стороны порекомендую Гиндикина "Рассказы о физиках и математиках".
Там про комплексные числа тоже прилично написано.
У меня в детстве была занимательная книжка по математике, но название и автора, я, к сожалению, забыл. Помню, как самообучающийся компьютер из спичечных коробков клеил.
а иррациональные и трансцендентные числа никого не смущают? )))
каждый раз диву даюсь как вроде начинают с красивых формул а к концу статьи скобки начинают плыть, а корни торчат как символ. как у людей разметка-то ломается
Это где переписка математиков поплыли?
Их из исторической книги mathpix-м выдирал, могу переписать их нейронкой.
Их из исторической книги mathpix-м выдирал,
Как будто это что-то оправдывает
Тут дело в том, что это кажется нормальным (такие значки корня), потому что в старых книгах часто такое встречается.
В смысле кажется? Вы же пишите статью для обучения, и надеюсь, прочитали то, что (вам) понаписали?
Что-то у меня после этих ваших заявлений очень сильный скепсис по поводу выполнения вами поставленной цели объяснить математику просто. Для этого в первую очередь ляпов не должно быть.
Ляпов тут никаких нет. Использование знака корня перед скобками (например, √(ab+c) ) является общепринятым и стандартным в современной математической записи. Другое дело, что массовому читателю это может не понравиться, особенно тому, который не часто это встречал.
Как я и написал, взято это было из популярной книги по истории математики.
Так я писал про то, что у вас в тексте явно скобки поплыли (буквально -- открывающая висит в показателе степени, закрывающая на уровне основного текста), к чему относятся значки радикалов, непонятно, где была степень -- непонятно, в одном месте 6 в 36 кажется превратилось. Сейчас уже поправлено, но вы правда думаете, что с замахом "объясню сейчас все четко и популярно" смазанный текст сослужит хорошую службу? А оправдываетесь тем, что мол, OCR подвел. Ну так у вас для этого глаза же есть, чтобы за ним проверить?
Ведь первую статью так хорошо начинали, и вот, не успели двух шагов пройти, а уже скатываетесь.
да даже классика и та сползала. корень из минус единицы в половине случаев нормальный, в другой половине как UTF символы, степени в показтелях многочленов начинали степень открывющей скобкой которая закрывалась на уровне множителей подстепенного. щас правда уже не вижу тех формул почему-то, где-то что-то видимо подшаманили или удалили. да и классику починили вроде
Благодарю за статью!
Получилась прекрасная ода комплексным числам!
Хотел бы обратить внимание, что несмотря на все прелести комплексных чисел, невозможно сформировать пространство (алгебраическое тело) на этих числах. Возможны только комплексные алгебраические поля.
Эту проблему смог преодолеть Елисеев в работе "Теория функций пространственного комплексного переменного" http://www.vixri.ru/d/a_mat/Eliseev%20V.I._VVEDENIE%20V%20METODY%20TEORII%20FUNKCIJ%20prostranstv.kompleksnogo%20peremennogo.pdf
с помощью другой конструкции прямой. Он нулю сопоставил пустое множество и получил в нуле на прямой окрестность с выколотой точкой. В работе он это называет "дужкой". Получил нехаусдорфову прямую (если я правильно понимаю) и новые пространственные комплексные числа, которые образуют алгебраическое тело.
Спасибо, было очень интересно.
А когда выйдут остальные части статьи?
В январе все выйдут.
Нет, в феврале. Я делаю паузу сейчас, полно других дел появилось.
Вторую часть вчера дописал и отложил на 7 февраля, она в 2 раза больше первой вышла и концептуально сложнее.
К остальному вернусь в начале февраля.
Ни одного элемента в матиматике в природе нет. В этом отношении комплексные числа ничем не отличаются отобычных. ВСЯ математика - это абсолютная абстракция. Конечно исторически так сложилось, что первые изученные человечеством разделы математики способны наиболее непосредственно ОПИСЫВАТЬ объекты реального мира, но это не оправдывает грубейшую ошибку автора, противопостовляющего две абсолютные матиматические абстракции с точки зрения реальности.
>> Сам Кардано, однако, пользовался корнями из отрицательных чисел лишь как удобным практическим инструментом,
Для уточнения: действительно пользовался? Вот есть действительные корни, но детерминант отрицательный. Кардано мог получить эти корни, пользуясь своей формулой? Он же работать с комплексными числами не умел. Видимо, здесь описка.
В частных случаях получал. В общем случае нет.
Бомбелли работал уже более системно, он кубические корни из комплексных чисел вычислял. Например, тут описано https://www.ms.uky.edu/~sohum/ma330/files/eqns_4.pdf .
Большое спасибо. В общем, понятно. Кардано действовал, надо думать, либо подбором при простых коэффициентах, либо разложением на произведение многочленов меньших степеней, т.е. фактически тем же подбором. Про Бомбелли особенно интересно.
Вы своими комментариями подсказали хорошую идею, как начать вторую статью. Можно начать с разбора, а как люди вообще решали эту проблему. Собственно, Муавр первым придумал явную формулу.
А в геометрической интерпретации решение очевидно.
Как действовал Муавр.
Уже из обычных формул сложения:
следует тождество умножения:
Дальше методом математической индукции можно получить:
Именно это мы сейчас называем формулой Муавра (для целых ).
Интересно, мне почему-то ещё со школы идея о том, что i**2 =-1, казалось простой и понятной, а то, что комплексные числа связаны с вращением - надуманной абстракцией. Наверное, я в душе карданист-бомбеллист. А про вращение я никогда не мог понять, зачем связываться с комплексными числами, если у нас есть полярные координаты?
А Даламберу с Эйлером по поводу парадокса "корень из произведения" я бы сказал, что это зависит от определения. Любое число - это абстракция, тем более мнимое, и мы имеем право определить его как хотим, и можно создать две алгебры комплексных чисел: одну по Эйлеру, вторую по Даламберу. А можно провозгласить, что у нас будет два числа i (и получилось бы что-то типа кватернионов).
За статью спасибо в любом случае. Я покажу её своим детям, может быть у них это пробудит интерес к математике.
В этом и заключается геометрический подход. Вы можете любое число (любой элемент алгебраической системы) интерпретировать как преобразование некоторого пространства и изучать геометрические свойства, то есть — инварианты данных преобразований.
У полярных координат есть проблема неоднозначности: один и тот же угол поворота это и и
и ещё много углов. Комплексные числа не имеют этой проблемы.
Хорошая статья, но как же бесит открывать каждую иллюстрацию чтобы разглядеть ее. Мне кажется картинки надо адаптировать для телефонов. Для себя выработал правило: на экран телефона 20-35 строк текста. По ширине около 40 символов. Но чтобы контент не прерывался картинки лучше не делать полноэкранными. Вообще конечно на хабре сверстать статью это еще тот гемор.
Статья хорошая, есть мелкие языковые помарки, но это действительно мелочи и ерунда. Кстати, впервые узнал, что Кардано - предтеча теории вероятностей, что для меня особенно важно, поскольку веду и курс Монте Карло, и про историю рассказываю. Да даже Кардано упоминаю, но в связи с общей методой исследований и обмена результатами в то время, и как Мерсенн ее изменил! А мог бы узнать, хотя бы в Википедию заглянувши. Все лень матушка. Потому за историческую часть отдельное большое спасибо.
Но вот описание алгебраических сложностей и нарочитых формальностей для меня выглядит преувеличенным. Естественный же вопрос - как мы можем обобщить понятие числа? А вот оказывается, можем ввести упорядоченные пары чисел, определить операции так-то, и вуаля - получаем числовое поле. Если кому-то предпочтителен геометрический подход - так это дело вкуса, не более. А вот что действительно важно, так это естественная связь вот таких пар чисел с геометрией и вращениями. Как водится, исключительно по моему мнению.
А когда будут продолжены другие работы?

Царский путь к пониманию комплексных чисел. Часть I