В предыдущей статье я описал векторные языки и их ключевые отличия от обычных языков. На коротких примерах я постарался показать, как эти особенности позволяют реализовывать алгоритмы необычным образом, кратко и с высоким уровнем абстракции. В силу своей векторной природы такие языки идеально присоблены для обработки больших данных, и в качестве доказательства в этой статье я полностью реализую на векторном языке простой SQL интерпретатор. А чтобы продемонстрировать, что векторный подход можно использовать на любом языке, я реализую тот же самый интерпретатор на Rust. Преимущества векторного подхода столь велики, что даже интерпретатор в интерпретаторе сможет обработать select с группировкой из таблицы в 100 миллионов строк за 20 с небольшим секунд.
Общий план
Конечная цель - реализовать интепретатор, способный выполнять выражения типа:
select * from (select sym,size,count(*),avg(price) into r
from bt where price>10.0 and sym='fb'
group by sym,size)
as t1 join ref on t1.sym=ref.sym, t1.size = ref.sizeТ.е. он должен поддерживать основные функции типа сложения и сравнения, позволять where и group by выражения, а также - inner join по нескольким колонкам.
В качестве векторного языка я возьму Q, так как его специализация - базы данных.
Интерпретатор будет состоять из лексера, парсера и собственно интерпретатора. Для экономии места я буду приводить только ключевые места, а весь код можно найти здесь. Так же для краткости я реализую лишь часть функциональности, но так, чтобы все важное было на месте: join, where, group by, 3 типа данных, агрегирующие функции и т.п.
На примере лексера вы сможете познакомиться, пожалуй, с одним из самых красивых приемов программирования, который встречается в векторных языках, - использование данных как функций.
Парсеры оперируют деревьями и векторность тут не дает никаких преимуществ. Поэтому в этой части я сделаю упор на Rust и на то, как на нем можно реализовать генератор функциональных рекурсивно-нисходящих парсеров. Несмотря на свою второстепенность, эта часть занимает большое количество места, поэтому я перенес ее в конец, чтобы не утомлять читателей.
Наконец, сам интерпретатор. На Q он имеет весьма скромные размеры - строк 25. На Rust, конечно, гораздо больше, но написать его проще, чем может показаться. Нужно просто по шагам повторять все операции Q, адаптируя их к специфике Rust.
Это моя первая программа на Rust и сразу хочу сказать, что слухи о его сложности сильно преувеличены. Если писать в функциональном стиле (read only), то проблем нет никаких. После того, как Rust несколько раз забраковал мои идеи, я понял, чего он хочет и уже не сталкивался с необходимостью все переделывать из-за контроллера ссылок, а явные времена жизни понадобились только один раз и по делу. Зато взамен мы получаем программу, которую можно распараллелить по щелчку пальцев. Что мы и сделаем, чтобы добиться просто феноменальной производительности для столь примитивной программы.
В завершение о производительности. Векторный подход настолько крут, что без разницы - пишите вы на интерпретируемом языке или на Rust, все равно всю работу делают векторные операции. Поэтому интерпретатор на Q работает всего в полтора раза медленнее самого Q на аналогичных данных.
Лексер
Векторные языки идеальны для написания лексеров. Пусть у нас есть функция fsa, которая принимает на вход текущее состояние лексера и входной символ и возвращает новое состояние:
fsa[state;char] -> stateЕсли мы применим эту функцию последовательно ко всей входной строке, то получим на выходе последовательность состояний лексера, т.е. каждому символу будет поставлено в соответствие состояние лексера. Все, что нам остается, это найти индексы особых граничных состояний и разрезать по ним входную строку на части. Схему работы лексера можно изобразить наглядно:
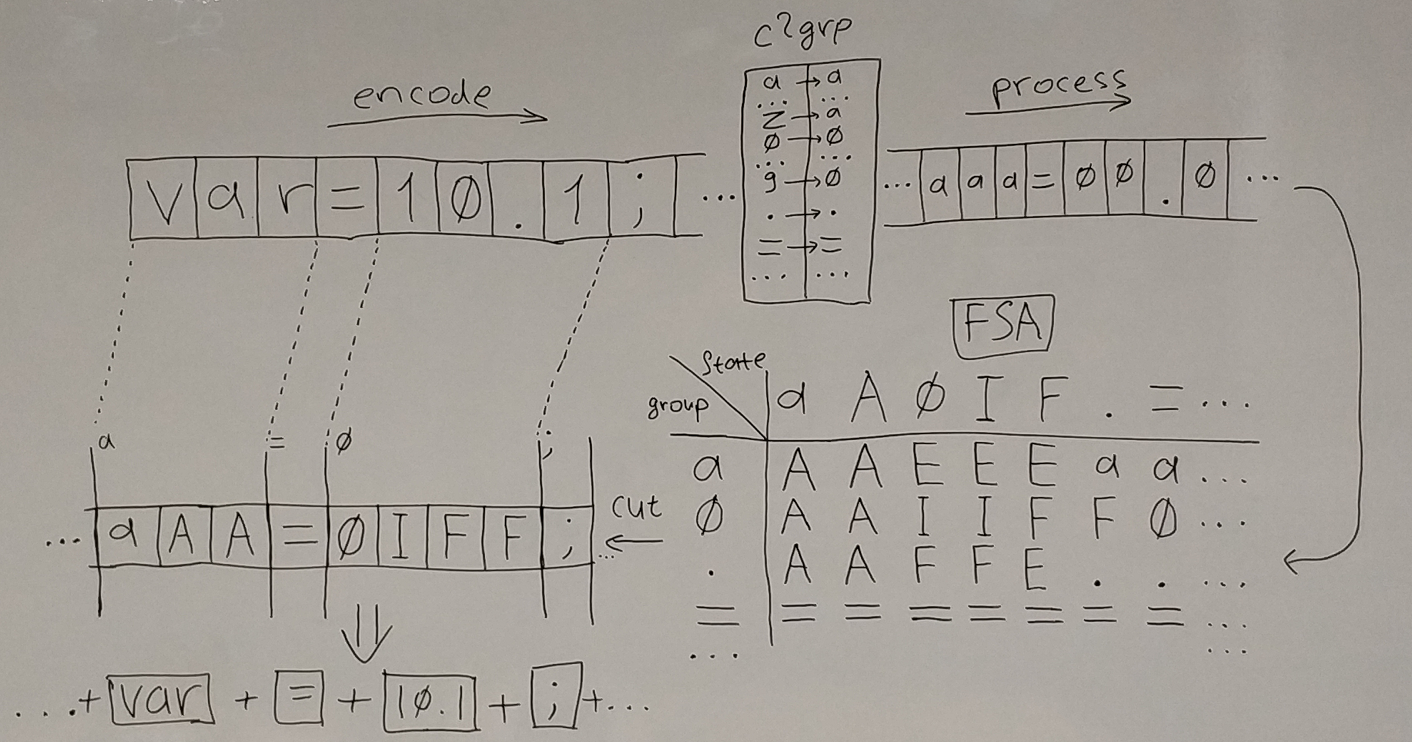
Т.е. есть следующие этапы:
Кодирование. Входные символы отображаются в группы (my.var -> aa.aaa, 12.01 -> 00.00, "str 1" -> "sss 1" и т.д.).
Трансформация. Закодированные символы пропускаются через fsa (aa.aaa -> aAAAAA, 00.00 -> 0IFFF, "sss 1" -> "SSSSSR).
Разбиваем начальную строку на части по начальным состояниям (a, 0, " и т.д.). Для удобства все не начальные состояния обозначены большими буквами.
Все три этапа - это векторные операции, поэтому на Q эта идея реализуется одной строкой (все состояния закодированы так, что начальные меньше limit):
(where fsa\[start;input]<limit)cut inputЭто в сущности весь лексер. Правда еще необходимо определить fsa. В подавляющем большинстве случаев в качестве fsa можно взять матрицу - таблицу переходов конечного автомата. Простой автомат можно задать и руками, но можно реализовать небольшой DSL. Отображение в группы можно организовать через небольшой массив (ограничимся ASCII символами для простоты):
cgrp: ("\t \r\n";"0..9";"a..zA..Z"),"\\\"=<>.'";
c2grp: 128#0; // массив [0;128]
// Q позволяет присваивать значения по индексу любой формы.
// В данном случае массиву массивов. В Rust необходимы два явных цикла:
// cgrp.iter().enumerate().for_each(|(i,&s)| s.iter()
// .for_each(|&s| c2grp[s as usize] = i + 1));
c2grp[`int$cgrp]: 1+til count cgrp;Для краткости я не привожу все цифры и буквы. Нас интересуют пробельные символы, цифры, буквы, а также несколько специальных символов. Мы закодируем эти группы числами 1, 2 и т.д., все остальные символы поместим в группу 0. Чтобы закодировать входную строку, достаточно взять индекс в массиве c2grp:
c2grp `int$stringАвтомат задается правилами (текущее состояние(я);группа(ы) символов) -> новое состояние. Для обозначения групп и начальных состояний токенов удобно использовать первые символы соответствующих групп (для группы 0..9 - 0, например). Для обозначения промежуточных состояний - большие буквы. Например, правило для имен можно записать так:
aA А a0.т.е. если автомат находится в состояниях "a" (начало имени) или "A" (внутри имени), и на вход поступают символы из групп [a,0,.], то автомат остается в состоянии "A". В начальное состояние "a" автомат попадет автоматически, когда встретит букву (это правило действует по умолчанию). После этого, если дальше он встретит букву, цифру или точку, то перейдет во внутреннее состояние "A" и будет там оставаться до тех пор, пока не встретит какой-то другой символ. Я запишу все правила без лишних комментариев (Rust):
let rules: [&[u8];21] =
[b"aA A a0.", // имена
b"0I I 0",b"0I F .",b"F F 0", // int/float
b"= E =",b"> E =",b"< E =",b"< E >", // <>, >= и т.п.
b"\" S *",b"S S *",b"\"S R \"", // "str"
b"' U *",b"U U *",b"'U V '", // 'str'
b"\tW W \t"]; // пробельные символыЧисла и строки заданы в упрощенном формате. "*" в качестве входного символа имеет специальное значение - все возможные символы. Большие буквы - это состояния внутри токенов. Такая договоренность дает нам возможность легко определить начало токена - это все состояния, которые не большие буквы.
Матрица fsa из этих правил генерируется элементарно. Схематично это выглядит так:
fsa[*;y] = y (по умолчанию для всех состояний)
"aA A a0." -> "aA","A","a0."; fsa[enc["aA"];enc["a0."]] = enc["A"]
...Необходимо закодировать символы с помощью вектора states:
states: distinct " ",(first each cgrp),raze fsa[;1];
limit: 2+count cgrp;
enc:states?; // в Q encode - это поиск индекса элемента в вектореВперед поместим все начальные состояния (пробел для учета группы 0), чтобы можно было легко определить limit.
Код генерации fsa я опускаю - он следует схеме выше.
Матрица переходов у нас есть, осталось определить саму функцию lex. В парсере нам понадобится знать тип токена, поэтому вычислим и его тоже. На Rust лексер выглядит так:
let s2n = move |v| ["ID","NUM","STR","STR","WS","OTHER"][find1(&stn,&v)];
move |s| {
if s.len()==0 {return Vec::<Token>::new()};
let mut sti = 0usize;
let st: Vec<usize> = s.as_bytes().iter().map(|b| { // st:fsa\[0;c2grp x]
sti = fsa[sti][c2grp[std::cmp::min(*b as usize,127)]];
sti}).collect();
let mut ix: Vec<usize> = st.iter().enumerate() // ix:where st<sta
.filter_map(|(i,v)| if *v<sta {Some(i)} else {None}).collect();
ix.push(st.len());
(0..ix.len()-1).into_iter()
.filter_map(|i|
match s2n(st[ix[i]]) {
"WS" => None,
kind => Some(Token{ str:&s[ix[i]..ix[i+1]], kind})
}).collect()На Q получится значительно более кратко:
s2n:(states?"a0\"'\t")!("ID";"NUM";"STR";"STR";"WS");
lex:{
i:where (st:fsa\[0;c2grp x])<limit;
{x[;where not "WS"~/: x 0]} (s2n st i;i cut x)};Если мы запустим лексер, то получим:
lex "10 + a0" -> (("NUM";"";"ID");("10";"+";"a0"))Интерпретатор
Интерпретатор можно разделить на две части - выполнение выражений и выполнение select. Первая часть тривиальна на Q, но требует большого количества кода на Rust. Я приведу основные структуры данных, чтобы было понятно, как в целом работает интерпретатор. В основе лежит enum Val:
type RVal=Arc<Val>;
enum Val {
I(i64),
D(f64),
II(Vec<i64>),
DD(Vec<f64>),
S(Arc<String>),
SS(Vec<Arc<String>>),
TBL(Dict<RVal>),
ERR(String),
}Есть три типа данных - строки, целые и нецелые, две формы их представления - атомарная и вектор. Также есть таблицы и ошибки. Dict - это пара Vec<String> и Vec<T> одинаковой длины. В случае таблицы T = Vec<RVal>, где каждый Val - это II, DD или SS. Rust позволяет в легкую распаралелливать программу, но нужно, чтобы типы данных позволяли передавать свои значения между потоками. Для этого я обернул все разделяемые значения в асинхронный счетчик ссылок Arc. Считается, что атомарные операции более медленные, однако в программе, которая работает с большими данными, это не имеет большого значения.
Интерпретатор работает с выражениями:
enum Expr {
Empty,
F1(fn (RVal) -> RRVal, Box<Expr>), // f(x)
F2(fn (RVal,RVal) -> RRVal, Box<Expr>, Box<Expr>), // f(x,y)
ELst(Vec<Expr>),
ID(String), // variable/column
Val(Val), // simple value - 10, "str"
Set(String,Box<Expr>), // 'set var expr' - assignment
Sel(Sel), // select
Tbl(Vec<String>,Vec<Expr>), // [c1 expr1, c2 expr2] - create table
}ELst и Empty используются только парсером. Expr (ссылки на себя) необходимо хранить в куче (Box). Выполняются выражения функцией eval в некотором контексте, где заданы переменные (Set), а также могут быть определены колонки таблицы:
struct ECtx {
ctx: HashMap<String,Arc<Val>>, // variables
}
struct SCtx {
tbl: Arc<Table>, // within select
idx: Option<Vec<usize>>, // idx into tbl
grp: Arc<Vec<String>>, // group by cols
}eval сравнительно проста (self = ECtx):
type RRVal=Result<Arc<Val>,String>;
fn top_eval(&mut self, e: Expr) -> RRVal {
match e {
Expr::Set(id,e) => {
let v = self.eval(*e, None)?;
self.ctx.insert(id,v.clone()); Ok(v)},
Expr::Sel(s) => self.do_sel(s),
_ => self.eval(e, None)
}
}
fn eval(&self, e: Expr, sctx:Option<&SCtx>) -> RRVal {
match e {
Expr::ID(id) => self.resolve_name(sctx,&id),
Expr::Val(v) => Ok(v.into()),
Expr::F1(f,e) => Ok(f(self.eval(*e,sctx)?)?),
Expr::F2(f,e1,e2) => Ok(f(self.eval(*e1,sctx)?,self.eval(*e2,sctx)?)?),
Expr::Tbl(n,e) => { self.eval_table(None,n,e) }
e => Err(format!("unexpected expr {:?}",e))
}
}Set и Sel нужен модифицируемый контекст, а его нельзя будет передать просто так в другой поток. Поэтому eval разбит на две части. Задача resolve_name - найти переменную или колонку и при необходимости применить where индекс. eval_table - собрать таблицу из частей и проверить, что с ней все в порядке (колонки одной длины и т.п.). Функции F1 (max, count ...) и F2 (+, >=, ...) сводятся к огромным match блокам, где для каждого типа прописывается нужная операция. Макросы позволяют уменьшить количество кода. Например, для арифметических операций часть match выглядит так:
(Val::D(i1),Val::I(i2)) => Ok(Val::D($op(*i1,*i2 as f64)).into()),
(Val::D(i1),Val::D(i2)) => Ok(Val::D($op(*i1,*i2)).into()),
(Val::I(i1),Val::II(i2)) => Ok(Val::II(i2.par_iter()
.map(|v| $op(*i1,*v)).collect()).into()),Это может показаться неоптимальным, но когда вы обрабатываете таблицу на 100 миллионов строк, это не имеет ни малейшего значения. Видите слово par_iter выше? Это все, что нужно сделать в Rust, чтобы операция стала параллельной.
Выполнение select гораздо интереснее и сложнее. Разберем его на Q, потому что код на Rust многословно повторяет код на Q, который и сам по себе непростой.
Select состоит из подвыражений (join, where, group, select, distinct, into), каждое из которых выполняется отдельно. Самое сложное из них - join. В его основе лежит функция rename, задача которой присвоить колонкам уникальные имена, чтобы не возникло конфликта при join:
// если x это name -> найти, select -> выполнить
sget:{[x] $[10=type x;get x;sel1 x]};
// в грамматике таблица определяется как '(ID|sel) ("as" ID)?'
// так что x это список из 2 элементов: (ID из as или имя таблицы;ID/select)
// y - уникальный префикс
rename:{[x;y]
t:sget x 1; // получить таблицу: names!vals
k:(k!v),(n,/:k)!v:(y,n:x[0],"."),/:k:key t; // k - оригинальные имена,
// v - уникальные, n - с префиксом (table.name)
(k;v!value t)};Все эти манипуляции сводятся к построению двух словарей - отображения из настоящих имен колонок и расширенных (table.name) в уникальные и из уникальных имен в сами колонки таблицы. Уникальные имена позволяют иметь в одной join таблице колонки с одинаковыми именами из разных таблиц и обращаться к ним в выражениях через нотацию с точкой.
В основе join следующая функция:
// x - текущая таблица в формате rename
// y - следующая таблица в этом формате
// z - join выражение, список (колонка в x;и в y)
// условие join: x[z[i;0]]==y[z[i;1]] для всех i
join_core:{[x;y;z]
// m - отображение имен в уникальные для новой таблицы x+y
// имена из x имеют приоритет
// c - переименовываем join колонки в уникальные имена
c:(m:y[0],x 0)z;
// после join z[;0] и z[;1] колонки будут одинаковыми
// поэтому колонки из y перенаправим на x
m[z[;1]]:c[;0];
// x[1]c[;0] - просто join колонки из таблицы x (подтаблица)
// y[1]c[;1] - симметрично из y
// sij[xval;yval] -> (idx1;idx2) найти индексы join в обеих таблицах
// sidx[(i1;i2);x;y без join колонок] -
// собрать новую таблицу из x и y и индексов
(m;sidx[sij[x[1]c[;0];y[1]c[;1]];x 1;c[;1]_ y 1])}
// sidx просто применяет индексы ко всем колонкам и объединяет y и z
// y z - это словари, но поскольку традиционно векторные функции имеют
// максимально широкую область определения, не нужно обращаться явно к value
sidx:{(y@\:x 0),z@\:x 1};Вся работа выполняется в функции sij, все остальное - это манипуляции именами, колонками и индексами. Если бы мы захотели добавить другой тип индекса, достаточно было бы написать еще одну sij. Конечно, функция выглядит непросто, но учитывая, что она покрывает 80% select, ей можно это простить.
Функция sij сводится к поиску строк таблицы x в таблице y. В Rust для этих целей можно использовать HashMap с быстрой hash функцией FNV - поместить в Map одну таблицу и потом искать в ней строки второй. В Q, судя по времени выполнения, скорее всего используется что-то подобное. В целом в Q у нас есть два варианта - использовать векторные примитивы или воспользоваться встроенными возможностями связанными с таблицами. В первом варианте все по-честному:
// x и y - списки колонок
sij:{j:where count[y 0]>i:$[1=count x;y[0]?x 0;flip[y]?flip x]; (j;i j)};
// или на псевдокоде
// i=find_idx[tblY;tblX]; j=i where not null i; return (j,i[j])используем функцию поиска значения в векторе (?) и транспозиции матрицы (flip). Этот вариант не такой медленный как может показаться - всего в 2.5 раза медленнее, чем оптимизированный поиск сразу по таблице (который выглядит ровно также - x?y, только x и y - таблицы, а не списки векторов). Это показывает в очередной раз силу векторных примитивов.
Наконец сам join - это просто цикл свертки по всем таблицам (fold):
// "/" это fold, rename' это map(rename)
sjoin:{[v] join_core/[rename[v 0;"@"];rename'[v 1;string til count v 1];v 2]};Остальные части select гораздо проще. where:
swhere:{[t;w] i:til count value[t 1]0; // все строки по умолчанию
$[count w;where 0<>seval[t;i;();w];i]}; // выбрать те, которые не 0
// seval такой же как eval в Rust, т.е. его сигнатура:
// seval[table,index;group by cols;expr], ECtx - это сам QОсновная функция select:
sel2:{[p] // p ~ словарь с элементами select (`j, `s, `g и т.п.)
i:swhere[tbl:sjoin p`j;p`w]; // сходу делаем join и where
if[0=count p`s; // в случае select * надо найти подходящие имена колонкам
rmap:v[vi]!key[tbl 0] vi:v?distinct v:value tbl 0;
p[`s]:{nfix[x]!x} rmap key tbl 1];
if[count p`g; // group by
// из group колонок нужен только первый элемент, нужно знать их имена
gn:nfix {$[10=type x;x;""]} each p`g;
// sgrp вернет список индексов (idx1;idx2;..) для каждой группы
// затем нужно выполнить seval[tbl;idxN;gn;exprM] для всех idx+expr
// т.е. двойной цикл, который в Q скрыт за двумя "each"
g:sgrp[tbl;i;p`g]];
:key[p`s]!flip {x[z] each y}[seval[tbl;;gn];value p`s] each g;
// если group нет, то все элементарно - просто seval для всех select выражений
(),/:seval[tbl;i;()] each p`s
};Функция sgrp в основе group by - это просто векторный примитив group, возвращающий словарь, где ключи - уникальные значения, а значения - их индексы во входном значении:
sgrp:{[t;i;g] i value group flip seval[t;i;()] each g};Я опускаю distinct и into части, поскольку они малоинтересны. В целом - это весь select на Q. В краткой записи он занимает всего 25 строк. Можно ли ждать хоть какой-то производительности от столь скромной программы? Да, потому что она написана на векторном языке!
Производительность
Напомню, что этот игрушечный интерпретатор может выполнять выражения типа
select * from (select sym,size,count(*),avg(price) into r
from bt where price>10.0 and sym='fb'
group by sym,size)
as t1 join ref on t1.sym=ref.sym, t1.size = ref.sizeи при этом справляться с таблицами в сотни миллионов строк. В частности таблица bt в выражении выше сгенерирована выражением:
// в интерпретаторе на Rust
// s = ("apple";"msft";"ibm";"bp";"gazp";"google";"fb";"abc")
// i/f - i64/f64 интервалы [0-100)
set bt [sym rand('s',100000000), size rand('i', 100000000),
price rand('f', 100000000)]Т.е. содержит 100 миллионов строк. Поначалу базовый select с group by (получается 800 групп по ~125000 элементов)
select sym,size,count(*),avg(price) into r from bt group by sym,sizeработал 44 секунды в программе на Rust, что совсем неплохо и само по себе. Однако после некоторых оптимизаций, а главное распаралелливания ключевых операций, мне удалось добиться скорости порядка 6 секунд. На мой взгляд весьма хороший результат для подобной таблицы.
Самое главное, программа на Rust, несмотря на свой внушительный вид, - это почти 1 в 1 программа на Q. Поэтому больших интеллектуальных усилий и даже отладки она не потребовала. Также благодаря векторности изначального языка ее ускорение путем распараллеливания не потребовало почти никаких усилий - если все операции изначально над массивами, то все что нужно - это вставить там и тут par_iter вместо iter.
Интерпретатор на Q не столь быстр, но вышеуказанный select всего на 50% медленнее аналогичного запроса на самом Q. Это значит, что по сути Q работает на больших данных почти также быстро, как и программа на компилируемом языке.
Хочу также отметить то, насколько великолепным языком проявил себя Rust. За все время разработки и отладки я не получил ни одного segfault и даже panic увидел всего несколько раз, и почти все это были простые ошибки выхода за пределы массива. Также поражает, насколько легко и безопасно в нем можно распараллелить задачу.
Парсер
Я отложил парсер на конец, поскольку он довольно объемен и не имеет прямого отношения к теме статьи. Тем не менее, может вам будет интересно ознакомиться с тем, как легко можно написать весьма серьезный парсер в функциональном стиле на Rust.
Это рекурсивный нисходящий парсер без заглядывания вперед. Из-за этого он не может предсказать следующий шаг и вынужден обходить все варианты. Такой парсер, конечно, медленный и не годится для серьезных задач, но для SQL выражений больше и не надо. Какая разница, парсится выражение 1 микросекунду или 10, если сам запрос займет минимум сотни микросекунд.
Такие парсеры часто пишут руками, и выглядят они примерно так:
parse_expr1(..) {
if(success(parse_expr2(..)) {
if (success(parse_str("+") || success(parse_str("-")) {
if(success(parse_expr1(..)) {
return <expr operation expr>
}
return Fail
}
return <expr>
}
return Fail;
}Главная идея предлагаемого парсера в том, что нет смысла писать это все руками, можно написать генератор подобных парсеров из BNF-подобной формы. Для всех сущностей BNF пишем по функции, затем генерируем из описания грамматики в виде строк набор парсящих функций, и все готово. В Rust, как строго типизированном языке, есть нюансы. В первую очередь определим типы для парсящих и post process функций:
type ParseFn = Box<dyn Fn(&PCtx,&[Token],usize) -> Option<(Expr,usize)>>;
type PPFn = fn(Vec<Expr>) -> Expr;ParseFn будет захватывать правила грамматики, поэтому она должна быть замыканием (closure) и лежать в куче. PCtx содержит другие ParseFn для рекурсивных вызовов и PPFn для постобработки дерева. Если парсинг не удался, она возвращает None, иначе Some с выражением и новым индексом в массив токенов. PPFn обрабатывает узел дерева, поэтому принимает безликий список выражений и превращает его в нужное выражение.
Для понимания процесса приведу часть грамматики, касающуюся выражений:
("expr", "expr1 ('or' expr {lst})? {f2}"),
("expr1","'not' expr1 {f1} | expr2 ('and' expr1 {lst})? {f2}"),
("expr2","expr3 (('='|'<>'|'<='|'>='|'>'|'<') expr2 {lst})? {f2}"),
("expr3","expr4 (('+'|'-') expr3 {lst})? {f2}"),
("expr4","vexpr (('*'|'/') expr4 {lst})? {f2}"),
("vexpr","'(' expr ')' {2} | '-' expr {f1} | call | ID | STR | NUM |
'[' (telst (',' telst)* {conc}) ']' {tblv}"),
("call", "('sum'|'avg'|'count'|'min'|'max') '(' expr ')' {call} |
'count' '(' '*' ')' {cnt} | 'rand' '(' STR ',' NUM ')' {rand}"),Тут видны ключевые части - имя правила, само правило и PP функции в фигурных скобках. Каждая продукция правила должна заканчиваться на PP функцию, поскольку правило возвращает Expr, а не Vec<Expr>. PP функция по умолчанию возвращает последний элемент вектора, поэтому кое-где PP функций нет. ID, NUM и т.п. должны обрабатываться ParseFn функцией с соответствующим именем.
Генерируется наш парсер с помощью следующей функции:
let parse = |str| {
let t = l(str); // add ({}) depth map
let mut lvl = 0;
pp_or(&t.into_iter().map(|v| {
match v.str.as_bytes()[0] {
b'(' | b'{' => lvl+=1,
b')' | b'}' => lvl-=1,
_ => ()};
(v,std::cmp::max(0,lvl))}).collect::<Vec<(Token,i32)>>()
, 0)
};l - это лексер, я переиспользую для этого лексер SQL. Нужно добавить карту глубины вложенности скобок, чтобы было удобно выделять BNF подвыражения. Поскольку это парсер для внутренних потребностей, то нет необходимости проверять правильность скобок, беспокоиться о глубине рекурсии и т.п.
Далее наше правило поступает в парсер BNF. Нужно реализовать следующие компоненты:
or правило - A | B
and правило - A B C
const правило - "(", "select".
token правило - NUM, STR.
subrule правило - expr1, call.
optional правило - A?
0+ правило - A*
1+ правило - A+
PP правило - {ppfn}
Это работа, требующая тщательности, но проделать ее нужно один раз. Например, or правило:
fn pp_or(t: &[(Token,i32)], lvl:i32) -> ParseFn {
if t.len() == 0 {return Box::new(|_,_,i| Some((Expr::Empty,i)))};
let mut r: Vec<ParseFn> = t
.split(|(v,i)| *i == lvl && v.str.as_bytes()[0] == b'|' )
.map(|v| pp_and(v,lvl)).collect();
if 1 == r.len() {
r.pop().unwrap()
} else {
Box::new(move |ctx,toks,idx|
r.iter().find_map(|f| f(ctx,toks,idx)))
}
}Функция должна вернуть ParseFn замыкание. В общем случае, когда pp_and вернула несколько ParseFn, нужно организовать цикл и выполнять подфункции, пока одна из них не вернет Some.
pp_and работает аналогично, только все ее подфункции должны вернуть Some. Также в случае успеха она должна вызвать нужную PPFn для обработки результата.
fn pp_and(t: &[(Token,i32)], lvl:i32) -> ParseFn {
if t.len() == 0 {return Box::new(|_,_,i| Some((Expr::Empty,i)))};
let (rules,usr) = pp_val(Vec::<ParseFn>::new(),t,lvl);
Box::new(move |ctx,toks,i| {
let mut j = i;
let mut v = Vec::<Expr>::with_capacity(rules.len());
for r0 in &rules {
if let Some((v0,j0)) = r0(ctx,toks,j) {
j = j0; v.push(v0)
} else {return None} };
Some((ctx.ppfns[&usr](v),j))
})
}pp_val рекурсивно обрабатывает круглые скобки и все базовые выражения. Вот некоторые примеры из нее:
// Token - if ok call rules[Token]
move |ctx,tok,i| if i<tok.len() && tok[i].kind == s
{ctx.rules[&s](ctx,tok,i)} else {None}
// Subrule
move |ctx,tok,i| ctx.rules[&s](ctx,tok,i))}
// rule?
move |ctx,tok,i| Some(rule(ctx,tok,i).unwrap_or((Expr::Empty,i)))
// rule+
move |ctx,tok,i| {
let (e,i) = plst(&rule,ctx,tok,i);
if 0<e.len() {Some((Expr::ELst(e),i))} else {None}}
// где plst
let mut j = i; let mut v:Vec<Expr> = Vec::new();
while let Some((e,i)) = rule(ctx,tok,j) {j=i; v.push(e)};
(v,j)Это весь код, необходимый для создания парсера. Чтобы его сгенерировать, нужно вызвать parse и положить правило в map:
let mut map = HashMap::new();
map.insert("expr".to_string(), parse("expr1 ('or' expr {lst})? {f2}"));
... Также необходимо определить PP функции. В большинстве случаев они сравнительно просты:
let mut pfn: HashMap<String,PPFn> = HashMap::new();
// default rule
pfn.insert("default".to_string(),|mut e| e.pop().unwrap());
// set name expr выражение
pfn.insert("set".to_string(),|mut e| Expr::Set(e.swap_remove(1).as_id(),
e.pop().unwrap().into()) );В Rust нельзя просто взять элемент из массива, поэтому необходимы функции типа swap_remove, которые делают это безопасно.
Наконец, положим правила в специальную структуру и определим для нее функцию parse:
PCtx { rules:map, ppfns:pfn}
...
impl PCtx {
fn parse(&self, t:&[Token]) -> Expr {
if let Some((e,i)) = self.rules["top"](&self,t,0) {
if i == t.len() {e}
else {Val::ERR("parse error".into()).into()}
} else {Val::ERR("parse error".into()).into()}
}
}Все, парсер готов. Он не быстр, но зато очень прост. Плюс он полностью динамический - можно менять правила во время выполнения программы, например, отключить какие-то возможности.