Разбирая старые бумаги наткнулся на изрядно потрёпанную тетрадь, в которой обнаружил наброски алгоритма поиска покрытия. Автор алгоритма Виктор Анатольевич Щербанов — мой учитель, под руководством которого я работал в девяностые годы прошлого столетия. Моё скромное участие в основном заключалось в том, что я предлагал в большинстве случаев неверные (а порой и просто бредовые) варианты. Что в общем-то не помешало Шефу (так мы его называли между собой) таки довести работу над алгоритмом до логического завершения. Где-то в двухтысячных годах алгоритм был опубликован в одном из институтских изданий Томска. Но думаю, что не лишним будет вспомнить его ещё раз. Собственно в память о Шефе я и решил написать этот пост. Может быть алгоритм покажется кому-то интересным или подтолкнёт на какие-то новые идеи по реализации алгоритма.
Сам алгоритм зиждется на двух утверждениях и двух теоремах, доказательства которых здесь не приводятся, из-за их довольно большого объёма.
Для начала определимся с тем, что мы, собственно, ищем.
Пусть задано конечное множество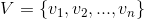 и семейство
и семейство 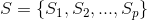 его подмножеств
его подмножеств 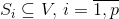 .
.
Найти подсемейство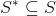 (если оно существует) такое, что
(если оно существует) такое, что 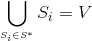 и мощность подсемейства S* (покрытия множества V) наименьшая из всех возможных.
и мощность подсемейства S* (покрытия множества V) наименьшая из всех возможных.
Следующие утверждения определяют понятия минимального и наименьшего покрытия.
Утверждение 1.
Для того чтобы подсемейство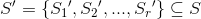 , было покрытием множества
, было покрытием множества 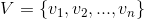 , необходимо и достаточно, чтобы выполнялось условие
, необходимо и достаточно, чтобы выполнялось условие
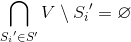
Покрытие S' называется минимальным, если не существует покрытия S'' такого, что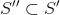 .
.
Покрытие S* называется наименьшим, если для любого минимального покрытия S' выполняется условие
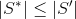
Утверждение 2.
Покрытие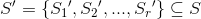 минимально тогда и только тогда, когда для любого
минимально тогда и только тогда, когда для любого 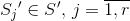 , выполняется условие
, выполняется условие
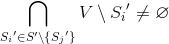
И, самое основное.
Пусть задано конечное множество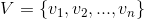 и семейство
и семейство 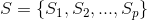 его подмножеств
его подмножеств 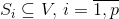 .
.
Построим полный нагруженный граф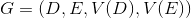 , в котором множеству
, в котором множеству 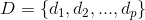 вершин графа взаимно однозначно сопоставлено семейство
вершин графа взаимно однозначно сопоставлено семейство 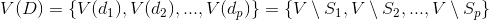 подмножеств
подмножеств  ,
,
а каждому ребру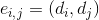 — подмножество
— подмножество 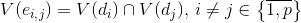 .
.
Обозначим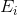 множество всех рёбер инцидентных вершине
множество всех рёбер инцидентных вершине 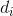 , а
, а 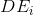 — множество всех вершин, инцидентных рёбрам из множества
— множество всех вершин, инцидентных рёбрам из множества 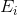 .
.
Теорема 1.
Минимальное по мощности подмножество ребер, инцидентных произвольной вершине
ребер, инцидентных произвольной вершине 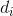 в графе G, при выполнении условий
в графе G, при выполнении условий
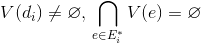
определяет минимальное покрытие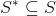 , однозначно соответствующее множеству
, однозначно соответствующее множеству 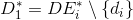 вершин, если
вершин, если 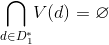 , или множеству
, или множеству 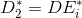 вершин, если
вершин, если 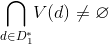 .
.
Теорема 2.
Минимальное по мощности подмножество ребер, инцидентных произвольной вершине
ребер, инцидентных произвольной вершине 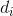 ребра
ребра 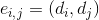 в графе G, при выполнении условий
в графе G, при выполнении условий
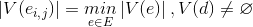 для всех
для всех 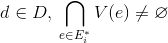
определяет наименьшее покрытие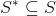 , однозначно соответствующее множеству
, однозначно соответствующее множеству 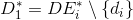 вершин, если
вершин, если 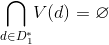 , или множеству
, или множеству 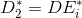 вершин, если
вершин, если 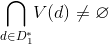 .
.
На основании теорем предлагается следующий алгоритм поиска наименьшего покрытия.
1. Множеству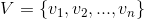 и семейству
и семейству 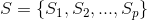 его подмножеств
его подмножеств 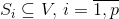 , сопоставить семейство
, сопоставить семейство 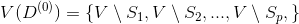 подмножеств
подмножеств 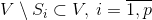 . Если для некоторого
. Если для некоторого 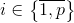 окажется
окажется 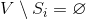 , то существует тривиальное покрытие
, то существует тривиальное покрытие 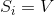 . Конец алгоритма.
. Конец алгоритма.
Иначе перейти на п.2.
2. Построить полный нагруженный граф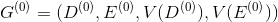 , где
, где 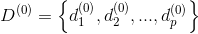 .
.
Вершину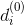 нагрузить множеством
нагрузить множеством 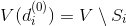
Ребро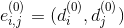 нагрузить множеством
нагрузить множеством 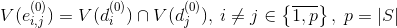 .
.
3. Проверить существование покрытия: для произвольной вершины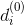 определить подмножество
определить подмножество
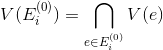 ,
,
где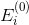 — множество рёбер, инцидентных вершине
— множество рёбер, инцидентных вершине 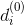 в графе
в графе 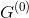 .
.
Если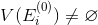 , то покрытия не существует. Конец алгоритма.
, то покрытия не существует. Конец алгоритма.
Если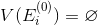 , то покрытие существует. Перейти к процедуре поиска наименьшего покрытия (п. 4).
, то покрытие существует. Перейти к процедуре поиска наименьшего покрытия (п. 4).
4. Положить t:=0.
5. В полном нагруженном графе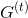 найти ребро
найти ребро 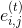 для которого выполняется условие
для которого выполняется условие 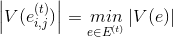 .
.
Если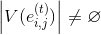 , то перейти на п. 6,
, то перейти на п. 6,
иначе — на процедуру построения множества D вершин, определяющих наименьшее покрытие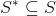 (п. 7).
(п. 7).
6. Построить полный нагруженный граф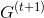 , полагая
, полагая  ,
, 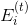 — множество рёбер, инцидентных вершине
— множество рёбер, инцидентных вершине 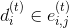 в графе
в графе 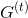 .
.
Положить для всех
для всех  .
.
Положить t:=t+1 и перейти на п. 5.
7. Начало построения множества D вершин, определяющих наименьшее покрытие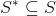 .
.
Положить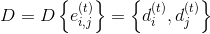 .
.
8. Если t=0, то перейти на п. 11, иначе — положить t:=t-1.
9. В графе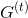 определить подмножество
определить подмножество 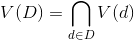
10. Если в графе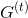 выполняется условие
выполняется условие 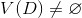 , то положить
, то положить 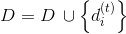 , иначе — D:=D. Перейти на п. 8.
, иначе — D:=D. Перейти на п. 8.
11. Семейство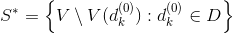 подмножеств
подмножеств 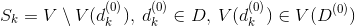 определяет наименьшее покрытие множеств
определяет наименьшее покрытие множеств 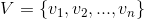 .
.
Конец алгоритма.
Попробуем оценить сложность алгоритма.
Вся, так сказать, суть алгоритма (с точки зрения оценки сложности) заключена в фразе «построим полный нагруженный граф».
Нам требуется выполнить n действий для вычисления нагрузки в n вершинах графа и (n-1)n/2 вычислений (по количеству рёбер полного графа) для нагрузки рёбер графа. И всё это, если рассматривать наихудший случай, когда подмножества взаимно не пересекаются, выполняется n-2 раза. Таким образом грубая оценка O(n) = n3 + n2.
И в заключение. Не уверен, что пост заслуживает инвайта, потому как моя причастность к алгоритму более чем сомнительная. Но опубликования, как мне кажется, стоит. Надеюсь модераторы разберутся.
Как там греки говорили? — Fais se que dois adviegne que peut (делай, что должно, и будь, что будет).
(или это были римляне?)
Сам алгоритм зиждется на двух утверждениях и двух теоремах, доказательства которых здесь не приводятся, из-за их довольно большого объёма.
Для начала определимся с тем, что мы, собственно, ищем.
Пусть задано конечное множество
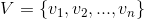 и семейство
и семейство 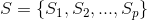 его подмножеств
его подмножеств 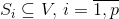 .
. Найти подсемейство
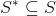 (если оно существует) такое, что
(если оно существует) такое, что 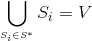 и мощность подсемейства S* (покрытия множества V) наименьшая из всех возможных.
и мощность подсемейства S* (покрытия множества V) наименьшая из всех возможных.Следующие утверждения определяют понятия минимального и наименьшего покрытия.
Утверждение 1.
Для того чтобы подсемейство
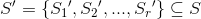 , было покрытием множества
, было покрытием множества 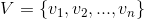 , необходимо и достаточно, чтобы выполнялось условие
, необходимо и достаточно, чтобы выполнялось условие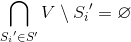
Покрытие S' называется минимальным, если не существует покрытия S'' такого, что
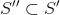 .
. Покрытие S* называется наименьшим, если для любого минимального покрытия S' выполняется условие
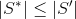
Утверждение 2.
Покрытие
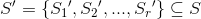 минимально тогда и только тогда, когда для любого
минимально тогда и только тогда, когда для любого 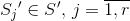 , выполняется условие
, выполняется условие 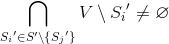
И, самое основное.
Пусть задано конечное множество
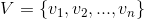 и семейство
и семейство 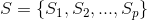 его подмножеств
его подмножеств 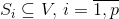 .
. Построим полный нагруженный граф
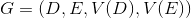 , в котором множеству
, в котором множеству 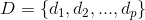 вершин графа взаимно однозначно сопоставлено семейство
вершин графа взаимно однозначно сопоставлено семейство 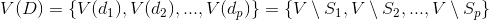 подмножеств
подмножеств  ,
, а каждому ребру
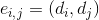 — подмножество
— подмножество 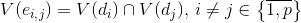 .
.Обозначим
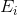 множество всех рёбер инцидентных вершине
множество всех рёбер инцидентных вершине 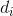 , а
, а 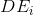 — множество всех вершин, инцидентных рёбрам из множества
— множество всех вершин, инцидентных рёбрам из множества 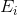 .
.Теорема 1.
Минимальное по мощности подмножество
 ребер, инцидентных произвольной вершине
ребер, инцидентных произвольной вершине 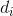 в графе G, при выполнении условий
в графе G, при выполнении условий 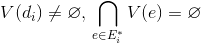
определяет минимальное покрытие
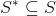 , однозначно соответствующее множеству
, однозначно соответствующее множеству 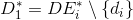 вершин, если
вершин, если 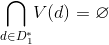 , или множеству
, или множеству 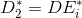 вершин, если
вершин, если 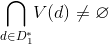 .
.Теорема 2.
Минимальное по мощности подмножество
 ребер, инцидентных произвольной вершине
ребер, инцидентных произвольной вершине 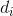 ребра
ребра 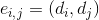 в графе G, при выполнении условий
в графе G, при выполнении условий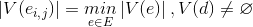 для всех
для всех 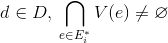
определяет наименьшее покрытие
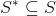 , однозначно соответствующее множеству
, однозначно соответствующее множеству 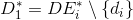 вершин, если
вершин, если 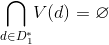 , или множеству
, или множеству 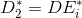 вершин, если
вершин, если 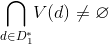 .
.На основании теорем предлагается следующий алгоритм поиска наименьшего покрытия.
1. Множеству
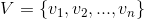 и семейству
и семейству 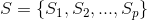 его подмножеств
его подмножеств 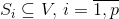 , сопоставить семейство
, сопоставить семейство 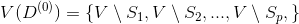 подмножеств
подмножеств 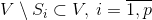 . Если для некоторого
. Если для некоторого 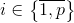 окажется
окажется 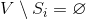 , то существует тривиальное покрытие
, то существует тривиальное покрытие 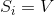 . Конец алгоритма.
. Конец алгоритма.Иначе перейти на п.2.
2. Построить полный нагруженный граф
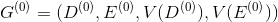 , где
, где 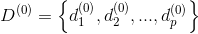 .
. Вершину
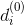 нагрузить множеством
нагрузить множеством 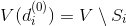
Ребро
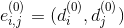 нагрузить множеством
нагрузить множеством 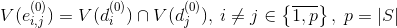 .
.3. Проверить существование покрытия: для произвольной вершины
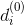 определить подмножество
определить подмножество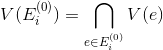 ,
, где
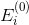 — множество рёбер, инцидентных вершине
— множество рёбер, инцидентных вершине 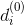 в графе
в графе 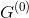 .
.Если
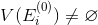 , то покрытия не существует. Конец алгоритма.
, то покрытия не существует. Конец алгоритма.Если
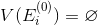 , то покрытие существует. Перейти к процедуре поиска наименьшего покрытия (п. 4).
, то покрытие существует. Перейти к процедуре поиска наименьшего покрытия (п. 4).4. Положить t:=0.
5. В полном нагруженном графе
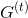 найти ребро
найти ребро 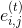 для которого выполняется условие
для которого выполняется условие 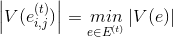 .
. Если
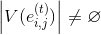 , то перейти на п. 6,
, то перейти на п. 6, иначе — на процедуру построения множества D вершин, определяющих наименьшее покрытие
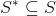 (п. 7).
(п. 7).6. Построить полный нагруженный граф
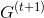 , полагая
, полагая  ,
, 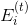 — множество рёбер, инцидентных вершине
— множество рёбер, инцидентных вершине 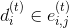 в графе
в графе 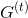 .
. Положить
 для всех
для всех  .
.Положить t:=t+1 и перейти на п. 5.
7. Начало построения множества D вершин, определяющих наименьшее покрытие
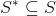 .
. Положить
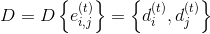 .
.8. Если t=0, то перейти на п. 11, иначе — положить t:=t-1.
9. В графе
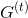 определить подмножество
определить подмножество 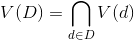
10. Если в графе
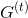 выполняется условие
выполняется условие 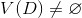 , то положить
, то положить 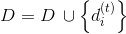 , иначе — D:=D. Перейти на п. 8.
, иначе — D:=D. Перейти на п. 8.11. Семейство
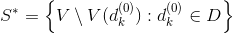 подмножеств
подмножеств 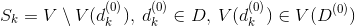 определяет наименьшее покрытие множеств
определяет наименьшее покрытие множеств 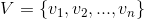 .
.Конец алгоритма.
Попробуем оценить сложность алгоритма.
Вся, так сказать, суть алгоритма (с точки зрения оценки сложности) заключена в фразе «построим полный нагруженный граф».
Нам требуется выполнить n действий для вычисления нагрузки в n вершинах графа и (n-1)n/2 вычислений (по количеству рёбер полного графа) для нагрузки рёбер графа. И всё это, если рассматривать наихудший случай, когда подмножества взаимно не пересекаются, выполняется n-2 раза. Таким образом грубая оценка O(n) = n3 + n2.
И в заключение. Не уверен, что пост заслуживает инвайта, потому как моя причастность к алгоритму более чем сомнительная. Но опубликования, как мне кажется, стоит. Надеюсь модераторы разберутся.
Как там греки говорили? — Fais se que dois adviegne que peut (делай, что должно, и будь, что будет).
(или это были римляне?)