Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Хабр доступен 24/7 благодаря поддержке друзей
Комментарии 98
А меня сокурсники до сих пор спрашивают почему я люблю математику.
Надо полагать, колода в 36 карт мало чем отличается?
Отличается. Там нужно всего полтора миллиарда лет, чтобы перебрать все варианты суперкомпьютером :)
Для колоды в 36 листов — 36! = 3.72e+41, что дает 99.999% с 25 знаками после запятой
А для колоды в 32 листа — 32! = 2.63e+35, что дает 99.999% с 19 знаками после запятой
А для колоды в 32 листа — 32! = 2.63e+35, что дает 99.999% с 19 знаками после запятой
по моему это и есть «мало чем отличается»
Ну как… В относительном выражении — отличается на много порядков. А в абсолютном — на какие-то крохи )
Вспомнилось:
Скрытый текст
Если есть отличная от нуля вероятность вероятного, то должна быть невероятной и вероятность невероятного. Ведь иначе бы сам факт вероятности вероятного стоял бы под сомнением, и вероятность вероятного подавно была бы невероятна. Значит, невероятна вероятность невероятного. Однако сколь она невероятна? Если бы вероятность невероятного была бы равна нулю, то все поле вероятности оставалось бы за вероятным, и вся вероятность всецело принадлежала бы вероятности вероятного. Почему? Т.к. любое явление либо вероятно, либо невероятно. При условии, что невероятна вероятность невероятного, любое вероятное явление становится вероятным. А если распределение вероятности идет лишь между невероятным и вероятным, то при невероятности невероятного, вероятность вероятного становится равной 100%, что невероятно, ведь тогда вероятность уже не вероятна, а определенна. Таким образом методом «от противного» доказали вероятность невероятного. Значит и вероятность вероятного уже менее вероятна? Не совсем, ведь тогда бы вероятность невероятного снова стала бы невероятной. Потому продолжим рассуждения.
С другой стороны, насколько невероятна сама невероятность? Вероятно, при малой степени вероятности невелика вероятность вероятного. И при небольшом повышении вероятности, оно становится более вероятным. Аналогично и с невероятностью. При низкой вероятности невероятности, она становится невероятно вероятной. Это куда более вероятно, нежели наличие невероятности при условии высокой вероятности самой невероятности. Отсюда и невероятность невероятности становится невероятна, из-за вероятности невероятного, за счет теории вероятности.
С другой стороны, насколько невероятна сама невероятность? Вероятно, при малой степени вероятности невелика вероятность вероятного. И при небольшом повышении вероятности, оно становится более вероятным. Аналогично и с невероятностью. При низкой вероятности невероятности, она становится невероятно вероятной. Это куда более вероятно, нежели наличие невероятности при условии высокой вероятности самой невероятности. Отсюда и невероятность невероятности становится невероятна, из-за вероятности невероятного, за счет теории вероятности.
52 карты — 80577516995772934693088976219547363208314215935442394546176000000000000 комбинаций
36 карт — 371993326789901217467999448150835200000000 комбинаций
36 карт — 371993326789901217467999448150835200000000 комбинаций
Вы забыли одну вещь: такие вероятности получаются, грубо говоря, если рассыпать все карты, а потом собрать их назад в случайном порядке. В реальности же тасовки производятся повторением простейших операций по перестановке карт местами, потому вероятности уже малость другие. А если учесть, что большинство людей тасуют карты очень нерандомными способами, вероятность попасть на расположение, которое у кого-то уже было, совсем не такая малая. Ну а если ещё вспомнить про ложные тасовки, преднамеренно или нет, но используемые рядом людей…
а в чём проблема, господа? чем вам коммент выше не по нраву?
действительно, в реальности после распаковки новой колоды и тасовки её делениями на две части и смешиванием или складыванием половинок, будет вполне ощутимая вероятность попадания в те же сочетания, особенно если крупье один. в заведениях, где новые колоды используются часто, такая коллизия из астрономически-невероятной может стать житейской.
исследование в статье сводит исследуемый процесс к сферическому в вакууме и затем моделирует его практически инструментами школьной арифметики
действительно, в реальности после распаковки новой колоды и тасовки её делениями на две части и смешиванием или складыванием половинок, будет вполне ощутимая вероятность попадания в те же сочетания, особенно если крупье один. в заведениях, где новые колоды используются часто, такая коллизия из астрономически-невероятной может стать житейской.
исследование в статье сводит исследуемый процесс к сферическому в вакууме и затем моделирует его практически инструментами школьной арифметики
Новую колоду всегда жестоко тасуют. Ибо она сортирована. А человек — не автомат. Он не может делать много раз подряд АБСОЛЮТНО такие же движения (на что даже автомат не способен).
Шулеры и крупье — еще как могут. Поищите в Ютубе видео про шулеров, увидите.
А зачем? Берём книжку карточных фокусов и там чётко описано много способов, как тасовать колоду так, чтобы в конце она была такой же, как и в начале. И вот наша теория о вероятности уникальных колод разрушилась, ибо я (как любитель этого дела) готов перемешать колоду 5 раз подряд, и каждый раз это будет одно и тоже состояние. :-)
Так-то и шахматные партии не совсем уникальны, так как на профессиональном уровне игроки стараются загнать друг друга в ловушку всем известными способами. А вот новички, которые только умеют ходить фигурами, но не умеют толком планировать стратегию — вот их игры действительно неповторимы, хотя и не так интересны :)
Сразу вспоминается Высоцкий с его «Выяснилось позже — я с испугу Разыграл классический дебют!»
Неуникальный мир потенциальных уникальностей…
Неуникальный мир потенциальных уникальностей…
Тогда уж
На третьем ходу выяснилось, что гроссмейстер играет восемнадцать испанских партий. В остальных двенадцати черные применили хотя и устаревшую, но довольно верную защиту Филидора. Если б Остап узнал, что он играет такие мудреные партии и сталкивается с такой испытанной защитой, он крайне бы удивился. Дело в том, что великий комбинатор играл в шахматы второй раз в жизни.
«Пари» (Я. И. Перельман, «Живая математика»)
— То есть какова вероятность, что первые десять прохожих все подряд окажутся мужчинами? Вычислим, как велико произведение десяти половинок. Это 1/1024, менее одной тысячной доли. Значит, если вы бьётесь о заклад, что это случится, и ставите 1 рубль, то я могу ставить 1000 рублей за то, что этого не произойдёт.
— Выгодное пари! — заявил чей-то голос. — Я бы охотно поставил рубль, чтобы получить возможность выиграть целую тысячу.
— Но имеется тысяча шансов против вашего одного, учтите и это.
— Ничего не значит. Я бы рискнул рублём против тысячи даже и за то, что сотня прохожих окажутся все подряд мужчинами.
— А вы представляете себе, как мала вероятность такого события? — спросил математик.
— Одна миллионная или что-нибудь в этом роде?
— Неизмеримо меньше! Миллионная доля получится уже для 20 прохожих. Для сотни прохожих будем иметь… Дайте-ка, я прикину на бумажке. Биллионная… Триллионная… Квадрильонная… Ого! Единица с тридцатью нулями!
— Только всего?
— Вам мало 30 нулей? В океане нет и тысячной доли такого числа мельчайших капелек.
— Внушительное число, что и говорить! Сколько же вы поставите против моего рубля?
— Ха-ха!… Все! Все, что у меня есть.
— Все — это слишком много. Ставьте на кон ваш велосипед. Ведь не поставите?
— Почему же нет? Пожалуйста! Пусть велосипед, если желаете. Я нисколько не рискую.
— И я не рискую. Не велика сумма рубль. Зато могу выиграть велосипед, а вы почти ничего.
— Да поймите же, что вы наверняка проиграете! Велосипед никогда вам не достанется, а рубль ваш можно сказать уже в моём кармане.
— Что вы делаете! — удерживал математика приятель. — Из-за рубля рискуете велосипедом. Безумие!
— Напротив, — ответил математик, — безумие ставить хотя бы один рубль при таких условиях. Верный ведь проигрыш! Уже лучше прямо выбросить рубль.
— Но один-то шанс все же имеется?
— Одна капля в целом океане. В десяти океанах! Вот ваш шанс. А за меня десять океанов против одной капельки. Мой выигрыш так же верен, как дважды два — четыре.
— Увлекаетесь, молодой человек, — раздался спокойный голос старика, все время молча слушавшего спор. — Увлекаетесь…
— Как? И вы, профессор, рассуждаете по-обывательски?
— Подумали ли вы о том, что не все случаи здесь равновозможны? Расчёт вероятности правилен лишь для каких событий? Для равновозможных, не так ли? А в рассматриваемом примере… Впрочем, — сказал старик, прислушиваясь, — сама действительность, кажется, сейчас разъяснит вам вашу ошибку. Слышна военная музыка, не правда ли?
— Причём тут музыка?.. — начал было молодой математик и осекся. На лице его выразился испуг. Он сорвался с места, бросился к окну и высунул голову.
— Так и есть! — донёсся его унылый возглас. — Проиграно пари! Прощай мой велосипед…
Через минуту всем стало ясно, в чем дело. Мимо окон проходил батальон солдат.
— Выгодное пари! — заявил чей-то голос. — Я бы охотно поставил рубль, чтобы получить возможность выиграть целую тысячу.
— Но имеется тысяча шансов против вашего одного, учтите и это.
— Ничего не значит. Я бы рискнул рублём против тысячи даже и за то, что сотня прохожих окажутся все подряд мужчинами.
— А вы представляете себе, как мала вероятность такого события? — спросил математик.
— Одна миллионная или что-нибудь в этом роде?
— Неизмеримо меньше! Миллионная доля получится уже для 20 прохожих. Для сотни прохожих будем иметь… Дайте-ка, я прикину на бумажке. Биллионная… Триллионная… Квадрильонная… Ого! Единица с тридцатью нулями!
— Только всего?
— Вам мало 30 нулей? В океане нет и тысячной доли такого числа мельчайших капелек.
— Внушительное число, что и говорить! Сколько же вы поставите против моего рубля?
— Ха-ха!… Все! Все, что у меня есть.
— Все — это слишком много. Ставьте на кон ваш велосипед. Ведь не поставите?
— Почему же нет? Пожалуйста! Пусть велосипед, если желаете. Я нисколько не рискую.
— И я не рискую. Не велика сумма рубль. Зато могу выиграть велосипед, а вы почти ничего.
— Да поймите же, что вы наверняка проиграете! Велосипед никогда вам не достанется, а рубль ваш можно сказать уже в моём кармане.
— Что вы делаете! — удерживал математика приятель. — Из-за рубля рискуете велосипедом. Безумие!
— Напротив, — ответил математик, — безумие ставить хотя бы один рубль при таких условиях. Верный ведь проигрыш! Уже лучше прямо выбросить рубль.
— Но один-то шанс все же имеется?
— Одна капля в целом океане. В десяти океанах! Вот ваш шанс. А за меня десять океанов против одной капельки. Мой выигрыш так же верен, как дважды два — четыре.
— Увлекаетесь, молодой человек, — раздался спокойный голос старика, все время молча слушавшего спор. — Увлекаетесь…
— Как? И вы, профессор, рассуждаете по-обывательски?
— Подумали ли вы о том, что не все случаи здесь равновозможны? Расчёт вероятности правилен лишь для каких событий? Для равновозможных, не так ли? А в рассматриваемом примере… Впрочем, — сказал старик, прислушиваясь, — сама действительность, кажется, сейчас разъяснит вам вашу ошибку. Слышна военная музыка, не правда ли?
— Причём тут музыка?.. — начал было молодой математик и осекся. На лице его выразился испуг. Он сорвался с места, бросился к окну и высунул голову.
— Так и есть! — донёсся его унылый возглас. — Проиграно пари! Прощай мой велосипед…
Через минуту всем стало ясно, в чем дело. Мимо окон проходил батальон солдат.
По сабжу — я в детстве любил иногда сортировать колоду карт. И думаю, я был не единственным.
И думаю, я был не единственным.Так автор посчитал 2000 лярдов перемешиваний в день на протяжении 1000 лет.
Я бы поспорил по первому условию (1 против 10). И проводил бы эксперименты возле стадионов.
Из той же книги:
Бесплатный обед
Десять молодых людей решили отпраздновать окончание средней школы товарищеским обедом в ресторане. Когда все собрались, и первое блюдо было подано, заспорили о том, как усесться вокруг стола. Одни предлагали разместиться в алфавитном порядке, другие — по возрасту, третьи — по успеваемости, четвёртые — по росту и т. д. Спор затянулся, суп успел остыть, а за стол никто не садился. Примирил всех официант, обратившийся к ним с такой речью:
— Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.
Все сели как попало. Официант продолжал:
— Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда — обещаю торжественно — я начну ежедневно угощать вас бесплатно самыми изысканными обедами.
Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами.
Однако, им не пришлось дождаться этого дня. И вовсе не потому, что официант не исполнил обещания, а потому, что число всех возможных размещений за столом чересчур велико. Оно равняется ни мало, ни много — 3 628 800. Такое число дней составляет, как нетрудно сосчитать, почти 10 000 лет!
— Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.
Все сели как попало. Официант продолжал:
— Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда — обещаю торжественно — я начну ежедневно угощать вас бесплатно самыми изысканными обедами.
Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами.
Однако, им не пришлось дождаться этого дня. И вовсе не потому, что официант не исполнил обещания, а потому, что число всех возможных размещений за столом чересчур велико. Оно равняется ни мало, ни много — 3 628 800. Такое число дней составляет, как нетрудно сосчитать, почти 10 000 лет!
Всё верно, но я как раз говорил не про заведения, а про бытовые ситуации. Большинство людей, не играющих в карты профессионально, и не являющихся крупье, не в состоянии хорошо перетасовать колоду, скорее даже наоборот. Именно про это я и писал.
Текст несколько длиннее, чем мне хотелось бы. Но выкинуть из него часть как-то не получается.
Я крайне заинтересовался этим
подразделением и решил взломать их специальный шифр.
— Разве такое возможно? — спрашивает Бишоф. — Шифрблокнот взломать
нельзя, разве что украсть копию.
— В теории верно, — говорит фон Хакльгебер. — На практике же верно,
только если буквы в шифрблокноте выбраны абсолютно случайно. Однако, как я
выяснил, это не соблюдалось для шифрблокнотов подразделения 2702, в котором
служат Уотерхауз, Тьюринг и эти два джентльмена.
— Но как вы это выяснили? — спрашивает Бишоф.
— Мне помогло несколько обстоятельств. Во первых, полнота — большое
количество сообщений. Во вторых, постоянство — все одноразовые шифрблокноты
генерировались одним способом и обнаруживали общие закономерности. Я сделал
некоторые предположения, которые впоследствии оправдались. И у меня были
счетные устройства для облегчения работы.
— Какие предположения?
— Я взял за основу гипотезу, что шифрблокноты генерирует человек,
бросая кости или тасуя колоду карт, и начал исследовать психологический
фактор. Англоязычный человек привык к определенному частотному распределению
букв. Он ожидает увидеть много е, t, s, мало z, q и x. Когда он
использует якобы случайный алгоритм выбора букв, его подсознательно
раздражают z и x, а e и t, наоборот, успокаивают. Со временем это может повлиять на
частотное распределение.
— Но, герр доктор фон Хакльгебер, мне трудно поверить, что такой
человек будет писать собственные буквы вместо тех, что вышли на картах или
игральных костях.
— Это маловероятно. Однако предположим, что алгоритм дает человеку
небольшую свободу выбора. — Фон Хакльгебер снова закуривает, подливает себе
шнапса. — Я поставил эксперимент. Пригласил двадцать добровольцев —
пожилых женщин, желавших потрудиться на благо рейха. Я посадил их составлять
одноразовые шифрблокноты по алгоритму, при котором они вытаскивали из
коробки листки бумаги. Потом я статистически обработал результаты на своем
счетном устройстве. Они вовсе не были случайными.
Роот говорит:
— Одноразовые шифрблокноты подразделения 2702 составляла миссис Тени,
жена викария. Она доставала шары с буквами из лототрона. Считалось, что она
закрывает глаза, прежде чем вытянуть шар. Однако предположим, что она даст
себе послабление и перестанет закрывать глаза.
— Или, — говорит фон Хакльгебер, — предположим, что она смотрит на
лототрон, видит, как лежат шары, и только потом закрывает глаза. Она
подсознательно тянется к E мимо Z. Или, если какая то буква только что
вышла, она постарается не взять ее снова. Даже если шаров не видно, она
научится различать их на ощупь. Шары деревянные и отличаются весом,
шероховатостью, рисунком древесных волокон.
Бишоф не готов это принять.
— Все равно они почти случайны!
— Почти — недостаточно! — отрезает фон Хакльгебер.
Да, хорошая книга.
Откуда это?
Всё равно не верю, что такой эффект помог бы взломать шифр. Может быть, специалисты по криптографии прокомментируют?
Можно я отвечу предпоследней строкой цитаты?
«Всё равно они почти случайны!»
Я не готов поручиться за то, что подобный эффект позволил кому-либо взломать шифроблокноты. Мне тоже кажется, что это невозможно. Да и привёл я фрагмент фантастической, приключенческой книги. Не стоит относиться к ней так серьёзно. А вот задуматься о самом эффекте — стоит.
«Всё равно они почти случайны!»
Я не готов поручиться за то, что подобный эффект позволил кому-либо взломать шифроблокноты. Мне тоже кажется, что это невозможно. Да и привёл я фрагмент фантастической, приключенческой книги. Не стоит относиться к ней так серьёзно. А вот задуматься о самом эффекте — стоит.
А что, собственно, в этой книге фантастического (за исключением присутствия библейского персонажа — личность которого, впрочем, в рамках книги не раскрывается)?
Ну, предположим, что в шифроблокноте нет ни одной буквы Z (или какая там соответствует нулю) — а остальные равновероятны. Получим, что в зашифрованной записке каждая буква будет не той, что была в исходной, а заменена на случайную другую букву. И чем это может помочь?
Да, один символ там несёт примерно 0.06 бита информации. Так что в некоторых ситуациях, например, когда у документа есть «шапка» длиной в 100 символов, имеющая только 50 возможных (известных) вариантов, то шансы определить правильный вариант достаточно высоки. Но текст в шифровках, всё-таки, уплотняется, чтобы уменьшить избыточность — это сделает взлом ещё сложнее.
Есть другой вопрос. Допустим, что шифроблокнот состоит из осмысленного текста на известном языке. Передаётся тоже осмысленный неуплотнённый текст. Другой дополнительной информации нет, сообщение только одно. Действительно ли можно сумму двух текстов «распутать» и получить оба текста?
Есть другой вопрос. Допустим, что шифроблокнот состоит из осмысленного текста на известном языке. Передаётся тоже осмысленный неуплотнённый текст. Другой дополнительной информации нет, сообщение только одно. Действительно ли можно сумму двух текстов «распутать» и получить оба текста?
«случайный срез и перестановка» — это всего лишь циклическая перестановка. Она даст только 52 варианта, сколько раз её ни применяй. Для достижения любого варианта надо, в простейшем случае, иметь возможность делить колоду на три части и переставлять две из них. Причём лучше бы менять номера частей, которые переставляются. Такие операции можно выполнить даже одной рукой (у меня наилучший результат — нетривиальная перестановка пяти частей).
Если типичный шаг тасовки — разделить колоду на две части, а потом «врезать» одну в другую, т.е. смешать их с сохранением порядка каждой части, то число исходов такого шага равно 2^52-2. За пять шагов получим число исходов, большее, чем 52!. Конечно, многие из этих исходов совпадут, да и исходы одного шага не равновероятны (колоду стараются делить на примерно равные части), но количество возможных комбинаций будет сопоставимо с 52!..
Вопрос: какое минимальное число операций «разделить и врезать» нужно, чтобы получить обратный порядок карт?
Вопрос: какое минимальное число операций «разделить и врезать» нужно, чтобы получить обратный порядок карт?
Да, так. Другой вопрос: определить по заданной перестановке минимальное число шагов, достаточное для её получения.
У меня есть гипотеза, но доказать её пока не получается.
У меня есть гипотеза, но доказать её пока не получается.
Алгоритм как раз очень прост — обычная сортировка слиянием. Сгруппируем карты в блоки (исходно каждый блок будет содержать по одной карте). На каждом шаге будем делить колоду так, чтобы в обоих частях оказалось одинаковое число блоков — и в процессе «врезки» выполним слияние блоков, оказавшихся напротив друг друга.
Это был алгоритм решения исходной задачи. Если же требуется получить не обратный порядок карт, а произвольный — то надо в начале делать блоки не по одной карте, а сколько влезет, но чтобы внутри одного блока они шли в правильном порядке. Мне трудно доказать, что число блоков получится как раз
PS но как вы так красиво оценили минимальное число ходов? Уж поделитесь, пожалуйста… 3 часа думал, не придумалось ничего.
Это был алгоритм решения исходной задачи. Если же требуется получить не обратный порядок карт, а произвольный — то надо в начале делать блоки не по одной карте, а сколько влезет, но чтобы внутри одного блока они шли в правильном порядке. Мне трудно доказать, что число блоков получится как раз
m+1 — но интуитивно так и получается :)PS но как вы так красиво оценили минимальное число ходов? Уж поделитесь, пожалуйста… 3 часа думал, не придумалось ничего.
Да, мой ответ оказался совсем неправильным (это был логарифм максимальной длины убывающей подпоследовательности). А про число инверсий — надо подумать. Для начала — как распутать последовательность 2,1,4,3,6,5,...,14,13 (7 инверсий, т.е. должно хватить трёх ходов).
Разбиваем на блоки:
Первый ход (разбиваем колоду между 8 и 7, с каждой стороны по 4 блока):
Второй ход (разбиваем колоду между 12 и 3, с каждой стороны по 2 блока):
Третий ход — разбиваем колоду между 14 и 1, с каждой стороны по блоку, после их слияния колода упорядочена.
2 | 1 4 | 3 6 | 5 8 | 7 10 | 9 12 | 11 14 | 13Первый ход (разбиваем колоду между 8 и 7, с каждой стороны по 4 блока):
2 7 10 | 1 4 9 12 | 3 6 11 14 | 5 8 13Второй ход (разбиваем колоду между 12 и 3, с каждой стороны по 2 блока):
2 3 6 7 10 11 14 | 1 4 5 8 9 12 13Третий ход — разбиваем колоду между 14 и 1, с каждой стороны по блоку, после их слияния колода упорядочена.
Стоит разделить 52! на 4! — ведь в большинстве игр масти вполне взаимозаменяемы. Для оценки сверху следует пренебречь играми, чувствительными к мастям, таким как преферанс (тем более, что я не знаю преферанса на 52 листа).
Вы ведь понимаете, что поделив 8*10^(67) на 24 — мало что изменится?
Вопрос на самом деле интересный, хотя и пример с заменяемыми мастями неудачный. В бридже, например, 52 карты раздаются четверым игрокам по 13 штук. Порядок, в котором игрок получил карты, не имеет абсолютно никакого значения. Некоторые игроки, получив свои 13 карт, сперва перетасовывают их не глядя, а потом уже смотрят. Поэтому реальных вариантов 52!/(13!^4) = 5.3*10^28, что на 40 порядков меньше числа, озвученного автором.
Возможно я старый сноб, но этот факт был рассказан нам в институте на первой или второй лекции по теории вероятности.
А теперь посчитайте вероятность того, что среднестатистический пользователь Хабра ходил в ваш институт на лекции по теории вероятности.
мой институт совершенно ни чем не выделяется на фоне остальных по стране. Как не выделяется и то, что основы теории вероятности считаются обязательным образовательным минимумом даже для тех кто к математике имеет очень опосредованное отношение.
Примерно как три закона Ньютона. Достаточно знать, что они есть и уже будешь выглядеть не таким безграмотным.
Примерно как три закона Ньютона. Достаточно знать, что они есть и уже будешь выглядеть не таким безграмотным.
на первых двух лекциях по теории я пил пиво во дворе дома рядом с универом, вроде как, так что вероятность стала меньше.
А в чём смысл статьи так и осталось непонятным. Для чего нам нужно знать, уникальна ли колода после тасования или нет? Ведь исход игры зависит не только от комбинации и положения карт в колоде, но и от действий игроков, в случае, если разрабатывается стратегия.
Как мне кажется, вся вышеперечисленная выкладка из разряда бесполезных фактов.
Как мне кажется, вся вышеперечисленная выкладка из разряда бесполезных фактов.
Да, довольно неожиданно даже для человека, знакомого с теорией вероятностей.Сфига бы? Я хоть и сдал тервер на 3, но полученный в статье результат даже для меня был более чем ожидаем.
Один я вспомнил «Девять миллиардов имен Бога»?
Чем то напоминает GUID.
«Помни! Каждый раз когда ты перемешиваешь колоду карт, ты, скорее всего, крадешь у вселенной одну уникальную комбинацию...»
«Помни! Каждый раз когда ты перемешиваешь колоду карт, ты, скорее всего, крадешь у вселенной одну уникальную комбинацию...»
Хм, вот кто-то еще открыл учебник теории вероятностей…
www.youtube.com/watch?v=wBXRduZThZQ интересно узнать вероятность таких машин
Вероятность уникальной колоды крайне мала. Но какова вероятность того, что среди 73*10^16 было хотя две одинаковых? У меня громоздкие цифры получаются. Задача перекликается с Парадоксом дней рождения
При чем тут парадокс дней рождения? Нам надо выяснить не существование совпадающих колод вообще, а уникальность конкретной колоды. Когда один из элементов пары фиксирован, парадокс дней рождения не возникает.
Я предлагаю вторую задачу. Посчитать вероятность одинаковых раскладов за гипотетическую историю или подсчитать сколько надо сделать шафлов, чтобы с вероятностью 0,5 получить две одинаковые.
В колоде ещё есть два джокера.
Ф. Мостеллер «Пятьдесят занимательных вероятностных задач с решениями», второе издание (М.: Наука, главная редакция физико-математической литературы, 1975)
Решая задачу, автор книги получает вероятность «1 к 160 биллионам», и тут же задаётся вопросом:
и сам же выдвигает предположение об основных причинах:
В статье приведён расчёт для модели хорошего перемешивания удобной колоды. Результат занимателен и показателен (в духе зёрен на клетках шахматной доски). Но всегда надо помнить об области применимости модели.
Задача 8
Часто приходится слышать, что некто при игре в бридж получил на руки 13 пик. Какова вероятность, при условии, что карты хорошо перетасованы, получить 13 карт одной масти? (Каждый из четырех игроков в бридж получает 13 карт из колоды в 52 карты.)
Решая задачу, автор книги получает вероятность «1 к 160 биллионам», и тут же задаётся вопросом:
Чем можно объяснить значительную бОльшую частоту сообщений о появлении «масти»?
и сам же выдвигает предположение об основных причинах:
- склеивание карт;
- плохое тасование;
- шутки и мистификации.
В статье приведён расчёт для модели хорошего перемешивания удобной колоды. Результат занимателен и показателен (в духе зёрен на клетках шахматной доски). Но всегда надо помнить об области применимости модели.
В сущности, все модели неправильны, но некоторые полезны(Джордж Бокс)
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
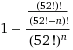
Вероятность намешать уникальную колоду карт. Неожиданный результат