То, о чем я попытаюсь сейчас рассказать, выглядит как настоящая магия.
Если вы что-то знали о нейронных сетях до этого — забудьте это и не вспоминайте, как страшный сон.
Если вы не знали ничего — вам же легче, полпути уже пройдено.
Если вы на «ты» с байесовской статистикой, читали вот эту и вот эту статьи из Deepmind — не обращайте внимания на предыдущие две строчкии разрешите потом записаться к вам на консультацию по одному богословскому вопросу.
Итак, магия:

Слева — обычная и всем знакомая нейронная сеть, у которой каждая связь между парой нейронов задана каким-то числом (весом). Справа — нейронная сеть, веса которой представлены не числами, а демоническими облаками вероятности, колеблющимися всякий раз, когда дьявол играет в кости со вселенной. Именно ее мы в итоге и хотим получить. И если вы, как и я, озадаченно трясете головой и спрашиваете «а нафига все это нужно» — добро пожаловать под кат.
Давайте для начала путешествия возьмем самую простую в мире нейронную сеть, состоящую аж из одного нейрона. Отпилим у него функцию активации и заставим выплевывать просто произведение входов на веса (w) плюс b, и получим то, что называется линейной регрессией.
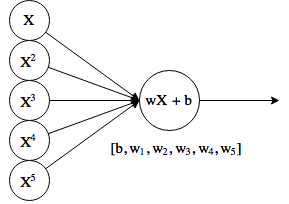
На входе дополнительно есть несколько копий оригинального X, возведенных в степень. Это иногда еще называют полиномиальной регрессией, хотя теоретически, «нейрон» по-прежнему делает линейную функцию
Ну и как в классических задачках, допустим, у нас есть какие-то точки, и нам нужно подогнать под них функцию. Напишем какой-то такой не очень красивый, зато самый простой в мире код:
И получим примерно такое:

Функция, которую мы пытаемся пропихуть через синие точки, прямо сейчас задана полиномом пятой степени, а коэффициенты у нее такие: . Допустим, мы посмотрели на график, убедились, что зеленая линия не делает ничего особенно плохого и удачно подходит под данные, может быть, проверили, как она ведет себя на отдельной (предварительно спрятаной) тестовой выборке, и нас все устроило. Тогда эти шесть цифр — найденная нами почти-истина, какие-то «настоящие» параметры, управляющие законами природы (в данном случае законом функции
. Допустим, мы посмотрели на график, убедились, что зеленая линия не делает ничего особенно плохого и удачно подходит под данные, может быть, проверили, как она ведет себя на отдельной (предварительно спрятаной) тестовой выборке, и нас все устроило. Тогда эти шесть цифр — найденная нами почти-истина, какие-то «настоящие» параметры, управляющие законами природы (в данном случае законом функции  , но это детали — давайте предположим, что мы смотрим на какие-то настоящие и очень важные данные, что-нибудь типа графика температур для оценки глобального потепления).
, но это детали — давайте предположим, что мы смотрим на какие-то настоящие и очень важные данные, что-нибудь типа графика температур для оценки глобального потепления).
Окей, если мы нашли настоящие параметры, почему зеленая линия все-таки неидеально проходит через синие точки? Среднеквадратичное отклонение для этой линии все еще не нулевое (на самом деле оно примерно 0.97). Это нормально, или мы что-то сделали не так? На этот вопрос есть два ответа:
1. Наша модель недостаточно крута и недостаточно полно отражает искомую закономерность. Мы можем «обогатить» ее, добавив еще параметров — т.е., увеличить степень полинома. Для точек нам достаточно взять полином степени
точек нам достаточно взять полином степени  , чтобы он идеально прошел через все точки.
, чтобы он идеально прошел через все точки.

… не совсем идеально, но а почему бы и нет. Выглядит даже немного симпатичней, по-моему. Оставим как рабочую гипотезу.
2. Наша модель достаточно крута, проблема — в данных. В них есть какой-то шум, вызванный не иначе как несовершенством нашего мира (в данном случае тем, что я предательски приплюсовал к точкам немного рандома, но давайте представим себе, что это какие-то реальные данные). Даже если этот шум не по-настоящему случайный, а правда вызван факторами, которые мы не учли при постановке задачи, мы можем моделировать его как случайный — и считать, что колебания, вызванные вариациями всех этих факторов, может быть, удачненько лягут в нормальное распределение.
Не знаю, как вам, а мне второй вывод кажется если даже и не сразу правильным, то как минимум первоочередным. В конце концов, мы всегда можем подозревать, что в наших данных будет какой-то шум, мешающий планам и отклоняющий точки от нужного значения. Подумаем сначала про него, а дальше, если что, можно и степень полинома подкрутить.
Итак, мы делаем второй вывод, произносим слово «шум» и немедленно переносимся в теорию вероятностей. Удобнее всего (во всяком случае, мне) представить это так: наша зеленая линия пытается «прострелить» все синие точки, которые играют роль мишеней, при этом она может «промахиваться мимо», и размер промаха — как раз и есть тот самый шум. Предположим, что он Гауссовый (почему бы и нет). Тогда выстрел по мишени будет выглядеть так:
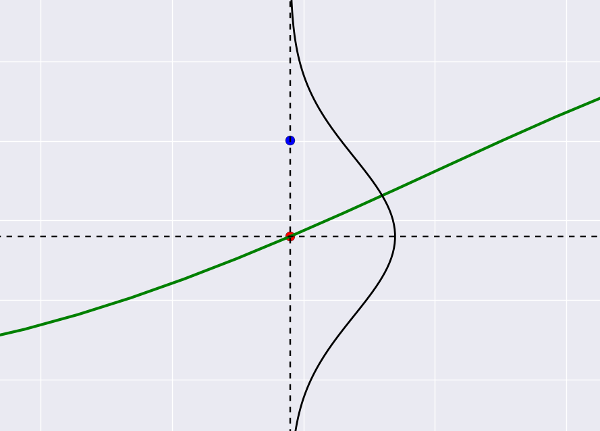
Это все тот же график регрессии, только с зумом. Синяя точка — фактическое значение из датасета, красная — то, что предсказывает регрессия. Маленькие отклонения синего от красного вероятней (лежат недалеко от центра гауссианы), большие — менее вероятны. Становится понятно, что если мы предскажем «неправильный центр» (разместим красную точку где-то далеко), отклонение для синей точки станет большим и следовательно, маловероятным.
В переводе на чуть более общепринятый язык эту вероятность называют правдоподобием (likelihood) и записывают в нашем гауссовском случае как (где
(где  и
и  — центр и стандартное отклонение гауссовой кривой), а в общем случае как
— центр и стандартное отклонение гауссовой кривой), а в общем случае как  , где под
, где под  имеют в виду любые параметры. Смысл у нее везде одинаковый — «вероятность того, что если распределением данных управляют такие-то параметры
имеют в виду любые параметры. Смысл у нее везде одинаковый — «вероятность того, что если распределением данных управляют такие-то параметры  , результат будет именно
, результат будет именно  ».
».
Теперь мы можем слегка переформулировать задачу регрессии. В терминах мишеней и правдоподобия они будет звучать как-то так: стрелять так, чтобы стрелок не выглядел полным неудачником, то есть чтобы его промахи были похожи на промахи и лежали в рамках погрешности. Придерживаясь общепринятого статистического языка, нам нужно максимизировать правдоподобие.
Сама искомая вероятность, как мы предположили, задается нормальным распределением. Спишем из википедии формулу и перемножим вероятности для каждой точки между собой (отсюда индекс ):
):

Ооокей, выглядит уже немного пугающе. Давайте, чтобы было немного полегче, зафиксируем — тогда мы сможем выкинуть половину символов отсюда. Чтобы у нас не портилось выражение вероятности, отдельно укажем, что нас интересует максимум:
— тогда мы сможем выкинуть половину символов отсюда. Чтобы у нас не портилось выражение вероятности, отдельно укажем, что нас интересует максимум:

Хээй, стало значительно веселее. Возьмем от этой штуки логарифм. Точка максимума при этом никуда не денется, зато произведение превратится в сумму, а экспонента — в свой показатель:

Ну и совсем наконец, уберем минус в сумме, заменив максимум на минимум:

Хм, где-то я уже видел такое выражение…
… и оказывается, что максимум правдоподобия достигается там же, где и минимум среднеквадратического отклонения регрессии. Такие моменты всегда почему-то ужасно разочаровывают — я уже был уверен, что щас открою какой-нибудь новый метод регрессии, а мы вернулись туда, откуда начинали.
С другой стороны, теперь мы знаем ответ на вопрос «а почему мы используем именно среднеквадратическое отклонение?» Раньше мы на это мысленно разводили руками, а теперь в курсе, что оно соответствует гауссовому шуму. Бонус-материал — если для оптимизации регрессии использовать абсолютную ошибку ( ), то получится шум по Лапласу (такой заостренный в центре). От вопроса «а чем один лучше другого» стыдливо уклонимся.
), то получится шум по Лапласу (такой заостренный в центре). От вопроса «а чем один лучше другого» стыдливо уклонимся.
Ладно, все это было весело, и довольно общеизвестно, на самом деле — мы тут просто на досуге переизобрели метод максимального правдоподобия. Настало время шагнуть чуть глубже и на другой уровень сна.
… как вы думаете, есть ли у вселенной параметры?
Это серьезный вопрос. Мы еще из школьной физики знаем, что у некоторых вещей вроде как точно есть — ускорение свободного падения, скажем, равно 9.8 метра на секунду в квадрате, и если мы хотим узнать, как падают вещи, или скажем, замоделировать компьютерную игру с физикой, нам придется это число туда вкрутить (или как делают компьютерные игры, хм? может, там притяжение Земли делается по закону Ньютона? или, черт возьми, с учетом эффектов теории относительности?). Или скажем, у пространства есть три измерения (макроскопических измерения, поправляет меня Мартин Риз); не 3.1 и не 2.8, а точно 3. Если бы мы вдруг решили построить алгоритм машинного обучения, который бы решил измерить размерность пространства, мы бы тем выше оценивали его работу, чем ближе бы он казался к числу три.
С другой стороны, есть ли точный, фиксированный параметр у того, сколько молока ребенок должен выпить за месяц? Сколько песен должна спеть птица, чтобы найти себе пару? В какой пропорции уменьшится опухоль после инъекции вещества X в тело пациента? Сколько воды протекает сквозь ручей за три минуты времени? Все эти вещи, несомненно, имеют под собой определенную закономерность — опухоль будет уменьшаться, ребенок — пить молоко, вода — течь, но если мы будем замерять точные значения, они постоянно будут колебаться, оставаясь при этом в каком-то интервале. Там, где в случае с физикой использование более точных инструментов дает нам все более точное значение величины («секунда есть время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133»), для измерения раковой опухоли нам скорее понадобится больше подопытных больных, чтобы очертить верхнюю и нижнюю границу и быть готовым к разным вариантам развития событий.
Это вообще вопрос откуда-то скорее из философии — и где-то здесь проходит водораздел между байесовской и ортодоксальной (или частотной) статистикой. Если грубо (я чуть дальше исправлюсь), то ортодоксальный подход скажет, что на каком-то уровне настоящие параметры все-таки есть (просто мы еще до него не добрались, а когда-нибудь выяснится, что рост опухоли, скажем, зависит от комбинации нескольких четко определяемых факторов). Байесовец же скажет, что точного параметра не существует — если даже не на уровне физического дизайна вселенной, то на уровне наблюдаемых нами эффектов — и что с параметрами надо обращаться как со случайными величинами, которые могут колебаться в разные стороны.
Давайте применим байесовскую философию «параметры — это случайные величины» к коэффициентам нашей регрессии. Для этого спишем теорему Байеса:
%20%3D%20%5Cfrac%7BP(X%20%5Cmid%20%5Ctheta)P(%5Ctheta)%7D%7BP(X)%7D)
Здесь означает «параметры в общем виде»; в нашем случае это уже знакомые коэффициенты полинома
означает «параметры в общем виде»; в нашем случае это уже знакомые коэффициенты полинома  . И мы уже знаем как минимум одну фигню из этой формулы —
. И мы уже знаем как минимум одну фигню из этой формулы — ) , то самое правдоподобие, которое мы максимизировали секцией выше (еще раз вспомним, что оно считается как значение отклонений точек датасета от регрессионной кривой или как «средний размер промаха по мишени»).
, то самое правдоподобие, которое мы максимизировали секцией выше (еще раз вспомним, что оно считается как значение отклонений точек датасета от регрессионной кривой или как «средний размер промаха по мишени»).  называется априорной (prior) вероятностью и отражает наше изначальное предположение о том, как выглядит распределение параметров.
называется априорной (prior) вероятностью и отражает наше изначальное предположение о том, как выглядит распределение параметров.  в отечественной литературе, по-моему, никак специально не называется (полная вероятность?), в других версия ее можно встретить под словом evidence — это общая вероятность получить такие данные, как у нас есть, при всех возможных значениях параметров
в отечественной литературе, по-моему, никак специально не называется (полная вероятность?), в других версия ее можно встретить под словом evidence — это общая вероятность получить такие данные, как у нас есть, при всех возможных значениях параметров  (пока не очень понятно, откуда ее брать). И наконец,
(пока не очень понятно, откуда ее брать). И наконец,  — апостериорная вероятность (posterior), которая означает буквально «что мы думаем о распределении параметров после того, как увидели данные».
— апостериорная вероятность (posterior), которая означает буквально «что мы думаем о распределении параметров после того, как увидели данные».
… на самом деле есть даже-не-очень-сложные способы выразить posterior для регрессии аналитически — т.е., получить формулу, куда только подставить значения из датасета, и получится правильный ответ. Но мы будем делать все раздолбайским программистским способом — численно, итеративно, и совершенно неэффективно. Зато не придется читать про всякие инвертированные распределения Уишарта и прочие жуткие вещи, которые не проходят в школе (хотя потом все равно придется, так что если вы за хардкорный путь познания, то вэлкам). Логика тут такая:
— мы начинаем с состояния полного незнания, когда у нас есть только prior. То есть мы считаем, что коэффициенты у регрессии могут быть какие угодно. Чтобы ограничить бездну познания немного, скажем «какие угодно от -10 до 10».
— мы видим какой-то кусок данных (одну точку из датасета, скажем). Для каждой возможной комбинации параметров мы считаем правдоподобие — насколько вероятно, что выстрел по мишени делался именно с такими настройками. Как можно заранее догадаться, большинство настроек будут скорее невалидными, и выстрел унесет куда-то совсем мимо, но явно останется несколько (больше одного) вариантов, при которых дырка в мишени выглядит разумно. Правдоподобие мы считаем, как уже видели, по Гауссу — просто подставляем в формулу плотности нормального распределения предсказание регрессии вместо мю, а значение из датасеты — вместо икс.
мы считаем правдоподобие — насколько вероятно, что выстрел по мишени делался именно с такими настройками. Как можно заранее догадаться, большинство настроек будут скорее невалидными, и выстрел унесет куда-то совсем мимо, но явно останется несколько (больше одного) вариантов, при которых дырка в мишени выглядит разумно. Правдоподобие мы считаем, как уже видели, по Гауссу — просто подставляем в формулу плотности нормального распределения предсказание регрессии вместо мю, а значение из датасеты — вместо икс.
— суммируем все рассчитанные на предыдущем шаге значения правдоподобия и получаем (в чем легко убедиться, написав
(в чем легко убедиться, написав  ). Теперь у нас есть все необходимое, чтобы проапдейтить posterior.
). Теперь у нас есть все необходимое, чтобы проапдейтить posterior.
— обработав одну мишень, мы получили какие-то представления о том, как могут выглядеть параметры; теперь это становится нашим новым prior. Достаем следующую точку из датасета и начинаем со второго шага.
Выглядит это все довольно несложно:
(перебрать все возможных комбинации коэффициентов нам поможет
В результате мы получим совместное распределение для наших коэффициентов регрессии — все их возможные значения будут суммироваться к единице. Получается, что у каждого набора коэффициентов будет какая-то вероятность, причем чем выше она, тем задаваемая ими кривая правильней и трушней.
Возникает вопрос на миллион — как эту фигню нарисовать?
Я попробовал примерно так: разбил спектр вероятностей на десять равных отрезков, и из каждого отрезка нарисовал на графике сколько-то кривых соответствующим цветом (от черного к белому — чем выше вероятность кривой). «Низковероятных» кривых, очевидно, больше, чем высоковероятных, поэтому пришлось ограничить их число рандомной сотней или около того, чтобы pyplot окончательно не умер в мучениях, пытаясь нарисовать… сколько, кстати, кривых? Я временно понизил степень полинома до третьей, каждый коэффициент может принимать значения от -10 до 10 с шагом в 0.5 — так что скромных регрессий там, где раньше была одна.
регрессий там, где раньше была одна.
Итого, выглядит это примерно так:
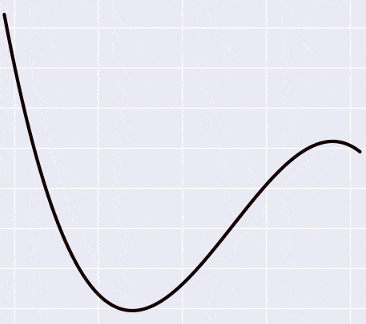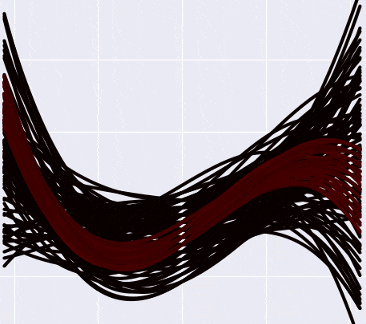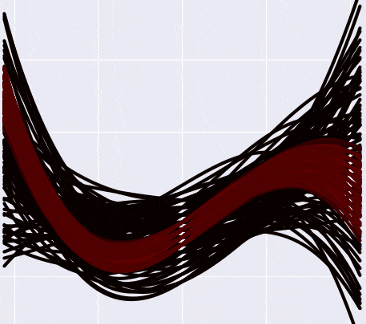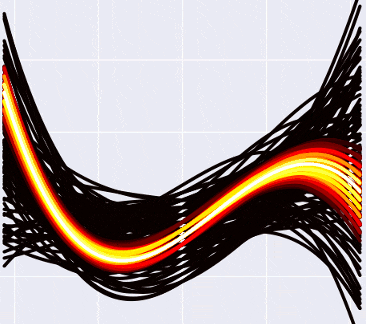
А если отметить на графике данные, то так (прошу прощения за вырвиглазно-зеленый цвет):
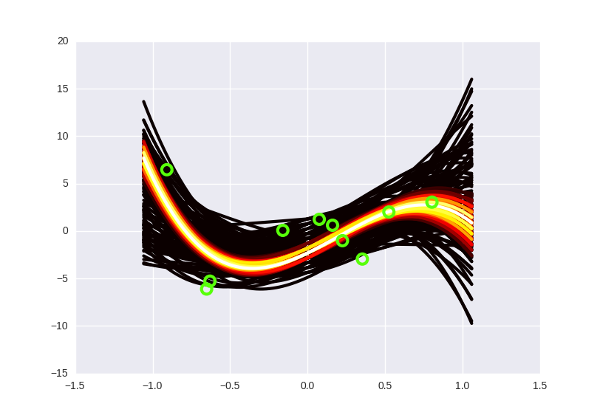
Заметьте, что более «горячие» кривые, конечно, имеют более высокую вероятность, но в Байесовской интерпретации это не означает, что эти кривые «правильные» (что мы должны взять их и выбросить все черные). Немного более интуитивный способ думать об этих кривых, по-моему — это представить, что вы смотрите как бы сверху на нормальное распределение, и видите, что в центре, конечно, есть какой-то пик вероятности, но сама по себе вероятность оказаться в точке пика все равно очень маленькая. Только собрав вместе какую-то часть распределения, можно «набрать» достаточно вероятности.
Если вы все еще недоумеваете, зачем нам эта штука, то вот вам маленький бонус: байесовская регрессия неуязвима к переобучению (overfitting). Причем я не имею в виду просто «устойчива» или «надежна» как регрессия с регуляризацией — в определенной степени она к нему вообще неуязвима.
Что такое переобучение, еще раз? Это когда мы «слишком подгоняем» модель к имеющимся данным (например, подбираем такую кривую, которая идеально пройдет через все точки датасета, но покажет плохие предсказания на новых данных). В переводе на философский язык прошлой секции это означает, что когда мы искали «правильный» набор параметров, мы нашли какой-то ошибочный, неправильный. Это невозможно сделать с байесовским подходом, потому что там просто нет понятия «правильного» набора параметров! Странный черно-желтый конус на картинках выше говорит нам: «да, скорее всего, следующие точки будут где-то в середине вдоль белых кривых, но могут оказаться и с краю, и выше, и ниже, никаких проблем». Степень полинома можно увеличивать сколько угодно: вместе с ней будет расти число возможных кривых, а у каждой из них по отдельности будет падать вероятность. «Выживут» все равно только те, которые будут лежать близко к данным, в нашем оранжево-«горячем» пучке. Сделаем пятую степень? Да никаких проблем, Хьюстон:

Выглядит чуть более блеклым, но это просто потому, что я уменьшил общее количество кривых — иначе мой лаптоп бы не проснулся.
На самом деле в таком контексте понятия переобучения вообще не существует. Невозможно неправильно найти параметр, потому что «параметр» — это не вещь, которую можно «найти», это здоровенное облако вероятности, которое становится «плотным» только там, где рядом лежат данные. Переобучения не существует, дамы и господа, расходимся. Не забудем сообщить всем этим важным ребятам из машинного обучения, что можно закрывать лавочку.
В машинном обучении есть такая очень простая техника — когда у вас есть несколько моделей и они все работают плохо, можно взять и усреднить (или еще как-нибудь объединить) их предсказания, и тогда они волшебным образом начинают работать хорошо. По-правильному это называется ансамбли, и их можно встретить почти где угодно, особенно на соревнованиях.
И вообще говоря, это не интуитивный вопрос: почему ансамбли вообще работают? В реальной жизни вещи редко ведут себя таким образом: если у вас есть десять плохих молотков, гвоздь не станет забиваться лучше от того, что вы будете использовать их по очереди. Иллюстрация к этому вопросу частично служит неплохой интуицией (по-моему) на тему того, почему работает байесовская регрессия. Выглядит это как-то так:
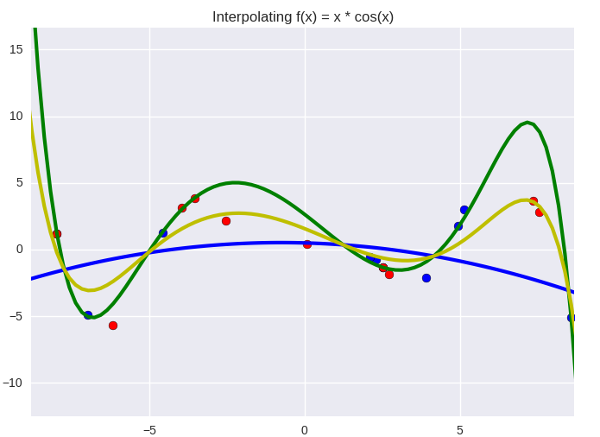
Зеленая линия — «сложная» модель (полином девятой степени), а синяя — «простая» (второй степени). Синией точки относятся к обучающей выборке, а красные — к тестовой. Желтая линия — простое среднее арифметическое между двумя моделями, и даже на глаз заметно, что она не такая размашистая, как зеленая, и действительно лежит ближе к красным точкам. Простота синего слегка компенсирует прыгучесть зеленого; средний вариант ближе к истине, чем оба отклонения, при условии, что отклонения направлены в разные стороны (это как раз одно из важных условий ансамблей — вам нужны разные модели для того, чтобы усреднение сработало).
Так вот, когда мы пытаемся предсказать что-то с байесовской регрессией, мы усредняем не две и не три модели, а — в нашем случае — два с половиной миллиона. Но погодите, на самом деле все еще круче. Это мы в своем кривом питонском коде ограничили коэффициенты значениями в -10 и 10 с шагом в 0.5, а если делать все по-правильному, они могут принимать любое значение на бесконечной числовой прямой. Секунду, включим калькулятор… , так точно. Байесовская регрессия — это ансамбль из бесконечного числа регрессий (сумма при этом превращается в интеграл). Где-то в этот момент скромное название «байесовская регрессия» начинает не передавать всей ее невозможной крутости, нужно бы что-нибудь эпичнее.
, так точно. Байесовская регрессия — это ансамбль из бесконечного числа регрессий (сумма при этом превращается в интеграл). Где-то в этот момент скромное название «байесовская регрессия» начинает не передавать всей ее невозможной крутости, нужно бы что-нибудь эпичнее.
«Не-совсем-случайный бесконечнолес?»
Настало время немного разочароваться: способ, который мы придумали для расчета posterior, плохой и работает только для каких-то очень маленьких задач. Дело в том, что количество всех возможных сочетаний параметров, которые нужно перебрать, растет экспоненциально. Мы оценивали его как число значений параметра в степени числа параметров, и уже для полинома девятой степени (десять коэффициентов/параметров) нам в текущем сеттинге придется пробежаться по циклу 10485760000000000 раз.
А теперь настало время по-настоящему разочароваться: для более сложных моделей, то есть нейронных сетей (которые представляют собой просто несколько регрессионных юнитов, соединенных друг с другом), чистый байесовский метод становится еще более неприменимым. «Параметры» нейронной сети — это ее веса; а их в современных сетях может быть очень и очень много (миллионы штук с легкостью). Существуют всякие способы упростить этот процесс: например, случайным образом доставать значения posterior вместо того, чтобы рассчитывать его в каждой точки (это называется сэмплинг), но мы не зря их все проигнорировали — они недостаточно круты, чтобы помочь получить байесовскую нейронную сеть по-настоящему серьезных размеров.
На самом деле для каких-то отдельных моделей все еще хуже. Наши коэффициенты регрессии, грубо говоря, «ни от чего не зависели»; если мы хотим посмотреть, как ведет себя модель с таким-то набором параметров, мы можем просто взять его и подставить в формулу Байеса. В сетях распределение весов отдельного нейрона может зависеть от того, как ведет себя предыдущий нейрон, а тот, в свою очередь, зависит от предыдущего (а настоящее веселье начинается, когда зависимости замыкаются в цикл).
Собственно, это и есть главная причина, по которой лавочка не закрыта, люди продолжают бороться с переобучениеми искусственный интеллект так и не построили. В общем, если мы хотим добраться до цели, указанной в заголовке, нам потребуется что-нибудь еще. Поэтому в следующей части мы поговорим об аппроксимациях к апостерорной вероятности, вариационных методах в машинном обучении, и об обратном байесораспространении ошибки.
Мы можем немного отступить назад и удовлетвориться частичным решением проблемы: найти максимум байесовского пучка, самую близкую к центру и самую «горячую» кривую. Это будет не так круто, как знание пучка целиком, но все лучше, чем то, с чего мы начинали.
То есть мы ищем . Берем привычный логарифм, чтобы превратить произведение в сумму:
. Берем привычный логарифм, чтобы превратить произведение в сумму:

Теперь смотрите: с мы уже разобразись в части про максимальное правдоподобие (под спойлером), и можем его пока проигнорировать. Что делать со вторым слагаемым (которое наш prior)? Для начала, вспомним, что
мы уже разобразись в части про максимальное правдоподобие (под спойлером), и можем его пока проигнорировать. Что делать со вторым слагаемым (которое наш prior)? Для начала, вспомним, что  в нашем случае — это набор коэффициентов регрессии, и в качестве априорной оценки мы вполне можем сказать, что каждый коэффициент имеет какое-то свое, независимое распределение (т.е., записать выражение как
в нашем случае — это набор коэффициентов регрессии, и в качестве априорной оценки мы вполне можем сказать, что каждый коэффициент имеет какое-то свое, независимое распределение (т.е., записать выражение как  ). Какое именно распределение взять? Мы раньше считали, что оно равномерное:
). Какое именно распределение взять? Мы раньше считали, что оно равномерное:  , но это скучно и сводится к максимальному правдоподобию (потому что тогда
, но это скучно и сводится к максимальному правдоподобию (потому что тогда  будет константой — вероятность все время одинаковая, какие бы коэффициенты мы не взяли). Давайте предположим, что каждый коэффициент регрессии распределен по Гауссу с центром в точке 0 и каким-то стандартным отклонением
будет константой — вероятность все время одинаковая, какие бы коэффициенты мы не взяли). Давайте предположим, что каждый коэффициент регрессии распределен по Гауссу с центром в точке 0 и каким-то стандартным отклонением  . Тогда:
. Тогда:

Подставляем вместо формулу нормального распределения. Мы уже такое делали, только если помните, раньше у нас было фиксировано стандартное отклонение, а середина варьировалась. Сейчас мы фиксируем сразу все:
формулу нормального распределения. Мы уже такое делали, только если помните, раньше у нас было фиксировано стандартное отклонение, а середина варьировалась. Сейчас мы фиксируем сразу все:

Коэффициент перед экспонентой опять-таки не важен для поиска максимума (он не зависит от ). Выкидываем его и применяем логарифм:
). Выкидываем его и применяем логарифм:

Получается, что максимум достигается там, где сумма квадратов коэффициентов регрессии минимальна. Ничего не напоминает? Мы переизобрели регуляризацию, на минуточку, и получили отличное обоснование тому, зачем она вообще нужна (раньше это была какая-то технарско-инженерная штука, в духе «нуу, давайте просто заставим коэффициенты регрессии быть маленькими, чтобы она не прыгала туда-сюда», но с Байесом в ваш дом приходит просветление и все обретает смысл).
На статистическом жаргоне это называется maximum a posteriori или MAP-learning. В отличие от «чистого» Байеса, MAP отлично применяется и к нейронным сетям, и к чему угодно — под скромным именем «регуляризация». К сожалению, это не тру-байесовское решение, потому что в конце концов мы заканчиваем игру с каким-то штучным «набором параметров» — и поэтому такой подход тоже может страдать от переобучения, хотя и более устойчив к нему, чем метод максимального правдоподобия.
По мотивам дискуссии, начатой haqreu на тему того, православно ли пытаться объяснять математические вещи на пальцах, мне немного интересно общественное мнение на эту тему. Ткните куда-нибудь в опрос по результатам прочтения, если не затруднит?
Если вы что-то знали о нейронных сетях до этого — забудьте это и не вспоминайте, как страшный сон.
Если вы не знали ничего — вам же легче, полпути уже пройдено.
Если вы на «ты» с байесовской статистикой, читали вот эту и вот эту статьи из Deepmind — не обращайте внимания на предыдущие две строчки
Итак, магия:
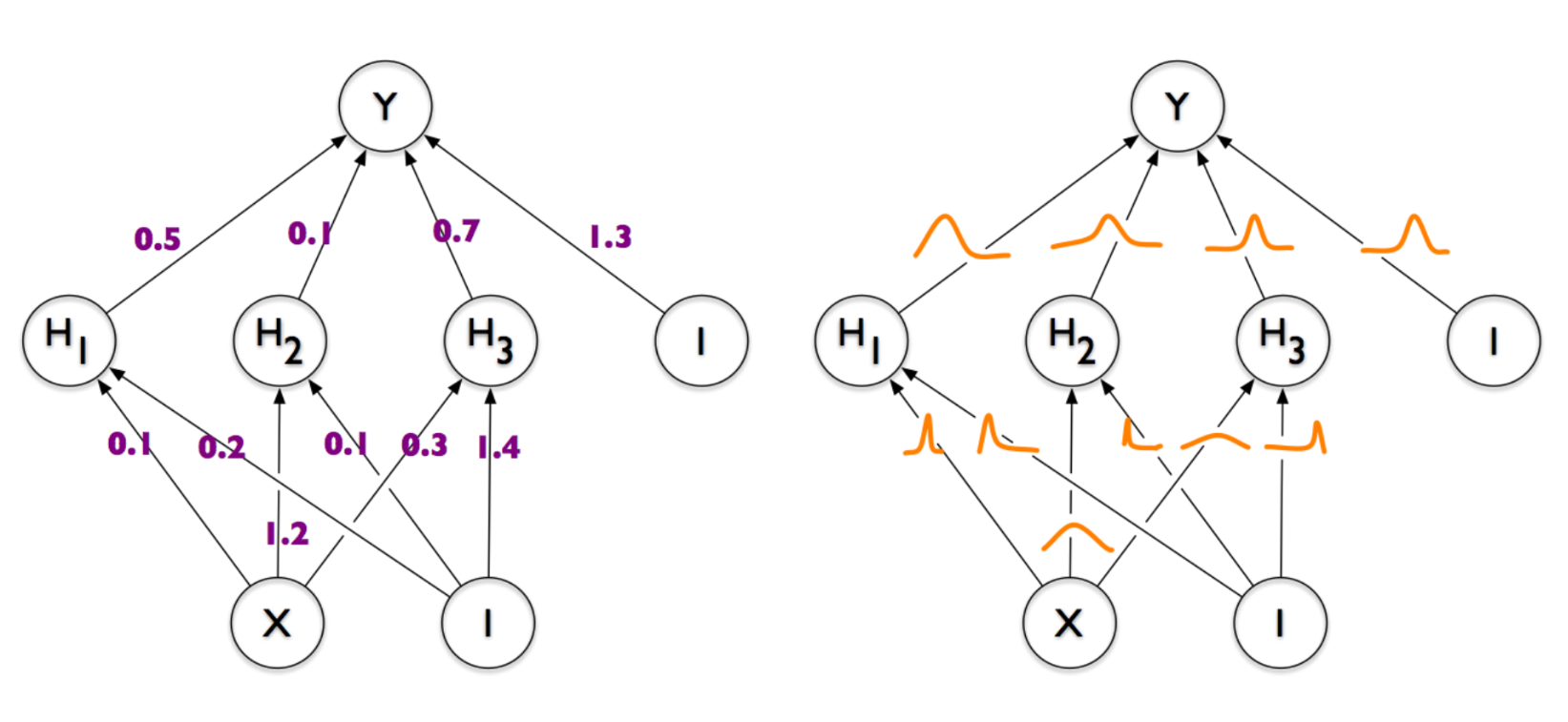
Слева — обычная и всем знакомая нейронная сеть, у которой каждая связь между парой нейронов задана каким-то числом (весом). Справа — нейронная сеть, веса которой представлены не числами, а демоническими облаками вероятности, колеблющимися всякий раз, когда дьявол играет в кости со вселенной. Именно ее мы в итоге и хотим получить. И если вы, как и я, озадаченно трясете головой и спрашиваете «а нафига все это нужно» — добро пожаловать под кат.
Один шаг назад: линейная регрессия
Давайте для начала путешествия возьмем самую простую в мире нейронную сеть, состоящую аж из одного нейрона. Отпилим у него функцию активации и заставим выплевывать просто произведение входов на веса (w) плюс b, и получим то, что называется линейной регрессией.
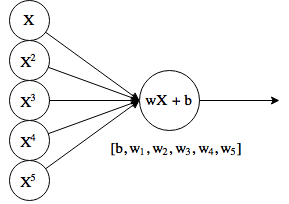
На входе дополнительно есть несколько копий оригинального X, возведенных в степень. Это иногда еще называют полиномиальной регрессией, хотя теоретически, «нейрон» по-прежнему делает линейную функцию
Ну и как в классических задачках, допустим, у нас есть какие-то точки, и нам нужно подогнать под них функцию. Напишем какой-то такой не очень красивый, зато самый простой в мире код:
Заголовок спойлера
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
def add_powers(data, n=5):
result = [data]
for i in xrange(2, n + 1):
poly = np.power(data, i)
result.append(poly)
return np.vstack(result).T
def generate_data(n=20):
x = np.linspace(-10, 10, 100)
y = x * np.cos(x)
max_y = np.max(y)
y += np.random.random(y.shape)
idx = np.random.choice(len(y), n)
return x[idx], y[idx], max_y
if __name__ == '__main__':
original_data, target, max_y = generate_data(n=10)
power = 5
data = add_powers(original_data, power)
max_vals = np.array([max_y ** i for i in xrange(1, power + 1)])
data /= max_vals
w = (np.random.random(power) - 0.5) * 1.
b = -1.
learning_rate = 0.1
for e in xrange(100000):
h = data.dot(w) + b
w -= learning_rate * ((h - target)[:, None] * data).mean(axis=0)
b -= learning_rate * (h - target).mean()
plt.title('Interpolating f(x) = x * cos(x)')
x = add_powers(np.linspace(-10, 10, 100), power)
x /= max_vals
y = x.dot(w) + b
plt.plot(x[:, 0] * max_vals[0], y, lw=3, c='g')
plt.scatter(data[:, 0] * max_vals[0], target, s=50)
plt.show()
И получим примерно такое:
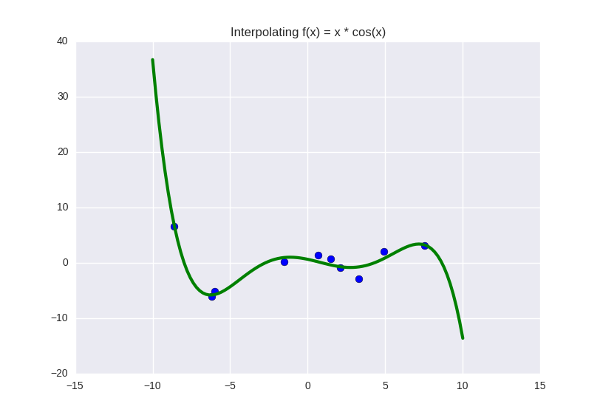
Функция, которую мы пытаемся пропихуть через синие точки, прямо сейчас задана полиномом пятой степени, а коэффициенты у нее такие:
[0.5423 -3.2648 -16.5311 43.3645 25.6159 -51.2418]. Что это, на всякий случай, означает? Это означает, что мы подозреваем в данных какую-то закономерность, и эта закономерность лучше всего выражается как Вероятностная интерпретация
Окей, если мы нашли настоящие параметры, почему зеленая линия все-таки неидеально проходит через синие точки? Среднеквадратичное отклонение для этой линии все еще не нулевое (на самом деле оно примерно 0.97). Это нормально, или мы что-то сделали не так? На этот вопрос есть два ответа:
1. Наша модель недостаточно крута и недостаточно полно отражает искомую закономерность. Мы можем «обогатить» ее, добавив еще параметров — т.е., увеличить степень полинома. Для
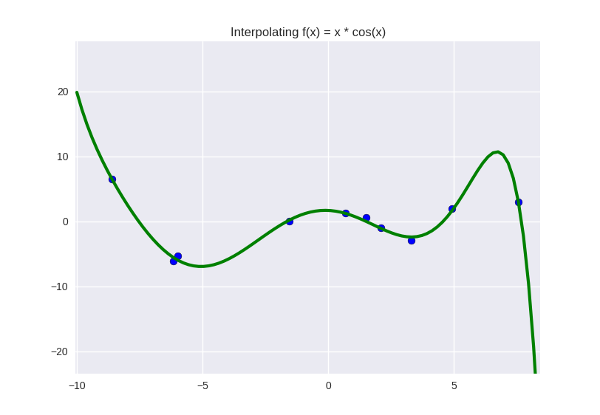
… не совсем идеально, но а почему бы и нет. Выглядит даже немного симпатичней, по-моему. Оставим как рабочую гипотезу.
2. Наша модель достаточно крута, проблема — в данных. В них есть какой-то шум, вызванный не иначе как несовершенством нашего мира (в данном случае тем, что я предательски приплюсовал к точкам немного рандома, но давайте представим себе, что это какие-то реальные данные). Даже если этот шум не по-настоящему случайный, а правда вызван факторами, которые мы не учли при постановке задачи, мы можем моделировать его как случайный — и считать, что колебания, вызванные вариациями всех этих факторов, может быть, удачненько лягут в нормальное распределение.
Не знаю, как вам, а мне второй вывод кажется если даже и не сразу правильным, то как минимум первоочередным. В конце концов, мы всегда можем подозревать, что в наших данных будет какой-то шум, мешающий планам и отклоняющий точки от нужного значения. Подумаем сначала про него, а дальше, если что, можно и степень полинома подкрутить.
Итак, мы делаем второй вывод, произносим слово «шум» и немедленно переносимся в теорию вероятностей. Удобнее всего (во всяком случае, мне) представить это так: наша зеленая линия пытается «прострелить» все синие точки, которые играют роль мишеней, при этом она может «промахиваться мимо», и размер промаха — как раз и есть тот самый шум. Предположим, что он Гауссовый (почему бы и нет). Тогда выстрел по мишени будет выглядеть так:
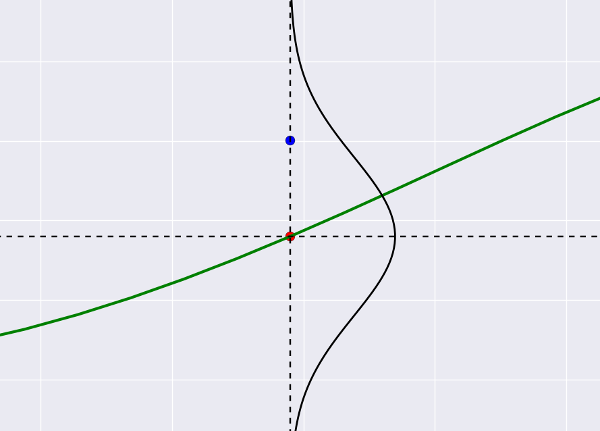
Это все тот же график регрессии, только с зумом. Синяя точка — фактическое значение из датасета, красная — то, что предсказывает регрессия. Маленькие отклонения синего от красного вероятней (лежат недалеко от центра гауссианы), большие — менее вероятны. Становится понятно, что если мы предскажем «неправильный центр» (разместим красную точку где-то далеко), отклонение для синей точки станет большим и следовательно, маловероятным.
В переводе на чуть более общепринятый язык эту вероятность называют правдоподобием (likelihood) и записывают в нашем гауссовском случае как
Теперь мы можем слегка переформулировать задачу регрессии. В терминах мишеней и правдоподобия они будет звучать как-то так: стрелять так, чтобы стрелок не выглядел полным неудачником, то есть чтобы его промахи были похожи на промахи и лежали в рамках погрешности. Придерживаясь общепринятого статистического языка, нам нужно максимизировать правдоподобие.
Сама искомая вероятность, как мы предположили, задается нормальным распределением. Спишем из википедии формулу и перемножим вероятности для каждой точки между собой (отсюда индекс
Ооокей, выглядит уже немного пугающе. Давайте, чтобы было немного полегче, зафиксируем
Хээй, стало значительно веселее. Возьмем от этой штуки логарифм. Точка максимума при этом никуда не денется, зато произведение превратится в сумму, а экспонента — в свой показатель:
Ну и совсем наконец, уберем минус в сумме, заменив максимум на минимум:
Хм, где-то я уже видел такое выражение…
… и оказывается, что максимум правдоподобия достигается там же, где и минимум среднеквадратического отклонения регрессии. Такие моменты всегда почему-то ужасно разочаровывают — я уже был уверен, что щас открою какой-нибудь новый метод регрессии, а мы вернулись туда, откуда начинали.
С другой стороны, теперь мы знаем ответ на вопрос «а почему мы используем именно среднеквадратическое отклонение?» Раньше мы на это мысленно разводили руками, а теперь в курсе, что оно соответствует гауссовому шуму. Бонус-материал — если для оптимизации регрессии использовать абсолютную ошибку (
Think Bayes
Ладно, все это было весело, и довольно общеизвестно, на самом деле — мы тут просто на досуге переизобрели метод максимального правдоподобия. Настало время шагнуть чуть глубже и на другой уровень сна.
… как вы думаете, есть ли у вселенной параметры?
Это серьезный вопрос. Мы еще из школьной физики знаем, что у некоторых вещей вроде как точно есть — ускорение свободного падения, скажем, равно 9.8 метра на секунду в квадрате, и если мы хотим узнать, как падают вещи, или скажем, замоделировать компьютерную игру с физикой, нам придется это число туда вкрутить (или как делают компьютерные игры, хм? может, там притяжение Земли делается по закону Ньютона? или, черт возьми, с учетом эффектов теории относительности?). Или скажем, у пространства есть три измерения (макроскопических измерения, поправляет меня Мартин Риз); не 3.1 и не 2.8, а точно 3. Если бы мы вдруг решили построить алгоритм машинного обучения, который бы решил измерить размерность пространства, мы бы тем выше оценивали его работу, чем ближе бы он казался к числу три.
С другой стороны, есть ли точный, фиксированный параметр у того, сколько молока ребенок должен выпить за месяц? Сколько песен должна спеть птица, чтобы найти себе пару? В какой пропорции уменьшится опухоль после инъекции вещества X в тело пациента? Сколько воды протекает сквозь ручей за три минуты времени? Все эти вещи, несомненно, имеют под собой определенную закономерность — опухоль будет уменьшаться, ребенок — пить молоко, вода — течь, но если мы будем замерять точные значения, они постоянно будут колебаться, оставаясь при этом в каком-то интервале. Там, где в случае с физикой использование более точных инструментов дает нам все более точное значение величины («секунда есть время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133»), для измерения раковой опухоли нам скорее понадобится больше подопытных больных, чтобы очертить верхнюю и нижнюю границу и быть готовым к разным вариантам развития событий.
Это вообще вопрос откуда-то скорее из философии — и где-то здесь проходит водораздел между байесовской и ортодоксальной (или частотной) статистикой. Если грубо (я чуть дальше исправлюсь), то ортодоксальный подход скажет, что на каком-то уровне настоящие параметры все-таки есть (просто мы еще до него не добрались, а когда-нибудь выяснится, что рост опухоли, скажем, зависит от комбинации нескольких четко определяемых факторов). Байесовец же скажет, что точного параметра не существует — если даже не на уровне физического дизайна вселенной, то на уровне наблюдаемых нами эффектов — и что с параметрами надо обращаться как со случайными величинами, которые могут колебаться в разные стороны.
На самом деле...
Обе стороны могут сейчас сказать, что я неправ, потому что интерпретаций этого вопроса — целая куча. Интересующихся отсылаю на StackExchange, откуда я позаимствовал несколько примеров вроде молока и опухоли, и более правильный ответ для байесовской статистики скорее будет «мы не знаем, как там устроен мир на самом деле, и возможно, фиксированные параметры и есть, но в своих взаимодействиях с ними мы неизменно оперируем с некоторым градусом неуверенности, и эту неуверенность мы моделируем с помощью вероятности». Фух. Срочно нужен выход на более мелкий уровень сна.
2560000 регрессий
Давайте применим байесовскую философию «параметры — это случайные величины» к коэффициентам нашей регрессии. Для этого спишем теорему Байеса:
Здесь
… на самом деле есть даже-не-очень-сложные способы выразить posterior для регрессии аналитически — т.е., получить формулу, куда только подставить значения из датасета, и получится правильный ответ. Но мы будем делать все раздолбайским программистским способом — численно, итеративно, и совершенно неэффективно. Зато не придется читать про всякие инвертированные распределения Уишарта и прочие жуткие вещи, которые не проходят в школе (хотя потом все равно придется, так что если вы за хардкорный путь познания, то вэлкам). Логика тут такая:
— мы начинаем с состояния полного незнания, когда у нас есть только prior. То есть мы считаем, что коэффициенты у регрессии могут быть какие угодно. Чтобы ограничить бездну познания немного, скажем «какие угодно от -10 до 10».
— мы видим какой-то кусок данных (одну точку из датасета, скажем). Для каждой возможной комбинации параметров
— суммируем все рассчитанные на предыдущем шаге значения правдоподобия и получаем
— обработав одну мишень, мы получили какие-то представления о том, как могут выглядеть параметры; теперь это становится нашим новым prior. Достаем следующую точку из датасета и начинаем со второго шага.
Выглядит это все довольно несложно:
Заголовок спойлера
from itertools import product
def likelihood(x, mu, sigma=1.):
return np.exp(-np.power(x - mu, 2.) / (2 * np.power(sigma, 2.)))
frequency = 40
posterior = np.ones(frequency ** (power + 1)) / float(frequency)
param_values = [np.linspace(-10, 10, frequency) for _ in xrange(power + 1)]
for i, pt in enumerate(data):
for j, params in enumerate(product(*param_values)):
b = params[0]
w = np.array(params[1:])
h = pt.dot(w) + b
like = likelihood(pt[0], h)
posterior[j] *= like
posterior /= posterior.sum()
(перебрать все возможных комбинации коэффициентов нам поможет
itertools.product)В результате мы получим совместное распределение для наших коэффициентов регрессии — все их возможные значения будут суммироваться к единице. Получается, что у каждого набора коэффициентов будет какая-то вероятность, причем чем выше она, тем задаваемая ими кривая правильней и трушней.
Возникает вопрос на миллион — как эту фигню нарисовать?
Я попробовал примерно так: разбил спектр вероятностей на десять равных отрезков, и из каждого отрезка нарисовал на графике сколько-то кривых соответствующим цветом (от черного к белому — чем выше вероятность кривой). «Низковероятных» кривых, очевидно, больше, чем высоковероятных, поэтому пришлось ограничить их число рандомной сотней или около того, чтобы pyplot окончательно не умер в мучениях, пытаясь нарисовать… сколько, кстати, кривых? Я временно понизил степень полинома до третьей, каждый коэффициент может принимать значения от -10 до 10 с шагом в 0.5 — так что скромных
Итого, выглядит это примерно так:

А если отметить на графике данные, то так (прошу прощения за вырвиглазно-зеленый цвет):
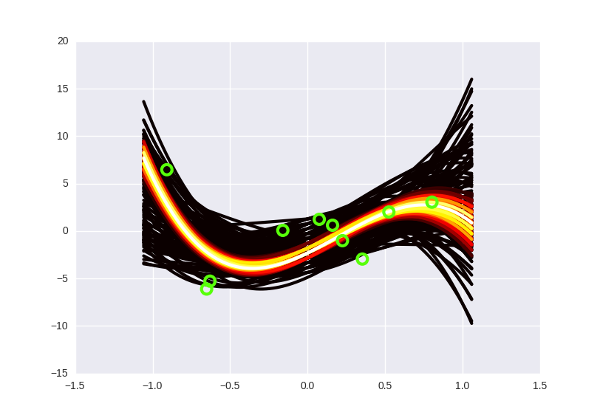
Заметьте, что более «горячие» кривые, конечно, имеют более высокую вероятность, но в Байесовской интерпретации это не означает, что эти кривые «правильные» (что мы должны взять их и выбросить все черные). Немного более интуитивный способ думать об этих кривых, по-моему — это представить, что вы смотрите как бы сверху на нормальное распределение, и видите, что в центре, конечно, есть какой-то пик вероятности, но сама по себе вероятность оказаться в точке пика все равно очень маленькая. Только собрав вместе какую-то часть распределения, можно «набрать» достаточно вероятности.
Переобучения не существует, Нео
Если вы все еще недоумеваете, зачем нам эта штука, то вот вам маленький бонус: байесовская регрессия неуязвима к переобучению (overfitting). Причем я не имею в виду просто «устойчива» или «надежна» как регрессия с регуляризацией — в определенной степени она к нему вообще неуязвима.
Что такое переобучение, еще раз? Это когда мы «слишком подгоняем» модель к имеющимся данным (например, подбираем такую кривую, которая идеально пройдет через все точки датасета, но покажет плохие предсказания на новых данных). В переводе на философский язык прошлой секции это означает, что когда мы искали «правильный» набор параметров, мы нашли какой-то ошибочный, неправильный. Это невозможно сделать с байесовским подходом, потому что там просто нет понятия «правильного» набора параметров! Странный черно-желтый конус на картинках выше говорит нам: «да, скорее всего, следующие точки будут где-то в середине вдоль белых кривых, но могут оказаться и с краю, и выше, и ниже, никаких проблем». Степень полинома можно увеличивать сколько угодно: вместе с ней будет расти число возможных кривых, а у каждой из них по отдельности будет падать вероятность. «Выживут» все равно только те, которые будут лежать близко к данным, в нашем оранжево-«горячем» пучке. Сделаем пятую степень? Да никаких проблем, Хьюстон:
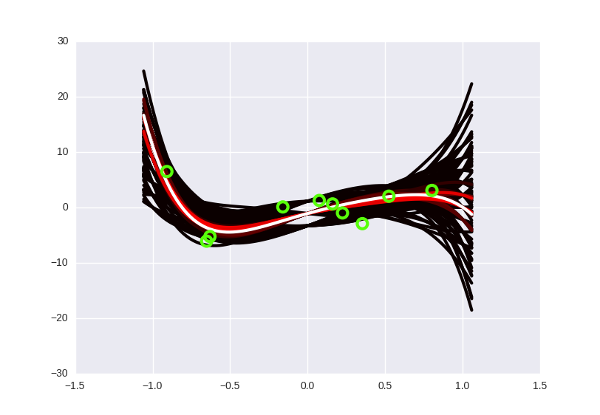
Выглядит чуть более блеклым, но это просто потому, что я уменьшил общее количество кривых — иначе мой лаптоп бы не проснулся.
На самом деле в таком контексте понятия переобучения вообще не существует. Невозможно неправильно найти параметр, потому что «параметр» — это не вещь, которую можно «найти», это здоровенное облако вероятности, которое становится «плотным» только там, где рядом лежат данные. Переобучения не существует, дамы и господа, расходимся. Не забудем сообщить всем этим важным ребятам из машинного обучения, что можно закрывать лавочку.
На всякий случай
Это не означает что байесовская регрессия всегда дает правильные предсказания и не может ошибаться — может, конечно. Допустим, следующая точка в датасете будет иметь x=3 и y=-20 и упадет гораздо ниже оранжевого пучка — тогда наша модель предскажет неправильное значение. Фокус в том, что обычную регрессию вам в этом месте понадобилось бы обучать с нуля и подправлять параметры, в то время как байесовскую нужно всего лишь «проапдейтить», положив новую точку в алгоритм — и пучок соответстветствующим образом изогнется.

Примерно вот так.
Кроме того, байесовская регрессия, как бы это, сказать, «инертная». Имея в наличии десяток точек вдоль белой кривой и один outlier, она, скорее всего, прогнется в его сторону немного, но не до конца. И это, вообще говоря, хорошо и правильно, потому что а вдруг это очередной результат шума?
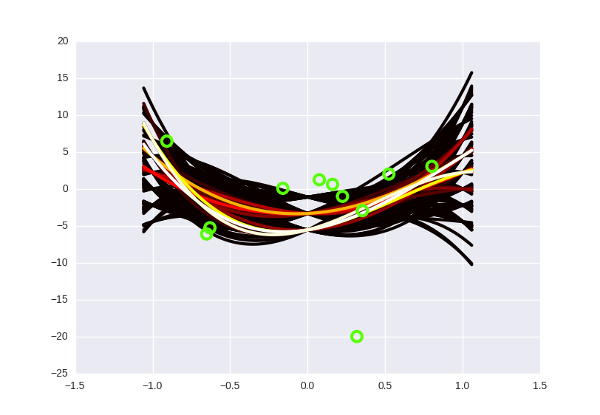
Примерно вот так.
Кроме того, байесовская регрессия, как бы это, сказать, «инертная». Имея в наличии десяток точек вдоль белой кривой и один outlier, она, скорее всего, прогнется в его сторону немного, но не до конца. И это, вообще говоря, хорошо и правильно, потому что а вдруг это очередной результат шума?
Почему ансамбли работают?
В машинном обучении есть такая очень простая техника — когда у вас есть несколько моделей и они все работают плохо, можно взять и усреднить (или еще как-нибудь объединить) их предсказания, и тогда они волшебным образом начинают работать хорошо. По-правильному это называется ансамбли, и их можно встретить почти где угодно, особенно на соревнованиях.
И вообще говоря, это не интуитивный вопрос: почему ансамбли вообще работают? В реальной жизни вещи редко ведут себя таким образом: если у вас есть десять плохих молотков, гвоздь не станет забиваться лучше от того, что вы будете использовать их по очереди. Иллюстрация к этому вопросу частично служит неплохой интуицией (по-моему) на тему того, почему работает байесовская регрессия. Выглядит это как-то так:
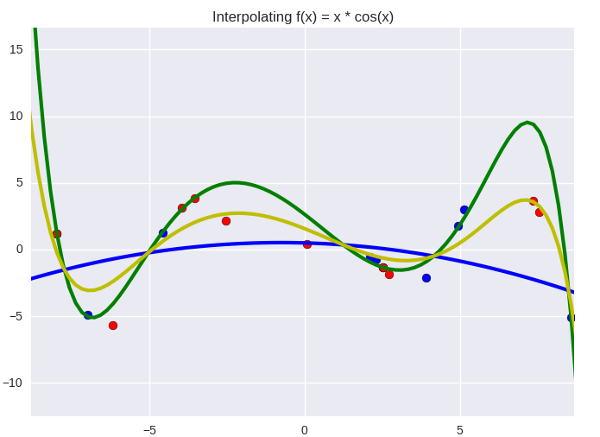
Зеленая линия — «сложная» модель (полином девятой степени), а синяя — «простая» (второй степени). Синией точки относятся к обучающей выборке, а красные — к тестовой. Желтая линия — простое среднее арифметическое между двумя моделями, и даже на глаз заметно, что она не такая размашистая, как зеленая, и действительно лежит ближе к красным точкам. Простота синего слегка компенсирует прыгучесть зеленого; средний вариант ближе к истине, чем оба отклонения, при условии, что отклонения направлены в разные стороны (это как раз одно из важных условий ансамблей — вам нужны разные модели для того, чтобы усреднение сработало).
Так вот, когда мы пытаемся предсказать что-то с байесовской регрессией, мы усредняем не две и не три модели, а — в нашем случае — два с половиной миллиона. Но погодите, на самом деле все еще круче. Это мы в своем кривом питонском коде ограничили коэффициенты значениями в -10 и 10 с шагом в 0.5, а если делать все по-правильному, они могут принимать любое значение на бесконечной числовой прямой. Секунду, включим калькулятор…
«Не-совсем-случайный бесконечнолес?»
От нейрона к множеству нейронов
Настало время немного разочароваться: способ, который мы придумали для расчета posterior, плохой и работает только для каких-то очень маленьких задач. Дело в том, что количество всех возможных сочетаний параметров, которые нужно перебрать, растет экспоненциально. Мы оценивали его как число значений параметра в степени числа параметров, и уже для полинома девятой степени (десять коэффициентов/параметров) нам в текущем сеттинге придется пробежаться по циклу 10485760000000000 раз.
А теперь настало время по-настоящему разочароваться: для более сложных моделей, то есть нейронных сетей (которые представляют собой просто несколько регрессионных юнитов, соединенных друг с другом), чистый байесовский метод становится еще более неприменимым. «Параметры» нейронной сети — это ее веса; а их в современных сетях может быть очень и очень много (миллионы штук с легкостью). Существуют всякие способы упростить этот процесс: например, случайным образом доставать значения posterior вместо того, чтобы рассчитывать его в каждой точки (это называется сэмплинг), но мы не зря их все проигнорировали — они недостаточно круты, чтобы помочь получить байесовскую нейронную сеть по-настоящему серьезных размеров.
На самом деле для каких-то отдельных моделей все еще хуже. Наши коэффициенты регрессии, грубо говоря, «ни от чего не зависели»; если мы хотим посмотреть, как ведет себя модель с таким-то набором параметров, мы можем просто взять его и подставить в формулу Байеса. В сетях распределение весов отдельного нейрона может зависеть от того, как ведет себя предыдущий нейрон, а тот, в свою очередь, зависит от предыдущего (а настоящее веселье начинается, когда зависимости замыкаются в цикл).
Собственно, это и есть главная причина, по которой лавочка не закрыта, люди продолжают бороться с переобучением
Что сделать, чтобы хоть что-нибудь работало
Мы можем немного отступить назад и удовлетвориться частичным решением проблемы: найти максимум байесовского пучка, самую близкую к центру и самую «горячую» кривую. Это будет не так круто, как знание пучка целиком, но все лучше, чем то, с чего мы начинали.
То есть мы ищем
Теперь смотрите: с
Подставляем вместо
Коэффициент перед экспонентой опять-таки не важен для поиска максимума (он не зависит от
Получается, что максимум достигается там, где сумма квадратов коэффициентов регрессии минимальна. Ничего не напоминает? Мы переизобрели регуляризацию, на минуточку, и получили отличное обоснование тому, зачем она вообще нужна (раньше это была какая-то технарско-инженерная штука, в духе «нуу, давайте просто заставим коэффициенты регрессии быть маленькими, чтобы она не прыгала туда-сюда», но с Байесом в ваш дом приходит просветление и все обретает смысл).
На статистическом жаргоне это называется maximum a posteriori или MAP-learning. В отличие от «чистого» Байеса, MAP отлично применяется и к нейронным сетям, и к чему угодно — под скромным именем «регуляризация». К сожалению, это не тру-байесовское решение, потому что в конце концов мы заканчиваем игру с каким-то штучным «набором параметров» — и поэтому такой подход тоже может страдать от переобучения, хотя и более устойчив к нему, чем метод максимального правдоподобия.
Маленький постскриптум
По мотивам дискуссии, начатой haqreu на тему того, православно ли пытаться объяснять математические вещи на пальцах, мне немного интересно общественное мнение на эту тему. Ткните куда-нибудь в опрос по результатам прочтения, если не затруднит?
Only registered users can participate in poll. Log in, please.
Как оно?
15.6%
Я уже знал все это, но мне скорее понравилось
120
0.91%
Я уже знал все это, и мне не понравилось
7
55.79%
Я не знал про байесовский подход, и этот текст сделал происходящее немного понятней
429
15.73%
Я не знал про байесовский подход, и так ничего и не понял отсюда
121
11.96%
Посмотреть результаты
92
769 users voted.
122 users abstained.