Люди встречаются, люди ссорятся, добавляются и удаляют друзей в социальных сетях. Этот пост о математике и алгоритмах, красивой теории, любви и ненависти в этом непостоянном мире. Этот пост о поиске компонент связности в динамических графах.

Большой мир генерирует большие данные. Вот и на нашу голову свалился большой граф. Настолько большой, что мы можем удержать в памяти его вершины, но не ребра. Кроме того, относительно графа приходят обновления – какое ребро добавить, какое удалить. Можно сказать, что каждое такое обновление мы видим в первый и последний раз. В таких условиях необходимо найти компоненты связности.

Поиск в глубину/ширину здесь не пройдут просто потому, что весь граф в памяти не удержать. Система непересекающихся множеств могла бы сильно помочь, если бы ребра в графе только добавлялись. Что же делать в общем случае?

Привет! На Хабре периодически появляются статьи, где авторы хотят вставить математические формулы: , или даже


У некоторых это получается, у некоторых — с трудом. parpalak сделал web-сервис для вставки svg формул, и это очень круто. Я хочу дополнить его небольшим скриптом, с которым вставка многих формул сведется к одной команде.

Небольшая предыстория. Этот пост я написал для двух целей. Во-первых, обкатать конвертор разметки Markdown + в хабрачитаемый вид. Во-вторых, рассказать об интересной задаче из data streaming. К концу написания, я обнаружил пост про LogLog четырехлетней давности. На мою удачу автор предыдущего поста делал упор на реализацию. Я же, полагаясь на , расскажу больше о математике.

Давайте представим, что у нас есть роутер. Через роутер проходит много пакетов по разным адресам. Нам интересно получить статистику, как много адресов задействовано в коммуникации. Есть пара проблем.

• Пакетов так много, что запомнить их все нельзя. Сказать ушедшему пакету «Вернись! Я все прощу,» — тоже.
• Всех возможных адресов . Столько памяти на роутере нет.

Задача. Есть последовательность целых чисел , все числа принимают значения от до . Требуется в один проход посчитать количество различных чисел, используя памяти.

Перед прочтением статьи рекомендую посмотреть посты про splay-деревья (1) и деревья по неявному ключу (2, 3, 4)

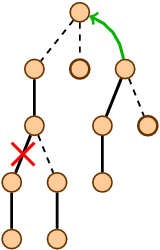Динамические деревья (link/cut trees) мало освещены в русскоязычном интернете. Я нашел только краткое описание на алголисте. Тем не менее эта структура данных очень интересна. Она находится на стыке двух областей: потоки и динамические графы.

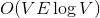В первом случае динамические деревья позволяют построить эффективные алгоритмы для задачи о поиске максимального потока. Улучшенные алгоритмы Диница и проталкивания предпотока работают за и 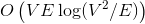соответственно. Если вы не знаете, что такое поток, и на лекциях у вас такого не было, спешите пополнить свои знания в Кормене.

Второй случай требует небольшого введения. Динамические графы — это активно развивающаяся современная область алгоритмов. Представьте, что у вас есть граф. В нем периодически происходят изменения: появляются и исчезают ребра, меняются их веса. Изменения нужно быстро обрабатывать, а еще уметь эффективно считать разные метрики, проверять связность, искать диаметр. Динамические деревья являются инструментом, который позволяет ловко манипулировать с частным случаем графов, деревьями.

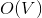Перед тем, как нырнуть под кат, попробуйте решить следующую задачу. Дан взвешенный граф в виде последовательности ребер. По последовательности можно пройти только один раз. Требуется посчитать минимальное покрывающее дерево, используя памяти и 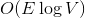времени. По прочтении статьи вы поймете, как легко и просто можно решить эту задачу, используя динамические деревья.

Сбалансированное дерево поиска является фундаментом для многих современных алгоритмов. На страницах книг по Computer Science вы найдете описания красно-черных, AVL-, B- и многих других сбалансированных деревьев. Но является ли перманентная сбалансированность тем Святым Граалем, за которым следует гоняться?

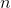Представим, что мы уже построили дерево на ключах и теперь нам нужно отвечать на запросы, лежит ли заданный ключ в дереве. Может так оказаться, что пользователя интересует в основном один ключ, и остальные он запрашивает только время от времени. Если ключ лежит далеко от корня, то 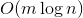запросов могут отнять времени. Здравый смысл подсказывает, что оценку можно оптимизировать до 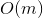, надстроив над деревом кэш. Но этот подход имеет некоторый недостаток гибкости и элегантности.

Сегодня я расскажу о splay-деревьях. Эти деревья не являются перманентно сбалансированными и на отдельных запросах могут работать даже линейное время. Однако, после каждого запроса они меняют свою структуру, что позволяет очень эффективно обрабатывать часто повторяющиеся запросы. Более того, амортизационная стоимость обработки одного запроса у них , что делает splay-деревья хорошей альтернативой для перманентно сбалансированных собратьев.

Привет, Хабр!

Сегодня мы поговорим об амортизационном анализе. Сначала я расскажу, что это такое, и приведу игрушечный пример. А потом расскажу, как его применить для анализа системы непересекающихся множеств.

Привет, Хабр!

При тестировании алгоритмов у меня часто возникает задача сгенерировать случайное бинарное дерево. Причем хотелка сводится не к абы какому случайному дереву, а взятому из равномерного распределения. Не смотря на кажущуюся простоту, эффективно построить такое дерево совсем нетривиально.

В названии этой статьи присутствуют слова «скобочная последовательность». За этими словами скрывается нечто большее, поскольку с помощью скобок можно описать очень разнообразные объекты, в том числе и бинарные деревья. На Хабре этому факту был посвящен отдельный пост.

В этой статье я расскажу несколько способов генерирования случайной скобочной последовательности, в том числе за линейное время, а потом приведу пример преобразования последовательности в бинарное дерево. Интересно?